intro to ml- regression & decision tree

Supervised Learning- Input

(𝑥 ⁽¹⁾ , 𝑦 ⁽¹⁾ ), …, (𝑥 ^(𝑚) , 𝑦 ^(𝑚) ) where 𝑥 ^(𝑖) is the ith data point and 𝑦 ^(𝑖) is the ith label associated to this data point.

Supervised Learning- Want

find a function f such that 𝑓(𝑥^(𝑖)) is a good approximation to 𝑦^(𝑖)

Supervised Learning- Goal

Use function f to predict unseen data points x

Supervised learning- X

attributes, predictor variables, or independent variables

Supervised Learning- Y

classes, target variable, or dependent variable

concept to be learned

hypothesis space

set of functions f:X→Y

Classification

• Learning how to separate/differentiate two or more classes (discrete or categorical target).

• Learning the separating boundary

Classification Examples

Fraud/Not-Fraud, Spam/Not-Spam, Sentiment Analysis, Image Classification (fruits, cars, etc.)

Regression

Learning how to predict a continuous numerical target

Regression Examples

predicting temperature or house/stock prices

Linear Regression- Input

(𝑥 ⁽¹⁾ , 𝑦 ⁽¹⁾ ), …, (𝑥 ^(𝑚) , 𝑦 ^(𝑚) ) where 𝑥 ^(𝑖) ∈ ℝ and 𝑦 ^(𝑖) ∈ ℝ.

Linear Regression- Hypothesis Space

set of linear functions 𝑓 𝑥 = 𝑎𝑥 + b, where 𝑎 ∈ ℝ and 𝑏 ∈ ℝ

Linear Regression- Goal

find a function f such that 𝑓 𝑋 ≈ Y, minimizing the error metric

Linear Regression- Error

computed based on the difference between predicted and actual values

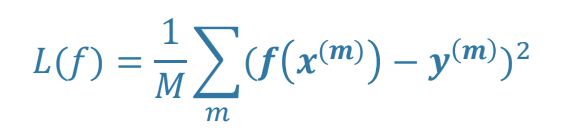
optimal linear hypothesis

minimizes squared differences between predicted value and actual value

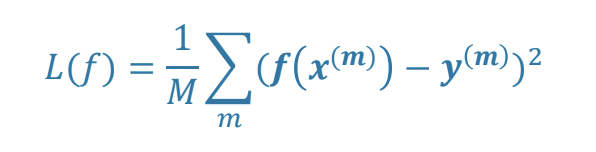
Gradient Descent

iteratively change parameter 𝜃 until reaching the minimum value for 𝐿(𝜃)

Gradient

derivative at point

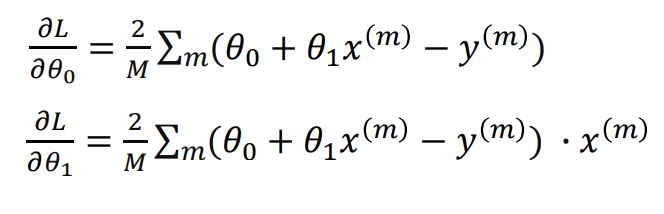
Gradient Descent Convergence

Gradient Descent will converge for convex functions, but the learning rate choice is crucial for that

Non-convex functions

can get stuck in a local minima

evaluate the learned hypothesis on

test data, not training data to avoid overfitting

Classification Input

(x⁽¹⁾, y⁽¹⁾),..., (x^(m), y^(m)) where x⁽ⁱ⁾∈ℝ and  y⁽ⁱ⁾∈ℤ

Classification

Want to learn a function f to predict a categorical or discrete target

What is decision tree?

It is a representation of concepts and hypothesis based on a set of Boolean/If-Then rules.The Boolean conditions will determine the outcomes.

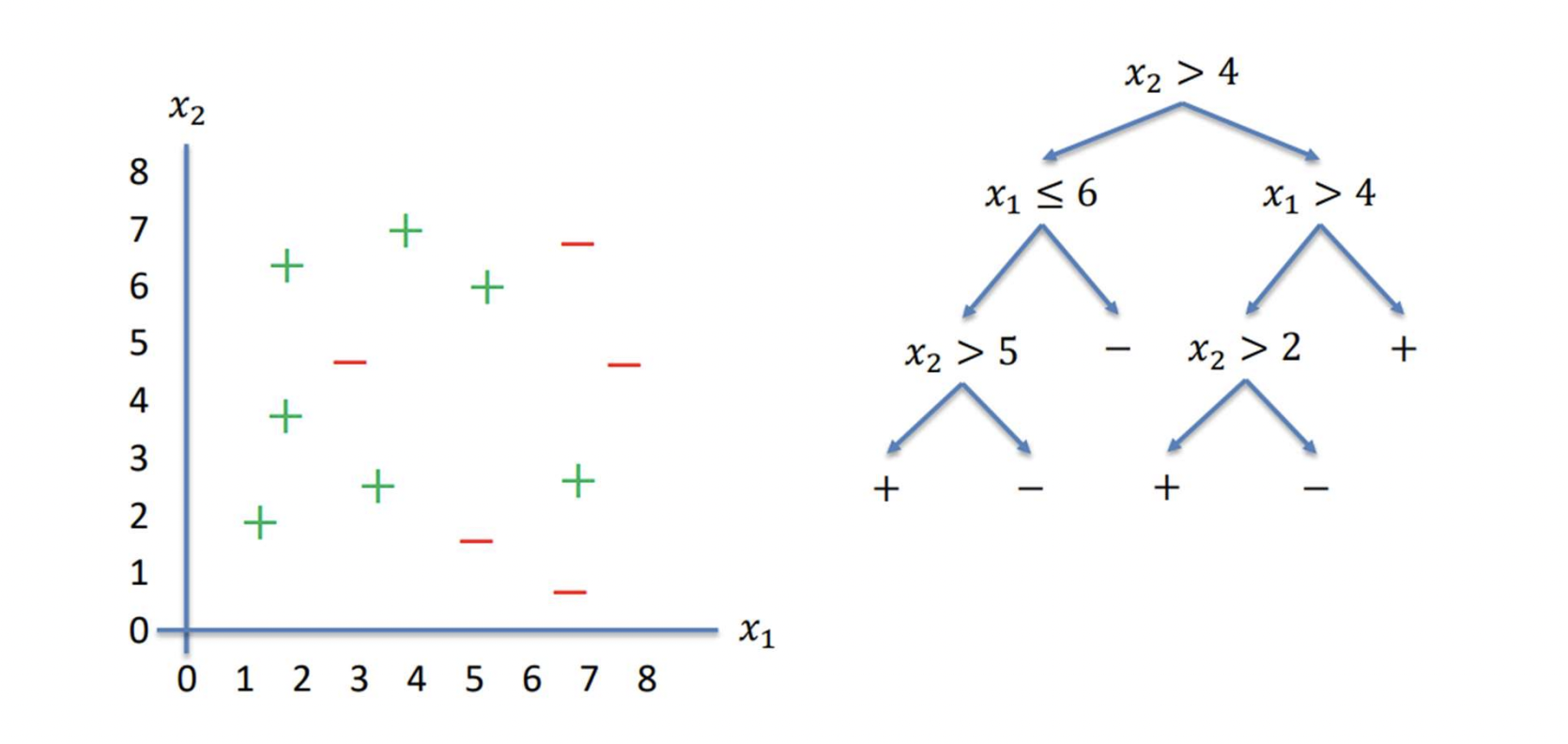
Example of Decision Tree

(Outlook=“Sunny”) AND (Humidity=“Normal”) → Yes (you should play tennis)but,

(Outlook=“Sunny”) AND (Humidity=“High”) → No (you shouldn’t play tennis)

internal (non-leaf) node

tests the value of a particular feature (Outlook, Humidity, Wind)

leaf node

specifies a class label / outcome (in this case whether or not you should play tennis)

DT’s classify instances..

by sorting them down the tree from the root to some leaf node, which provides the classification of the instance

Each node in the tree...

specifies a test of some attribute of the instance

Each branch descending from that node

corresponds to one of the possible values for this attribute

Classification process

An instance is classified by starting at the root of the tree, testing the attribute specified by this node, then moving down the tree branch corresponding to the value of the attribute in the given example. This process is then repeated for the subtree rooted at the new node

Induction Process

Inferring general rules from specific data

Deductive Process

Using general rules to reach specific conclusions

Decision trees divide

the feature space into axis parallel rectangles

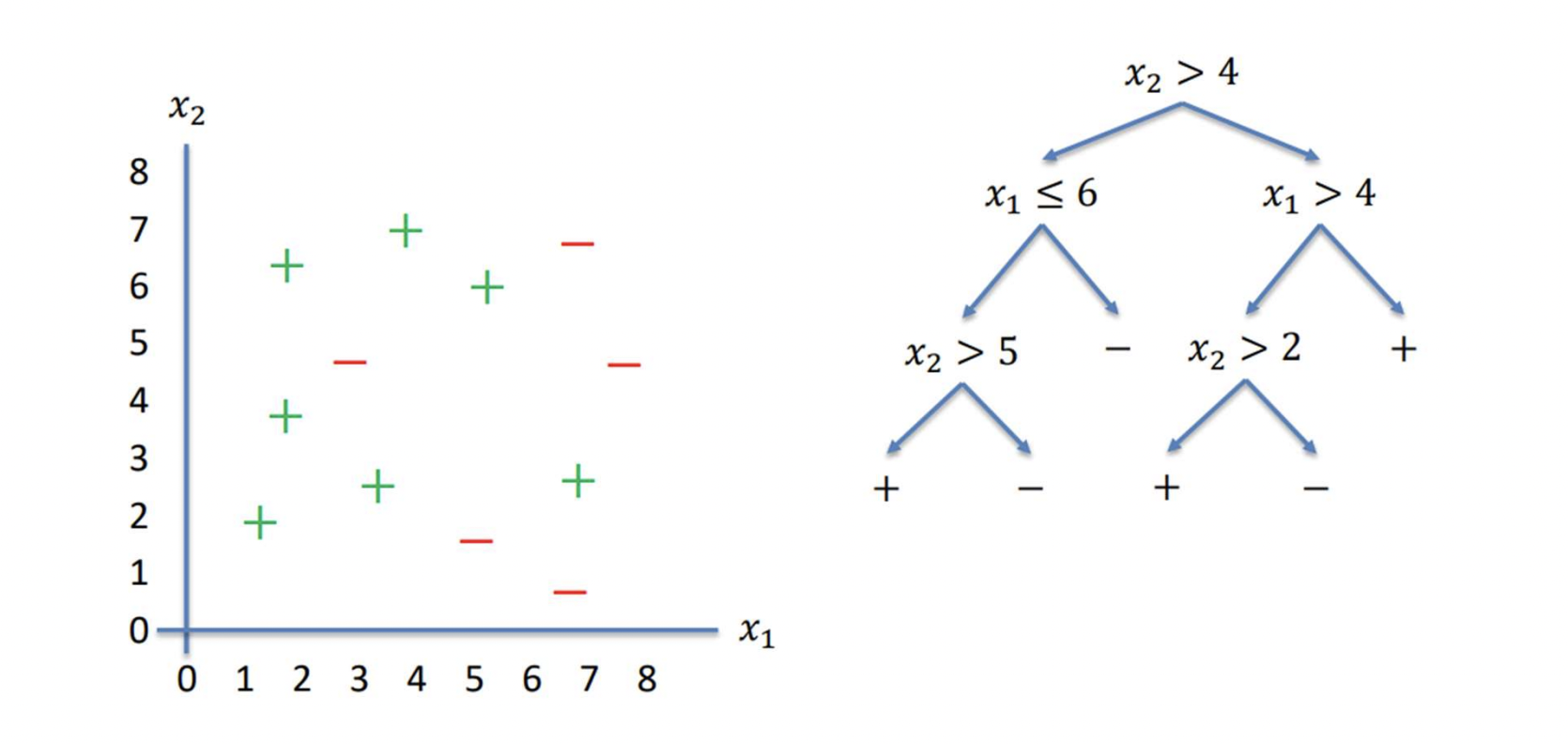
DT Algorithm

Recursive and Greedy Algorithm

Basic DT Algorithm

(i) Select an attribute

(ii) Split the data based on the values of this attribute (iii) Recurse over each new partition

How to decide which attribute?

Informally, we want that split that gives maximum purity at each node i.e., split such that all (or largest part of) instances belong to a single class

Entropy

• Entropy measures the degree of disorder, impurity or randomness in the system.

• It is equivalent to say that entropy measures the homogeneity of a decision tree node.

• Entropy is maximized for uniform distributions

• Entropy is minimized for distributions that place all their probability on a single outcome

for a binary random variable

Entropy is maximum at p=0.5, Entropy is zero at p=0 or p=1

Conditional Entropy

Conditional Entropy is the amount of information needed to quantify the random variable 𝑌given the random variable X. In practice, it tells you the uncertainty/impurity about a variable Y when another variable X is known

Information Gain

Informally, IG measures how good an attribute is for splitting heterogeneous group into homogeneous groups. Larger information gain corresponds to less uncertainty about 𝑌 given X

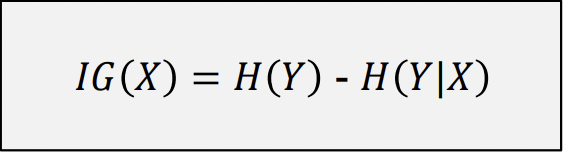
select an attribute..

with largest IG

Where to stop?

• When the node is pure

• When you run out of the attributes to recurse on

• When there is no more data points in the node (empty)

The class corresponding to a leaf is determined by majority vote

Discretization

form an ordinal categorical attribute.

• Equal interval bucketing

• Equal frequency bucketing (percentiles)

Binary Decision (𝑥𝑘< 𝑡 or 𝑥𝑘 ≥ 𝑡)

consider all possible splits and find the best threshold t

• More intensive computationally intensive, but do not need to test every threshold (just take the splits in between each consecutive pair of data points of same class)

• The learning algorithm maximizes over all attributes and all possible thresholds of the real-valued attributes

Handling training examples with missing attribute values

• Assign the most common values in the overall data

• Assign the most common value based on other examples with same target value

Overfitting

On small datasets some splits may perfectly fit to the training data, but they won’t generalize well on unseen/unknown datasets

Sources of Overfitting

Noise, Small number of examples in leaves

DT model should generalize well

it should work well on examples which you have not seen before

Train / Test Split

Use training part to learn the model.

Use test to evaluate performance and validate the model.

Pre-pruning or Early Stopping

Stop the algorithm (recursion) before it generates a fully grown tree, or before it reaches a base case (pure or empty node)

Criteria to early stopping

• Minimum number of samples in parents (before splitting)

• Minimum number of samples on leaf nodes

• Maximum depth of a tree

• Minimum IG

Post Pruning

Grow full tree, then remove branches or nodes to improve the model’s ability to generalize

Reduced error pruning

remove branches that do not affect the performance on test/validation data

greedily remove one that improves validation set accuracy

Minimum impurity decrease

remove nodes if the decrease in impurity is lower that a given threshold

Handling attributes with high cardinality (many values)

penalize the attribute A by incorporating a term called “Split Information”

Split Information

sensitive to how broadly and uniformly the attribute splits the data

where 𝑝(𝑋) = 𝑥 corresponds to the proportion of the data such that value x is assigned to attribute X.

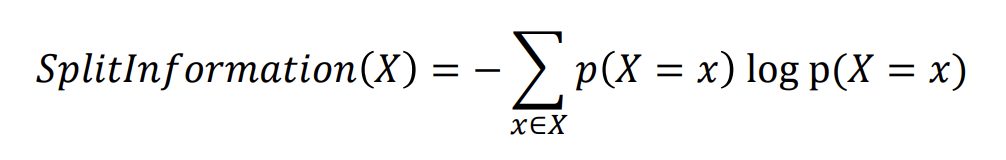
Gain Ratio

use instead of IG

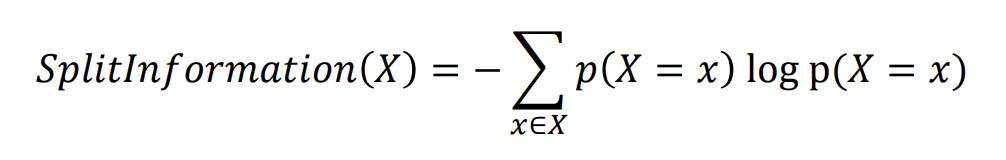
binary tree properties

• A complete binary tree of height h has 2_^h+1 -1 nodes

• Number of nodes at depth d is 2^d

Decision Tree Properties

• Due to the complexity inherent to decision tree structures, it usually overfits (pruning is always a good idea)

• Simple models that explain the data are usually preferred over more complicated ones

• Finding the small tree that explains the concept to be learned as good as a larger one is known to be an NP-hard problem

• Greedy heuristic: pick the best attribute (highest IG) at each stage

Common DT methods

ID3 (Iterative Dichotomiser 3)

CART (Classification And Regression Trees)

C4.5 (improvements over ID3)

CHAID (Chi Squared Automatic Interaction Detection)