22C Quiz 3 Chapter 25: A Binary Search Tree Implementation

1. The shape of a binary search tree affects the efficiency of the simple recursive search algorithm.

True or False?

True

The efficiency of the simple recursive search algorithm in a binary search tree (BST) is directly related to the shape of the tree. Ideally, the BST should be balanced, meaning that the height of the tree is minimized, so that the search operation has time complexity O(log n). However, if the BST is unbalanced and takes the form of a linked list (e.g., all nodes have only a right child or only a left child), the search operation could degrade to O(n) in the worst case, where "n" is the number of nodes in the tree.

2. You can create different binary search trees from the same data.

True or False?

True

You can create different binary search trees (BSTs) from the same set of data values. The structure of the BST depends on the order in which the values are inserted. For example, inserting the values in ascending or descending order will result in very different tree structures compared to a random insertion order. Different insertion sequences can lead to different tree shapes, and consequently, different levels of efficiency for various operations such as search, insertion, and deletion.

3. Binary search trees are not an efficient choice for searching if the data tends to remain stable.

True or False?

False

Binary search trees (BSTs) are generally efficient for searching, especially if they are balanced, regardless of whether the data remains stable or not. When the data is stable and the BST is balanced, searching, inserting, and deleting operations can be performed in \(O(\log n)\) time on average. However, if the BST becomes unbalanced (for example, if the data is inserted in sorted order without any rebalancing), the efficiency can degrade to \(O(n)\).

For stable data, certain self-balancing BSTs like AVL trees or Red-Black trees ensure that the tree remains balanced, thereby maintaining efficient search operations.

4. Searching a binary search tree is like performing a binary search of an array.

True or False?

True

Searching a binary search tree (BST) is conceptually similar to performing a binary search on a sorted array. In both cases, the search process involves narrowing down the search space by repeatedly comparing the target value to the current value and then deciding whether to continue searching in the left or right half (in the case of a sorted array) or the left or right subtree (in the case of a BST).

In a binary search of an array, you:

1. Start at the middle element.

2. Compare the target value to the middle element.

3. Depending on the comparison, move to either the left or right half of the array.

In a BST search, you:

1. Start at the root node.

2. Compare the target value to the value of the current node.

3. Depending on the comparison, move to either the left or right subtree.

The key difference is that in an array, elements are accessed by index, while in a BST, elements are accessed through pointers to nodes, and the tree's structure can affect the search efficiency (with balanced trees typically providing more consistent performance).

5. Every addition to a binary search tree adds a new root.

True or False?

False

In a binary search tree (BST), every addition (or insertion) of a new element does not add a new root. Instead, new elements are added as leaf nodes or internal nodes within the existing structure of the tree.

When you insert a new element into a BST:

1. You start at the root and compare the new element with the current node's value.

2. Depending on whether the new element is less than or greater than the current node's value, you move to the left or right subtree, respectively.

3. You continue this process until you find an appropriate empty spot (i.e., a null child), where you then insert the new element.

The root of the tree remains the same unless the tree was initially empty, in which case the first insertion does indeed establish the root. However, subsequent insertions do not change the root; they only extend the tree.

6. When adding an entry to a binary search tree, the search ends at a leaf if the entry is not already in the tree.

True or False?

True

When adding an entry to a binary search tree (BST), the search will end at a leaf node if the entry is not already in the tree. Here's a step-by-step outline of the process:

1. Start at the root of the tree.

2. Compare the entry to be inserted with the value of the current node.

- If the entry is less than the current node's value, move to the left child.

- If the entry is greater than the current node's value, move to the right child.

3. Repeat this process until you reach a node that does not have the relevant child (left for less than, right for greater than). This means you have found a leaf node or a terminal node where there's no further child to visit in the direction needed for the new entry.

At this point, you insert the new entry as a new child (either left or right) of this leaf node, thus preserving the BST property.

7. For best performance, when you add entries to a binary search tree, you should add them in sorted order.

True or False?

False

Adding entries to a binary search tree (BST) in sorted order results in a highly unbalanced tree, specifically a degenerate tree or a "linked list" configuration. In this scenario, every node only has one child, and the height of the tree becomes \(O(n)\) where \(n\) is the number of nodes. As a result, operations such as insertion, deletion, and search will have \(O(n)\) time complexity instead of the optimal \(O(\log n)\) expected for a balanced binary search tree.

For best performance, entries should be added in a random or balanced manner. Techniques such as self-balancing binary search trees (e.g., AVL trees, Red-Black trees) or creating a balanced tree from a sorted list (e.g., dividing the list in half repeatedly) can help maintain the balanced nature of the tree, ensuring logarithmic time complexity for operations.

8. You can implement the ADT dictionary using a binary search tree.

True or False?

True.

You can implement the Abstract Data Type (ADT) dictionary using a binary search tree (BST). In a dictionary, you store key-value pairs and typically provide operations such as insertion, deletion, and search. A BST is well-suited for this purpose because it allows efficient lookup, insertion, and deletion operations, all of which are required for a dictionary.

When using a BST for a dictionary:

- Keys are stored in the nodes, and the value associated with each key is also stored alongside the key within the node.

- The BST provides efficient \(O(\log n)\) time complexity for these operations as long as the tree remains balanced.

For even better performance and to ensure the tree remains balanced, self-balancing BST variants like AVL trees or Red-Black trees are often used. These maintain \(O(\log n)\) time complexity for insertion, deletion, and search operations, regardless of the order of entry insertion.

1. Why can't the two setTree methods that are inherited from BinaryTree be used in the class BinrarySearchTree?

-One could create a tree that does not have the properties of a binary search tree

In the context of implementing a Binary Search Tree (BST), the two methods `setTree` inherited from the `BinaryTree` class typically can't be used directly because they might not enforce the BST property. The BST property requires that for any given node `N`:

- All values in the left subtree of `N` are less than the value of `N`.

- All values in the right subtree of `N` are greater than the value of `N`.

If the `setTree` methods allow setting the entire tree or its subtrees without checking and maintaining this property, they could generate a tree that does not adhere to the rules of a BST. Consequently, the search operations for which BSTs are optimized (`O(log n)` time complexity for balanced trees) could become inefficient.

In summary, the inherited `setTree` methods might not incorporate the necessary logic to maintain the ordered structure required by BSTs and could thus violate its fundamental properties.

2. How does the class BinarySearchTree handle the two setTree methods that are inherited from BinaryTree?

-They are overridden with methods that throw an exception if called

Here is an example in pseudocode of how this could be handled:

```java

class BinarySearchTree extends BinaryTree {

@Override

public void setTree(TreeNode newRoot) {

if (isValidBST(newRoot)) {

super.setTree(newRoot);

} else {

throw new IllegalArgumentException("The provided tree does not maintain BST properties.");

}

}

@Override

public void setTree(Object data, BinaryNode left, BinaryNode right) {

if (isValidBSTData(data, left, right)) {

super.setTree(data, left, right);

} else {

throw new IllegalArgumentException("The provided subtrees do not maintain BST properties.");

}

}

private boolean isValidBST(TreeNode node) {

// Implement validation logic to check if the entire tree maintains BST properties.

// Example: Check if all nodes in left subtree are less than node,

// and all nodes in right subtree are greater than node.

}

private boolean isValidBSTData(Object data, BinaryNode left, BinaryNode right) {

// Implement validation logic for the provided node data and its subtrees.

// Example: Check if data is greater than all values in left subtree and

// less than all values in right subtree.

}

}

```

3. Write a pseudo code algorithm for searching a binary search tree.

If(binary search tree is empty)

return false

else if(object being searched for is equal to the root of the tree)

return true

else if(object being searched for is less than the root of the tree)

recursively call the search algorithm on the left subtree

else

recursively call the search algorithm on the right subtree.

or

```plaintext

FUNCTION searchBST(node, targetValue):

// Base case: if the node is null

IF node IS NULL THEN

RETURN NULL // target not found

// Base case: if the node's value is equal to the target value

IF node.value == targetValue THEN

RETURN node // target found

// Recursive case: if the target value is less than the node's value

IF targetValue < node.value THEN

RETURN searchBST(node.left, targetValue) // search in the left subtree

ELSE

// Recursive case: if the target value is greater than the node's value

RETURN searchBST(node.right, targetValue) // search in the right subtree

END IF

END FUNCTION

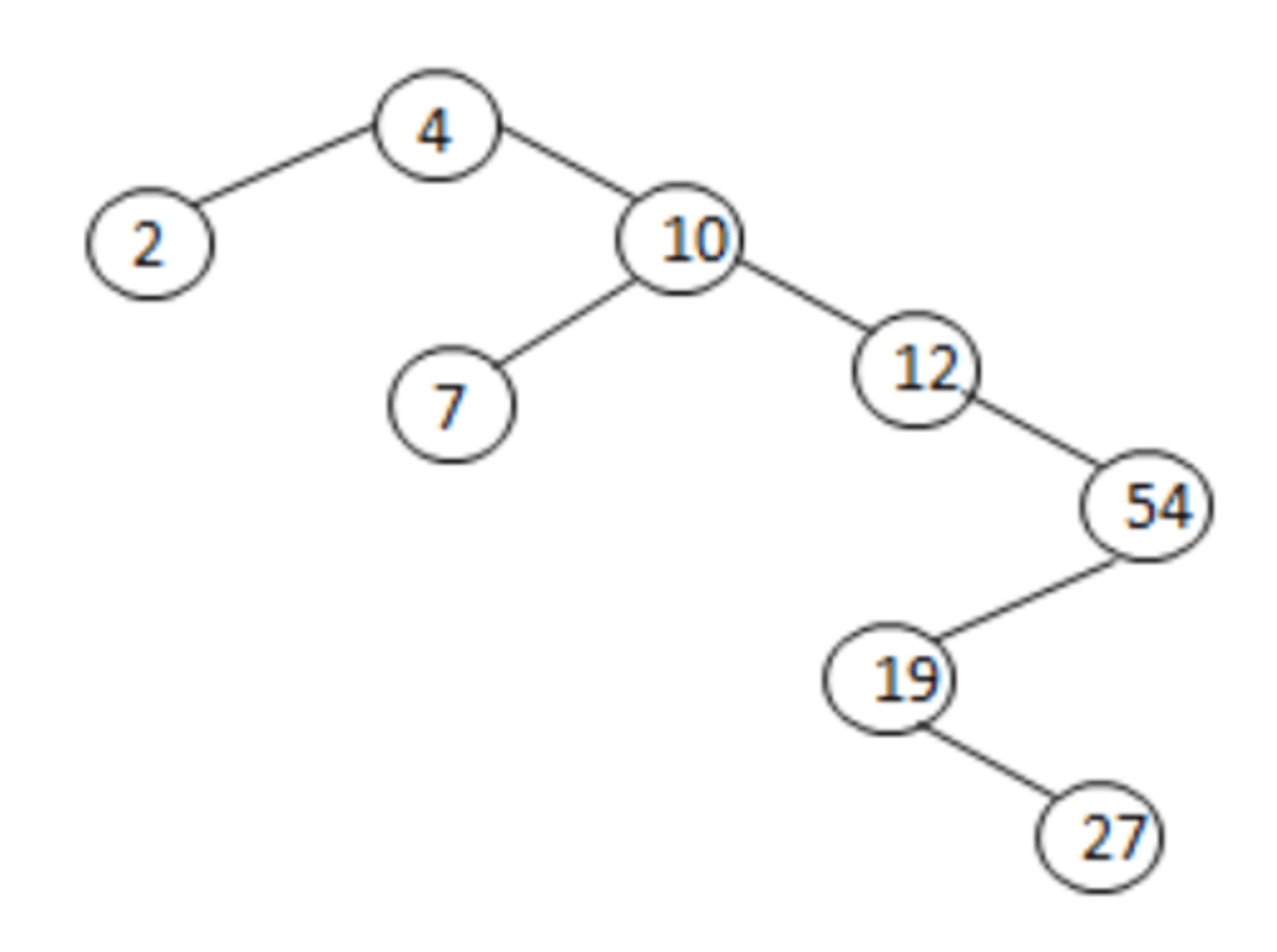
4. Draw the binary search tree from the following input.

4, 10, 12, 54, 19, 27, 7, 2

To draw a binary search tree (BST) from the given input values, we insert each value sequentially following the binary search tree property. The property dictates that each left child is less than its parent node, and each right child is greater than its parent node.

Given the input:

4, 10, 12, 54, 19, 27, 7, 2

1. *Insert 4:*

- 4 is the root node.

```

(4)

```

2. *Insert 10:*

- 10 is greater than 4, so it goes to the right of 4.

```

---(4)

-----\

-----(10)

```

3. *Insert 12:*

- 12 is greater than 4 and also greater than 10, so it goes to the right of 10.

```

---(4)

-----\

-----(10)

--------\

--------(12)

```

4. *Insert 54:*

- 54 is greater than 4, 10, and 12, so it goes to the right of 12.

```

---(4)

-----\

-----(10)

--------\

--------(12)

-----------\

-----------(54)

```

5. *Insert 19:*

- 19 is greater than 4 and 10, but less than 12, so it goes to the left of 54.

```

---(4)

-----\

-----(10)

--------\

--------(12)

-----------\

-----------(54)

-----------/

--------(19)

```

6. *Insert 27:*

- 27 is greater than 4, 10, and 12, but less than 54 and greater than 19, so it goes to the right of 19.

```

---(4)

-----\

-----(10)

--------\

--------(12)

-----------\

-----------(54)

-----------/

--------(19)

-----------\

-----------(27)

```

7. *Insert 7:*

- 7 is greater than 4 but less than 10, so it goes to the left of 10.

```

--(4)

----\

----(10)

----/--\

--(7)---(12)

----------\

----------(54)

----------/

-------(19)

----------\

----------(27)

```

8. *Insert 2:*

- 2 is less than 4, so it goes to the left of 4.

```

---(4)

--/--\

(2)---(10)

------/--\

----(7)--(12)

------------\

------------(54)

------------/

----------(19)

------------\

------------(27)

```

So, the final binary search tree looks like this:

```

---(4)

--/--\

(2)---(10)

------/--\

----(7)--(12)

------------\

------------(54)

------------/

5. Given the following binary search tree, draw the tree after adding 3.

(See answer side for Diagram)

Let's outline the structure and the process to add the value 3 to the given binary search tree (BST). The current structure of the BST is:

```

--------(4)

--------/-\

-----(2)--(10)

----------/-\

-------(7)---(12)

---------------\

---------------(54)

----------------/

-------------(19)

----------------\

----------------(27)

```

To insert the value 3, we follow these steps according to the properties of a BST (values to the left are smaller and values to the right are larger):

1. Start at the root (4).

2. Since 3 is less than 4, move to the left subtree rooted at 2.

3. 3 is greater than 2, so we add 3 as the right child of 2.

After adding 3, the updated BST is:

```

---------(4)

--------/----\

-----(2)------(10)

--------\------/--\

--------(3)--(7)--(12)

---------------------\

---------------------(54)

---------------------/

-------------------(19)

----------------------\

----------------------(27)

```

This final representation maintains the properties of a BST after adding the value 3.

6. Given the following binary search tree, draw the tree after adding 9.

(See answer side for Diagram)

Insertion in binary search tree:

Step 1: The only rule to follow while insertion is that

left < root < right,

the left subtree should be less than the root node and the right subtree should be greater than the root node.

Step 2: Compare 9 with the root node, as 9 is greater than the root node (4) so move to the right child of 4.

Step 3: Again check 9 with 10, 10 > 9 therefore move to the left child of 10.

Step 4: Now, 7 < 9 traverse to the right child, since 7 has no right child so 9 will be inserted as the right child.

The binary search tree after inserting 9 is shown below:

---(4)

---/-\

(2)--(10)

-----/-\

--(7)---(12)

----\-----\

----(9)----(54)

-----------/

--------(19)

-----------\

-----------(27)

Explanation:

Continually move to the right or left subtree, depending on the rule, and insert the new node there when we reach a position where either the left or right subtree is null.

7. How do you remove a node that is a leaf in a binary search tree?

You locate the parent node and set the appropriate child reference in the parent node to null to remove a leaf node in the binary tree.

8. When you add entries to a binary search tree, if possible, you should not add them in sorted order.

Explain.

Adding them in sorted, or nearly sorted order produces a tree with a very large height yielding an O(n) performance on the add, remove and getEntry operations. if the data is entered in a ore random fashion, the height will be smaller, approaching the optimum performance of O(log n) for a full search tree.

or

When you add entries to a binary search tree (BST), you should avoid adding them in sorted order because this can result in an unbalanced tree with poor performance. Here are the key reasons why:

1. **Degenerate Tree**: If entries are added in sorted order (either ascending or descending), the BST can degenerate into a linear structure that resembles a linked list. In this case, each node has only one child, resulting in a tree with a height equal to the number of nodes (n).

2. **Increased Time Complexity**: A degenerate tree has poor efficiency, leading to operations such as insertion, deletion, and search taking O(n) time complexity instead of the optimal O(log n) obtained with a balanced BST. This significantly degrades the performance, especially for large datasets.

3. **Reduced Efficiency of Operations**: The purpose of a BST is to provide efficient lookup, insertion, and deletion operations. When the tree is balanced, these operations take logarithmic time. However, with a degenerate tree, the operations become as slow as traversing a linked list.

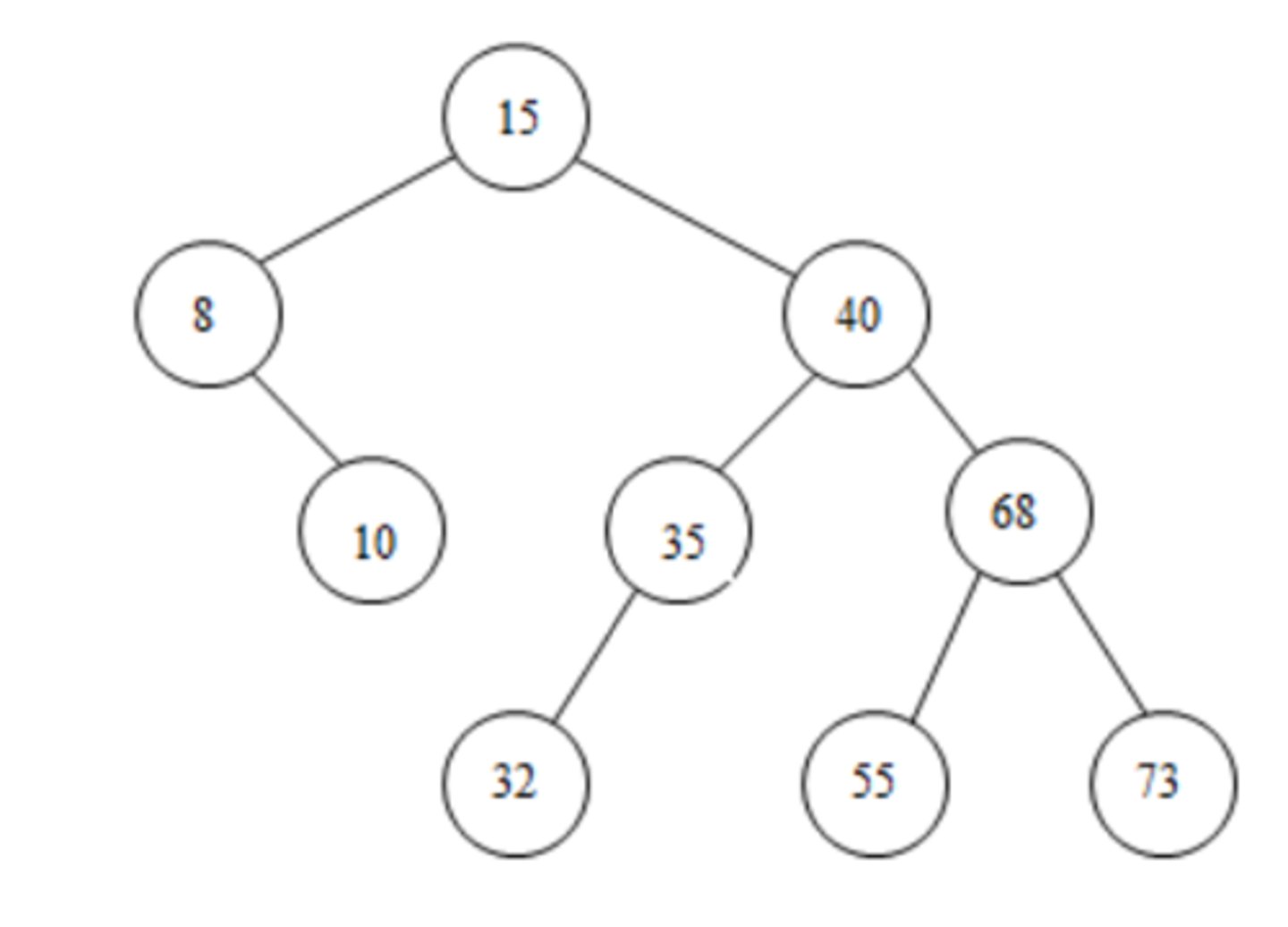
9. Given the following binary search tree, draw the tree after deleting the node with the value 55.

(See answer side for Diagram)

Original

---------(15)

--------/----\

-----(8)------(40)

-------\------/---\

-------(10)--(35)-(68)

-------------/-----/-\

-----------(32)-(55)-(73)

Since node 55 is a leaf node, simply delete it

After deleting node 55:

---------(15)

--------/----\

-----(8)------(40)

-------\------/---\

-------(10)-(35)-(68)

------------/------\

----------(32)-----(73)

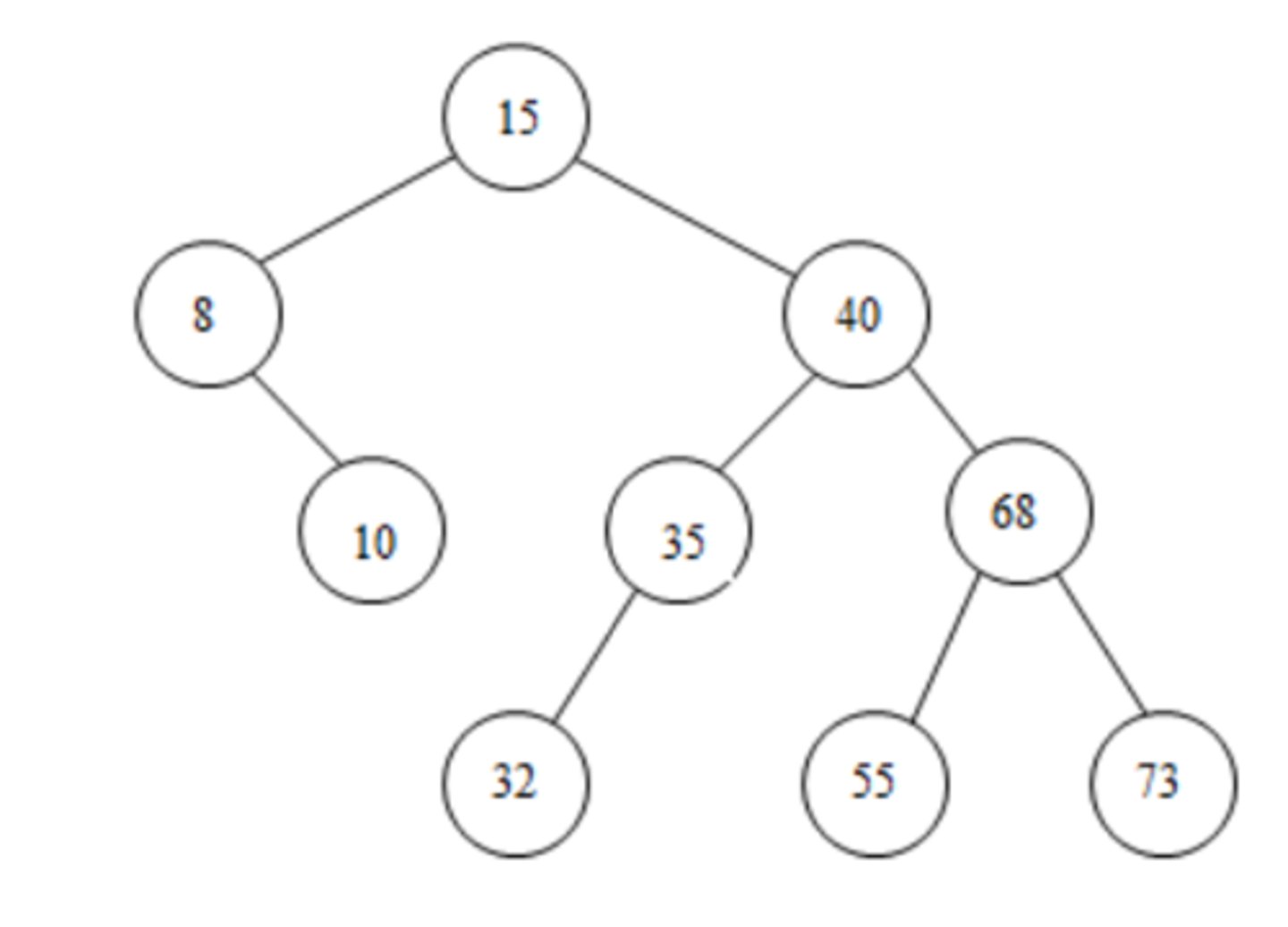
10. Given the following binary search tree, draw the tree after deleting the node with the value 32.

(See answer side for Diagram)

Original

---------(15)

--------/----\

-----(8)------(40)

-------\------/---\

-------(10)--(35)-(68)

-------------/-----/-\

-----------(32)-(55)-(73)

Since node 32 is a leaf node, simply delete it

After deleting node 32:

---------(15)

--------/----\

-----(8)------(40)

-------\------/---\

-------(10)--(35)-(68)

-------------------/-\

----------------(55)-(73)

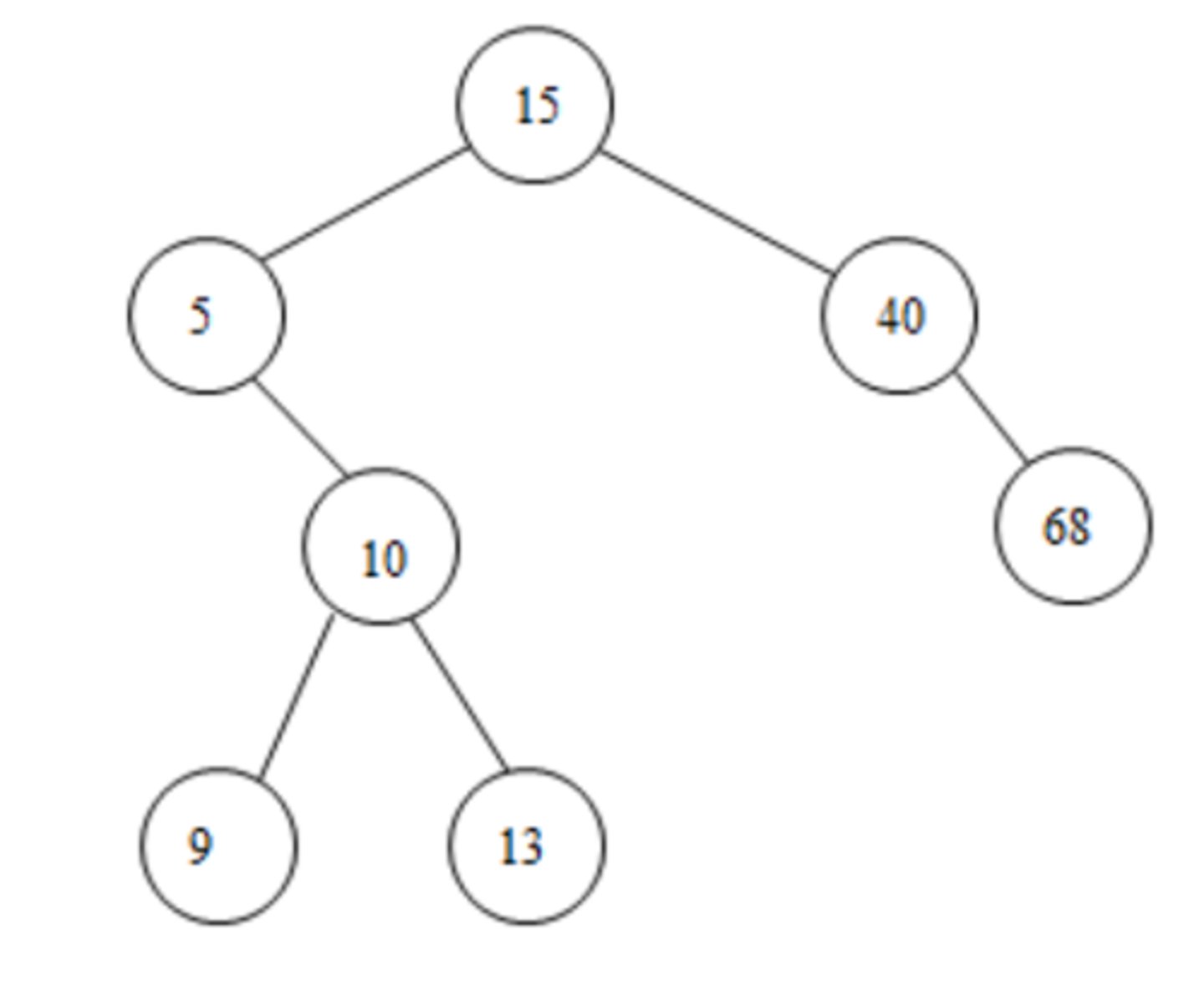
11. Given the following binary search tree, draw the tree after deleting the node with the value 10.

(See answer side for Diagram)

Original:

---------(15)

--------/----\

-----(5)------(40)

-------\---------\

-------(10)------(68)

--------/-\

------(9)-(13)

In a binary search tree, all the elements which are less than root or parent node is placed to it's left while all the elements which are more than the root is placed to it's right.

Here when we delete node 10, it can be placed either with minimum value of its left child or with maximum value of its right child.

Thus here node 10 can be replaced with node 9 or node 13. In both cases, its property will be maintained.

After deleting node 10:

---------(15)

--------/----\

-----(5)------(40)

-----/----------\

---(13)----------(68)

-----\

-----(9)

or

---------(15)

--------/----\

-----(5)------(40)

-------\--------\

-------(9)-----(68)

-------/

----(13)

1. The data in a node's _____ subtree are less than the data in a node's _____ subtree.

a. left, right

b. right, left

c. left, middle

d. middle, right

a. left, right

In a binary search tree (BST), the data in each node is organized such that:

- The data in the left subtree of a node are less than the data in the node itself.

- The data in the right subtree of a node are greater than the data in the node itself.

This arrangement ensures that the binary search tree property is maintained and allows for efficient searching, insertion, and deletion operations.

2. In the interface SearchTreeInterface, what does the method getEntry return if the object being sought doesn't exist?

a. null

b. false

c. 0

d. throws an exception

a. null

In an interface for a search tree, such as `SearchTreeInterface`, the method `getEntry` typically returns `null` if the object being sought doesn't exist. This is a common design choice to signify the absence of the element being searched for.

3. In the interface SearchTreeInterface, what does the method remove return if the object being sought doesn't exist?

a. null

b. false

c. 0

d. throws an exception

a. null

In a typical implementation of a search tree interface, the `remove` method would return `null` if the object being sought for removal doesn't exist. This convention indicates that no element was found to remove.

4. In the interface SearchTreeInterface, what does the method add return if the object being added doesn't exist?

a. null

b. false

c. 0

d. throws an exception

a. null

5. In the interface SearchTreeInterface, what does the method add return if the object being added already exists in the tree?

a. the existing entry that matched the parameter

b. true

c. 1

d. throws an exception

a. the existing entry that matched the parameter

This option means that if the object being added already exists in the tree, the method will return the existing entry without adding a new duplicate. This is the most logical choice as it follows the typical behavior of ensuring uniqueness in data structures like search trees.

6. In the interface SearchTreeInterface, the method getEntry returns an object in the tree that matches the given entry according to the entry's _____ method.

a. compareTo

b. equalTo

c. equals

d. same

a. compareTo

The `compareTo` method is specifically used to compare two objects to determine their ordering with respect to each other, returning a negative integer, zero, or a positive integer if the object is less than, equal to, or greater than the specified object, respectively. This is crucial for operations like insertion, deletion, and searching in the context of data structures such as binary search trees, where ordering is key.

7. In a binary search tree, the getInorderIterator inherited from the class BinaryTree sorts data

a. in ascending order

b. in descending order

c. in striped order

d. none of the above

a. in ascending order

In a binary search tree, the `getInorderIterator` method you referred to performs an inorder traversal. Here is how it typically works:

When you perform an *inorder traversal* on a binary search tree:

- You first visit the left subtree.

- Then you visit the root node.

- Finally, you visit the right subtree.

This traversal order naturally processes the nodes in *ascending sorted order* because, in a binary search tree, all nodes in the left subtree of a node are less than the node, and all nodes in the right subtree are greater than the node.

8. Every addition to a binary search tree adds a new

a. leaf

b. parent

c. ancestor

d. root

a. leaf

n a binary search tree (BST), every new addition (insertion) of a node follows these steps:

1. The new node is compared with existing nodes starting from the root.

2. Based on comparisons, it descends left or right until it finds an appropriate position where there is no existing node (i.e., it finds a null, or empty, spot).

3. It is then added as a leaf node in this empty spot.

9. If a node x is the inorder predecessor of node y then node x must appear in y's _____ subtree.

a. left

b. right

c. middle

d. all of the above

a. left

When we talk about the inorder predecessor of a node \( y \) in a binary search tree (BST), the predecessor appears in a specific relationship depending on the structure of the tree and this node's position.

- If node \( y \) has a left subtree, the inorder predecessor of

\( y \) is the largest node (the rightmost node) in the left subtree of \( y \).

- If node \( y \) does not have a left subtree, the inorder predecessor is one of \( y \)'s ancestors, specifically the highest ancestor of \( y \) whose right child is also an ancestor of \( y \).

Given these typical scenarios for identifying the inorder predecessor, you should notice that it must involve navigation through the left subtree of the node \( y \).

10. If a node x is the inorder successor of node y then node x must appear in y's _____ subtree.

a. right

b. left

c. middle

d. all of the above

a. right

In a binary search tree (BST), the inorder successor of a node \( y \) is defined as the node that comes immediately after \( y \) in the inorder traversal of the BST. For a given node \( y \):

- If node \( y \) has a right subtree, its inorder successor is the smallest node in that right subtree (i.e., the leftmost node in the right subtree).

- If node \( y \) does not have a right subtree, the inorder successor is one of \( y \)'s ancestors, specifically the lowest ancestor of \( y \) whose left child is also an ancestor of \( y \).

Given that we are usually referring to the most common scenario:

- When node \( y \) has a right subtree, the inorder successor \( x \) will appear in \( y \)'s right subtree.

11. The inorder predecessor of a node N is

a. the largest entry in N's left subtree

b. the largest entry in N's right subtree

c. the smallest entry in N's left subtree

d. the smallest entry in N's right subtree

a. the largest entry in N's left subtree

The inorder predecessor of a node \( N \) in a binary search tree (BST) is the node that comes just before \( N \) in an inorder traversal (which visits nodes in ascending order).

To find the inorder predecessor specifically:

- If \( N \) has a left subtree, the inorder predecessor is the largest node in the left subtree.

12. The inorder successor of a node N is

a. the smallest entry in N's right subtree

b. the smallest entry in N's left subtree

c. the largest entry in N's right subtree

d. the largest entry in N's left subtree

a. the smallest entry in N's right subtree

The inorder successor of a node \( N \) in a binary search tree (BST) is the node that comes just after \( N \) in an inorder traversal (which visits nodes in ascending order).

To find the inorder successor specifically:

- If \( N \) has a right subtree, the inorder successor is the smallest node in the right subtree.

13. The largest entry in a node N's left subtree is

a. the subtree's rightmost node

b. the subtree's leftmost node

c. the left child of N

d. the right child of N

a. the subtree's rightmost node

To find the largest entry in a node \( N \)'s left subtree in a binary search tree (BST), you need to traverse to the rightmost node in that left subtree (since the rightmost node will have the highest value).

14. The largest entry in a node N's right subtree is

a. the subtree's rightmost node

b. the subtree's leftmost node

c. the left child of N

d. the right child of N

a. the subtree's rightmost node

To find the largest entry in a node \( N \)'s right subtree in a binary search tree (BST), you need to find the rightmost node in that right subtree (since the rightmost node will have the highest value).

15. The smallest entry in a node N's left subtree is

a. the subtree's leftmost node

b. the subtree's rightmost node

c. the left child of N

d. the right child of N

a. the subtree's leftmost node

To find the smallest entry in a node \( N \)'s left subtree in a binary search tree (BST), you need to find the leftmost node in that left subtree (since the leftmost node will have the smallest value).

16. The smallest entry in a node N's right subtree is

a. the subtree's leftmost node

b. the subtree's rightmost node

c. the left child of N

d. the right child of N

a. the subtree's leftmost node

In a binary search tree (BST), to find the smallest entry in a node \( N \)'s right subtree, you need to find the leftmost node in that right subtree (since the leftmost node will have the smallest value).

17. When adding an entry to a binary search tree, when does the search ends?

a. when the item is found

b. at a leaf if the entry is not already in the tree

c. both a & b

d. none of the above

c. both a & b

When adding an entry to a binary search tree, the search ends under the following conditions:

1. If the entry already exists in the tree, the search ends when the item is found.

2. If the entry does not exist in the tree, the search ends when it reaches a leaf node where the entry should be inserted.

18. Given a binary search tree with n nodes and height h, what is the maximum number of comparisons that each operation requires for the method add?

a. O(h)

b. O(n)

c. O(log h)

d. O(1)

a. O(h)

For a binary search tree, the time complexity of the add (or insert) operation is primarily dependent on the height (h) of the tree. In the worst-case scenario (which occurs when the tree is unbalanced and resembles a linked list), the height can be equal to the number of nodes (n), so the number of comparisons can be as many as n.

However, typically the number of comparisons required to find the correct insertion point in a balanced tree is proportional to the height of the tree.

19. Given a binary search tree with n nodes and height h, what is the maximum number of comparisons that each operation requires for the method remove?

a. O(h)

b. O(n)

c. O(log h)

d. O(1)

a. O(h)

For the remove operation in a binary search tree, much like the add operation, the time complexity is primarily dependent on the height (h) of the tree. In the worst-case scenario, you might need to traverse from the root to a leaf, which would take O(h) comparisons. Additionally, removing a node might require finding the inorder predecessor or successor, which shall also involve traversals, but still tied to the height of the tree.

20. Given a binary search tree with n nodes and height h, what is the maximum number of comparisons that each operation requires for the method getEntry?

a. O(h)

b. O(n)

c. O(log h)

d. O(1)

a. O(h)

For the getEntry operation in a binary search tree, you need to search from the root to potentially a leaf node to find a specific entry. The depth of the search is dependent on the height (h) of the tree. Therefore, in the worst case, you might have to make O(h) comparisons to find the desired entry.

21. The maximum possible height of a binary search tree with n nodes is

a. n

b. log n

c. n²

d. n-2

a. n

The height of a binary search tree (BST) depends on how the nodes are inserted. The maximum possible height occurs when the BST is essentially a linked list, which happens when each node has only one child. In this scenario, the height is equal to the number of nodes minus one.

22. What is the worst-case performance of the add method in a binary search tree with linked nodes?

a. O(n)

b. O(1)

c. O(log n)

d. O(n²)

a. O(n)

In the worst case, a binary search tree (BST) becomes essentially a linked list if the nodes are inserted in a sorted order. In this scenario, the add (or insert) operation would have to potentially traverse all \( n \) nodes to find the correct position for the new node.

23. What is the worst-case performance of the remove method in a binary search tree with linked nodes?

a. O(n)

b. O(1)

c. O(log n)

d. O(n²)

a. O(n)

In a binary search tree (BST) that has degenerated into a linked list (which can happen in the worst-case scenario with certain sequences of insertions), removing a node may require traversing through all \( n \) nodes.

24. What is the worst-case performance of the getEntry method in a binary search tree with linked nodes?

a. O(n)

b. O(1)

c. O(log n)

d. O(n²)

a. O(n)

The `getEntry` method in a binary search tree (BST) involves searching for a node that matches a given entry. In the worst-case scenario, where the BST has degenerated into a linked list, you may have to traverse through all \( n \) nodes to find the entry.

25. What is the worst-case performance of the add method in a full binary search tree with linked nodes?

a. O(log n)

b. O(n)

c. O(1)

d. O(n²)

a. O(log n)

\( O(\log n) \), could be correct if the binary search tree is well-balanced, such as in the case of a self-balancing binary search tree (e.g., AVL tree, Red-Black tree). In a balanced binary search tree, the height of the tree is minimized to \( \log n \), ensuring that the `add` (or insert) operation typically involves traversing a height of \( \log n \) levels to find the appropriate insertion point.

26. What is the worst-case performance of the remove method in a full binary search tree with linked nodes?

a. O(log n)

b. O(n)

c. O(1)

d. O(n²)

a. O(log n)

\(O(\log n)\): This could be correct if the BST is balanced. In a balanced tree like an AVL tree or Red-Black tree, the height is \(O(\log n)\), which represents the worst-case depth traversed during the removal process.

Given that we are considering a "full" binary search tree, which implies it's typically balanced:

The worst-case performance for the remove method in a well-balanced BST should be:

a. \(O(\log n)\)

27. What is the worst-case performance of the getEntry method in a full binary search tree with linked nodes?

a. O(log n)

b. O(n)

c. O(1)

d. O(n²)

a. O(log n)

\(O(\log n)\): This would be the case if the tree is balanced, such as in an AVL tree or a Red-Black tree, where the height of the tree is \(O(\log n)\). Because searching in a BST involves traversing from the root to a leaf, the time complexity would be proportional to the tree's height.

Given that we are dealing with a "full" binary search tree, which implies it's typically balanced:

The worst-case performance for the `getEntry` method in a balanced BST is:

a. \(O(\log n)\)