MATH 227: 10.4 (Calculus in Polar Coordinates)

Find the area of the region that is bounded by the given curve, r = e^(-θ/10), π/2 ≤ θ ≤ π

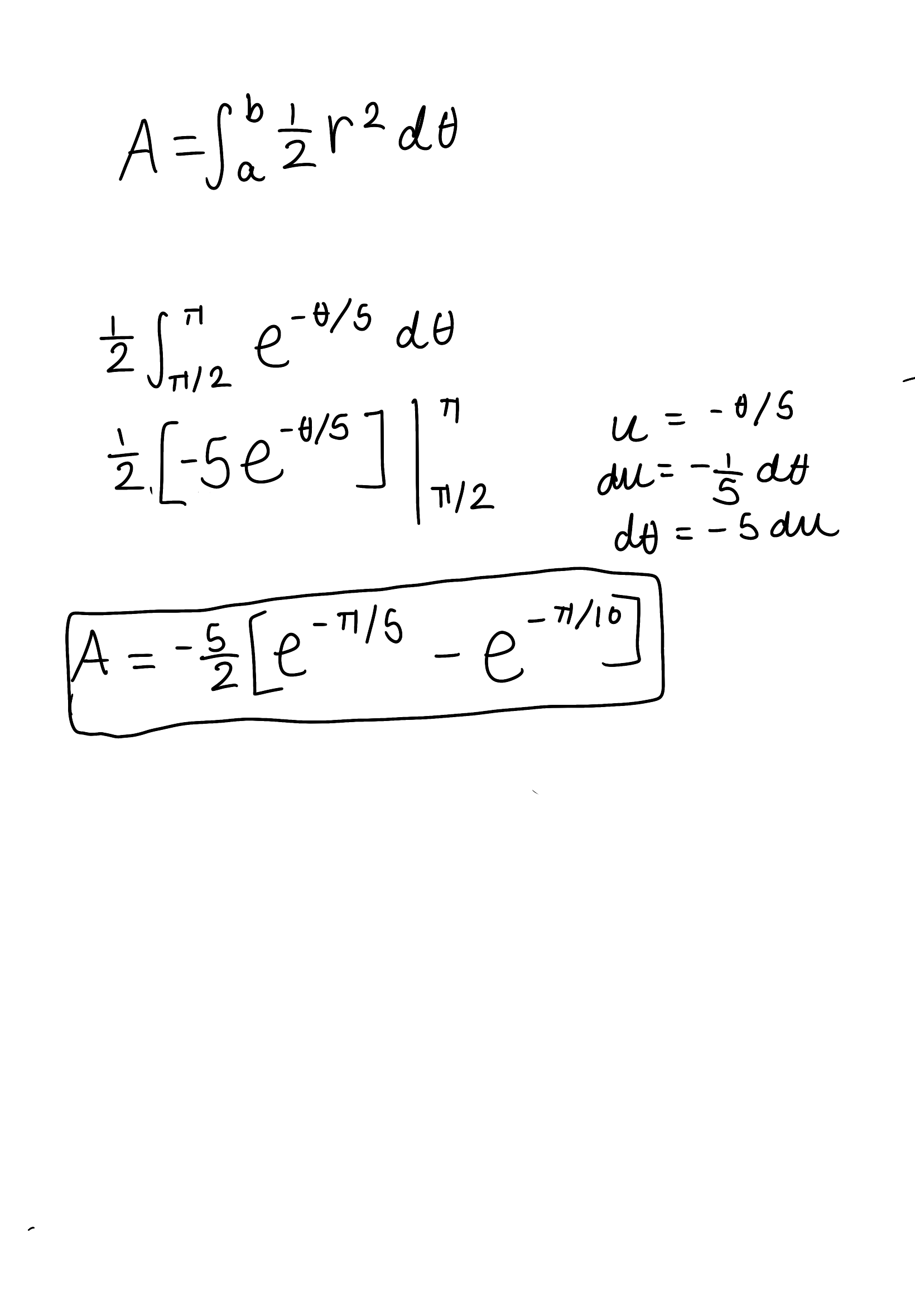
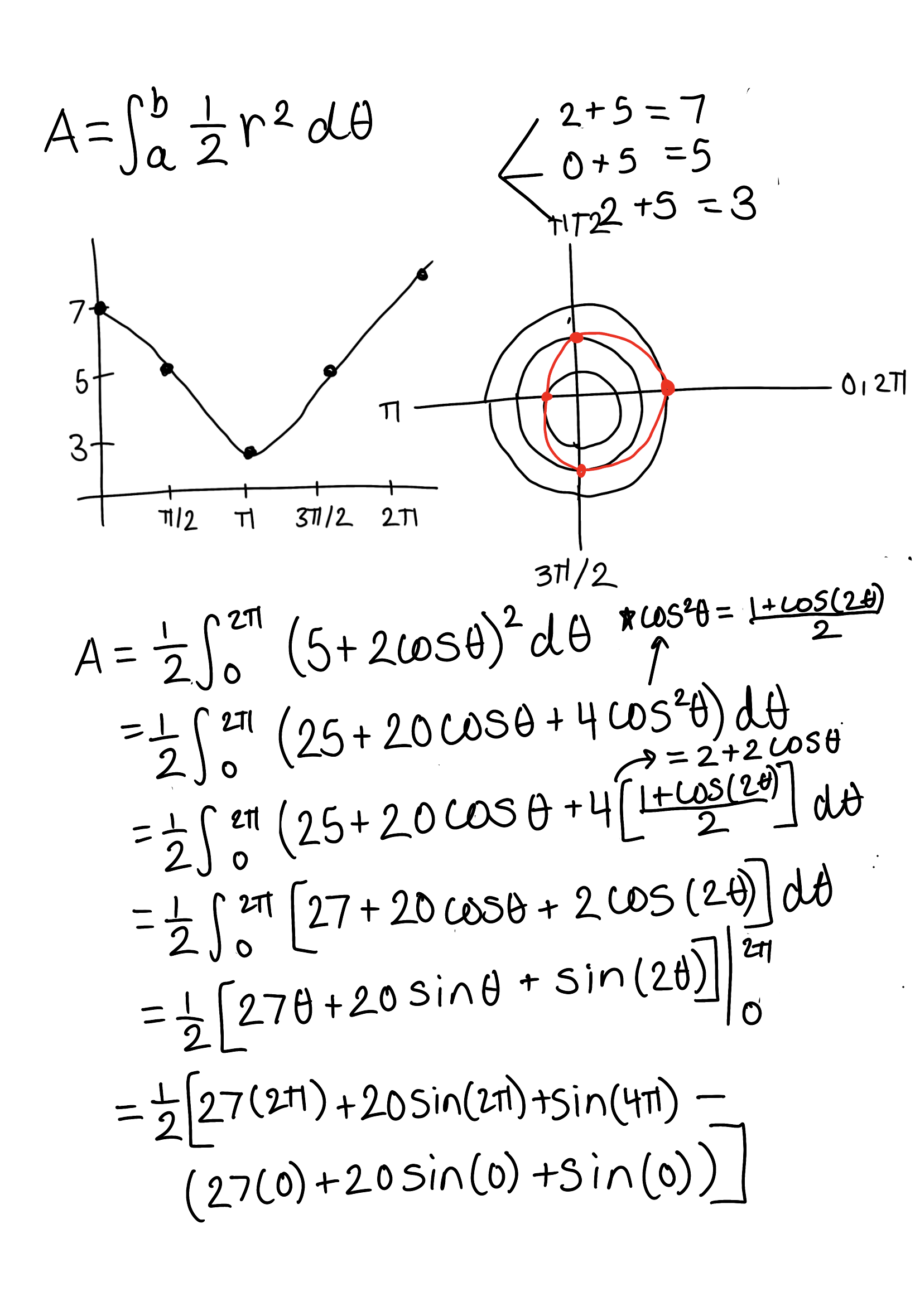
Find the area that encloses r = 5 + 2 cos(𝜃)

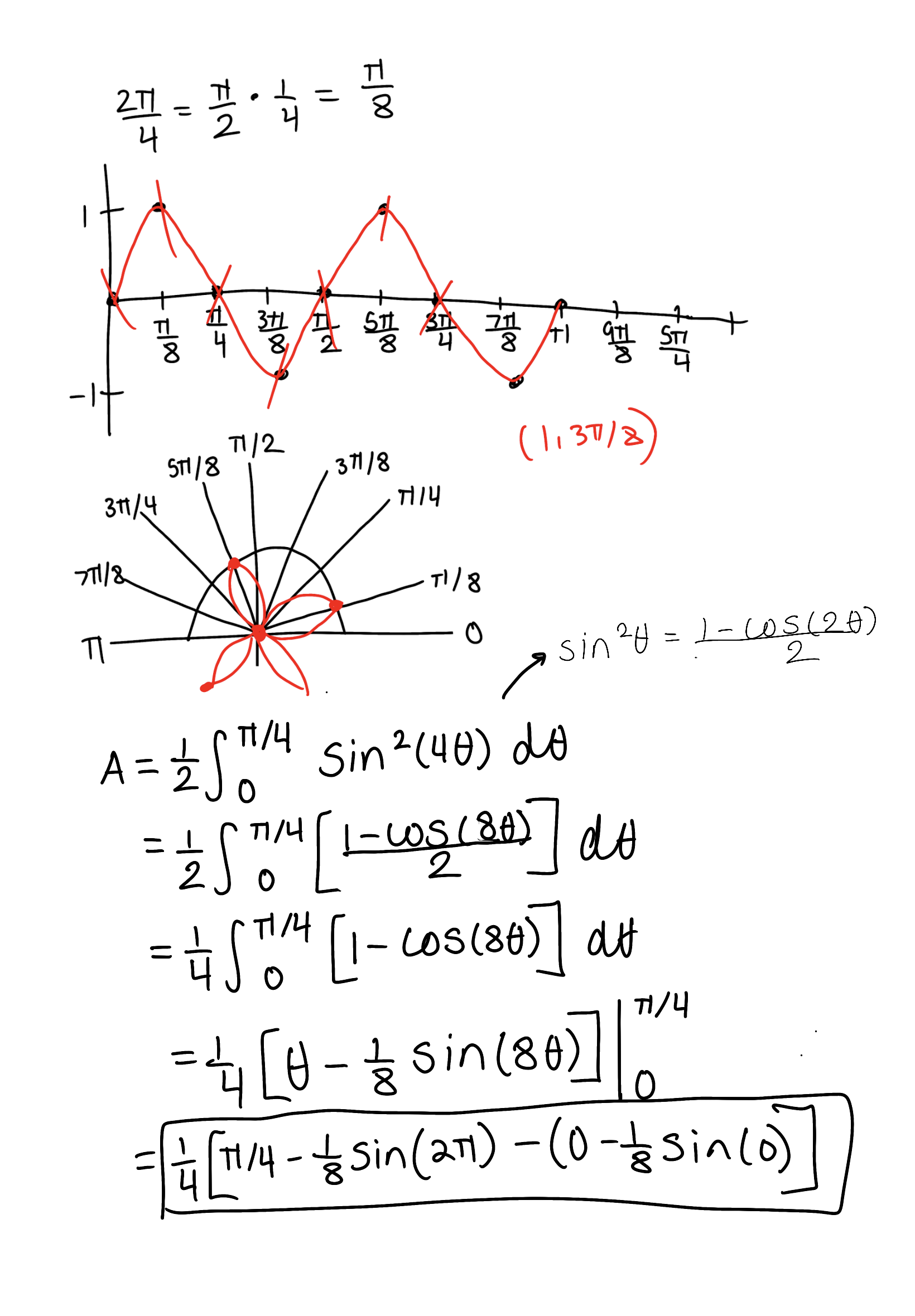
Find the area of the region enclosed by one loop of the curve r = sin(4𝜃)

Find the area of the region that lies inside the first curve and outside the second curve. r = 14 cos(𝜃), r = 7

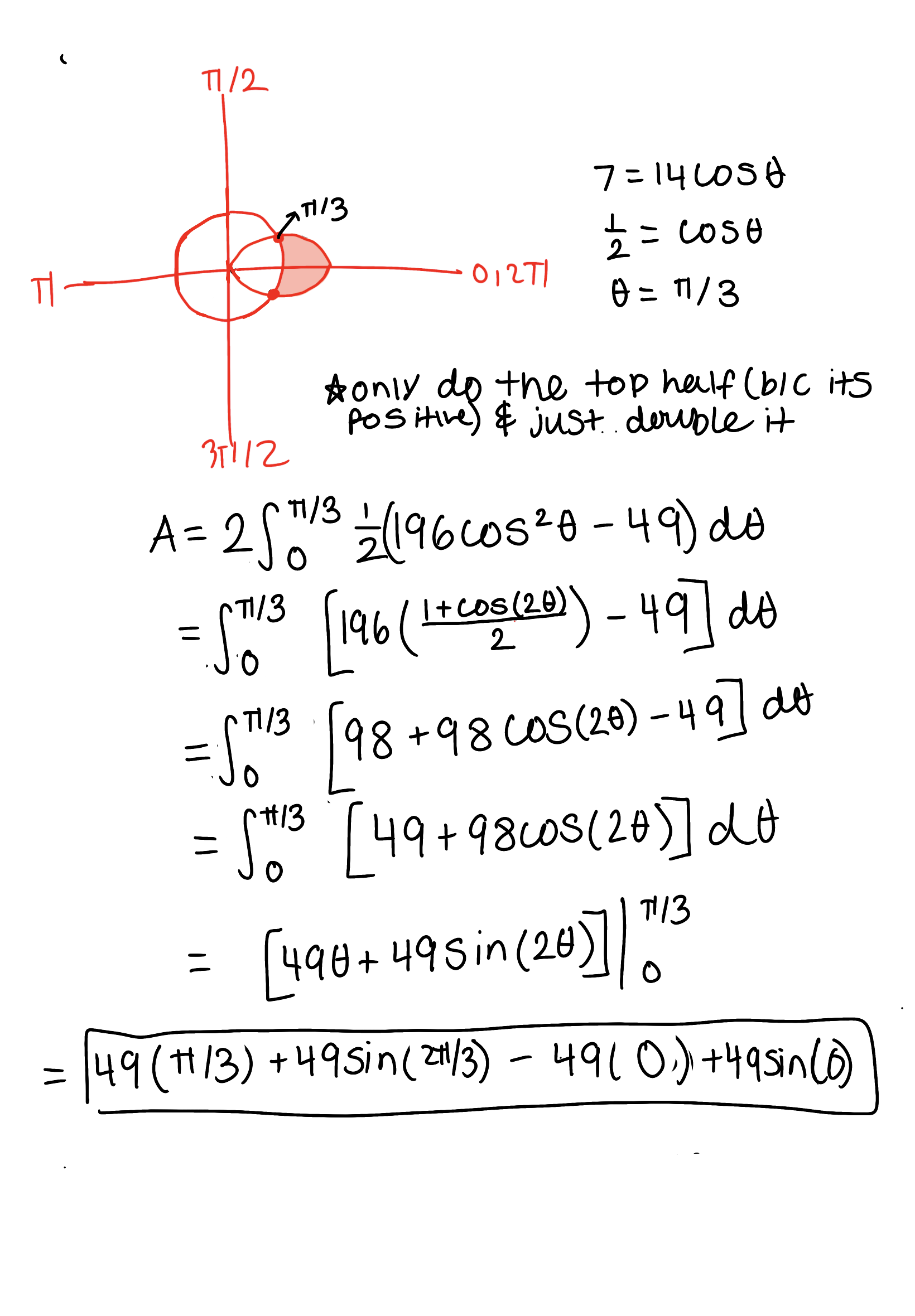
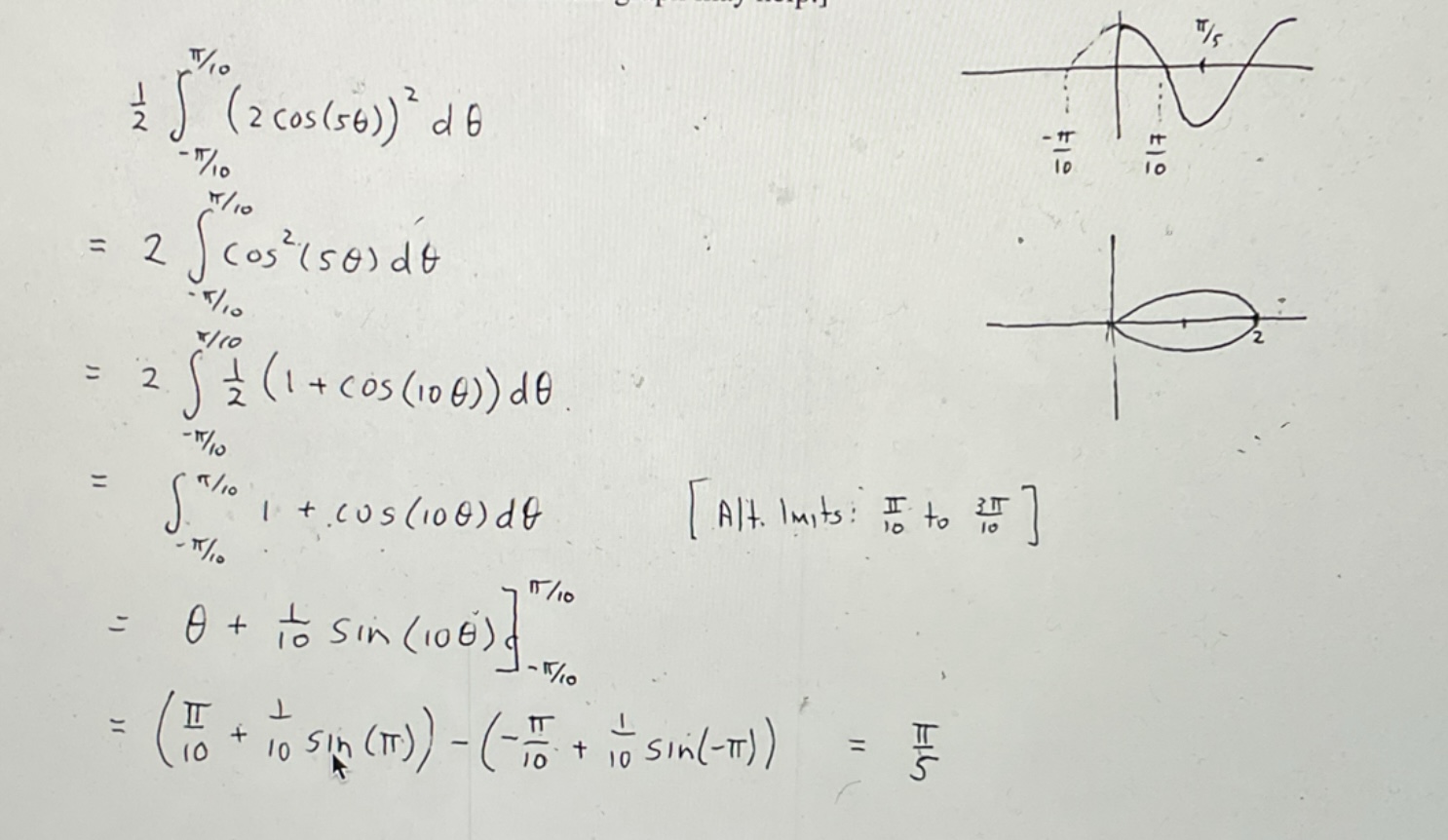
A. Find the area enclosed by one of the petals of the curve r = cos(2θ)

B. Set up the integral to find the area of the entire curve

B. You would right the same thing for part A where you only use one half of the petal, but instead of multiplying the integral by 2, you would multiply it by 8. If you wrote the integral in part A by doing the positive and negative bounds as opposed to just doing the positive bound and the other bound be 0, you would multiple the integral by 4

Find the area enclosed by one loop of the circle r = 2cosθ

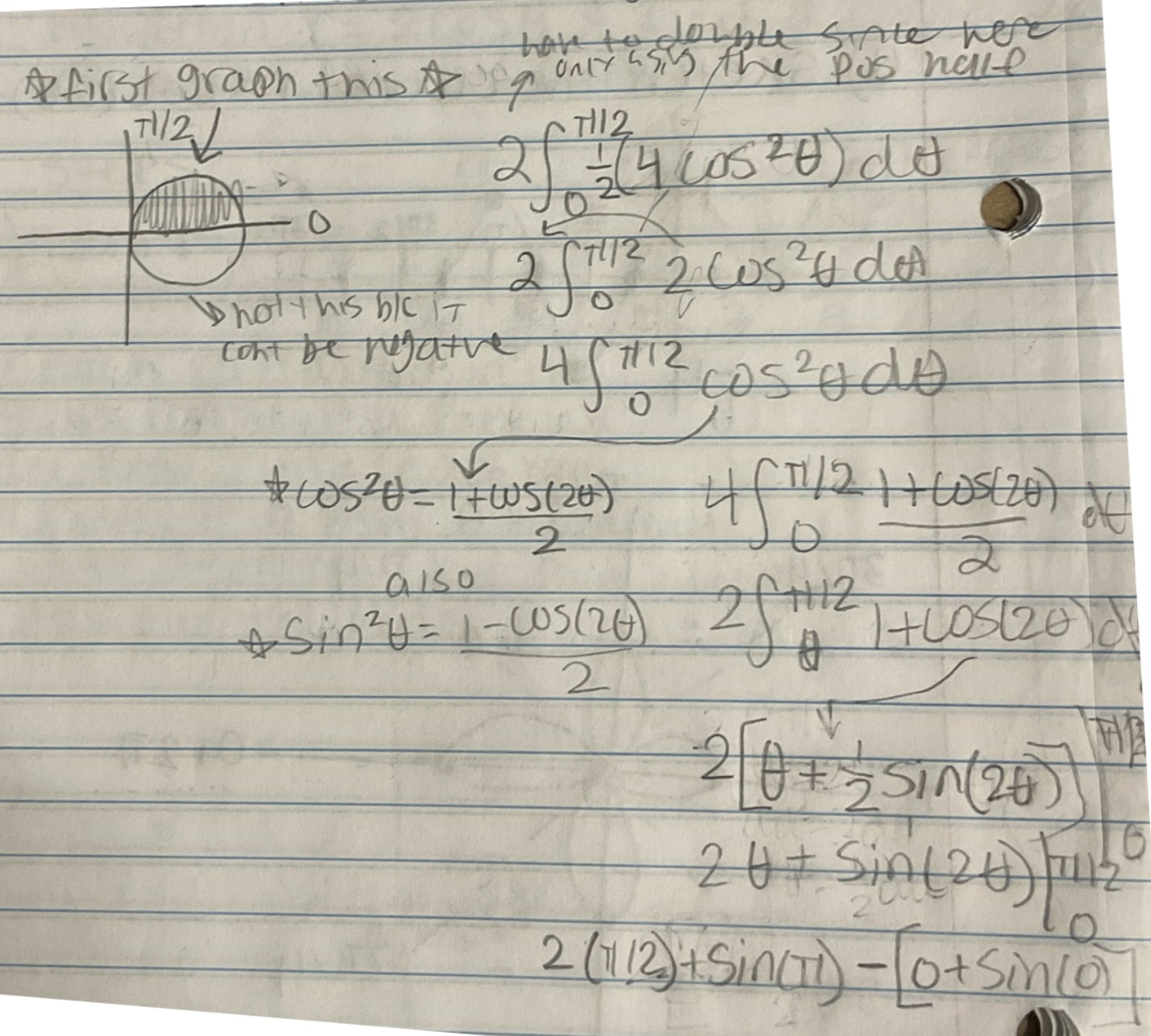
Find the area of the region that lies inside the first curve r = 3sin𝜃 and outside the second curve r = 1 + sin𝜃

Find the arc length of the curve r = 2cosθ, 0 ≤ 𝜃 ≤ 𝜋

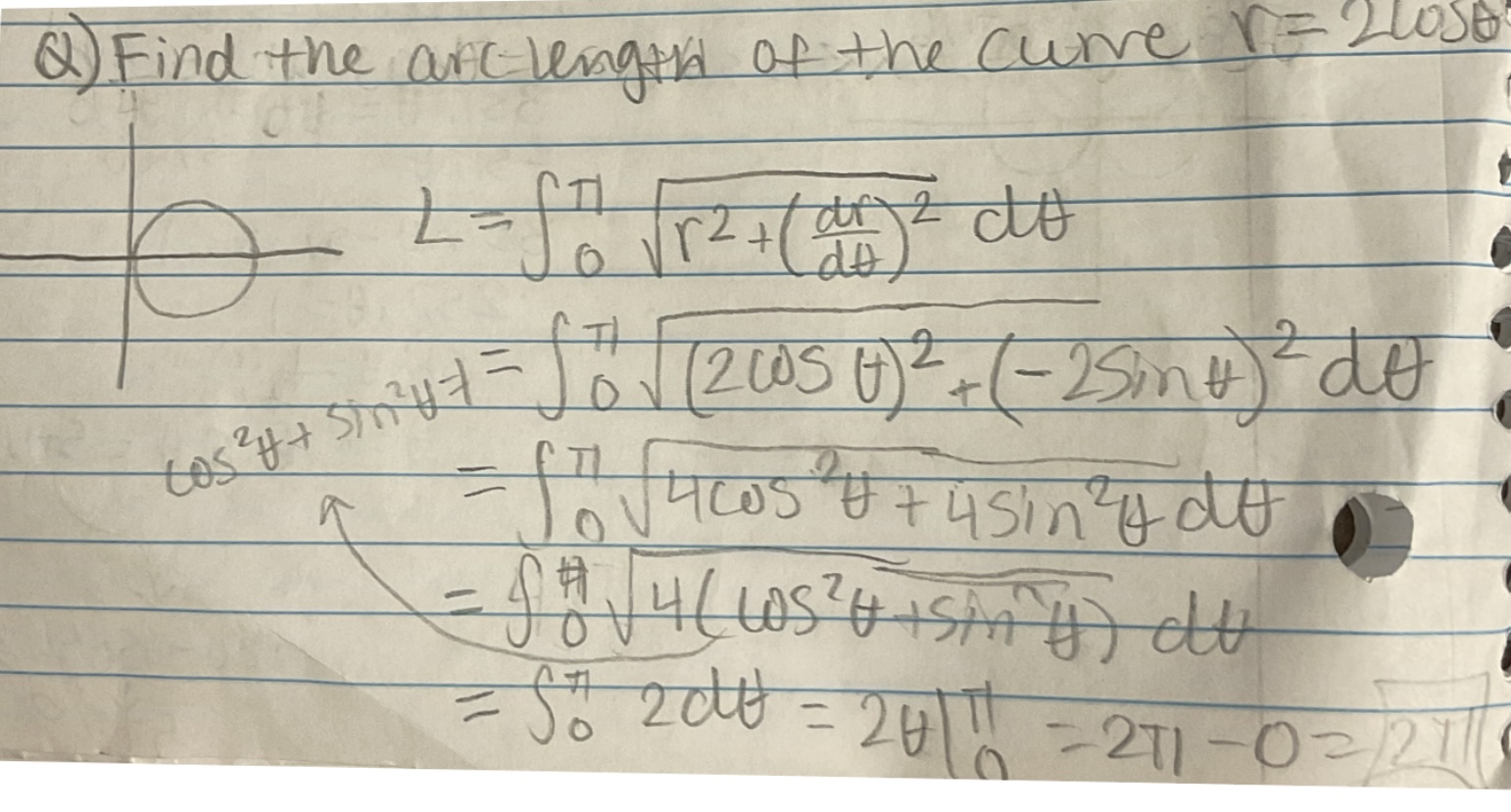
Find the slope of the tangent line to the polar curve r = 2cosθ, when θ =π/3

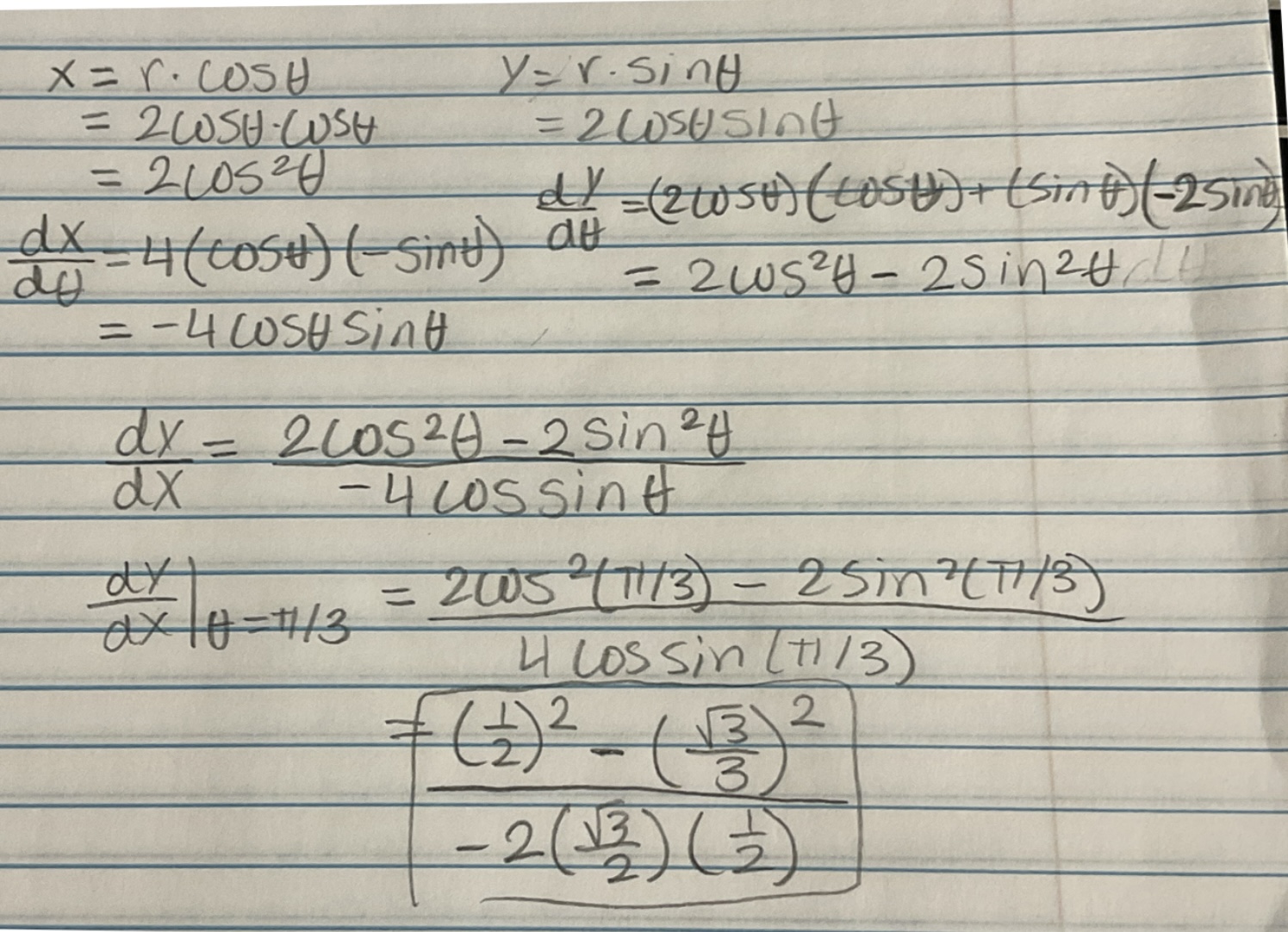
Find the slope of the tangent line to the polar curve r = 9/θ, when θ = π

Find the slope of the tangent line to the polar curve r = cos(θ/3), when θ = π

Find the exact length of the polar curve r = θ², 0 ≤ 𝜃 ≤ 3𝜋/2