ap precalc is my 13th reason

you got this bestie!!

RECOGNIZING CHANGE PATTERNS IN FUNCTIONS (starts on next card)

linear

rate of change is constant on any interval

quadratic

2nd differences of output values are constant over consecutive equal-length input value intervals

polynomial (degree n)

nth differences of output values are constant over consecutive equal-length input value intervals

exponential

output values are proportional over equal-length input value intervals

logarithmic

proportional input values result in constant change in output values

RATES OF CHANGE (starts on next card)

average rate of change (AROC)

the aroc of f(x) over the interval [a, b] is the slope of the line between the points

rate of change (ROC)

roc of f at a point refers to the slope of the graph at that point

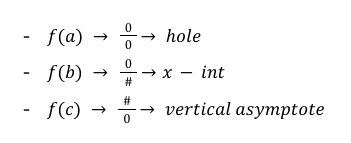
BEHAVIOR OF RATIONAL FUNCTIONS (starts on next card)

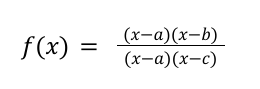
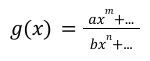
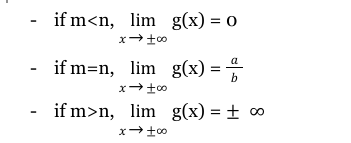
SEQUENCE FORMULAS (starts on next card)

arithmetic

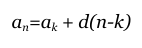
geometric

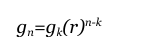
PROPERTIES OF EXPONENTS (flip this card)

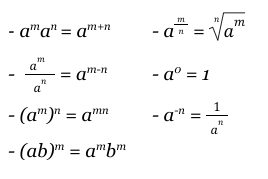
PROPERTIES OF LOGARITHMS (flip this card)

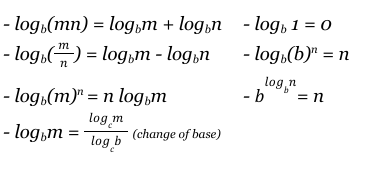
TRANSFORMATIONS (starts on next card)

g(x) = a f(b(x+h))+k

(vertical changes)

stretch if |a|>1

compression if |a|<1

reflection if a is negative

g(x) = a f(b(x+h))+k

(horizontal changes)

stretch if |b|>1

compression if |b|<1

reflection if b is negative

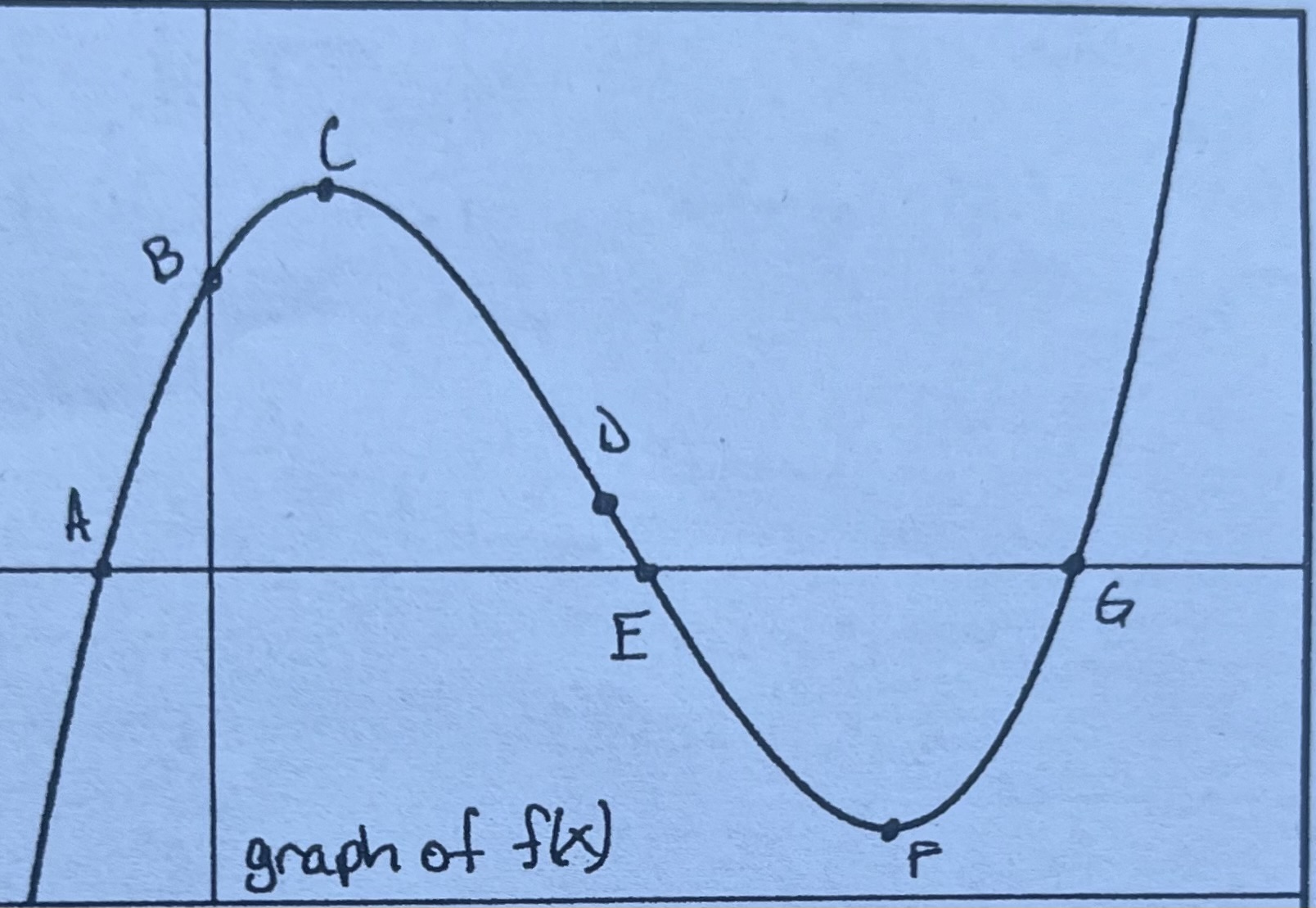
FUNCTION BEHAVIORS (flip this card)

-∞ to D: f(x) is concave down. roc is decreasing.

D to ∞: f(x) is concave up. roc is increasing.

C to F: f(x) is decreasing. roc is negative.

F to ∞: f(x) is increasing. roc is positive.

A to E: f(x) is positive

E to G: f(x) is negative

C and F: extrema (C - relative max; F - relative min)

D: point of inflection (change in concavity)

INVERSE FUNCTIONS (starts on next card)

numerically

if f(a) = b then f^-1(b)=a

graphically

f^-1(x) is the reflection of f(x) over the y=x

algebraically

to find f^-1(x), switch x and y on f(x) and solve for x

verbally

f^-1(x) uses the opposite operations of f(x) in the reverse order

• f^-1(x) is a function if every output value of f(x) comes from a unique input value

• a function that is either strictly increasing or strictly decreasing is invertible

• the domain of f^-1(x) is the range of f(x) and vice versa

extra note?? or smth ig??? idk atp

f^-1(f(x)) = f(f^-1(x)) = x

for all x in the domain of either function

IDENTITIES (starts on next card)

pythagorean

• sin²θ + cos²θ = 1

• tan²θ + 1 = sec²θ

• cot²θ + 1 = csc²θ

reciprocals (pythagorean)

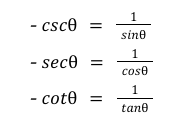
quotients (pythagorean)

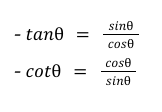
angle sum/difference

• sin (a+b) = (sin a)(cos b) + (cos a)(sin b)

• sin (a-b) = (sin a)(cos b) - (cos a)(sin b)

• cos (a+b) = (cos a)(cos b) - (sin a)(sin b)

• cos (a-b) = (cos a)(cos b) + (sin a)(sin b)

SINE COSINE COSINE SINE COSINE COSINE SINE SINE AHHAHAHHHHHHHHH ok sorry

double angle

• sin 2θ = 2 sinθ cosθ

• cos 2θ = cos²θ - sin²θ

  • = 2 cos²θ - 1

  • = 1 - 2 sin²θ

SINE/COSINE GRAPH PROPERTIES (starts on next card)

f(x) = a sin (b(x+c)) + d

• y = sinx: starts at midline and does upward

• y = cosx: starts at maximum and goes downward

|a| = amplitude d = midline

|a| + d = maximum -e = phase shift

|a| - d = minimum (2π)/b = period

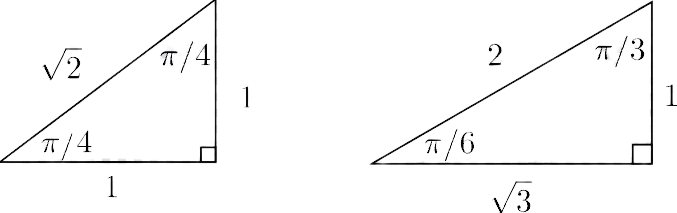
SPECIAL RIGHT TRIANGLES (flip this card)

INVERSE TRIG FUNCTIONS (can be written as sin^-1(x) or arcsin(x) (flip this card)

	f(x) = sin-1x	g(x) = cos-1x	h(x) = tan-1x
input	ratio of sides or y-coordinate on unit circle	ratio of sides or x-coordinate on unit circle	ratio of sides or slope of terminal side of θ
output	standard position angle	standard position angle	standard position angle
domain	x→[-1,1]	x→[-1,1]	x→[-∞,∞]
range	y→[(-π/2), (π/2)] (quad 1 and 4)	y→[0, π] (quad 2 and 3)	y→[(-π/2), (π/2)] (quad 1 and 4)

POLAR COORDINATES (starts on next card)

rectangular (x,y) → polar (r,θ)

• r = √x² + y²

• tan^-1(|y/x|) = reference angle (use quadrant and reference angle to find θ)

polar (r,θ) → rectangular (x,y)

• x = r cosθ

• y = r sinθ

polar form of a complex number

a + bi = r(cosθ + isinθ)

PASCAL’S TRIANGLE (flip this card)

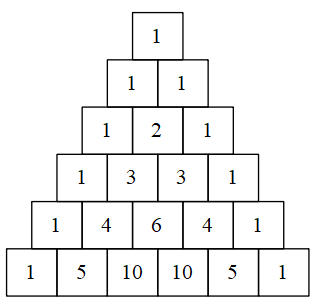
JUSTIFICATIONS/FRQ TERMINOLOGY (starts on next card)

a function is increasing over an interval of its domain if:

for all a and b in the interval, if a < b, then f(a) < f(b)

a function is decreasing over an interval of its domain if:

for all a and b in the interval, if a < b, then f(a) > f(b)

YOU GOT THIS WOOOOOO!!!!!!