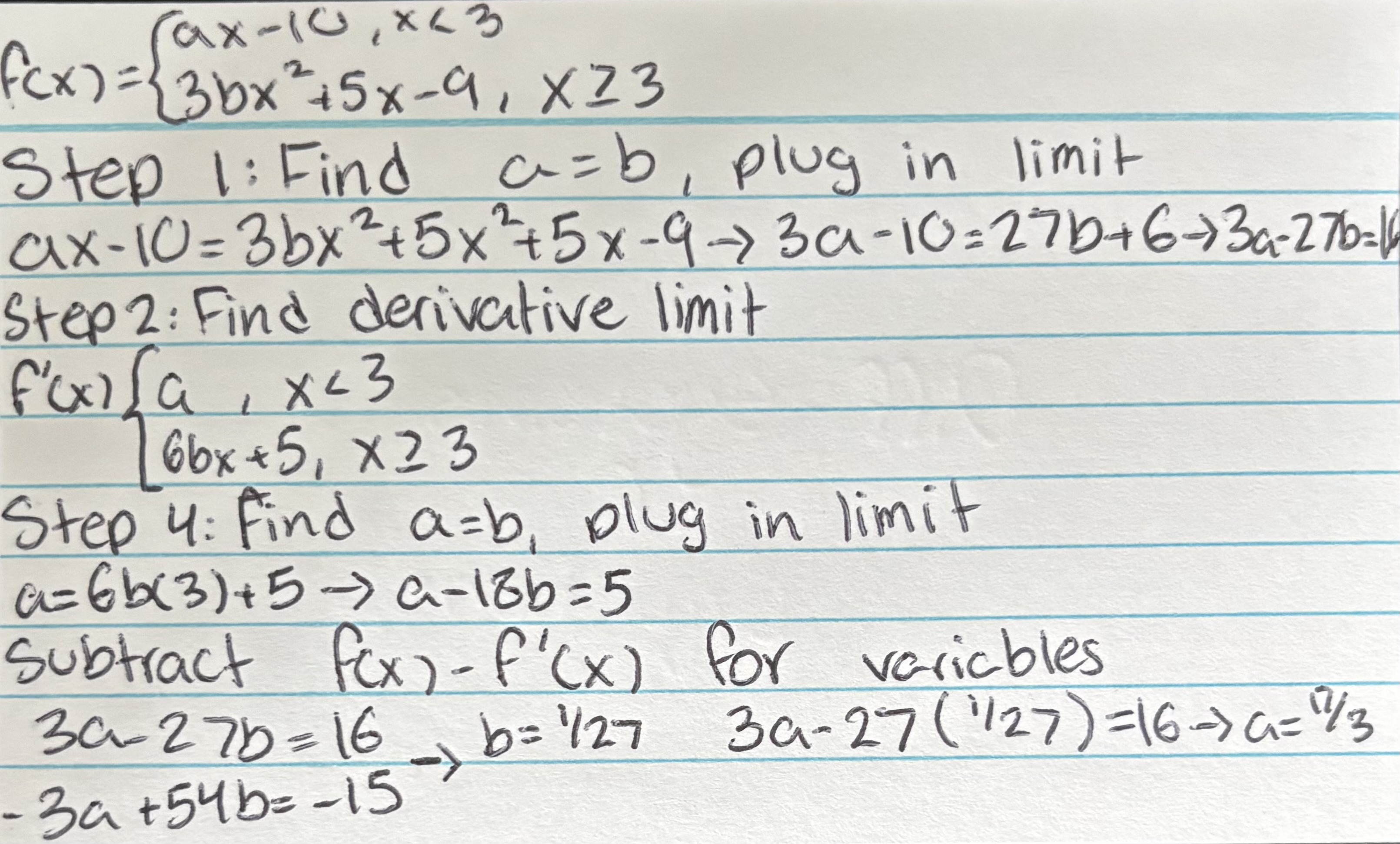PRECALC UNIT 11

Derivative with add/minus

f′(x)

Derivative with multiply

f′(x)=f'g+fg'

Derivative with division

f′(x)=(f'g-fg')/g²

Derivative with e

f′(x)=e^x

Derivative with ln

f′(x)=#/x

Ex:(3/x)

Derivative with logs

f′(x)=1/(x ln (log number))

Ex:(log₂ x -> 1/x ln 2)

sinx

cosx

cosx

-sinx

tanx

-sec²x

cscx

(-cscx)(cotx)

secx

(secx)(tanx)

cotx

-csc²x

Slope of secant line

(f(x₂)-f(x₁))/x₂-x₁

Slope of tangent line

lim(h->0)=(f(x+h)+f(x)/h)

Radical derivative

normal, except IF NEGATIVE CHANGE LEVEL

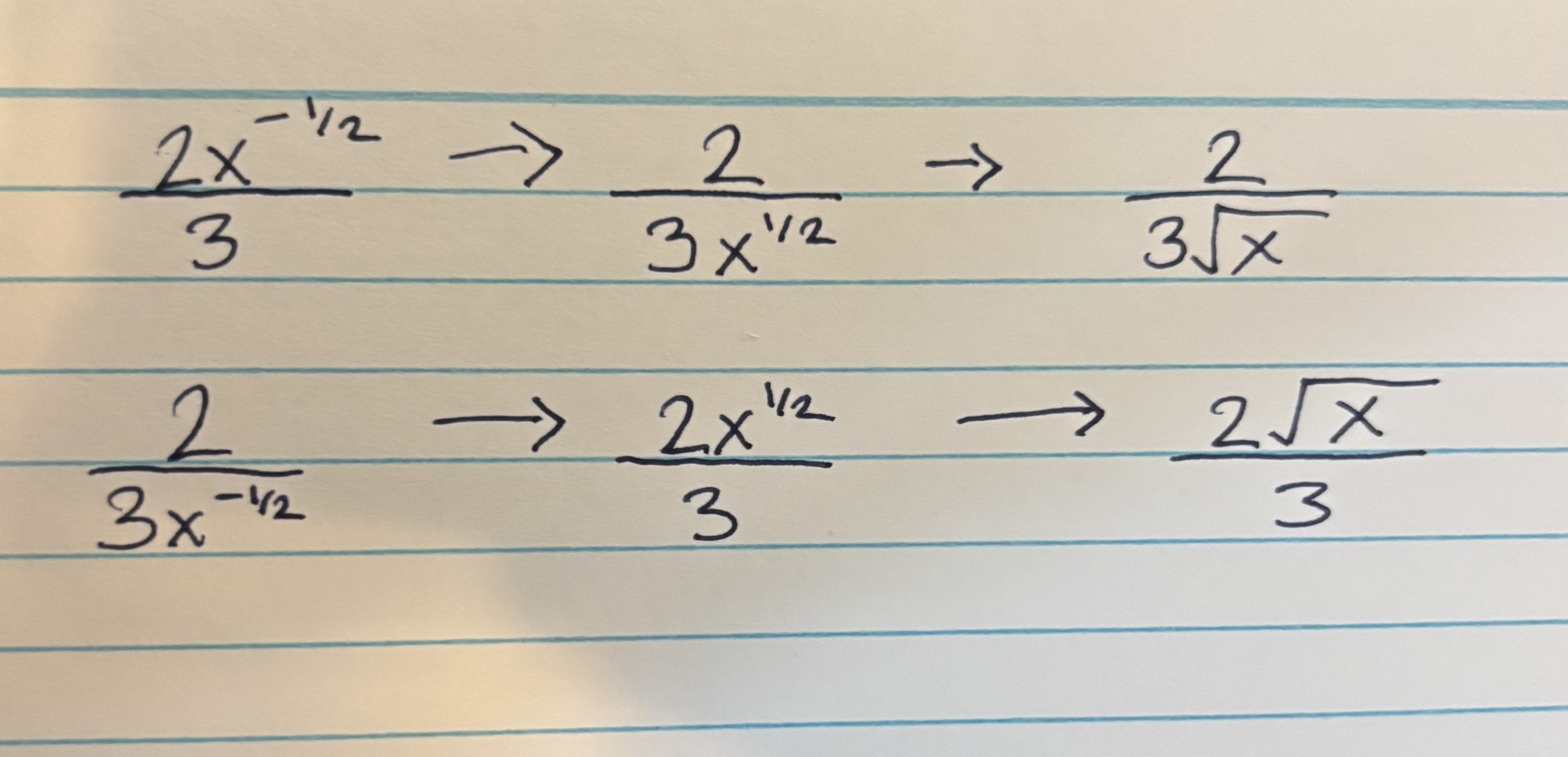
Derivative with exponentials

f′(x)=#^x ln #
Ex:(3^x ln 3)

Equation of a tangent line (given x=#)

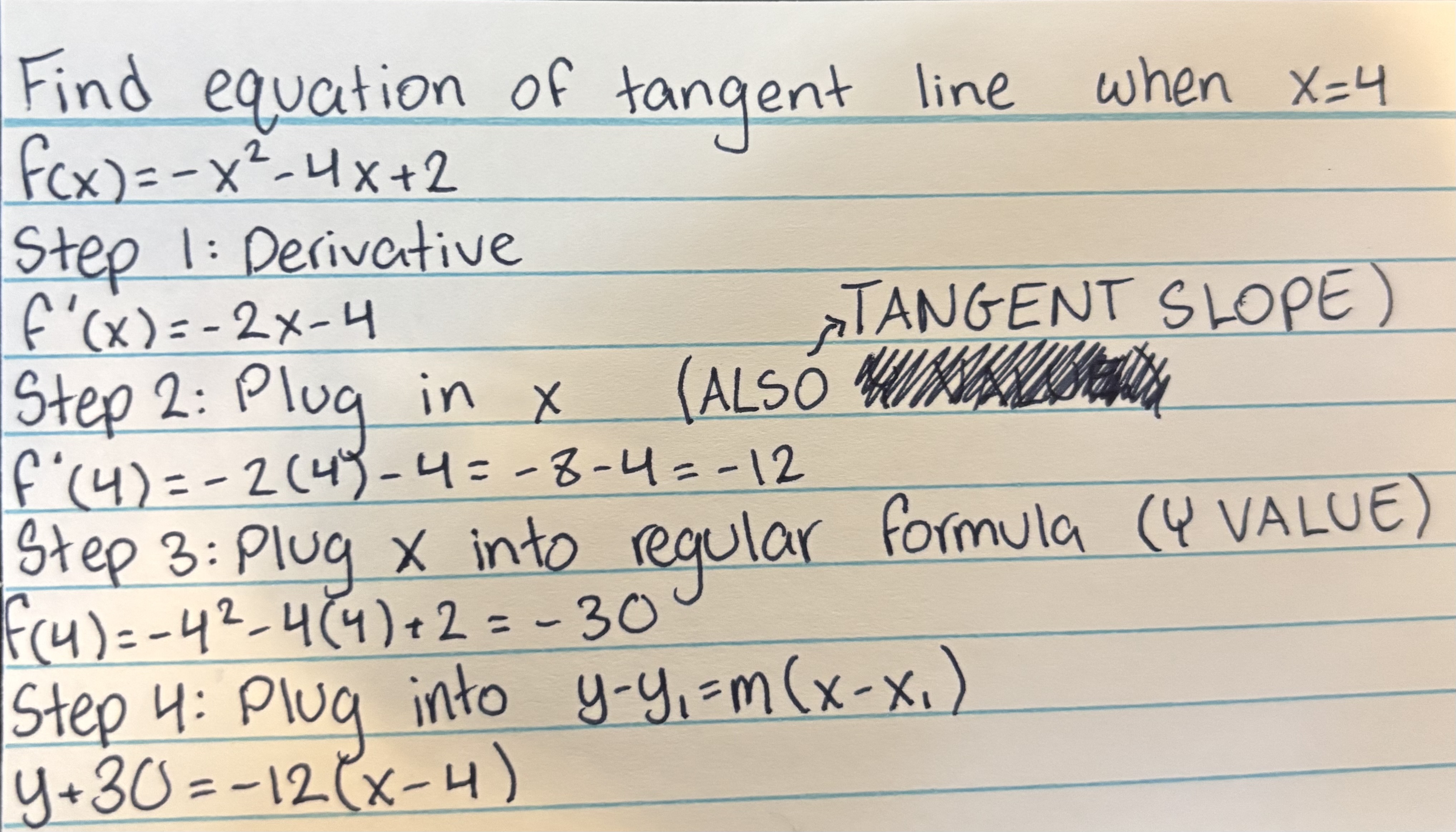
Points of a tangent line given slope

Chain Rule

f′(x)=(g(x)) · g′(x)

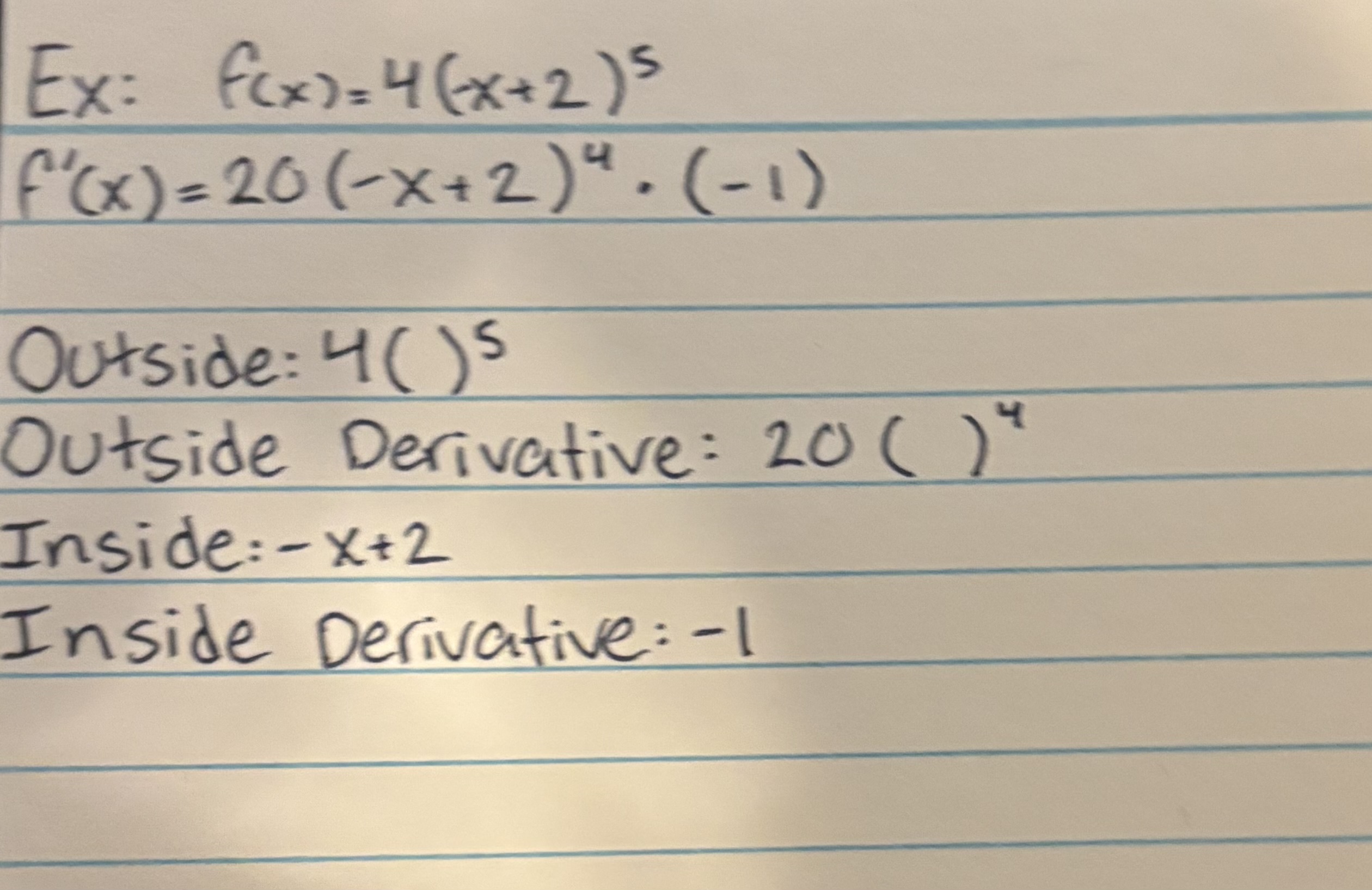
When the Trig Derivative has exponential

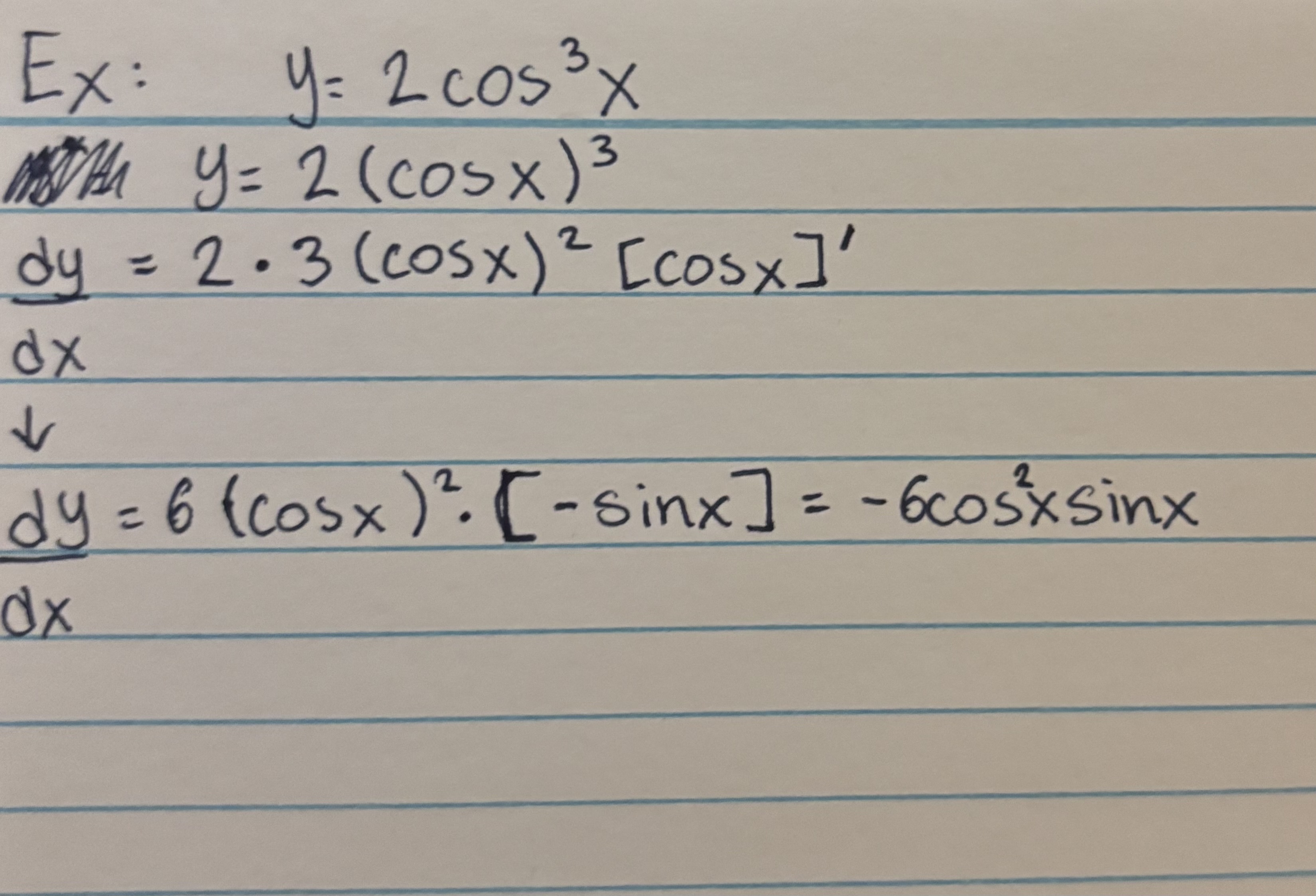
When the Trig Derivative does NOT equal just x

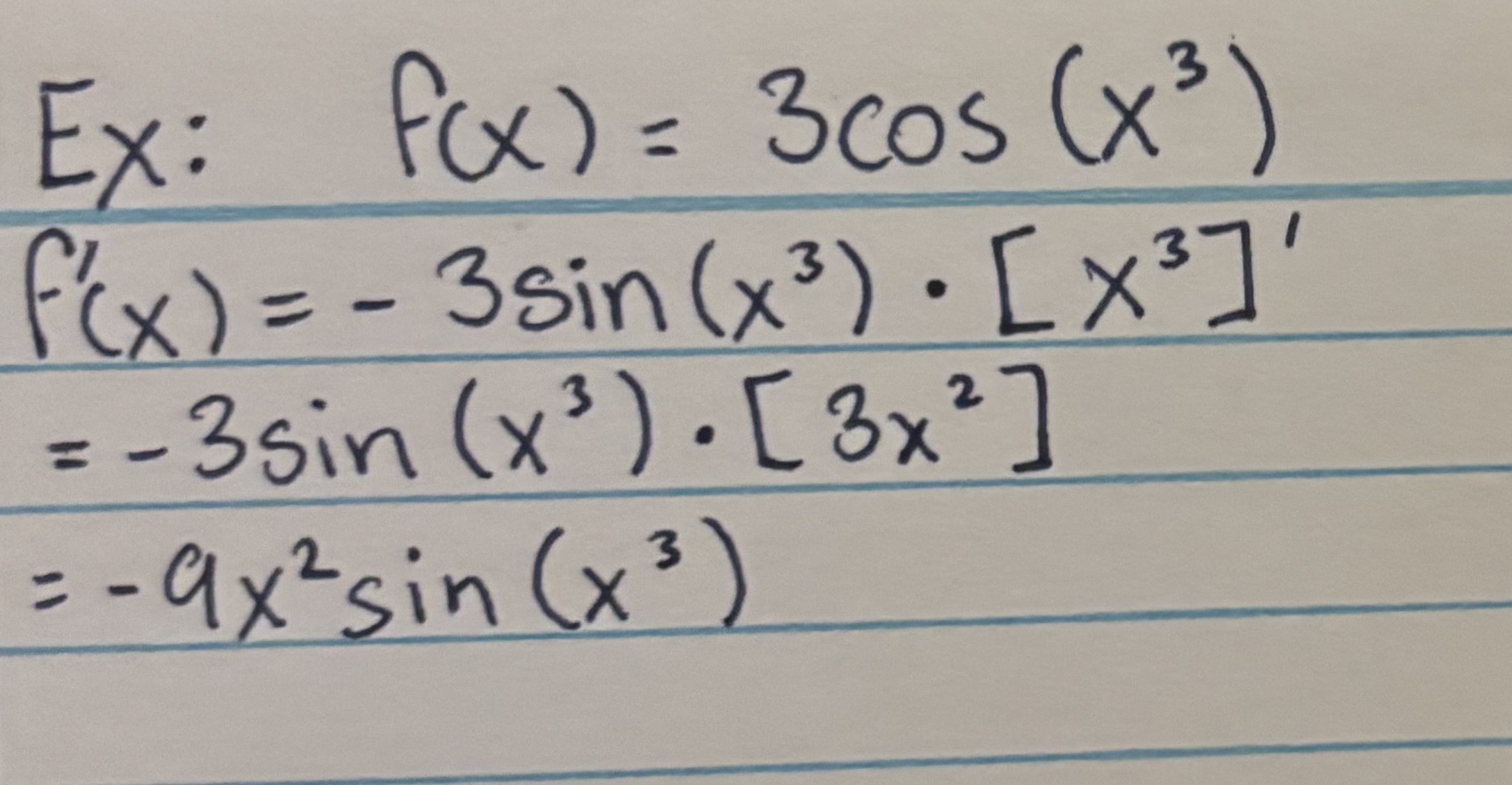
Derivative of e (Chain Rule)

f′(x)=e^xxx· (Derivative of xxx)

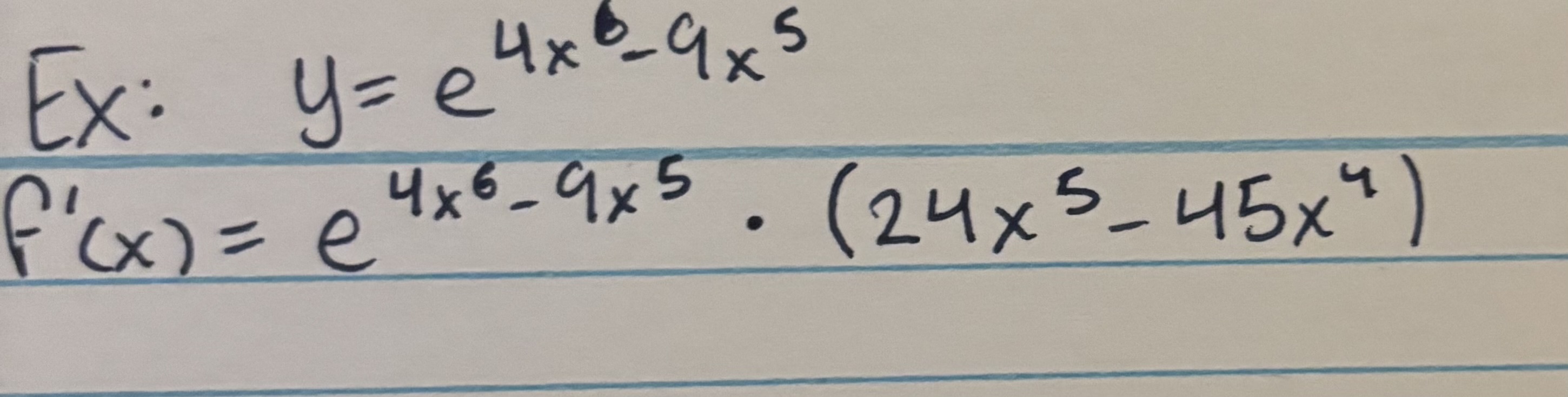
Derivative of exponential with base NOT e (Chain Rule)

f′(x)=#^xxx·ln#·(Derivative of xxx)

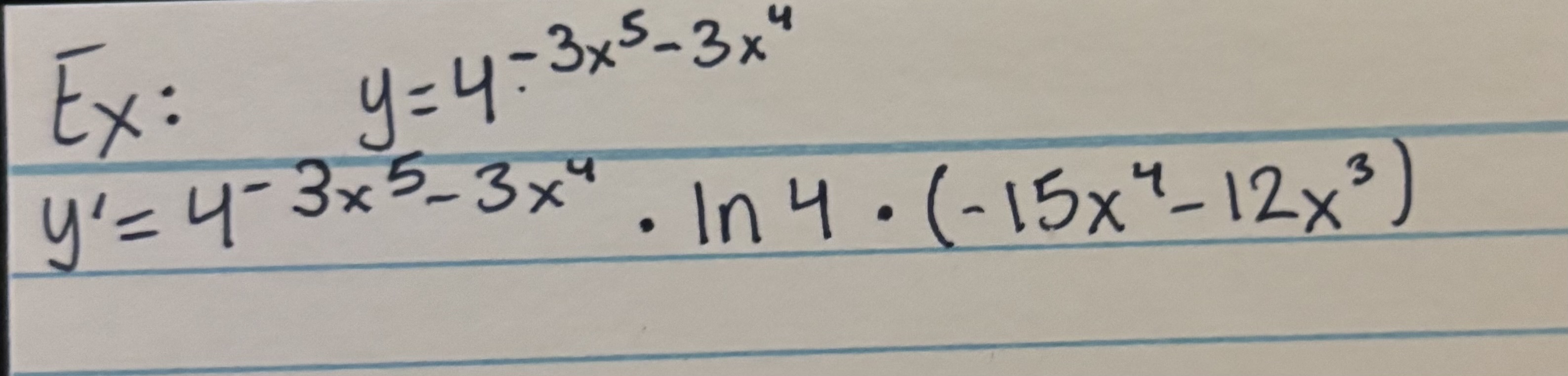
Derivative of ln (Chain Rule)

f′(x)=(1/x)·(Derivative of #)

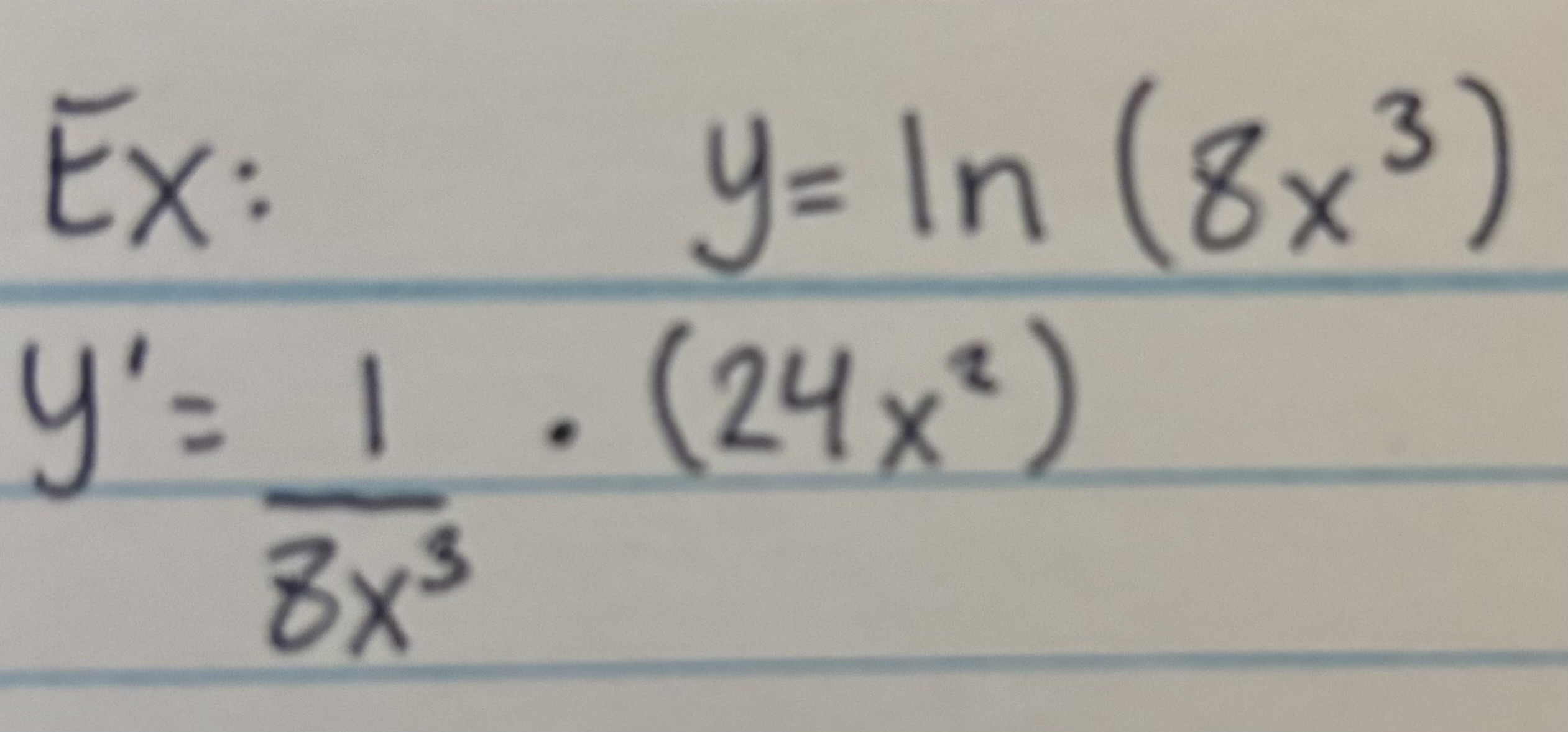
Derivative of log (Chain Rule)

f′(x)=(1/x·ln(log#))·(Derivative of x)

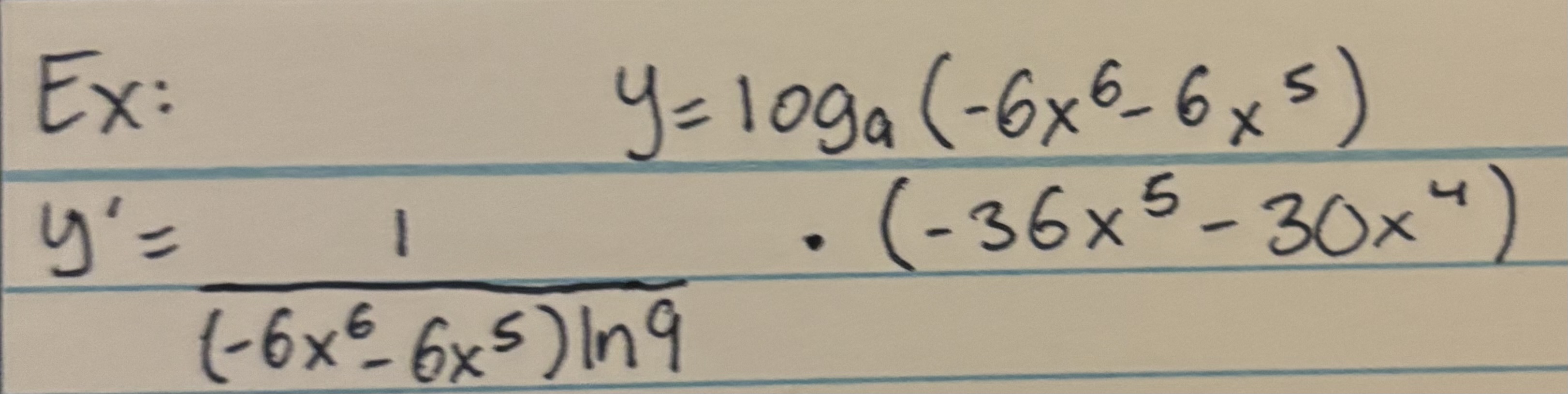
Implicit Differation: Solving for dy/dx

Differentiate like normal, but make all differentiated y values multiply by dy/dx

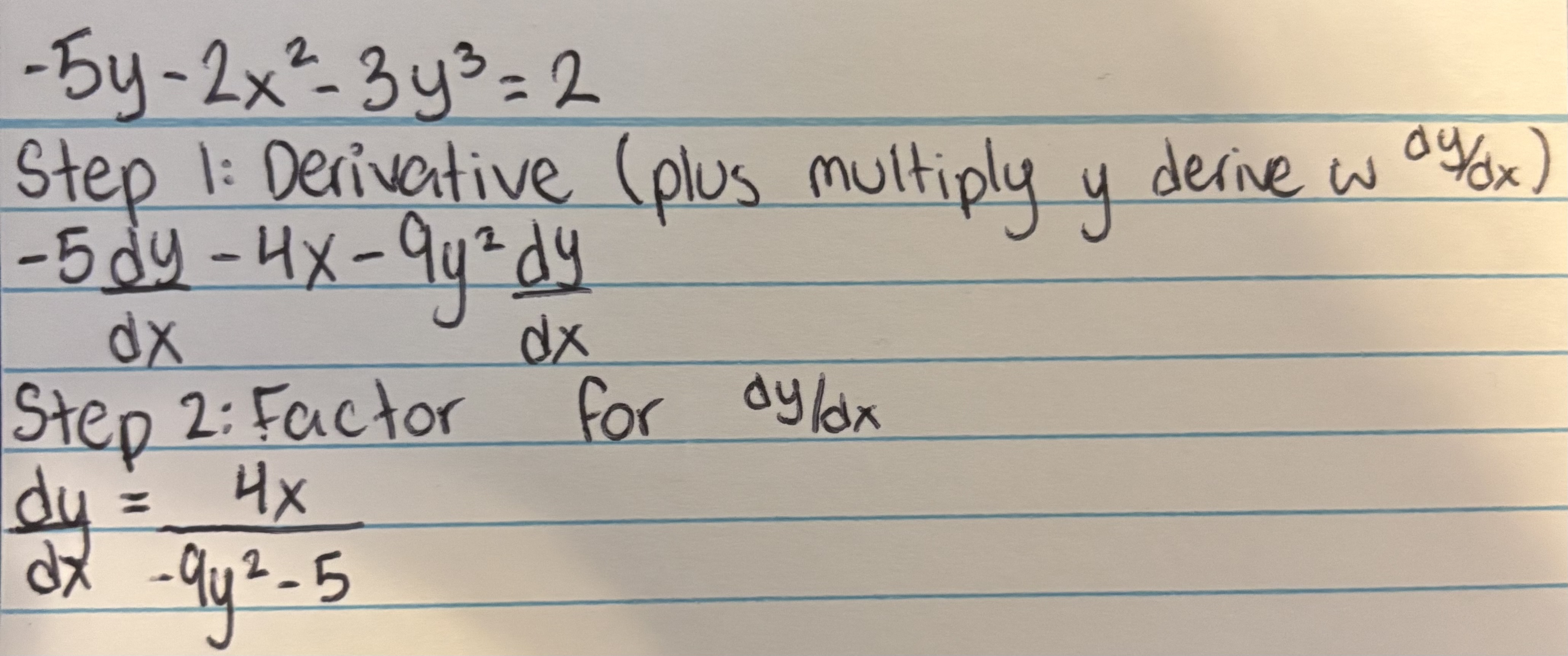
Implicit Derivative at a Point

Implicit differentiation the formula, plug in the point

Tangent lines with Implicit Derivative from a Point

Implicit differentiation the formula, plug in the point, plug coordinates and point(slope) into y-y₁=m(x-x₁)

Derivative Notation (Given external formula)

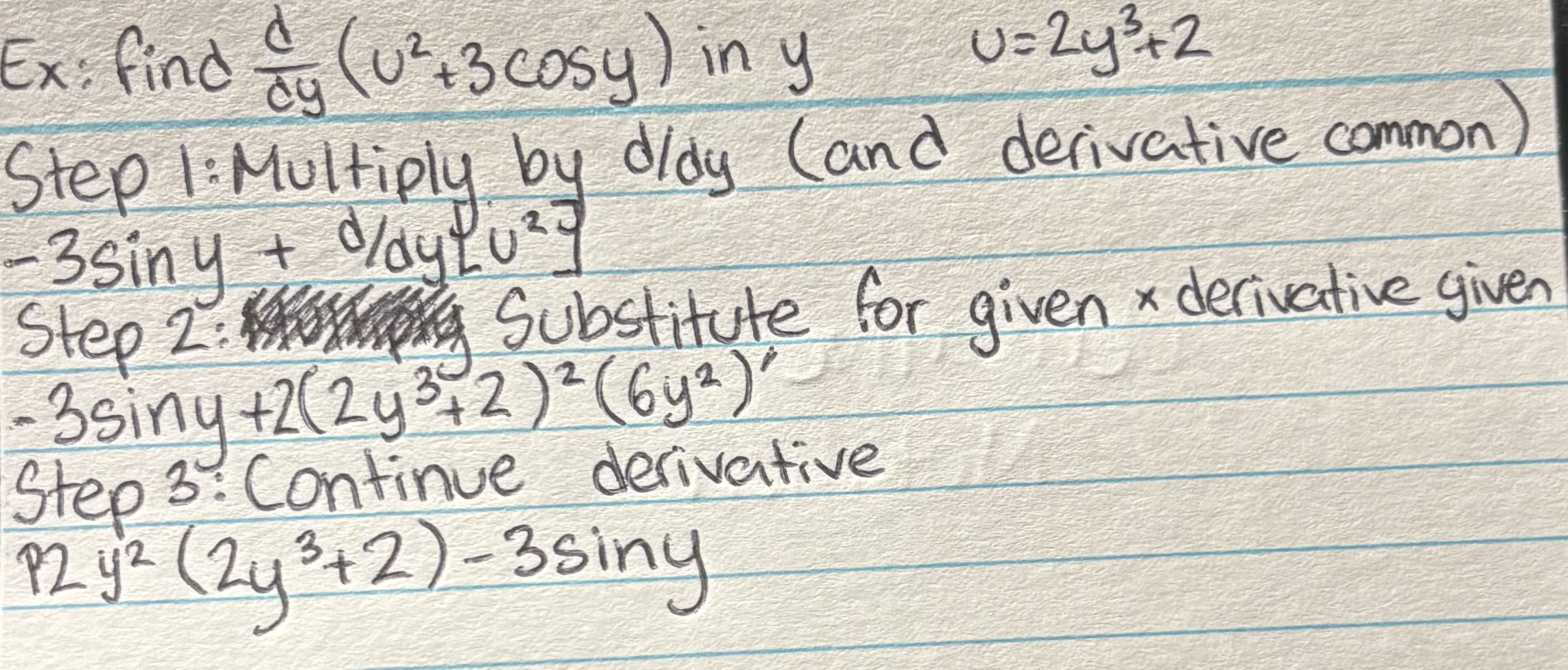
Implicit Differentiation with trig

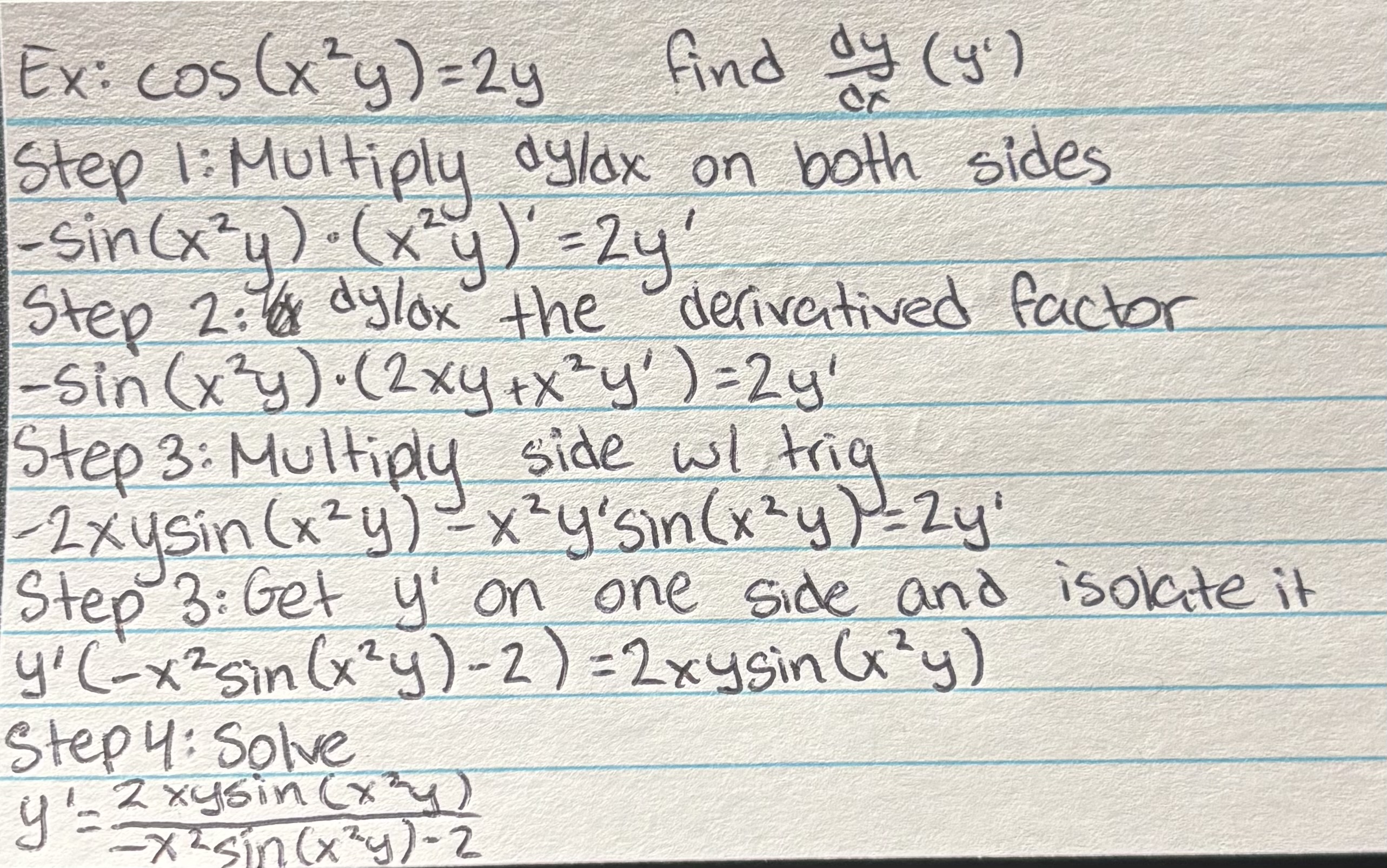
Implicit Derivative to find tangent line (when given x=#)

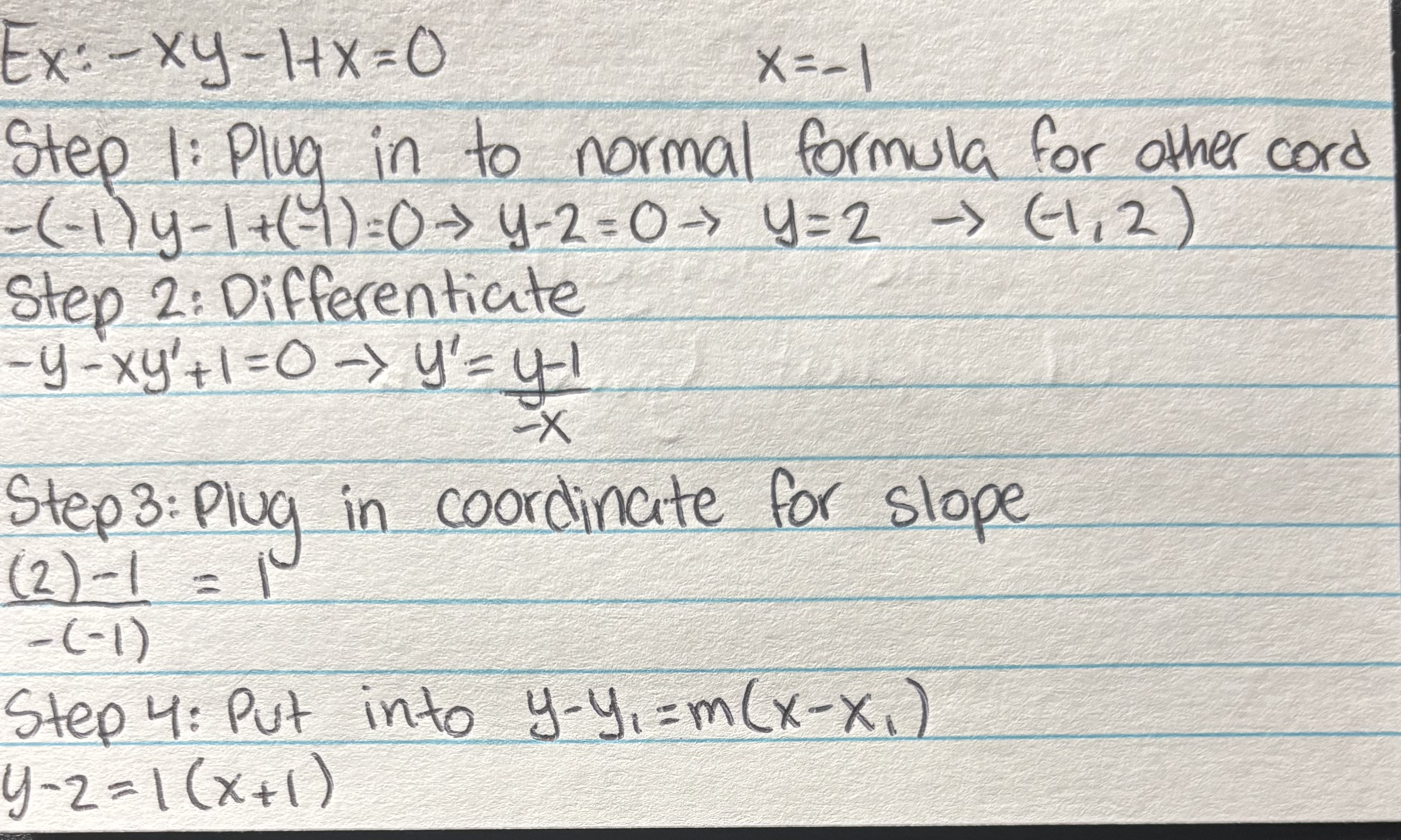
Second Derivative (with point)

L’Hopital’s Rule

1. Find the Limit of the top and bottom separately

2. Put it together, IF it equals an actual number, apply rule

3. Find limit of derivative

4. Plug in the limit

Finding differentiability in a system of equations

1. Make all sections of the limit equal each other, putting all variables onto one side

2. Find derivative of each limit section, make equal to each other, and put all variables to one side

3. Put f(x)-f′(x), solving for one variable at a time