BIOSTATS- Exam 2

Density Curve

A smooth curve that represents the distribution of a continuous random variable. The area under the curve corresponds to probabilities, with the total area equal to one.

normal distribution

A symmetric, bell-shaped density curve that describes the probabilities of a continuous random variable. It is defined by its mean and standard deviation.

standard normal distribution

normal distribution but the μ = 0 and σ = 1

z-score

distance along horizontal scale (the # σ from the mean)

to get the area to the left of the graph

pnorm(x)

to get the area to the right of the graph

1 - pnorm(x)

to get the area between two values

pnorm(upper) - pnorm(lower)

critical value

a z score on the borderline separating those z scores that are significantly low or significantly high.

z_a

z score with an area of a to its right.

Central Limit Theorem

the distribution of sample means approaches a normal distribution as the sample size increases, regardless of the original population distribution.

how large must sample be for CLT

n ≥ 30

for a sample (n ≥ 30) OR the original population is normally distributed

the sampling distribution of the sample means will be approximately normally distributed.

μ_x̄ = μ

Mean of all values of x̄

σ_x̄ = σ/√n

Standard deviation of all values of x̄

Normal Quantile Plot

graph of points (x, y) where each x value is from the original set of sample data, and each y value is the corresponding z score that is expected from the standard normal distribution

normal distribution

the pattern of the points is reasonably close to a straight line and the points do not show some systematic pattern that is not a straight-line pattern

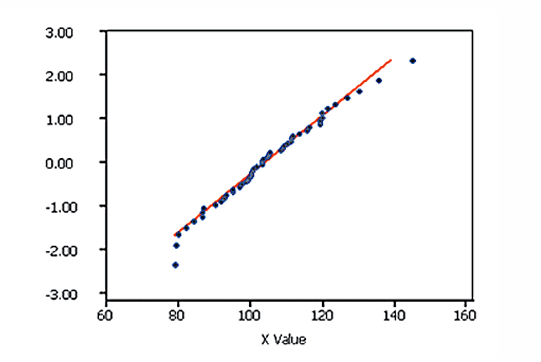
what distribution is this?

Normal

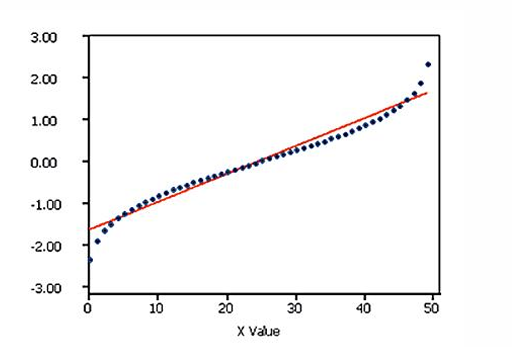
what distribution is this?

not normal; systematic patter

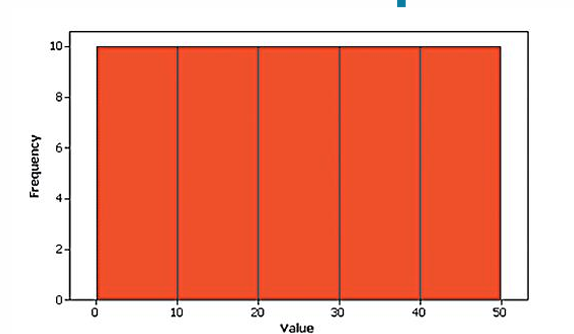
what distribution is this?

uniform

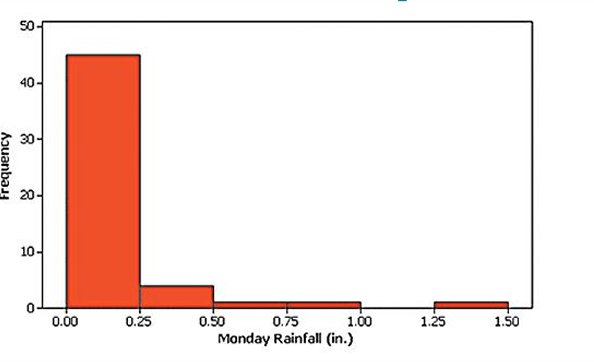
what distribution is this?

skewed

Data transformations

when you transform the data so that the modified values have a normal distribution.

hypothesis

a claim or statement about a property of a population.

hypothesis test (test of significance)

procedure for testing a claim about a property of a population

Null Hypothesis H₀

a statement that there is no effect, no difference, or no relationship in the population (any observed difference is due to random chance)

Alternative Hypothesis H₁

a statement that there is an effect, a difference, or a relationship in the population (suggests that the null hypothesis is not true)

significance level α

the probability of rejecting the null hypothesis when it is actually true, typically set at 0.05.

What is the sampling distribution for proportions?

Normal (z)

What are the requirements to use the z-test for proportions?

np ≥ 5 and nq ≥ 5

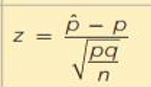
What parameter is tested using this?

Proportion (p)

What test statistic is used when σ is unknown?

t-test

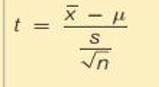
What are the requirements to use the t-distribution for means?

Population is normal or sample size n>30

What is the sampling distribution when σ is unknown?

t-distribution

What test statistic is used when σ is known?

z-test

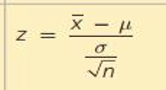
What are the requirements to use the z-distribution for means?

Population is normal or sample size n>30

What is the sampling distribution when σ is known?

Normal (z)

What test statistic is used to test variance?

Chi-square test

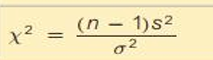
What are the requirements to use the chi-square test?

Population must be strictly normal

What is the sampling distribution for variance?

Chi-square (χ²)

test statistic

a score that tells you how far your sample is from what you'd expect if the null hypothesis were true

critical value method

determines whether to reject the null hypothesis by comparing the test statistic to a critical value.

critical region (rejection region)

the area corresponding to all values of the test statistic that cause us to reject the null hypothesis

critical values

the specific points that define boundaries for the critical region in hypothesis testing.

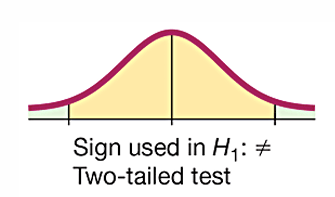
for a two-tailed test, the critical region is in

the two extreme regions (tails) under the curve

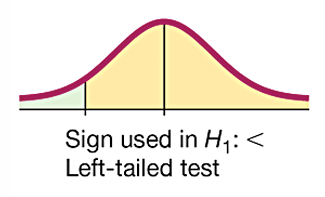
for a left-tailed test the critical region is in

the extreme left region (tail) under the curve

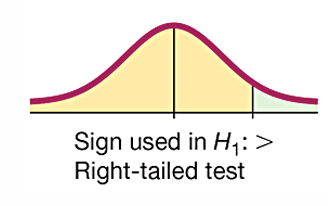
for a right-tailed test the critical region is in

the extreme right region (tail) under the curve.

P-value method

make a decision by comparing the P-value to the significance level

P-value

the probability of observing a test statistic as extreme as the one observed, assuming the null hypothesis is true.

p

population proportion

p̂

sample proportion

if a P-value is > α

fail to reject H₀

is P-value is ≤ α

reject H₀

type I error

rejecting H₀ when it is true

type II error

failing to reject H₀ when it is false

conditions for a binomial distribution 

• There is a fixed number of trials.

• The trials are independent.

• Each trial has two categories of “success” and “failure.”

• The probability of a success remains the same in all trials.

the Student t-distribution has a mean of

t=0

The standard deviation of the Student t distribution

varies with the sample size and is greater than 1

As the sample size n gets larger, the Student t distribution ____________

gets closer to the standard normal distribution.

all values of X² are

nonnegative and follow a chi-squared distribution. (not symmetric)

there is a different X² distribution for

each degree of freedom.

p̄

Pooled Sample Proportion (combines two sample proportions into one)

Pooled sample requirements

samples are from two simple random samples, samples are independent, at least 5 successes and 5 failures in each sample

when is a two tailed test used?

when the claim states that the two proportions are different (but deos not specify which is larger)

what test is used for this claim?

H0: p1 = p2​

H1: p1 ≠ p2 

Two-tailed test

when is a right-tailed test used?

when the claim states that one proportion is greater than another

what test is used for this claim?

H0: p1 = p2 ​

H1: p1 > p2

Right-tailed test

when is a left-tailed test used?

when the claim states that one proportion is less than another

what test is used for this claim?

H0: p1 = p2​ 

H1: p1 < p2

left tailed test

when the p-value is less than the significance level, we ___

reject the null hypothesis.

when the p-value is greater than the significance level, we ___

fail to reject the null hypothesis.

d̅

represents the mean difference between paired samples in hypothesis testing.

d

individual difference between the two values in a single matched pair

s_1²

larger of the two sample variances

F-distribution

the dsitribution of the ratio of two sample variances

properties of F-distribution

skewed right (not symmetric), always positive, shape depends on degrees of freedom

if σ₁²=σ₂² (null hypothesis), then F≈ ?

1

when F is larger, that means the

sample variances differ a lot