Function and graph

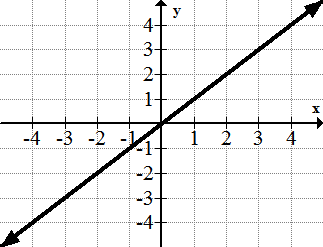
The identify function ,f(x) = x

The simplest function and all straight lines are transformations of the identity function family. 

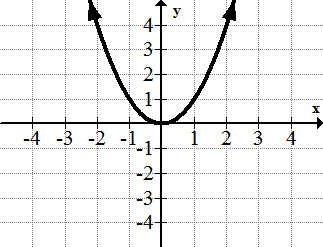
The squaring Function: f(x) = x² (parabola)

(quadratic function) is commonly called a parabola and is useful for modeling the motion of falling objects. All parabolas are transformations of this squaring function. 

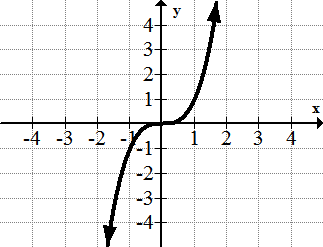
The cubing function: f(x) = x³

A different kind of symmetry than the squaring function. Since volume is measured in cubic units, many physics applications use the cubic function

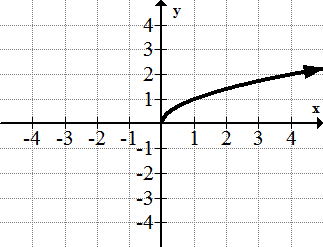
Square root function: f(x) = x^1/2

The square root function is not defined over all real numbers. It introduces the possibility of complex numbers and is also closely related to the squaring function. 

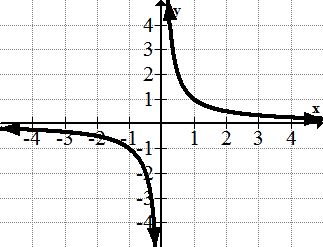
The reciprocal function : f(x) = x^-1 or 1/x

The reciprocal function is also known as a hyperbola and a rational function. It has two parts that are disconnected and is not defined at zero.

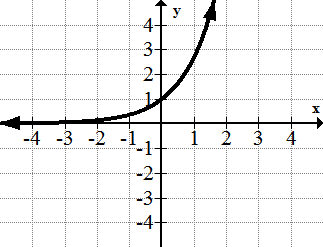
The exponential Function: f(x) = e^x

one of the first functions you see where  is not the base of the exponent. This function eventually grows much faster than any power function.

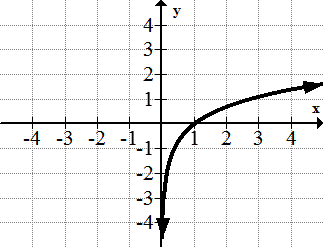
The logarithm Function: f(x) = ln(x)

closely related to the exponential function family. Many people confuse the graph of the log function with the square root function. Careful analysis shows several important differences.

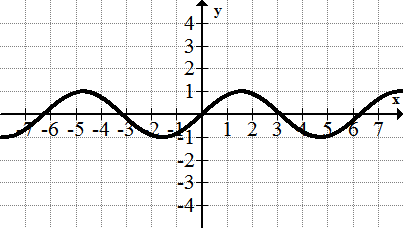
The Periodic Function: f(x) = sin(x)

The sine graph is one of many periodic functions. Periodic refers to the fact that the sine wave repeats a cycle for every period of time.

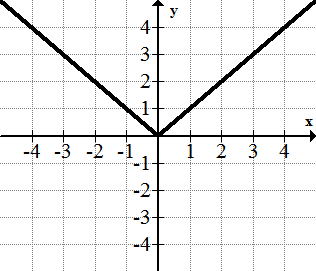
The absolute Value Function: f(x) = |x|

The absolute value function is one of the few basic functions that is not totally smooth.

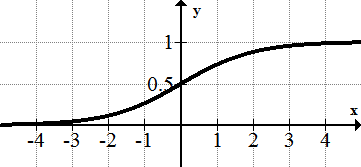
The logistic Function: f(x) = 1/1+(e^-x)

a combination of the exponential function and the reciprocal function.

A function

a rule that takes any input  and gives a specific output. When you use letters like f,g,h, or j to describe the rule, this is called function notation.

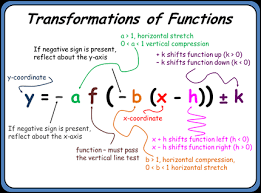
Transforming a function

You can multiply the ‘x’ by a constant and/or add a constant to the ‘x’. Example: f(x-2) or f(bx + c)

function notation

A transformation can be written in this and in point notation.

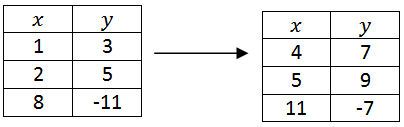
Point notation

it takes each coordinate  and assigns a new coordinate based on the transformation.