ACT Math Formulas and Terms

Formulas and Terms that will make the ACT Math portion go quicker.

𝑥ᵐ × 𝑥ⁿ =

𝑥ᵐ⁺ⁿ

ⁿ√ab =

ⁿ√a × ⁿ√b

(𝑎ⁿ)ᵐ =

𝑎⁽ⁿᵐ⁾

Quadratic vertex form

With vertex (h,k)

𝑦 = 𝑎(𝑥 − ℎ)² + 𝑘

If |𝑎| > 1 → The parabola is narrower (stretched vertically)

If 0 < |𝑎| < 1 → The parabola is wider (compressed vertically)

Percent Change Formula

[(New - Old) / Old] x 100%

log(a) + log(b) =

log(ab)

log(x) - log(y) =

log(x/y)

Area of a parallelogram

A = bh

Area of a trapezoid

A = ½ (b₁+b₂) x h

Area of a triangle

A = ½bh

Area of a cube

A = 6𝑠²

Volume of a cube

𝑣 = 𝑠³

Volume of a rectangular prism

V = lwh

Volume of a cylinder

𝑣 = π𝑟²h

Volume of a sphere

V = (4/3)π𝑟³

Mean

Average

Median

Middle number

Mode

Most frequent number

Isosceles triangle definition

at least 2 equal sides

Equilateral triangle definition

3 equal sides

Area of a circle

A = πr²

Circumference of a circle

C = 2πr

Arc length of a circle

s = rθ

θ in radians

Sector area of a circle

A = ½ r² θ

θ in radians

Equation for a circle

(x - h)² + (y - k)² = r²

(h,k) = vertex

Arithmetic sequence for the nth term

a_n = a₁ + (n−1) x d

Arithmetic Series

[n x (a₁ + a_n)] / 2

Geometric sequence nth term

a_n = a₁ x rⁿ⁻¹

Sequence and Series definition

Sequence = set of numbers that follow a pattern

Series = sum of the terms in a sequence

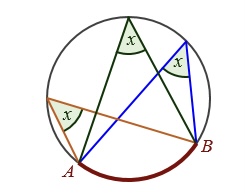
Angles ended by points A and B on a circle are:

Congruent

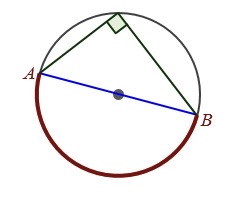
Angles that are ended by points A and B (AB = diameter) are:

90 degrees

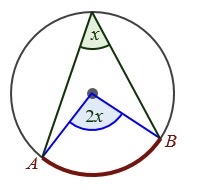
The central angle is how many times as big as an angle on the circle that are ended with the same arc?

2 times

Geometric Series

S_n = [a(1-r^n)] / (1-r)

Basic Probability Formula

P(event) = desired outcomes/total outcomes

Probability of “at least 1”

P(at least one) = 1 - P(none)

Ex)

Probability of rolling a 6 at least once on two die rolls = 1 - P(no sixes) = 1 - (5/6 × 5/6) = 11/36

If one event has m outcomes and second event has n outcomes, what are the total outcomes?

m x n

Probability Combinations Formula

(n!) / [r! (n - r)!]

n = Total group

r = Chosen from group

Ex)

Choosing 2 students from a group of 5:

5! / 2!3! = 10

Sine and cosine amplitude

a in y = a sin(x)

Period definition

The length of one full cycle

Period of sine and cosine

[2 x (pi)] / b

B in the equation y = sin(Bx)

Period of tangent

(pi) / b

B in the equation y = tan(Bx)

Frequency of a trig graph

1 / period

Ellipse equation

[x²/a²] + [y²/b²] = 1

a = radius in x direction

b = radius in y direction

y-3 = 3 UP

Equation for the foci of an ellipse

f² = a² - b²

Hyperbola Equation

[x²/a²] - [y²/b²] = 1 (left/right)

OR

[y²/b²] - [x²/a²] = 1 (up/down)

y-6 = up 6 units

Asymptote of hyperbola

± b/a (x)

LR x =/ 0

UD y =/ 0

Foci of a hyperbola

f² = a² + b²

Inscribed angle definition

All endpoints lie on the circle circumference

Degree measure of an arc

The angle of its central angle (ends of the arc connected to the center) or 2 times its inscribed angle

Sine and cosine graph

Sine starts at (0,0)

Cosine starts at (0,1)

Cofunction Identity

Cos(90°-x) = sin x

Law of sines

Sin A / a = Sin B / b = Sin C / c

Use when you know one side and two angles or

You know 2 sides and an angle opposite to one of the sides

Law of cosines

c² = a² + b² - 2ab(cosC)

Use when you know 3 sides

Or

2 sides and their included angle

ALWAYS RATIONALISE ANSWER

Not a question. Just a reminder

i in the denominator

Multiply by conjugate

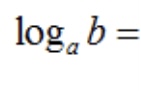
Look at the picture

Look at the picture

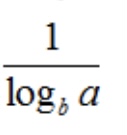
Vertex of a quadratic in standard form

-b/2a = x-coordinate of vertex

Discriminant of a quadratic of standard form

-b² - 4ac

0 = touches x-axis once

+ = intersects x-axis twice

- = never intersects x-axis

Area of an ellipse

A = πab

1 of 2 with exclusive events probability

P(a) + P(b)

Both of two related events probability

P(a)•P(b/a)

Both of two independent events probability

P(a)•P(b)

Mutually exclusive definition

Can’t be true at the same time

How many unique arrangements for the entirety of one group?

x!

Permutation Formula

P = (n!) / (n-r)!

n = total

r = taken from total / group size

1 of 2 with dependent events probability

P(A or B) = P(A) + P(B) - P(A and B)

What counts as a valid probability model

All probabilities for a situation add to 1

All probabilities are positive

Combination Formula

C = n! / [k!(n-k)!]

n = total

k = how many in the group

Combination vs Permutation

Combination = order doesn’t matter

Permutation = order matters

Matrix definition

An array of values

Adding matrices

Add corresponding numbers in corresponding positions

Multiplying matrices condition

Number of columns in 1st matrix = Number of rows in 2nd matrix

The product of two matrixes has

Same number of columns as rows in 1st matrix

Same number of rows as columns in 2nd matrix

Multiplying matrices with multiple columns/rows

1) add product of r1m1 • c1m2

2) add product of r1m1 • c2m2

3) add product of r2m1 • c1m2

4) add product of r2m1 • c2m2

r = row c = column

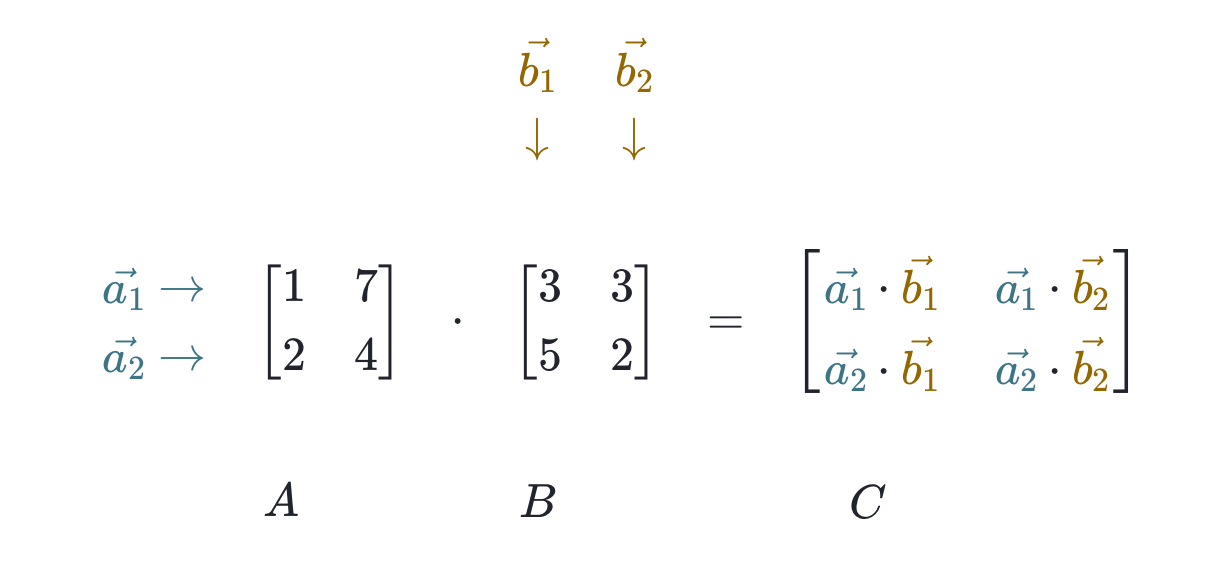
Determinant of a 2-row 2-column matrix

ad-bc

ab

cd

Exterior angle

Supplementary to interior angle and proportional to the opposite side

“Interior angle measure“

Sum of the interior angles

Sum of interior angles of a polygon

(n-2)180°

n = sides

Area of a rhombus

A = ½ d₁d₂

d = diagonals

Area of a parallelogram

A = bh

Compound Interest Formula

Picture from Google

Surface Area of a cylinder

2(pi)r(r+h)

Expected probability value

The sum of the products of the probability and the amounts

x • P(x)

Fundamental Counting Principle

N ways to do one thing and m ways to do another, combination = n • m ways to do both

Equilateral triangle area

A = (root 3) / 4 [s²]

Number of diagonals in a polygon?

n(n-3) / 2