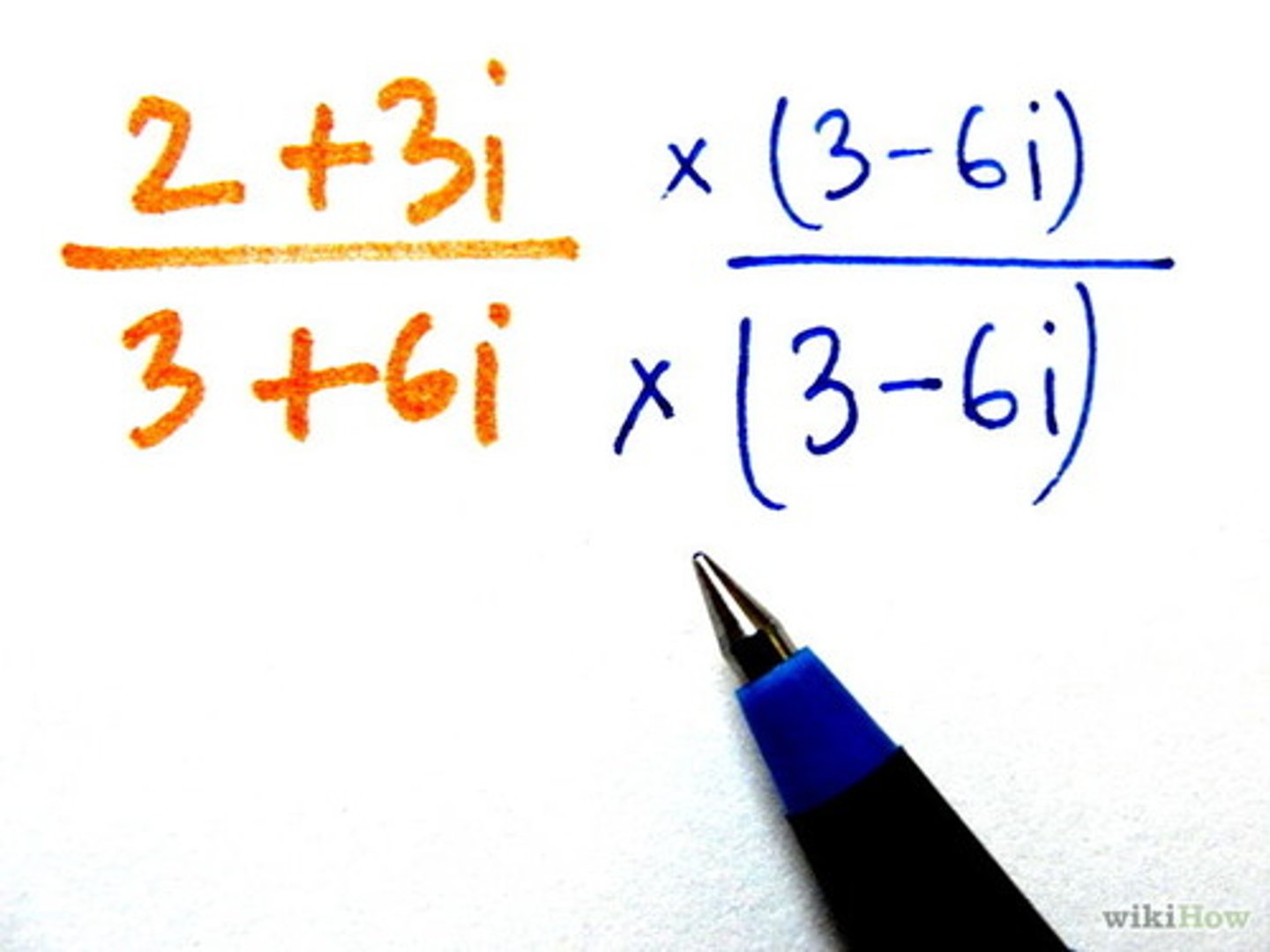1.3, 1.4 Quadratic Equations & Complex Numbers

quadratic equation

an equation of the standard form ax² + bx + c = 0, where a ≠ 0

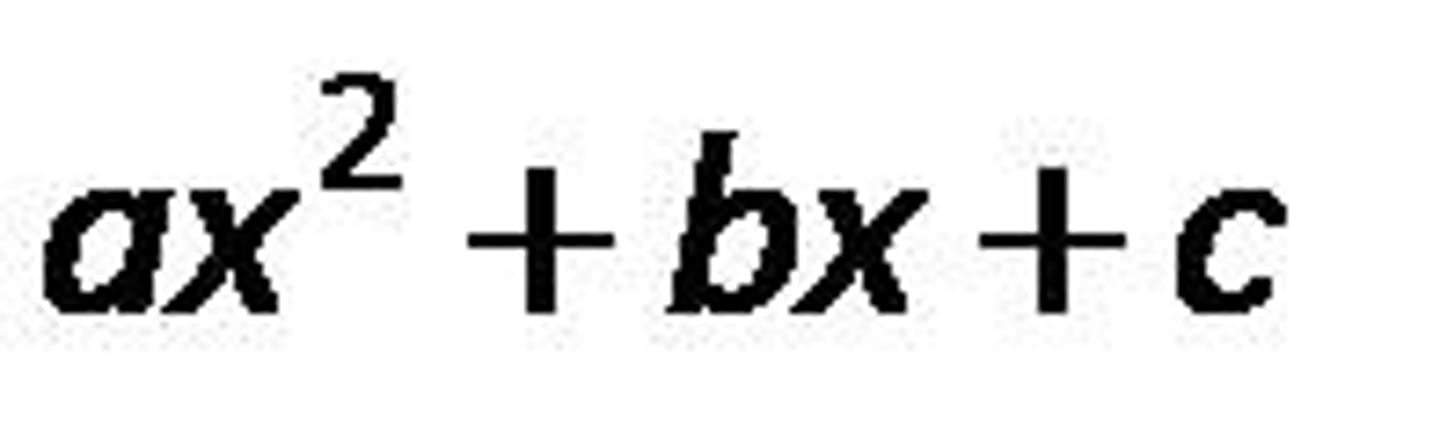
quadratic formula

[-b ± √(b² - 4ac)] / (2a)

is used as a form of solving quadratic equations

4 ways to solve quadratic equations

4 ways: factoring, square root property, completing the square, quadratic formula

factoring is based on

the zero product property. review P4.2, P4.3

to factor, put polynomial in standard form, factor and get linear factors, set each linear factor to 0 and solve

completing the square

using a trinomial in standard form:

1. subtract c

2. divide by a on both sides

3. add the square of 1/2 the coefficient of x

4. write the left hand side as a perfect square

5. solve using the square root property

square root property

for any number n ≥ 0, if x² = n, then x = ±√n.

To solve a quadratic equation in the form x^2=n, take the square root of each side.

can be generalized to cube roots and higher powers

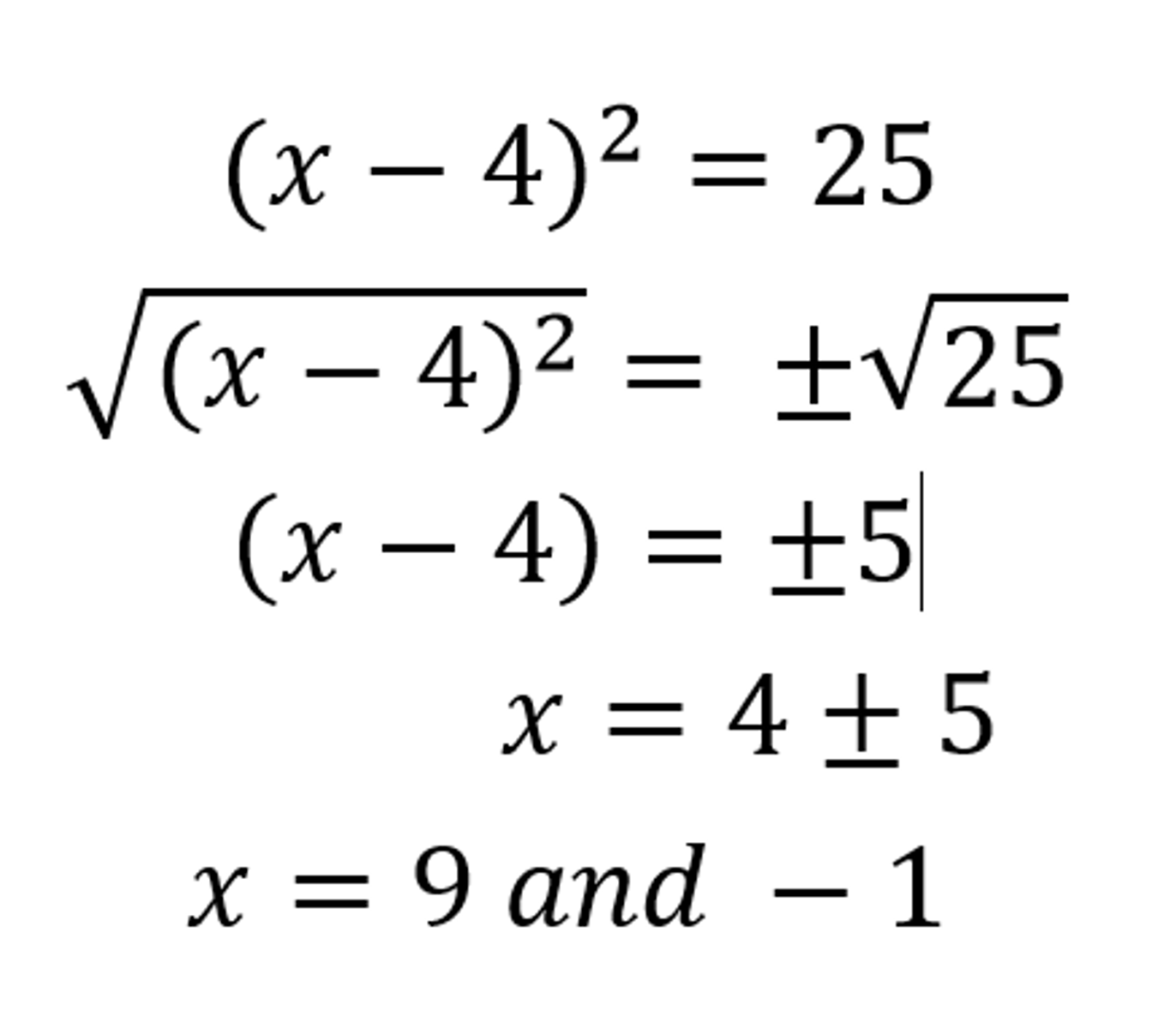
using the quadratic formula

1. make sure the trinomial is in standard form

2. plug a,b,c into the formula and solve

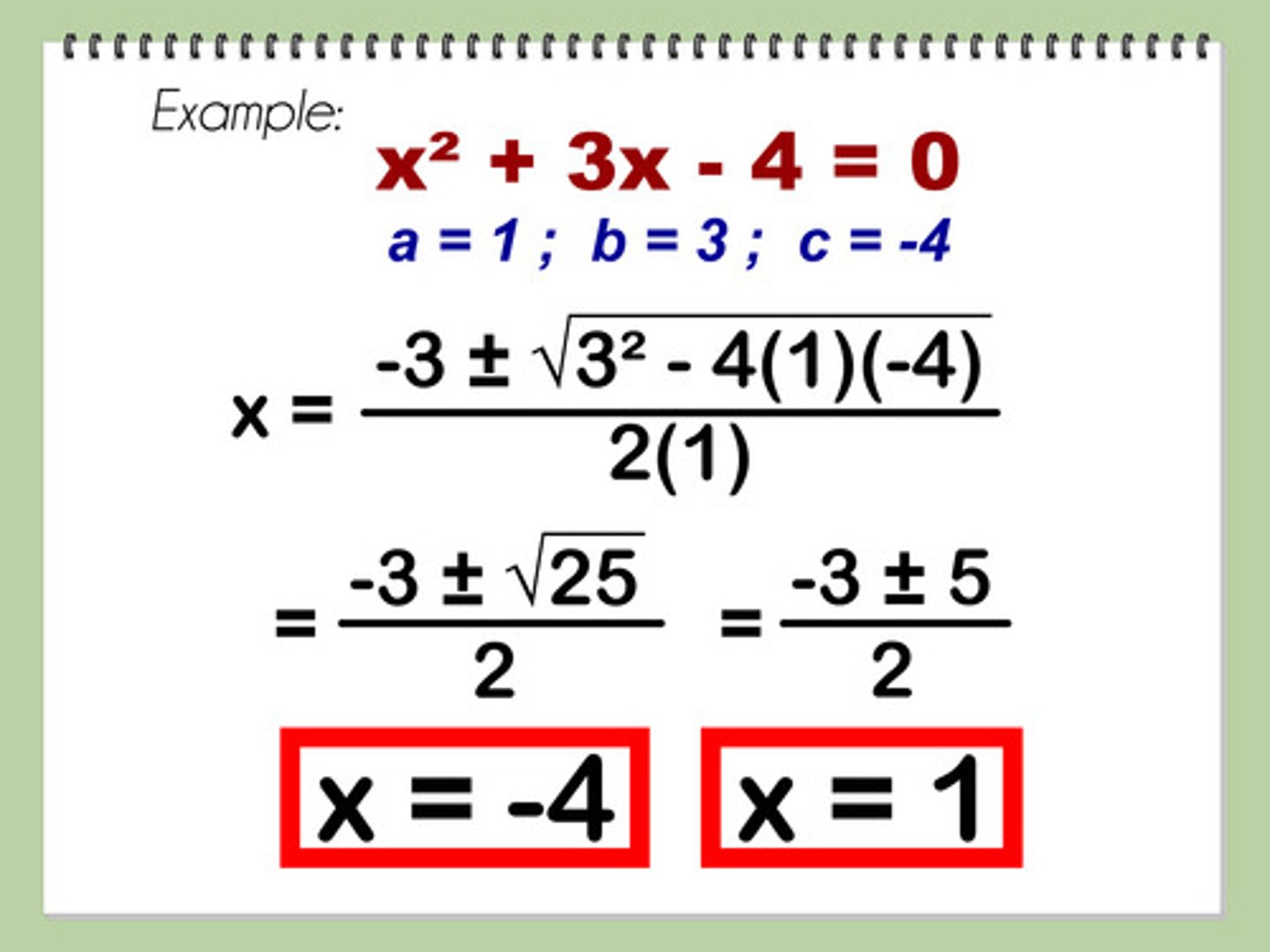
what is the discriminant

The discriminant of the quadratic equation ax^2+bx+c=0 is

D=b^2-4ac

If D>0, then the equation has two distinct real solutions

if D=0, then the equation has exactly one real solution

if D<0, then the equation has no real solution

imaginary numbers

Square roots of negative numbers. Have no points on the number line

uses most of the rules of radicals: refer to P.6

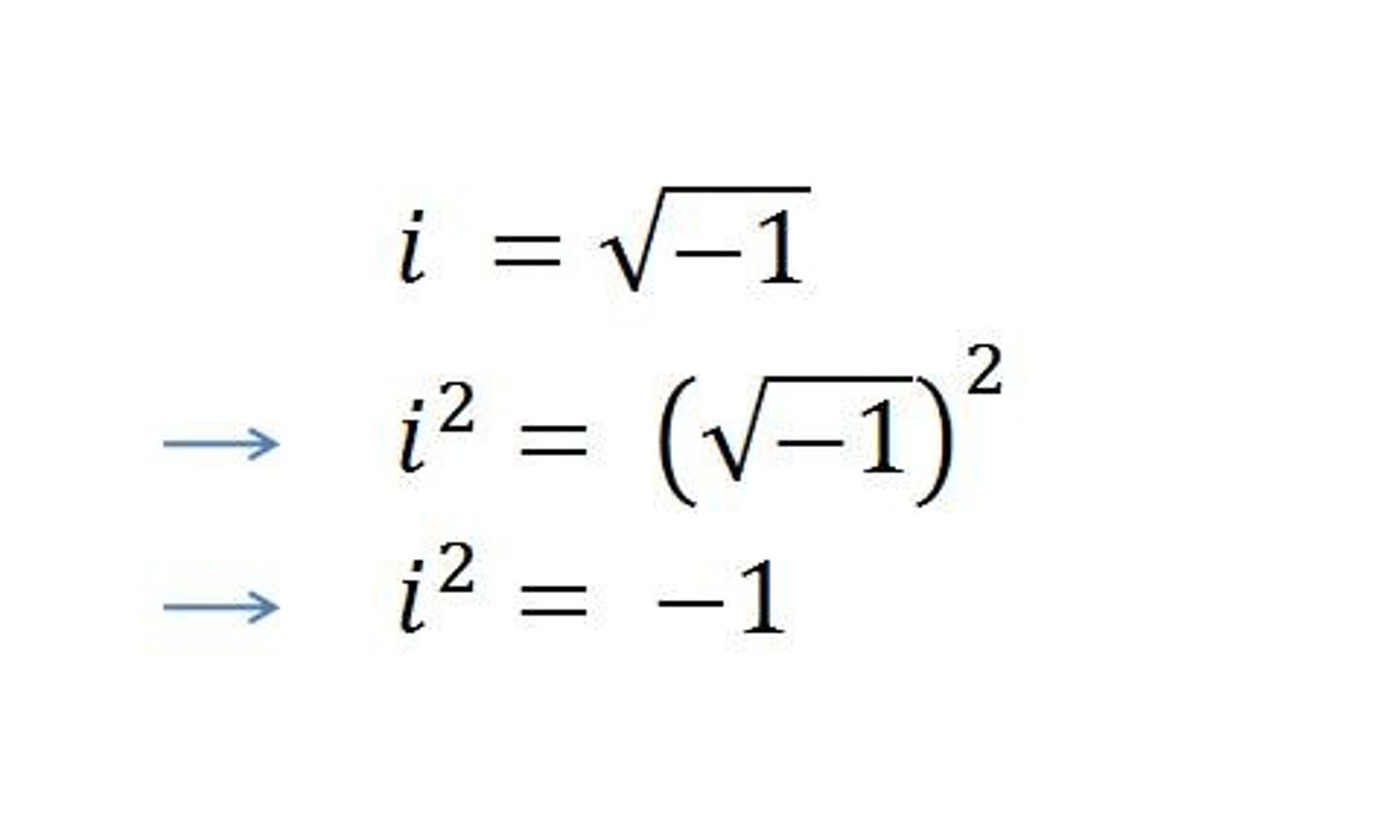
i =

√-1

i²=

-1

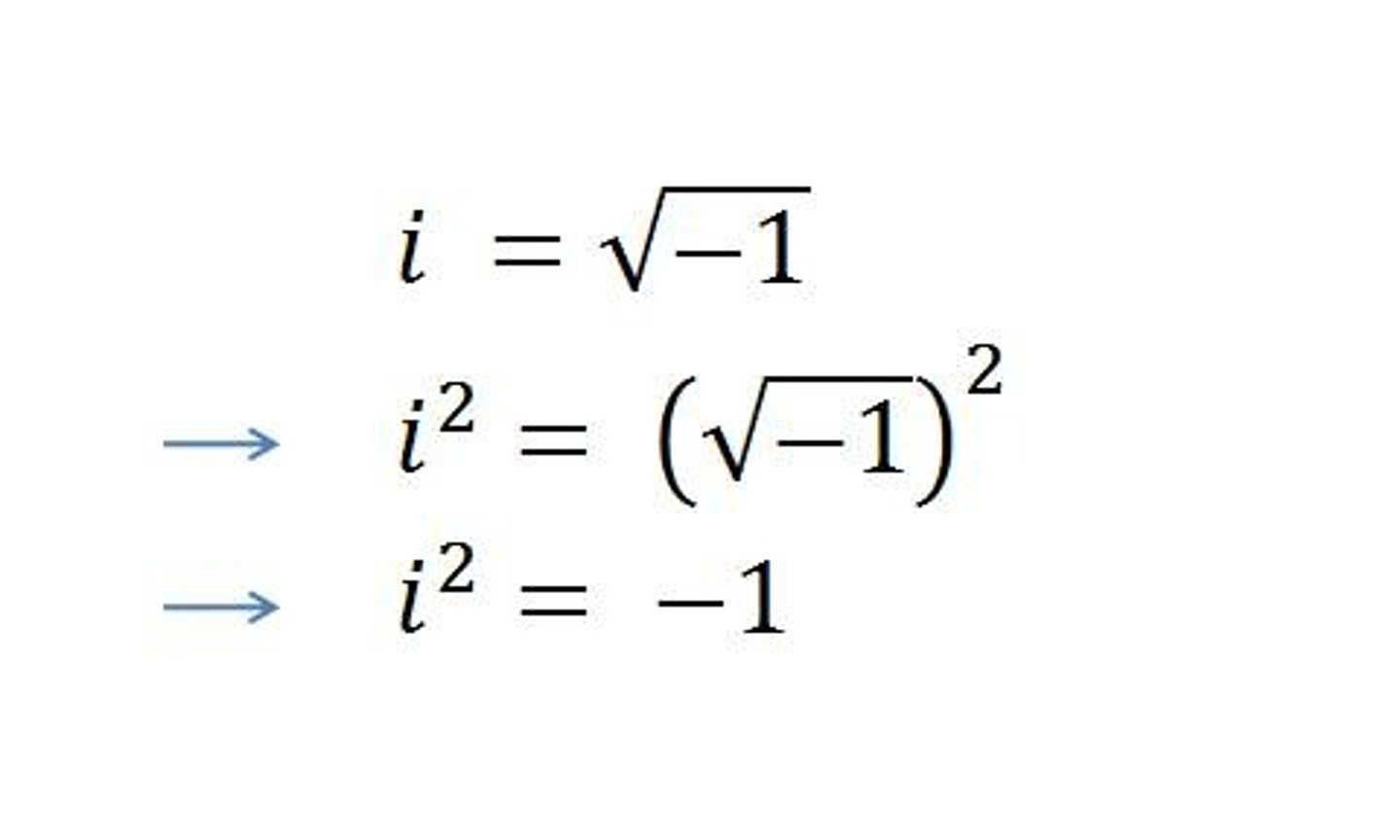
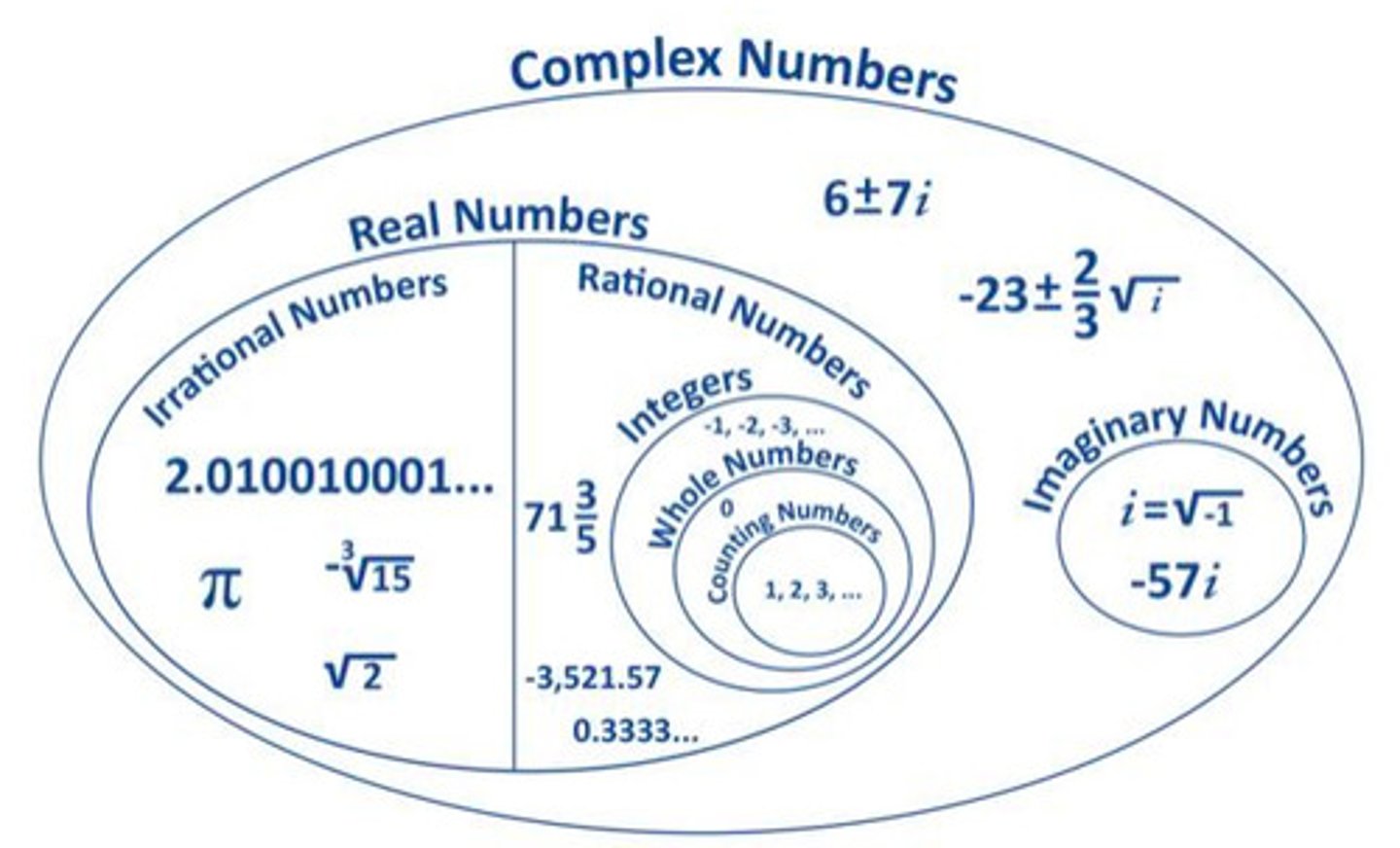
complex numbers

has a standard form: z=a+bi, a is a real number

imaginary numbers and rational numbers

rational, irrational, and imaginary numbers do not overlap but can be added/subtracted/multiplied/divided together

adding/substracting complex numbers

(a+bi)+(c+di) = (a+c) + (b+d)i

Add real parts, then add the imaginary parts on, expressing the sum as a complex number

multiplying complex numbers

1. FOIL (refer to P4.1)

2. Simplify *WHENEVER IT IS i^2 REPLACE with -1*

3. Write answer in standard form (a+bi)

Ex: -2i(5+31)

-10i-6i^2

-10i-6(-1)

-10+6

6-10i

dividing complex numbers

1. multiply the numerator and denominator by the conjugate of the denominator

2. solve accordingly

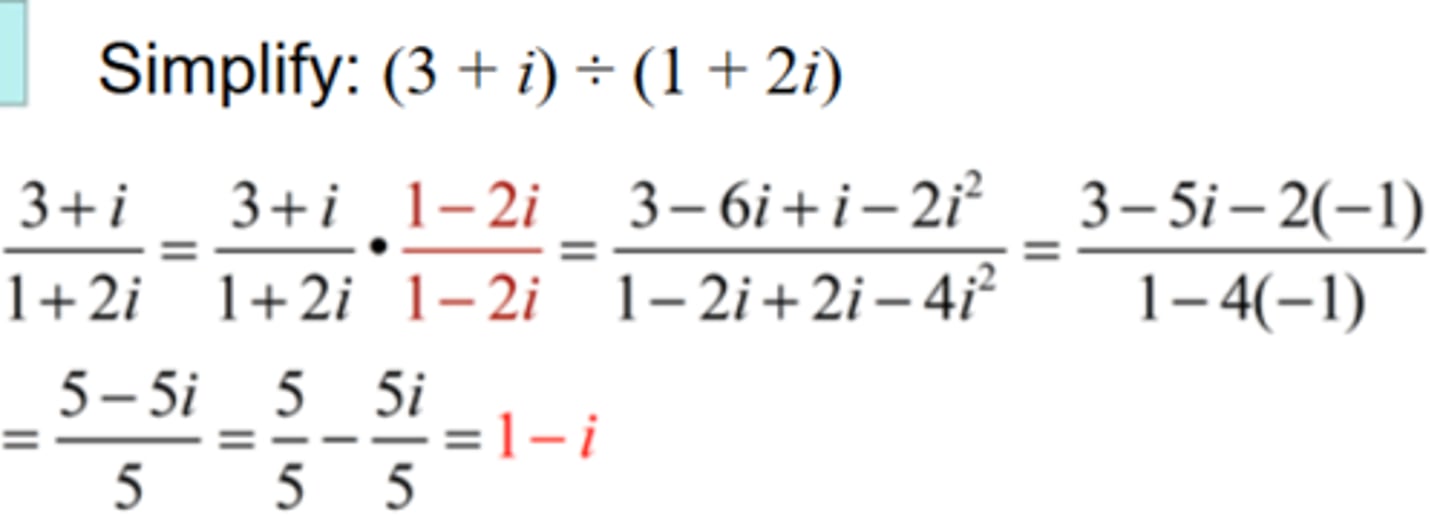
conjugate of the denominator

The same to terms with the opposite sign between the two terms, the real term does not change signs.

Remember to replace i^2 with a = -1, combine like terms, and then continue simplifying the fraction.

(is similar to rationalizing the denomator; the number is always rational: refer to P3.1,P3.2)