114 MATH FINAL EXAM REVIEW
1/16
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
17 Terms

Consider the following table of values
(a) Find limt→3−f(t)
This limit approaches from the left (values less than 3). Since t≤3 in this case, we use the first part of the function:
limt→3−f(t)=1+3=4
(b) Find limt→3+f(t)
This limit approaches from the right (values greater than 3). Since t>3 in this case, we use the second part of the function:
limt→3+f(t)=6−3=3
(c) Find limt→3f(t)
For the overall limit to exist, both one-sided limits must be equal. Since:
limt→3−f(t)=4
limt→3+f(t)=3
The limits are not equal, so:
limt→3f(t) does not exist.
(d) Find f(3)
Since 3≤3, we use the first part of the function:
f(3)=1+3=4
Summary of Results:
(a) limt→3−f(t)=4
(b) limt→3+f(t)=3
(c) limt→3f(t) does not exist
(d) f(3)=4
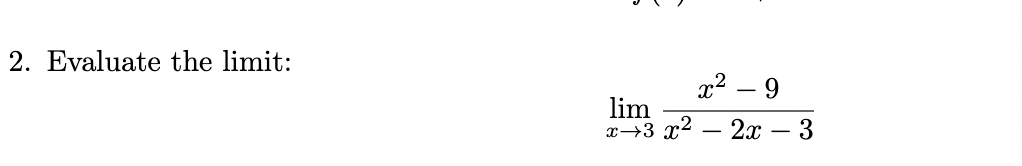
Evaluate the limit
a.) Plug the limit number into the equation.
b.) if it equals 0/0, simply it.
Factor the Numerator:
The numerator x^2−9 is a difference of squares: x2−9=(x−3)(x+3)
Factor the Denominator:
The denominator x2−2x−3 can be factored by finding two numbers that multiply to −3 and add to −2: x2−2x−3=(x−3)(x+1)
c.) Rewrite the limit and cancel common factors.
d.) Substitute the limit into the equation again.
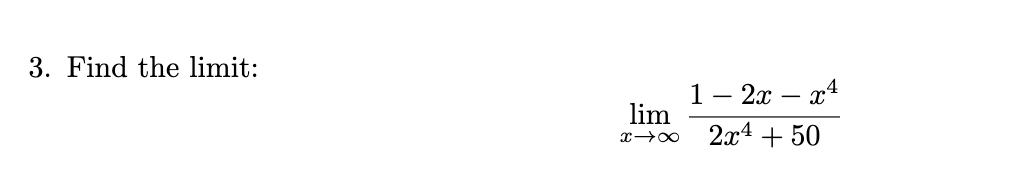
Find the limit
a.) Identify the highest degree terms
In both the numerator and the denominator, identify the terms with the highest degree as x→∞.
Numerator: The highest degree term is −x^4.
Denominator: The highest degree term is 2x^4.
b.) Factor Out the Highest Degree Terms
Factor out x^4 from both the numerator and the denominator:
1−2x−x42x4+50=x4(1x4−2x3−1)x4(2+50x4).2x4+501−2x−x4=x4(2+x450)x4(x41−x32−1).
c.) Simply the expression by canceling x^4, 2+x450x41−x32−1/2+50/x4
d.) Evaluate the Limit
As x→∞:
1x^4→0x41→0
2x^3→0x32→0
50x^4→0x450→0
Thus, the limit simplifies to:
0−0−12+0=−12.2+00−0−1=2−1.
(-1/2)
![<p><span>ind the average rate of change of the function f (x) = x^2/2 over the interval [4, 8].</span></p>](https://knowt-user-attachments.s3.amazonaws.com/97f89061-4471-457c-b297-6df7d266f258.png)
ind the average rate of change of the function f (x) = x^2/2 over the interval [4, 8].
Step 1: Identify the Formula for Average Rate of Change
The average rate of change of a function f(x)f(x) over the interval [a,b][a,b] is given by the formula:
Average Rate of Change=f(b)−f(a)/ b−a.
Step 2: Define a and b. In this case, a = 4 and b = 8.
Step 3: Calculate f(a) and f(b) by plugging it into the original equation.
f(4)=4^2/2=16/2=8.
f(8) = 8²/2 = 64/2 = 32
Step 4: Put it into the equation of the average rate of rate (the new values). f(8) - f(4) / 8-4 = 32-8/8-4 = 24/4 = 6. THE ANSWER IS 6.
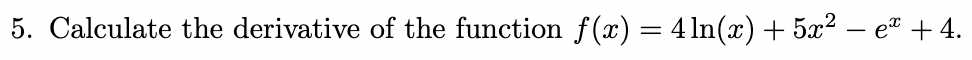
Calculate the derivative of the function
Step 1: Differentiate each term
Differentiate 4ln(x): derivative of ln(x) is 1/x, so 4 × 1/x = 4/x
Differentiate 5x25x2:
The derivative of x^n is nx^n-1
Therefore, the derivative of 5x² is 5 × 2x²-1 = 10x
Differentiate −e^x:
The derivative of e^x is e^x.
Therefore, the derivative of −e^x is -e^x
Differentiate the constant 4:
The derivative of a constant is 0.
Therefore, the derivative of 4 is 0.
Step 2: Combine the Derivatives
f’(x) = 4/x +10x -e^x + 0…. the final answer is 4/x+10x-e^x

Calculate the derivative of this function
Quotient rule is used ( f(x) = g(x) / h(x) ) to f’(x) = g’(x)h(x) - g(x)h’(x) divided by (h(x))²
Step 1: Identify g(x) and h(x)
-g(x) = e^x
-h(x) = x² + 4
Step 2: Calculate g’(x) and h’(x)
-Derivative of e^x = e^x
-Derivative of x² + 4 = 2x
Step 3: Apply Quotient Rule by substituting g(x), g’(x), h(x), and h’(x) into the quotient rule formula.
f(x) = g(x) / h(x) ) to f’(x) = g’(x)h(x) - g(x)h’(x) divided by (h(x))²
e^x (x² + 4) - e^x (2x)/ (x² +4)²

Calculate the derivative of the function
We will use the chain rule. The chain rule states that if you have a composite function y=ln(u)y=ln(u), where u=x4+1u=x4+1, then the derivative is given by: dy/dx = 1/u x du/dx
Step 1: Identify u; u = x^4 + 1
Step 2: Differentiate u du/dx = d/dx (x^4 + 1) = 4x³
Step 3: Apply the Chain Rule ( dy/dx = 1/u x du/dx)
Substitute in u and du/dx ( 1/x^4 +1 times 4x³ )
Step 4: Write the final expression dy/dx = 4x³ / x^4 + 1
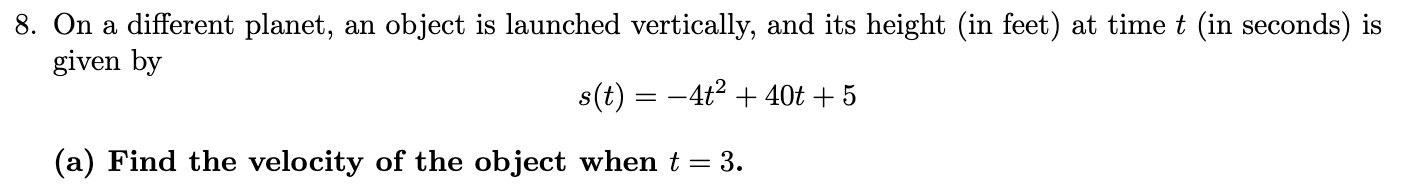
On a different planet, an object is launched vertically, and its height (in feet) at time t (in seconds) is given by…
a.) Find the velocity of the object when t=3.
b.) Find the acceleration of the object when t=3.
a.) To find the velocity of the object when t=3t=3 seconds, we need to calculate the derivative of the height function s(t) with respect to time t. The velocity v(t) is given by the derivative s′(t).
-Step 1: Write the height function, s(t) = d/dt (-4t² +40t +5)
-Step 2: Differentiate s(t)
-4t² derivative is -8t.
40t derivative is 40.
5 derivative is 0.
SO, it’s now s’(t) = -8t + 40
-Step 3: Evaluate s’(t) at t=3 by substituting 3 into the derivative to find the velocity.
s’(3) = -8(3)+40
s’(3) = -24 + 40 = 16… ANSWER IS 16.
b.) Step 1: Differentiate s’(t) to find the acceleration. s’’(t)
-8t derivative is -8.
derivative of 40 is 0. So the equation is -8.
Step 2: Evaluate s’’(t) at t=3.
Since the second derivative s′′(t)is a constant, it does not depend on t. Therefore, the acceleration is:
s′′(3)=−8… ANSWER IS -8

If f ′′(0) = 2, what must be true?
(a) f is concave up at x = 0
(b) f is concave down at x = 0
(c) f has an inflection point at x = 0
(d) f is increasing at x = 0
Second Derivative Test: The second derivative f′′(x) provides information about the concavity of the function f(x):
If f′′(x)>0, the function is concave up at that point.
If f′′(x)<0, the function is concave down at that point.
If f′′(x)=0, it may indicate a possible inflection point, but further analysis is needed.
(a) f is concave up at x=0
Since f′′(0)=2 (which is greater than 0), this means that the function is concave up at x=0.
This statement is true
(b) f is concave down at x=0
Since f′′(0)=2 (which is greater than 0), this means that the function is not concave down at x=0.
This statement is false.
(c) ff has an inflection point at x=0.
An inflection point occurs where the concavity changes, which typically happens when f′′(x)=0 or is undefined. Since f′′(0)=2 and does not change sign around x=0, we cannot conclude that there is an inflection point at this location.
This statement is false.
(d) f is increasing at x=0
The second derivative does not provide direct information about whether the function is increasing or decreasing. To determine if f is increasing, we would need to know the first derivative f′(0). Therefore, we cannot conclude that f is increasing at ( x = 0 \ based solely on ( f''(0) ).
This statement is false.
a is the right answer.
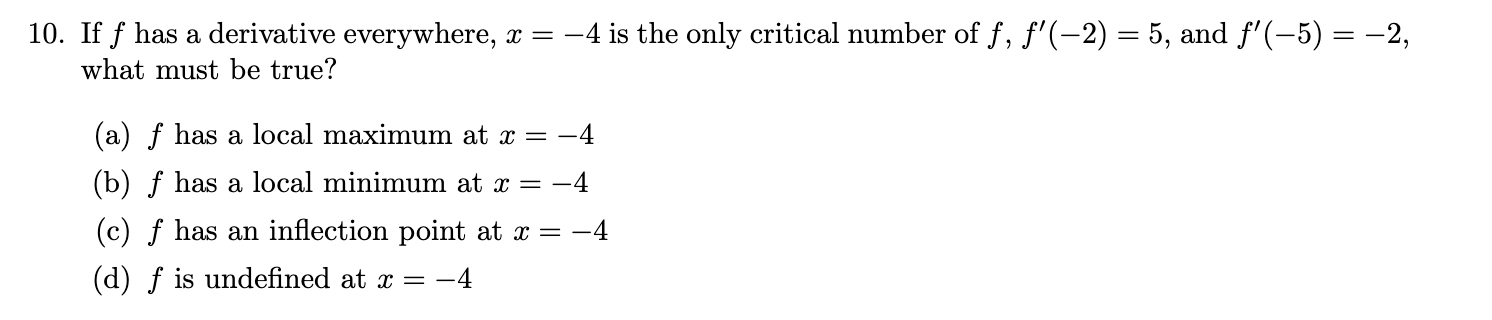
If f has a derivative everywhere, x = −4 is the only critical number of f , f ′(−2) = 5, and f ′(−5) = −2,
what must be true?
(a) f has a local maximum at x = −4
(b) f has a local minimum at x = −4
(c) f has an inflection point at x = −4
(d) f is undefined at x = −4
Critical Number: A point cc in the domain of ff where f′(c)=0 or f′ is undefined.
Local Maximum: A point where f changes from increasing to decreasing.
Local Minimum: A point where f changes from decreasing to increasing.
Inflection Point: A point where the concavity of the function changes, which is determined by the second derivative f′′(x).
1. Understanding the Critical Number at x=−4:
Since x=−4is the only critical number, we know that f′(−4)=0 because it cannot be undefined since ff has a derivative everywhere).
2. Behavior of f′′Around x=−4:
To determine whether x=−4 is a local maximum or minimum, we need to analyze the behavior of f′ around this point.
We know f′(−5)=−2 (which is negative), indicating that ff is decreasing at x=−5.
We also know f′(−2)=5 (which is positive), indicating that f is increasing at x=−2.
Since f′ changes from negative to zero at x=−4 and then to positive, this indicates that f is decreasing before x=−4 and increasing after x=−4. Therefore, x=−4 is a local minimum.
Evaluating Each Option:(a) f has a local maximum at x=−4
False: We determined that x=−4 is a local minimum, not a maximum.
(b) f has a local minimum at x=−4
True: As analyzed, x=−4 is indeed a local minimum.
(c) f has an inflection point at x=−4
False: We do not have information about the second derivative f′′(x) to conclude that there is an inflection point at x=−4.
(d) f is undefined at x=−4
False: The problem states that f has a derivative everywhere, so f must be defined at x=−4.
B is the correct answer, f has a local minimum at x=−4.
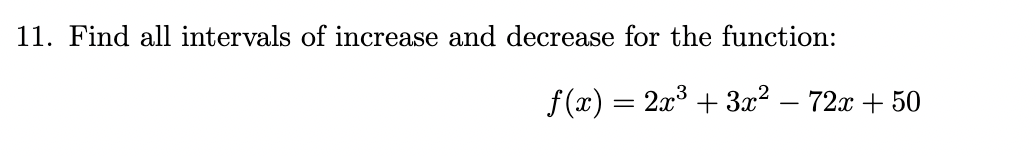
Find all intervals of increase and decrease for the function
Step 1: Find the First Derivative
The first step is to find the derivative of the function, f′(x). Use Power Rule.
2x³ derivative is 6x²
3x² derivative is 6x
-72x derivative is 72.
50 is 0.
Step 2: Set the First Derivative to Zero
To find the critical points, we set f′(x)=0f:
6x^2+6x−72=0
Dividing the entire equation by 6 simplifies it:
x^2+x−12=0
Step 3: Factor the Quadratic
Next, we factor the quadratic equation:
(x+4)(x−3)=0 to get critical points.
Step 4: Test Intervals Around the Critical Points
We will test the intervals determined by the critical points x=−4 and x=3:
Intervals: (−∞,−4), (−4,3), (3,∞)
Choose test points from each interval:
For x=−5 (in (−∞,−4)): f(−5)=6(−5)2+6(−5)−72=150−30−72=48(positive)f′
For x=0 (in (−4,3): f′(0)=6(0)2+6(0)−72=−72(negative)
For x=4(in (3,∞): f′(4)=6(4)2+6(4)−72=96+24−72=48(positive)
Step 5: Determine Intervals of Increase and Decrease
From the test results:
Interval (−∞,−4): f′>0 → Increasing
Interval (−4,3): f′<0 → Decreasing
Interval (3,∞): f′>0→ Increasing
The intervals of increase and decrease for the function f(x) are:
Increasing: (−∞,−4) and (3,∞)
Decreasing: (−4,3)
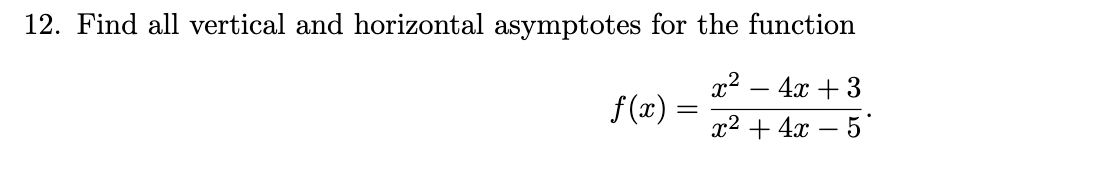
Find all vertical and horizontal asymptotes for the function
Step 1: Find Vertical Asymptotes
Vertical asymptotes occur where the denominator is zero (and the numerator is not zero at those points).
Set the denominator to zero: x^2+4x−5=0
Factor the quadratic: To factor, we look for two numbers that multiply to −5 and add to 4. The factors are 5 and −1 :
(x+5)(x−1)=0
Thus, vertical asymptotes are at x= 5 and x=1.
Step 2: Find Horizontal Asymptotes
Horizontal asymptotes are determined by the degrees of the numerator and denominator.
Identify the degrees:
The degree of the numerator x2−4x+3 is 2.
The degree of the denominator x2+4x−5 is also 2.
Compare the degrees: Since the degrees of the numerator and denominator are equal, the horizontal asymptote can be found by taking the ratio of the leading coefficients. So, leading coefficient of numerator divided by leading coefficient of denomiator = 1/1 = 1.
Vertical Asymptotes: x = -5 (x=1 is a root of both the numerator and denominator, it is a removable discontinuity), horizontal: y=1
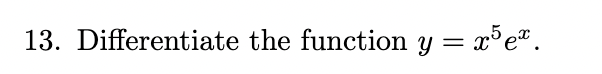
Differentiate the function
Product rule: (uv)’ = u’v + uv’
Step 1: Identify u and v
u = x^5
v = e^x
Step 2: Differentiate u and v.
x^5 derivative is 5x^4
e^x derivative is e^x
Step 3: Apply product rule
y’ = (5x^4)(e^x) + (x^5)(e^x)
Step 4: Factor out common term, e^x
y’ = e^x(5x^4)+(x^5)
Step 5: Simplify
y’ = e^x(5x^4 + x^5) = e^xx^4 (5+x)
y’ = e^xx^4 (5+x)
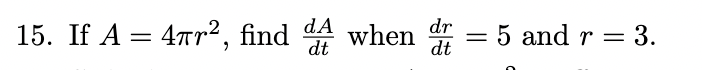
If A = 4πr2, find dA/dt when dr/dt = 5 and r = 3.
Step 1: Differentiate A with respect to t.
dA/dt = Aπd/dt(r²)
Step 2: Apply the Chain Rule
d/dt (r²) = 2r dr/dt
^ Substitute above back into equation
dA/dt = 4π(2r dr/dt)
Which simplifies to: dA/dt = 8πr dr/dt
Step 3: Substitute the given values
dr/dt = 5
r = 3
dA/dt = 8π(3) (5) = 120π