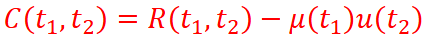Probability Test 4

The likelihood function, L(θ), is the n-dimensional density function thought of as a function of θ with x1, x2, through xn as known parameters:

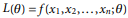
For many densities, it is more convenient to consider the log-likelihood function, l(θ):

l(θ) = logL(θ)

Computing the MLE consists of the following steps:

1. Compute the likelihood function.

2. If it appears beneficial, compute the log-likelihood function.

3. Differentiate the likelihood or log-likelihood function with respect to θ, set the derivative to 0, and solve for θˆ. If θ consists of multiple components, differentiate separately with respect to each component, and solve the set of equations.

A random process is WSS if it satisfies two conditions:

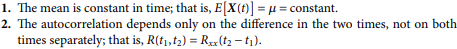
The likelihood ratio is the ratio of densities:

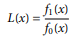
For many densities, however, it is more convenient to compute the log-likelihood ratio:

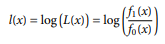
Pr[True Positive] =

Pr[False Positive] =

Pr[True Negative] =

Pr[False Negative] =

Also,

TP: Sensitivity

FP: Type I Error

TN: Specificity

FN: Type 2 Error

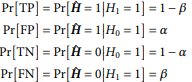
RADAR

null hypothesis =

alternative hypothesis =

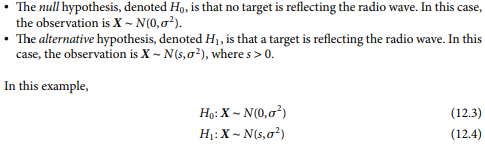
PDF of interarrival times of Poisson Process?

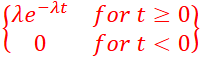
MAP Test

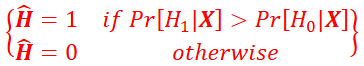
How many dimensions does X(t) have?

What are they?

2

Time and ensemble

Two conditions of WSS?

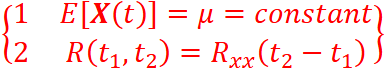
For WSS process, at what argument is autocorrelation maximum?

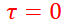
What does random vector x =?

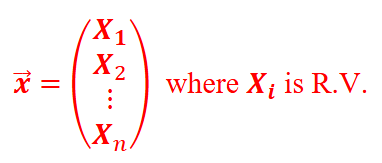
If a random process X(t) has a Gaussian PDF of N(10,1), is it WSS?

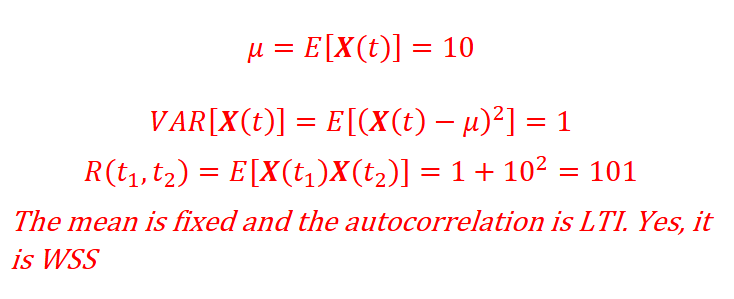
X(n) is Markov

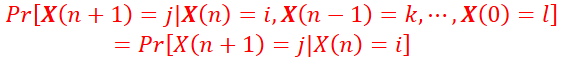
A Markov chain is homogeneous

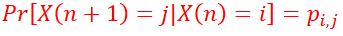
If a stationary random process X(t) has a Gaussian PDF of N(10,1), what is its mean, variance, autocovariance, and autocorrelation.

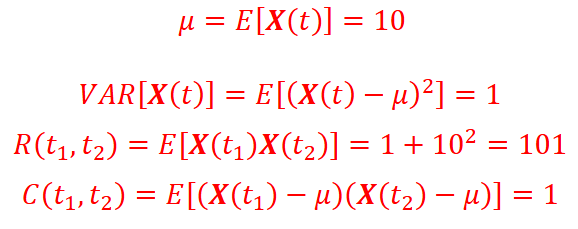
How is the Autocovariance of X(t) calculated?

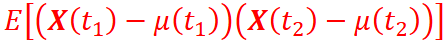
How is the Autocorrelation of X(t) calculated?

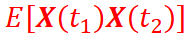
What is the mathematical relationship between Autocorrelation and
Autocovariance?