Statistics Chapter 13 Probability Rules

What is the multiplication rule for independent events?

P(A and B) = P(A) * P(B)

What is "P( getting heads when flipping a coin and rolling a six on a die ) = P(heads) * P(rolling a six on a die)" an example of?

The multiplication rule for independent events

What is "P(A and B) = P(A)*P(B)"?

The multiplication rule for independent events

What is the general addition rule?

P(A or B) = P(A) + P(B) - P(A and B)

Why do we subject P(A and B) in the general addition rule?

This is so we do not include the cross section of the events happening in our final probability

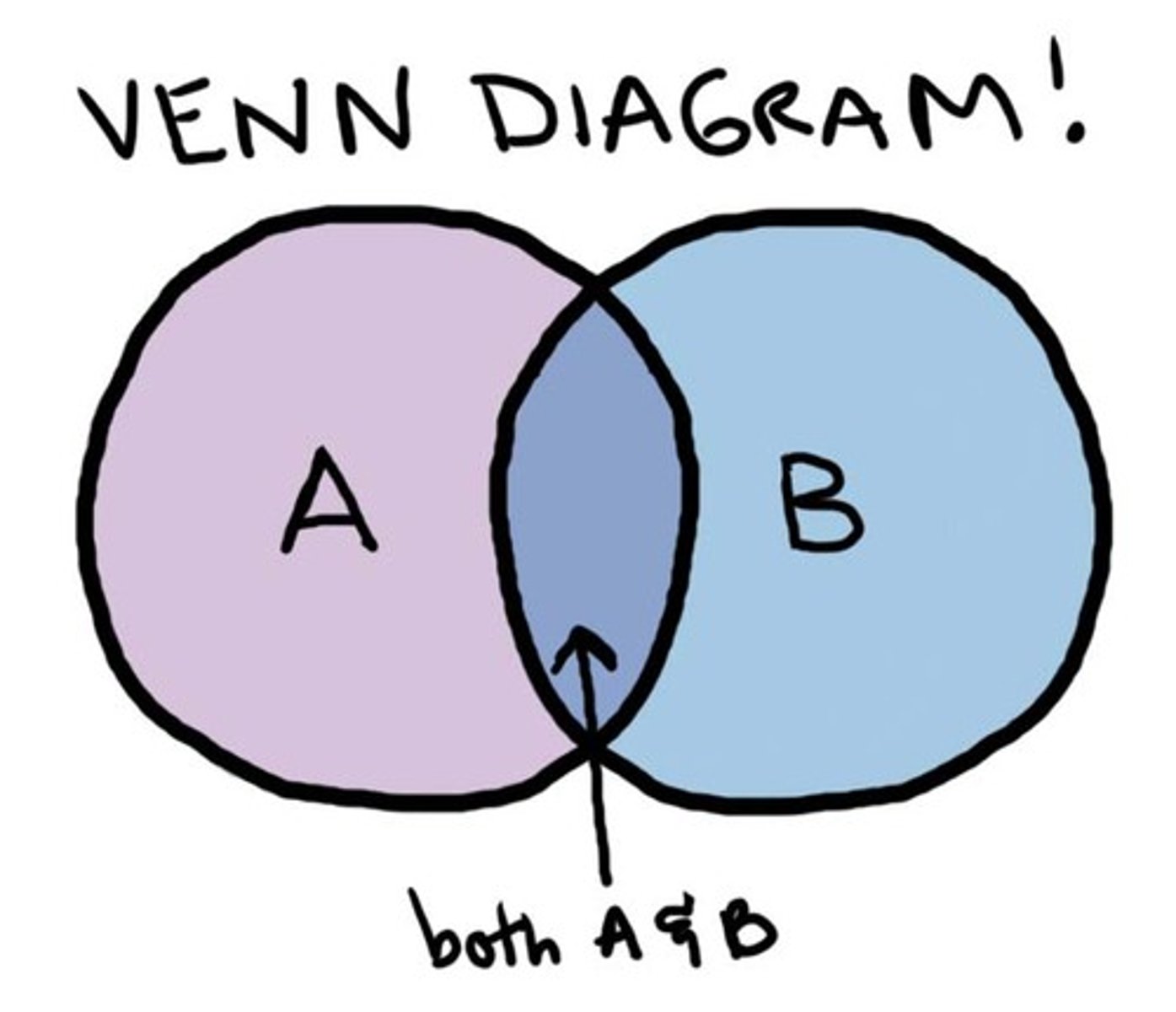
What is " P(A or B) = P(A) + P(B) - P(A and B)" an example of?

The general addition rule

What is P(heart or ace) = P(ace) + P(heart) -P(ace and heart) an example of?

General addition rule

What is conditional probability?

Probability of one event happening changes when we know a condition of a separate event

What is the rule of conditional probability?

P(B|A)=P(A and B)/P(A)

What is the general multiplication rule for ALL events? (We can use this rule when we are not sure if events are independent?)

P(A and B) = P(A)*P(B|A)

What is P(ace and heart) = P(ace)*P(heart | ace) an example of?

General multiplication rule?

If we are looking to solve the chance of two students not solving a math problem given that they are independently working on it, what would we do?

Find the chance of them both not solving the problem by using P(not solving) = 1- P(solving). Once we obtain those two values, we can multiply them together P(student 1 not solving)*P(student two not solving) =P(both not solving). We can do this because we know they are independent. If we did not know, we would use the general multiplication rule.

If we wanted to know what are the chances we draw both an ace and a spade, what would we do?

P( ace and spade) = P(ace) * P(spade | ace)

How do we find the probability that something does not happen?

P(event not happening) = 1-P(event happening)