CS301 Studying

CS301

Q: What are the two types of statistics?

A: Descriptive statistics and inferential statistics.

Q: What is descriptive statistics?

A: It uses data to describe a population through numerical calculations, graphs, or tables (e.g., maximum, average, minimum).

Q: What is inferential statistics?

A: It makes inferences or predictions about a population based on a sample of data from that population.

Q: What is a key purpose of descriptive statistics?

A: Representation of data.

Q: What are the two main types of data?

A: Numerical data and categorical data.

Q: What are the two types of numerical data?

A: Continuous and discrete.

Q: What are the two types of categorical data?

A: Nominal and ordinal.

Q: What is continuous data?

A: Numerical data that can take any value within a range.

Q: What is discrete data?

A: Numerical data that takes specific, countable values.

Q: What is nominal data?

A: Categorical data with no inherent order.

Q: What is ordinal data?

A: Categorical data with a meaningful order or ranking.

Q: Give examples of nominal data.

A: Gender (Female, Male), Languages (English, French, Spanish).

Q: Give an example of ordinal data.

A: Educational background: 1 - Elementary, 2 - High School, 3 - Undergraduate, 4 - Graduate.

Q: What is discrete numerical data?

A: Numeric values that can only take certain distinct, countable numbers, such as integers.

Q: Give examples of discrete data.

A: Number of children in a family (0, 1, 2…), number of cars sold per day, shoe sizes (6, 6.5, 7).

Q: Give examples of continuous data.

A: Weight (52.3 kg, 52.35 kg…), Distance (3.2 miles, 3.25 miles…), Speed (60.5 mph, 60.55 mph…).

Q: What are the types of numerical data?

A: Discrete, continuous, interval, and ratio.

Q: What is interval data?

A: Continuous data measured along a scale with equal intervals between values, but with no true zero.

Q: Can ratios be meaningfully calculated with interval data?

A: No, ratios are not meaningful with interval data.

Q: Can addition and subtraction be meaningfully performed on interval data?

A: Yes, addition and subtraction are meaningful.

Q: Give an example of interval data.

A: Temperature in Celsius (0°C does not mean no temperature, and 20°C is not twice as hot as 10°C).

Q: What is ratio data?

A: Continuous data measured along a scale with equal intervals and a true zero.

Q: Can ratios be meaningfully calculated with ratio data?

A: Yes, ratios are meaningful (e.g., 20 kg is twice 10 kg).

Q: Give examples of ratio data.

A: Height, Weight (0 kg means no weight).

Q: What is an outlier? How is it Detected?

A: An extreme value in a dataset compared to all other values.Values more than 1.5×IQR above Q3 or below Q1 are considered outliers, where IQR = Q3 − Q1.

Q: Given the exam scores [40, 87, 88, 90, 95], which score is the outlier?

40

Q: What visualizations can help detect outliers?

A: Boxplots, scatter plots, and histograms.

Q: What impact can outliers have on data analysis?

A: They can distort means, standard deviations, regression models, etc., but sometimes contain important information (e.g., fraud detection, rare diseases).

Q: What does central tendency indicate in a dataset? What are the common measures of central tendency?

A: It tells the location or center of the data. Mean, Median, and Mode.

Q: What is the formula for the mean?

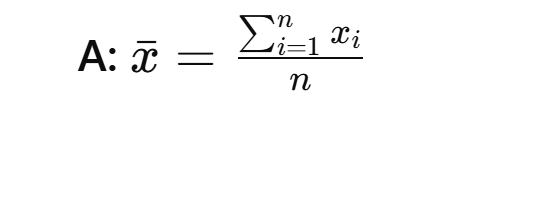
Q: What is the formula for the median? Is it affected by outliers?

A:

• If n is odd: Median = value at position (n+1)/2(n+1)/2(n+1)/2 in the ordered dataset

• If n is even: Median = average of values at positions n/2n/2n/2 and (n/2)+1(n/2)+1(n/2)+1 in the ordered dataset
  A: No, the median is robust to outliers.

Q: What is the mode of a dataset and its properties?

A: The mode is the value that occurs most often in a dataset. It is not affected by outliers. A dataset can have one mode, multiple modes, or no mode.

Example: For the dataset [2, 2, 3, 7, 18, 18, 18, 18, 23, 23, 23, 31, 40], the mode is 18.

Q: When is each measure of central tendency most appropriate?

A:

• Mean: Good for datasets without outliers.

• Median: Good for datasets with or without outliers.

• Mode: Good for categorical data.

What is the formula for Variance? What is Variance’s Main Function?

Q: What is a population in statistics?

A: A collection of individuals, objects, or events whose properties are to be analyzed.

Q: What is a sample in statistics?

A: A subset of a population; a well-chosen sample contains most of the information about a particular population parameter.

Q: Why do data scientists often use sample variance instead of population variance?

A: Because they mostly deal with sample data rather than the entire population.

Q: How does sample variance generally compare to population variance?

A: Sample variance is usually greater than population variance.

Q: Why is the sample variance formula divided by n−1n-1n−1 instead of nnn?

A: Dividing by n−1n-1n−1 compensates for the lack of information about the population.

Q: Why is standard deviation used instead of variance?

A: Because variance values are often too large for visualization or comparison, so standard deviation provides a more interpretable measure.

Standard Deviation Formula

Q: What is the coefficient of variation (CV)?

A: It is a measure of the dispersion of data relative to its mean.

Q: When is the coefficient of variation useful?

A: When comparing the variability of two datasets.

Q: What does a smaller CV indicate?

A: The data is more stable and consistent, and the sample mean is a more precise estimate of the population mean.

Coefficient of Variation

Q: What is covariance?

A: It measures the directional relationship between two variables.

Q: What are the three types of covariance?

A:

• Zero covariance: No relationship between the variables.

• Positive covariance: If one variable increases, the other also increases.

• Negative covariance: If one variable increases, the other decreases.

Q: Does covariance have a fixed range?

A: No, it can be any positive or negative number; the sign shows direction, and the magnitude depends on the data scale.

Covariance Formula?

Sample Covariance has n-1 as the denominator

Population Covariance is just N

Q: What is correlation? What is the range? What does the values mean?

A: It measures the strength of the relationship between two variables, building on covariance which shows the direction. From −1 to +1. +1 is Perfect positive correlation (when X increases, Y always increases). −1 indicate Perfect negative correlation (when X increases, Y always decreases). r=0 indicate No linear relationship between the variables.

Q: What is the formula for correlation?

A: r = cov(X, Y) / (σ²ₓ · σ²ᵧ)

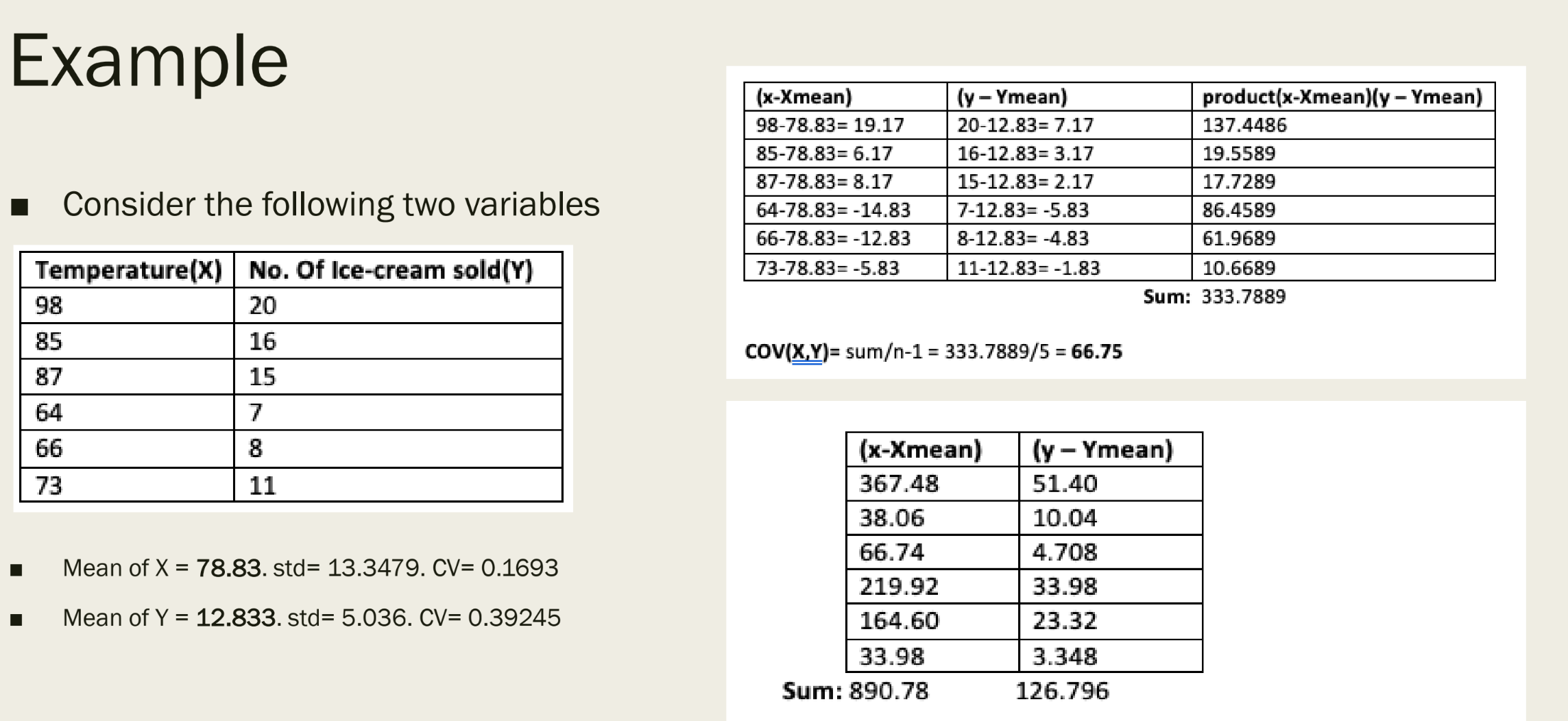
Calculate the Covariance of this dataset

Q: What is inferential statistics?

A: A branch of statistics that allows conclusions or predictions about a population based on a sample.

Q: What are the two ways to collect data?

A: Collect all the data or collect a sample from the data.

Q: What are the two main categories of sampling techniques?

A: Probability sampling and non-probability sampling.

Q: What are probability sampling techniques?

A: Random sampling, stratified sampling, and systematic sampling.

Q: Why is non-probability sampling considered less reliable?

A: Because it may introduce bias since not everyone in the population has a chance to be selected, even though it is easier and cheaper.

Q: What is simple random sampling?

A: A probability sampling technique where each individual has an equal chance of being selected.

Q: What is stratified sampling?

A: A probability sampling method where the population is divided into subgroups (strata) based on characteristics, and a random sample is taken from each group to ensure representation.

Q: What is systematic sampling?

A: A probability sampling technique where every k-th element is selected from a list after a random starting point.

Q: Give an example of systematic sampling.

A: Starting at student #1 in a class roster and then selecting students #6, #11, #16, #21, and #26.

Q: What is a normal distribution?

A: A probability distribution also known as the Gaussian distribution, characterized by a bell-shaped curve where the mean, median, and mode are equal.

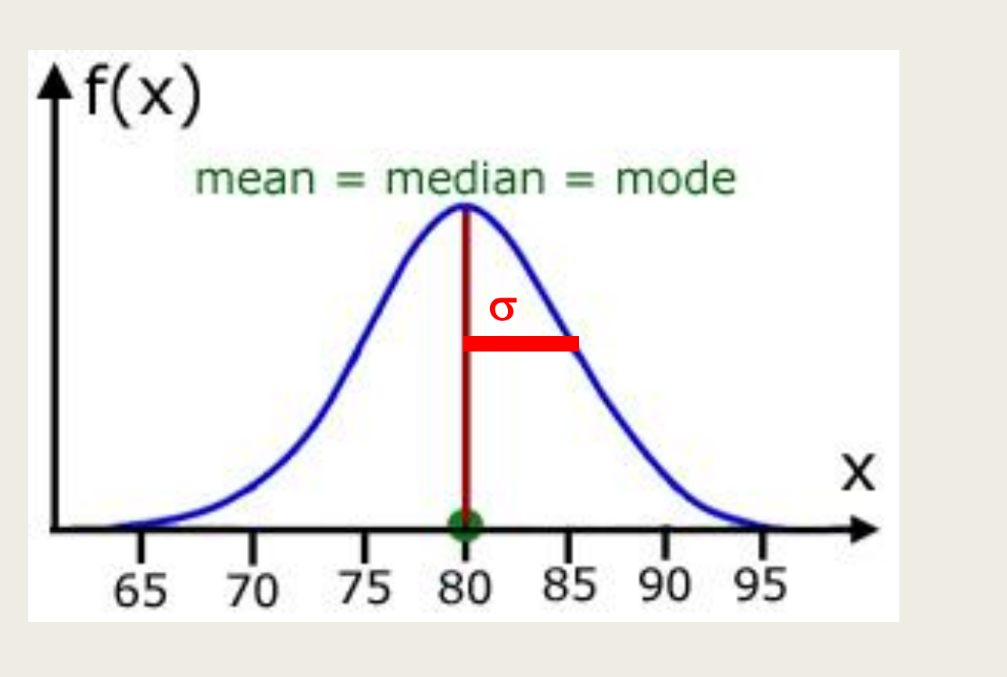
Q: What is the standard normal distribution?

A: A normal distribution with a mean of 0 and a standard deviation of 1.

Q: What is a Z-score?

A: A standardized value that represents how many standard deviations a data point is from the mean, calculated as

Q: What is skewness?

A: A measure of asymmetry (imbalance) of a data distribution around the mean.

Q: What does it mean when data is skewed?

A: Data values are concentrated on one side of the distribution.

Q: What is positive (right) skewness?

A: A distribution with a long tail on the right side where extreme values are larger; Mean > Median > Mode.

Q: What is negative (left) skewness?

A: A distribution with a long tail on the left side where extreme values are smaller; Mean < Median < Mode.

Q: What is the difference between a population and a sample?

A: A population is the entire group of interest, while a sample is a smaller subset drawn from the population.

Q: Why are sample statistics commonly used in practice?

A: Because they are more convenient and practical than measuring the entire population.

Q: What does the Central Limit Theorem (CLT) state?

A: If many random samples of size n ≥ 30 are taken from any population, the sampling distribution of the sample mean will be approximately normal, regardless of the population’s distribution.

Q: How does the Central Limit Theorem apply in practice?

A: Even if the population distribution is skewed, the distribution of sample means from many samples of size 30 will be approximately normal.

Q: What happens to the average of sample means under the CLT?

A: It will be very close to the true population mean.

Q: Why is the Central Limit Theorem important for statistical methods?

A: Many tools (z-scores, t-tests, confidence intervals, hypothesis testing) assume normality, which is satisfied by the sampling distribution of the mean.

Q: Why is a sample size of n ≥ 30 commonly used in the CLT?

A: It is small enough to be practical and large enough for the CLT to usually hold.

Q: What does pandas do?

A: Pandas is a Python library used for data manipulation and analysis, providing tools to work with structured data such as tables (DataFrames), including cleaning, transforming, and analyzing data.

Q: What is correlation analysis used for?

A: It helps determine the relationship between numerical features.

Q: When should a feature be removed based on correlation?

A: If two features have high correlation (> 0.8), one may be redundant and should be removed; if a feature has low correlation with the target (< 0.1), it may not be useful.

Q: What is machine learning?

A: Machine learning is the science of getting computers to act without being explicitly programmed; it enables computers to learn from existing data to forecast future behaviors, outcomes, and trends.

Q: What are the general steps in a machine learning workflow?

A:

1. Problem Definition and Understanding

2. Data Collection

3. Data Preprocessing

4. Data Exploration and Visualization

5. Data Splitting

6. Model Selection

7. Model Training

8. Model Evaluation

9. Model Interpretation (Optional)

10. Deployment (Optional)

11. Documentation and Reporting

12. Continuous Improvement

Q: What is the difference between the traditional (rule-based) approach and the machine learning approach?

A:

• Rule-based approach: Explicitly programmed to solve problems; decision rules are clearly defined by humans.

• Machine learning approach: Trained from examples; decision rules are complex, fuzzy, and learned from data rather than defined by humans.

Q: What is the key summary of machine learning?

A:

• Machine learning uses historical data to make predictions.

• Unlike data mining, which discovers unknown patterns, machine learning applies previously learned knowledge to new data for real-life decision-making.

• Computers approximate complex functions from historical data.

• Decision rules are not explicitly programmed but learned from data.

Q: How do you determine if you need machine learning for a business problem?

A: Consider if you need to automate the task. Tasks that are high-volume, involve complex rules, or deal with unstructured data are good candidates.

Q: Give an example of a task suitable for machine learning.

A: Sentiment analysis of web reviews, which involves a high volume of unstructured text and complex human language.

Q: How do you formulate a business problem for machine learning?

A: Clearly define what you want to predict given which input, following the pattern: “given X, predict Y.”

Q: In sentiment analysis, what is the input and output?

A:

• Input: Customer review text

• Output: Sentiment (positive, negative, neutral)

Q: Why is having sufficient examples important for machine learning?

A: Machine learning always requires data; generally, the more examples, the better the model’s performance.

Q: What are the two parts each example must contain in supervised learning?

A:

• Features: Attributes of the example

• Label: The answer you want to predict

Q: Give an example in sentiment analysis.

A: Thousands of customer reviews (features) with ratings or sentiment labels (positive, negative, neutral).

Q: Why is it important for a machine learning problem to have regular patterns?

A: Machine learning learns regularities and patterns; it struggles to learn rare or irregular patterns.

Q: Give an example related to sentiment analysis.

A: Positive words like “good,” “awesome,” or “love it” appear more often in highly-rated reviews, while negative words like “bad,” “lousy,” or “disappointed” appear more often in poorly-rated reviews.

Q: Why is finding meaningful representations of data important in machine learning?

A: Machine learning algorithms operate on numbers, so examples must be represented as feature vectors; good features often determine the success of the model.

Q: Give an example of data representation in sentiment analysis.

A: Represent a customer review as a vector of word frequencies, with the label being positive (4–5 stars), negative (1–2 stars), or neutral (3 stars).

Q: Why is defining success important in machine learning?

A: Machine learning optimizes a training criterion, so the evaluation function must align with business goals.

Q: How can success be measured in sentiment analysis?

A: By accuracy—the percentage of correctly predicted labels.

Q: What is a classical algorithm in data mining that uses nearest neighbors?

A: The k-Nearest Neighbors (k-NN) algorithm, which classifies unlabeled objects based on the majority class of their nearest neighbors.

Q: How does k-NN work with different values of k?

A: The algorithm considers the k closest neighbors to determine the class:

• k = 3: Uses the 3 nearest neighbors

• k = 5: Uses the 5 nearest neighbors

Q: How does the k-Nearest Neighbors (k-NN) classifier learn from a training dataset?

A: It stores the training dataset and uses it to classify new instances. Its a lazy learner

Q: How are the K nearest neighbors determined in k-NN?

A: By calculating the Euclidean distance between the new instance and all training examples.