AP Physics 1 - Practice 2C

Before you start, go to Options -> Front -> Definition, then Refresh

You're all set! You may continue.

Answer C

Explanation:

Use the slope to calculate g (acceleration due to gravity):

slope = (y₂ − y₁) / (x₂ − x₁) = (7 − 0) m/s ÷ (2 − 0) s

g = slope = 3.5 m/s²

Fg = mg = (10 kg)(3.5 m/s²) = 35 N

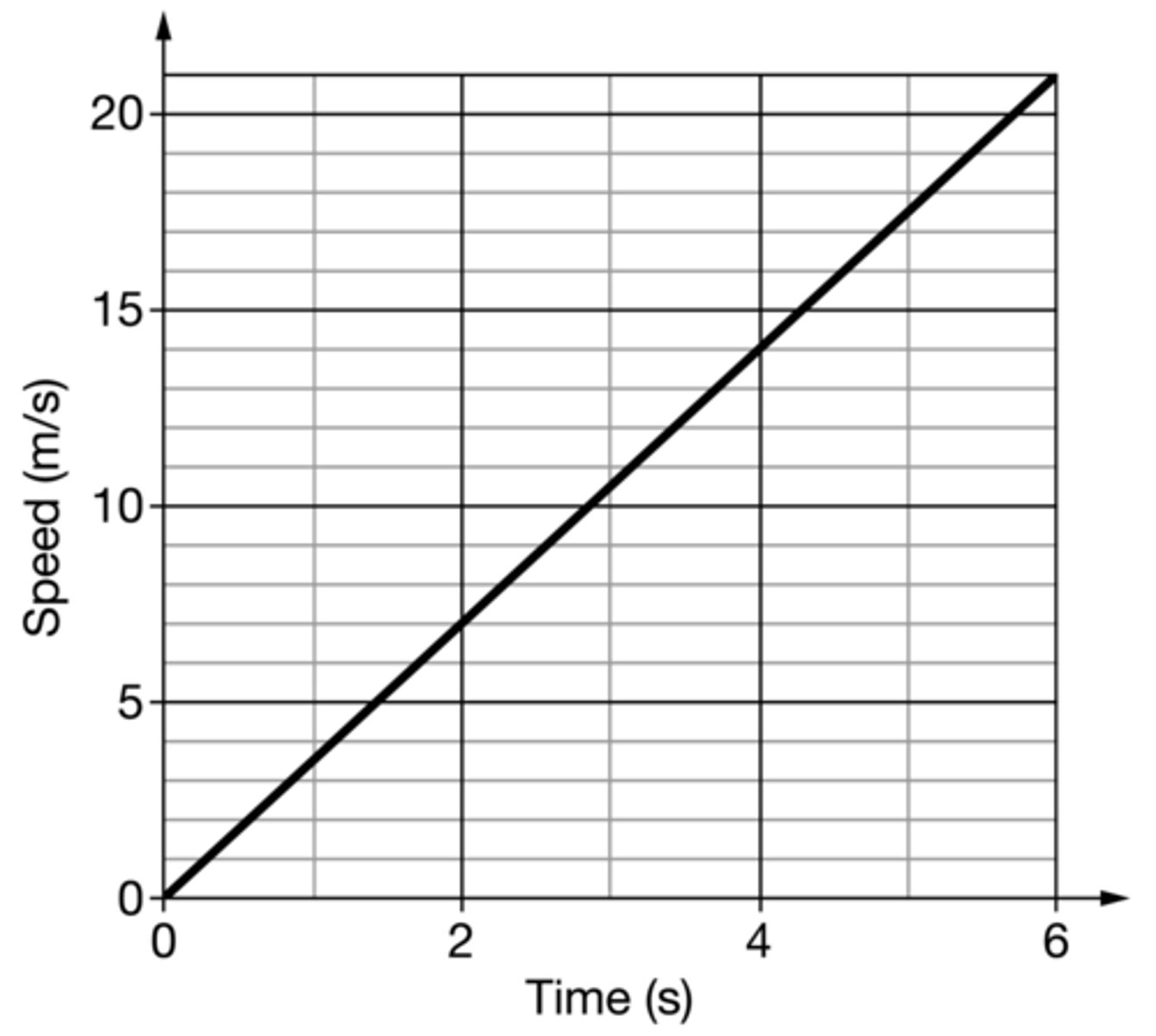
An object of mass 10 kg is released from rest above the surface of a planet such that the object's speed as a function of time is shown by the graph above. The force due to gravity exerted on the object is most nearly

A) 3.5 N

B) 7 N

C) 35 N

D) 70 N

Answer C

Explanation:

Fₙₑₜ = ma

ma = Ff

mg = 500 N -> m = (500 N) ÷ (10 m/s²) = 50 kg

a = (250 N) ÷ (50 kg) = 5 m/s²

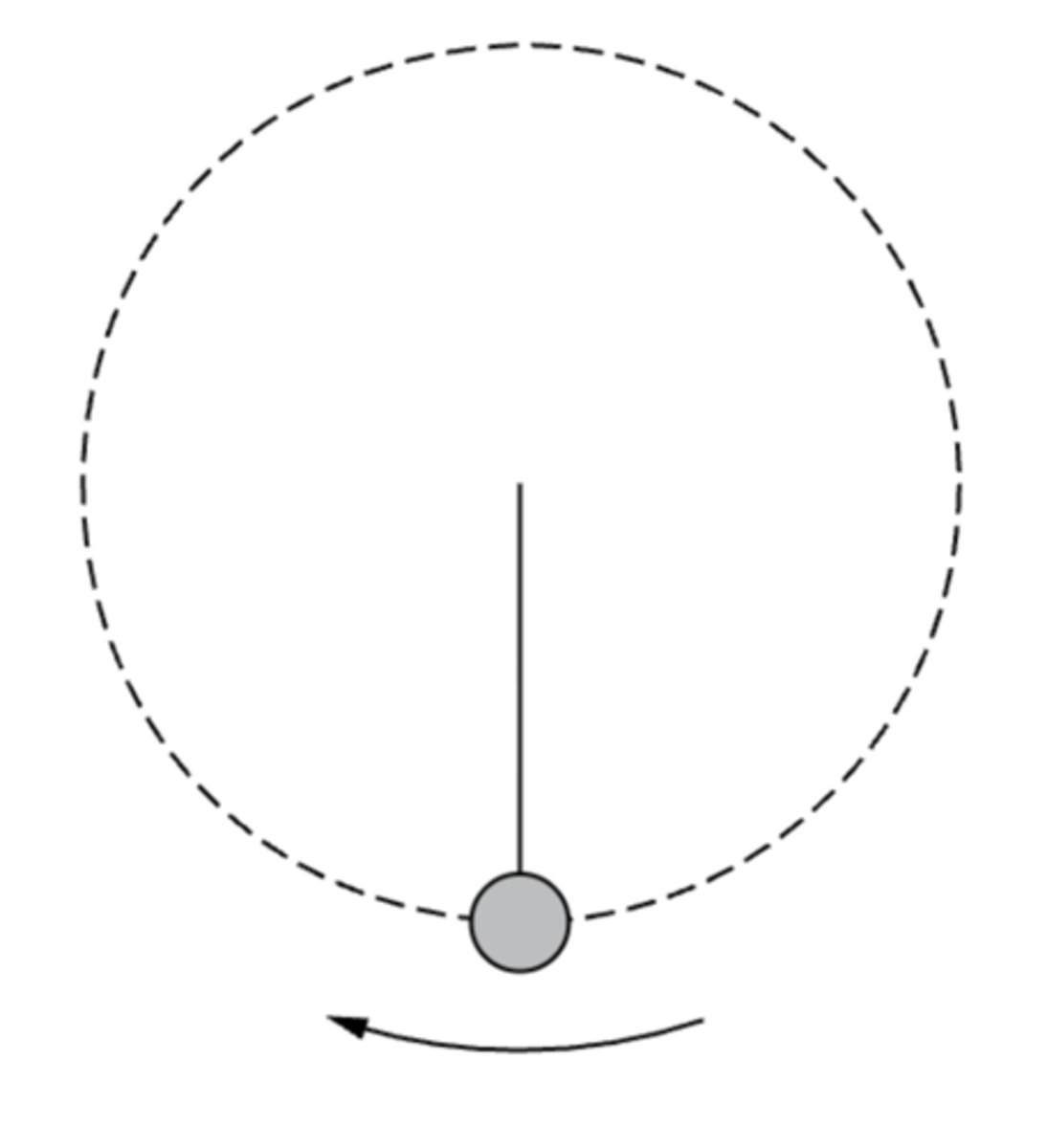
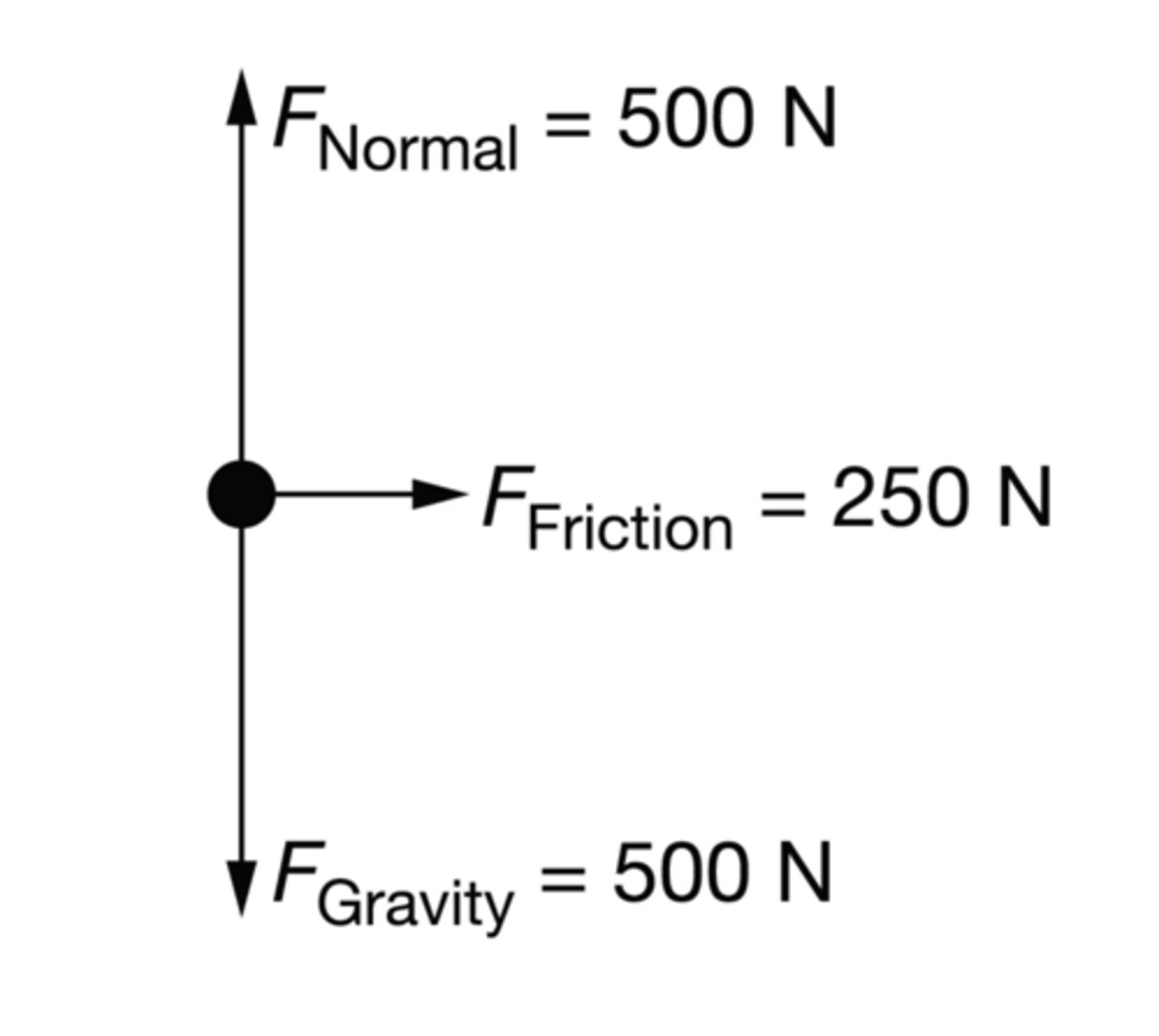
A student rides a bicycle in a circle at a constant speed and constant radius. A force diagram for the student-bicycle system is shown in the figure above. The value for each force is shown in the figure. What is the acceleration of the student-bicycle system?

A) 0 m/s²

B) 0.2 m/s²

C) 5 m/s²

D) 25 m/s²

Answer B

Explanation:

Using positive direction downward,

Fₙₑₜ = ma

ma = mg - FN

FN = m(g - a)

A person of mass m is standing on a scale in an elevator that is accelerating downward with an acceleration of magnitude a. Which of the following is a correct expression for the normal force exerted on the person by the scale?

A) mg

B) m(g - a)

C) m(g + a)

D) ma

Answer A

Explanation:

Drone and textbook have the same acceleration.

Using Newton's second law:

Fₙₑₜ = ma

Mtb a = FN - Mtb g

a = FN/Mtb - g

A delivery drone of mass Md carries a physics textbook of mass Mtb. At the instant shown, the drone has an upward acceleration. The normal force exerted on the textbook is FN. Which of the following is a correct expression for the magnitude of the acceleration of the drone?

A) FN/Mtb - g

B) FN/Md - Mtb/Md * g

C) FN/Mtb

D) Mtb/Md * g - FN/Md

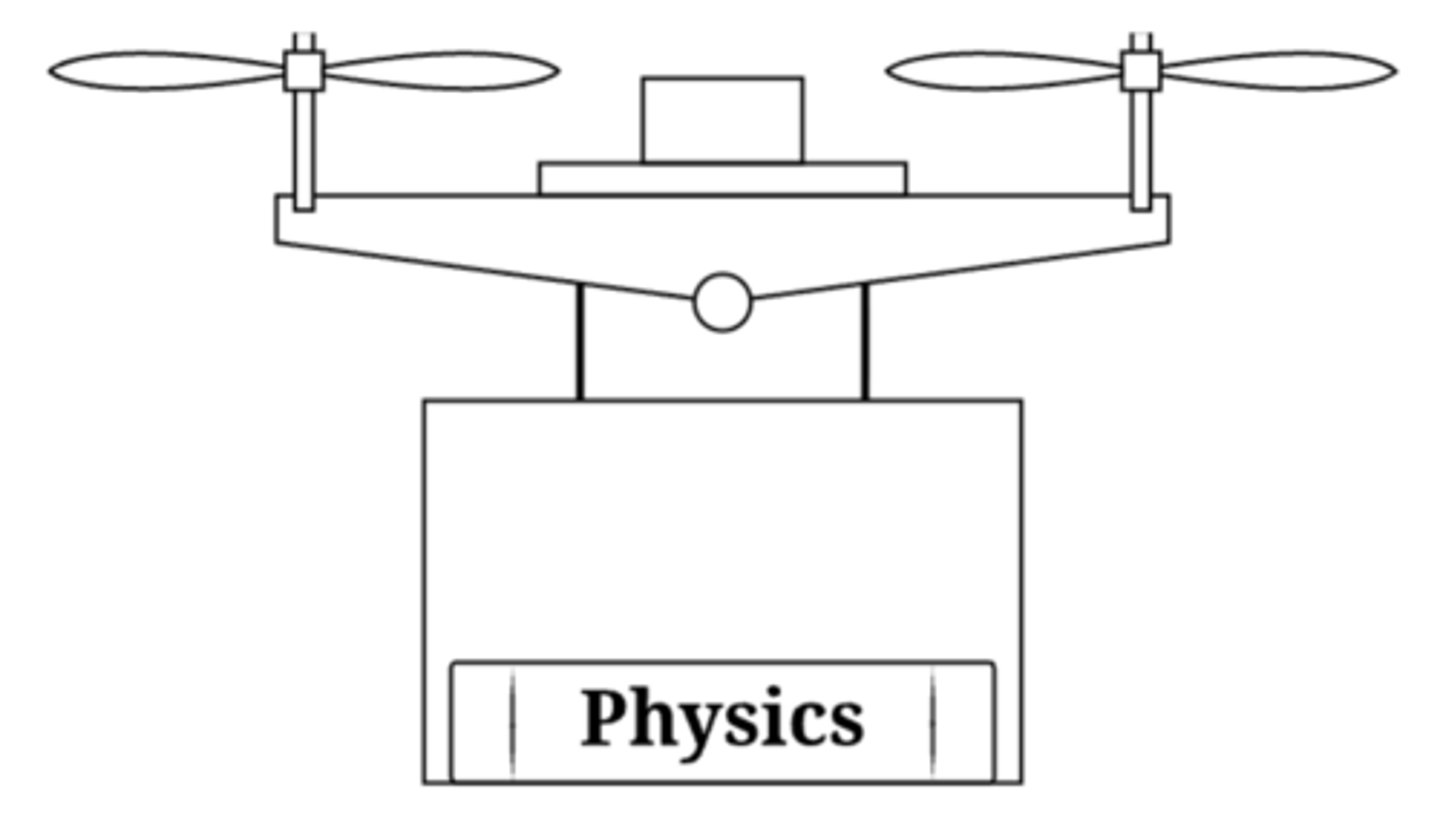
Answer D

Explanation:

Elevators traveling in constant speed, net force is zero, so apparent weight of objects are equal to their force of gravity.

Elevator A is moving upward at a constant speed of 4 m/s and Elevator B is moving downward at a constant speed of 2 m/s. In each elevator, a 10 kg object is on a scale. The scale in Elevator A reads Fa and the scale in Elevator B reads Fb. Which of the following correctly compares Fa and Fb, and provides a valid justification?

A) Fa > Fb, Elevator A moving up while Elevator B moving down.

B) Fa > Fb, Elevator A has greater speed.

C) Fa = Fb, Two objects with same mass have same apparent weight.

D) Fa = Fb, Elevators are traveling in constant speed.

Answer D

Explanation:

Force due to gravity from asteroid on astronaut pulls the astronaut back down to its surface. We can't neglect it.

An astronaut stands on the surface of an asteroid. The astronaut then jumps such that the astronaut is no longer in contact with the surface. The astronaut falls back down to the surface after a short time interval. Which of the following forces CANNOT be neglected when analyzing the motion of the astronaut?

A) Electromagnetic force

B) Strong nuclear force

C) Weak nuclear force

D) Gravitational force

Answer A

Explanation:

Force due to gravity is directly proportional to acceleration due to gravity.

A ball is moved from Earth to a planet that has a gravitational acceleration that is double that of Earth. How does the gravitational force on the ball when it is on the new planet compare to the gravitational force on the ball when it is on Earth?

A) Double

B) Half

C) Same

D) One-fourth

Answer B

Explanation:

a = v²/r -> a ~ 1/r (a is inversely proportional to radius of revolution)

a increases as r decreases

For a vs t. graph, a nonlinear increasing graph represents the centripetal acceleration.

A ball of mass M swings in a horizontal circle at the end of a string of radius R at a constant tangential speed v0. A student gradually pulls the string inward such that the radius of the circle decreases while keeping the tangential speed v0 of the ball constant, as shown above. Which of the following graphs best represents the acceleration a of the ball as a function of time t?

[ANSWER CHOICES IN DIAGRAM]

Answer B

Explanation:

Fₙₑₜ = ma

Fg = mg -> m = Fg / g = (2 N) / (10 m/s²) = 0.20 kg

Using a = v²/r and Fₙₑₜ = ma:

mv² / r = Ff

Ff = (0.20 kg)(0.60 m/s)² / (0.1 m) = 0.72 N

During an experiment, an object is placed on a disk that rotates about an axle through its center, as shown in Figure 1. The block is a distance R = 0.10 m from the center and rotates with a constant tangential speed of 0.60 m/s. A free body diagram of the forces exerted on the block is shown in Figure 2 with an unknown force of friction. What is the force of friction exerted on the block?

A) 0.50 N

B) 0.72 N

C) 5.0 N

D) 7.2 N

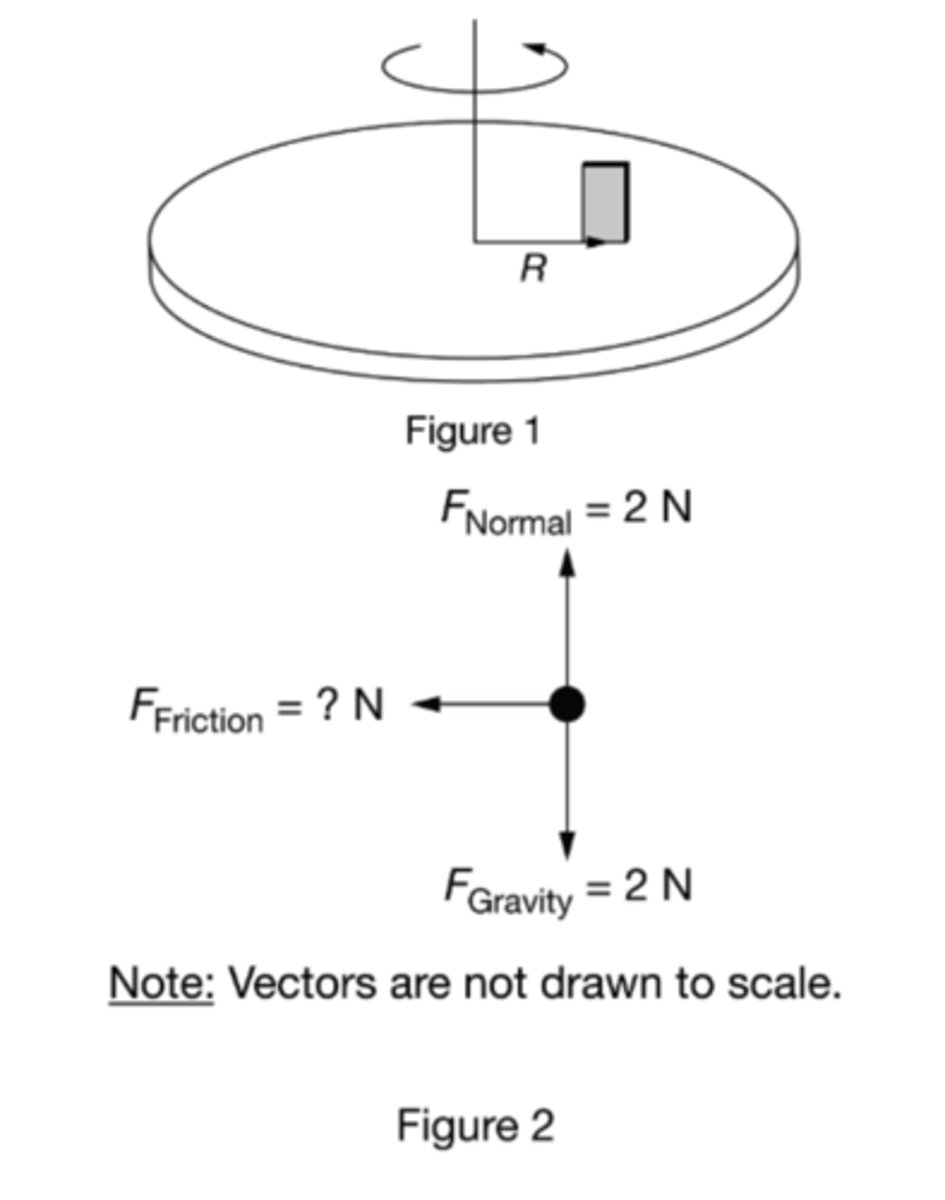
Answer B

Explanation:

Fₙₑₜ = ma

Ff = μₛmg = mv²/r -> v² = μₛgR

slope = μₛg

During an experiment, a block of mass M equals 0.20 kilograms is placed on a disk that rotates about an axle through its center, as shown in the diagram. The block is moved to different distances R from the axle, and the tangential speed of the block is gradually increased until the mass begins to slip, v max, are recorded. A student creates a graph of v max squared as a function of R, as shown. How should the student use the graph to most accurately determine the experimental value of the coefficient of static friction mu sub s between the block and the disk?

A) Determine the slope of the best fit line, and it will be equal to μs.

B) Determine the slope of the best fit line and set it equal to μs*g.

C) Determine the maximum value on the curve and use the data from that point in the equation v² = μs*gR.

D) Determine the midpoint value on the curve and use the data from that point in the equation v² = μs*gR.

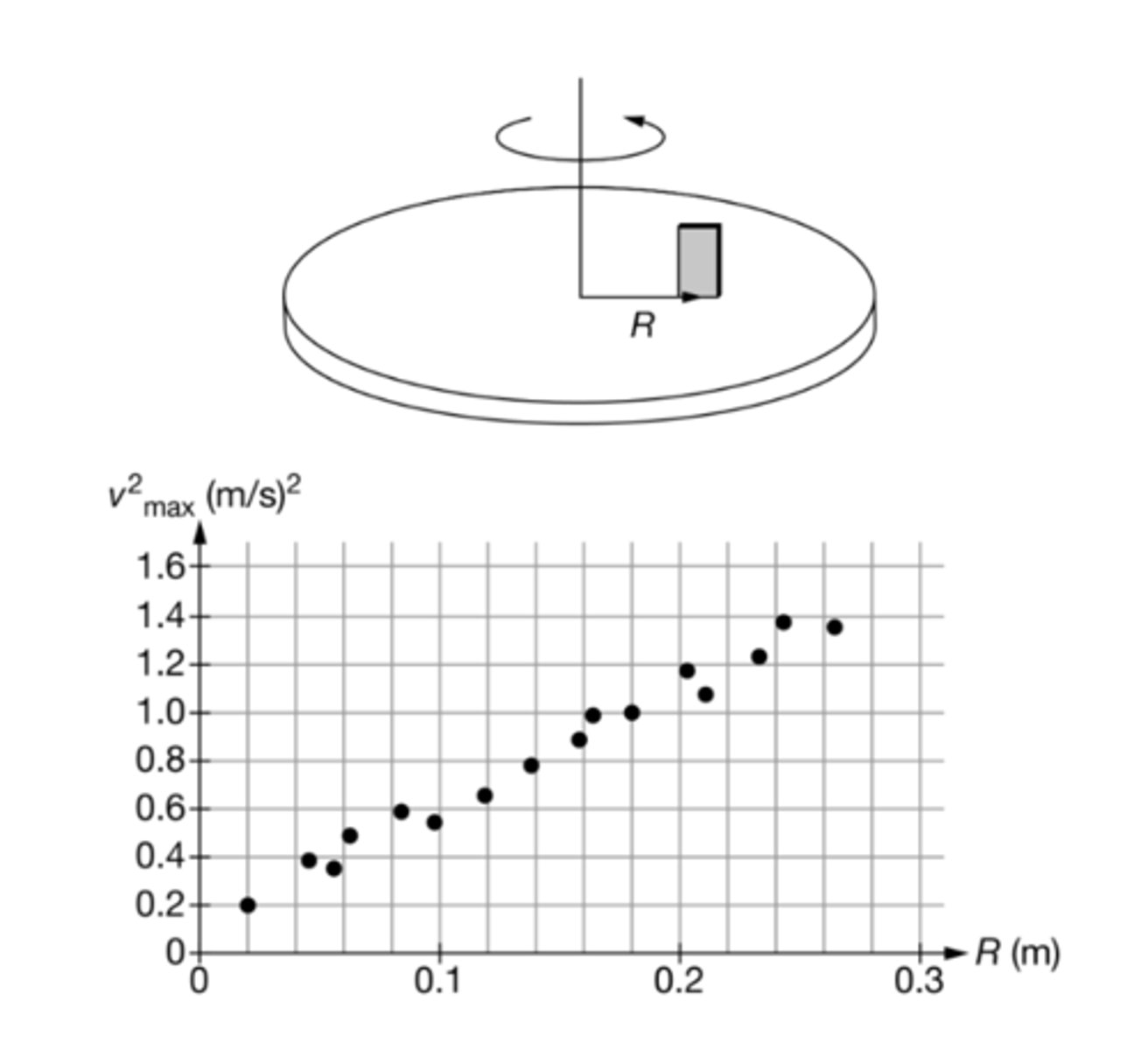
Answer C

Explanation:

Acceleration is independent of mass, so every part of the system has the same acceleration.

A block of mass M and a block of mass 3M are connected by a string, as shown above. The blocks are held with the string horizontally and are released from rest at the same time from a height H above the ground. How does the acceleration of the center of mass of the system compare to the acceleration of the object of mass M?

A) The acceleration of the center of mass is 4 times the acceleration of the object of mass M.

B) The acceleration of the center of mass is one fourth the acceleration of the object of mass M.

C) The acceleration of the center of mass is the same as the acceleration of the object of mass M.

D) The acceleration of the center of mass is initially 4 times smaller than the acceleration of the object of mass 3M, but the accelerations are the same after a long time.

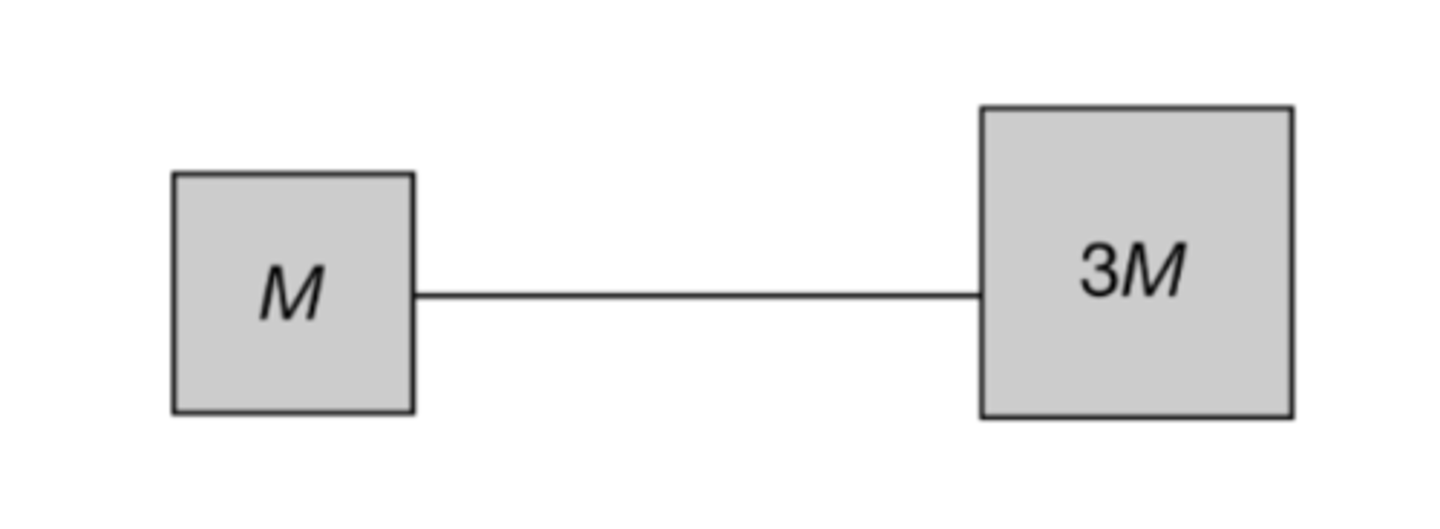
Answer C

Explanation:

Fₙₑₜ = ma

Fg = mg, -> g = Fg/m

g = (2 × 10²¹ N) / (1 × 10²⁰ kg) = 20 N/kg = 20 m/s²

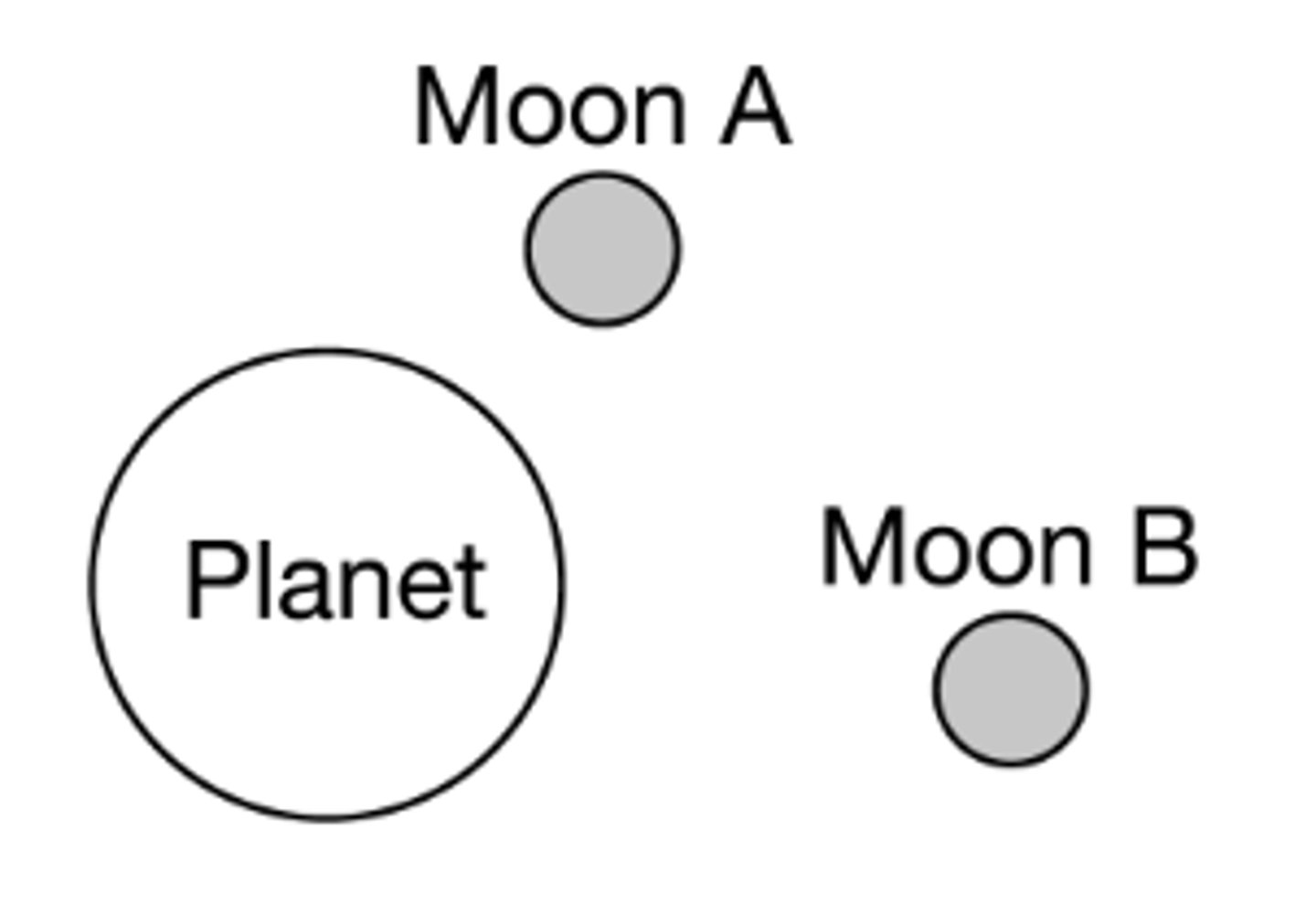
A moon of mass 1 × 10²⁰ kg is in a circular orbit around a planet. The planet exerts a gravitational force of 2 × 10²¹ N on the moon. The centripetal acceleration of the moon is most nearly

A) 0.05 m/s²

B) 10 m/s²

C) 20 m/s²

D) 2 × 10⁴¹ m/s²

Answer D

Explanation:

Fₙₑₜ = ma

mv²/r = FN - mg (Use v instead of vb for this)

FN = mv²/r + mg

FN starts at mg when vb = 0, FN ~ v².

So the graph starts at a nonzero value and is concave up.

A sled slides along a vertical circular track of radius r, as shown. There is negligible friction between the sled and the track. At the bottommost point of the track, the sled has speed vb. Which of the following graphs best show the normal force exerted by the track on the sled at the bottommost point of the track as a function of vb?

[ANSWER CHOICES IN DIAGRAM]

Answer C

Explanation:

v = 2πr / T

a꜀ = v²/r = (2πr / T)²/r = 4π²r / T²

An object of mass m travels in a horizontal circular path of radius r at constant speed. The object's period of revolution is T. What is the centripetal acceleration of the object?

A) Zero

B) g

C) 4π²r / T²

D) 2πr / T²

Answer B

Explanation:

F꜀ = mv² / r, -> F꜀ ~ v²

One end of a string is held in place and the other end of the string is attached to a disk. The disk can be set in motion and travel in a circular path with constant speed along a horizontal surface. A force sensor with negligible mass is attached to the string, as shown in the figure. There is negligible friction between both the disk and force sensor and the surface. A student sketches the graph shown of the force measured by the force sensor for several values of the speed. Is the student's sketch accurate? Why or why not?

A) Yes, because the centripetal force increases proportionally with the speed.

B) Yes, because centripetal force increases proportional to the square of the speed.

C) No, because the force should increase linearly with speed.

D) No, because the force would decrease as speed increases.

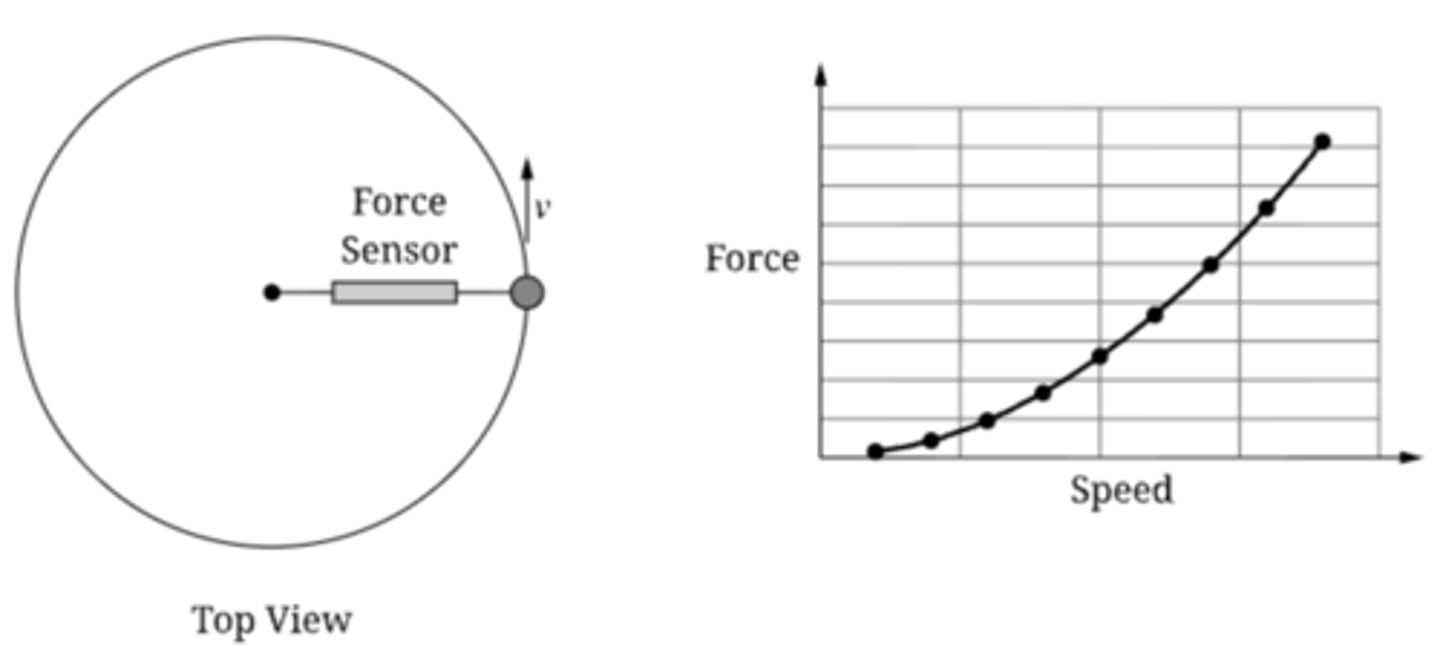
Answer D

Explanation:

Fₙₑₜ = ma

Fg = mv²/r

(GMm)/r² = mv²/r

v = √(GM/r)

When radius = R: v = √(GM/R)

When radius = 3R: vₙ = √(GM/3R)

vₙ = √(GM/R) * √(1/3)

vₙ = v * 1/√3 = v /√3

A satellite orbits Earth in a circle of radius R with speed v. The satellite is then moved into a new circular orbit with radius 3R. What tangential speed must the satellite have in order to maintain the new orbit?

A) v / 9

B) √(3v)

C) 3v

D) v /√3

Answer C

Explanation:

Cart moves in a circle, so there is centripetal force is directed toward the center of the circle. Tangential speed of cart is increasing, so there must also be a force in the direction of cart's motion. Net force is the vector sum of these two forces, which will be directed between the radial and tangential directions.

A cart is moving along a horizontal circular track. At the instant shown, the cart is moving to the right and its speed is increasing. A student claims that the net force on the cart is directed toward the center of the track. Is the claim correct? Why or why not?

A) Yes, centripetal force always points toward the center of the circular motion.

B) Yes, speed of the cart is increasing so there must be a nonzero net force.

C) No, cart has tangential acceleration parallel and centripetal acceleration perpendicular to the track.

D) No, speed is increasing, so net force is directed to the right.

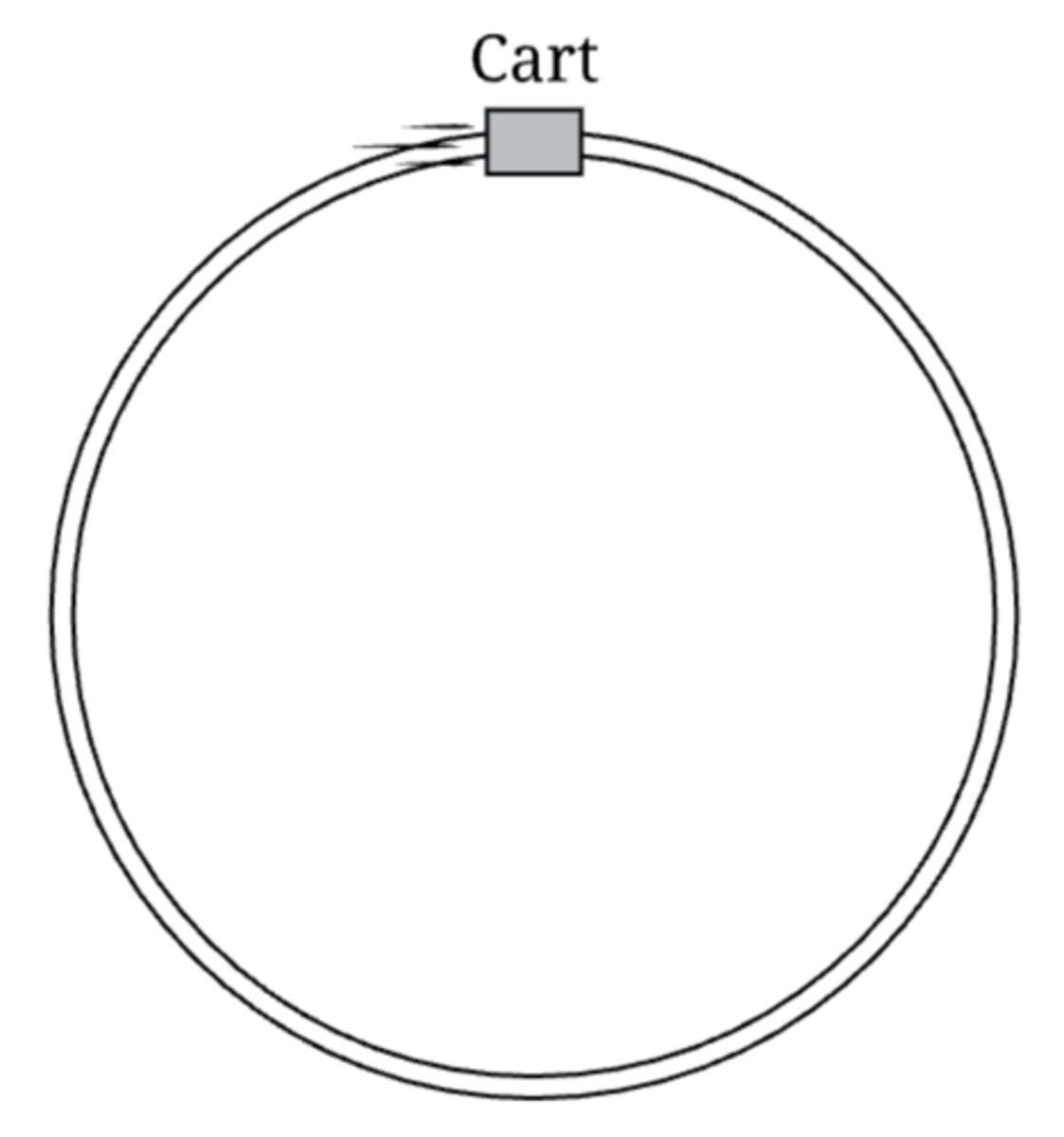
Answer A

Explanation:

The net force responsible for the penny's circular motion is the force of static friction. Applying Newton's second law and the acceleration of an object in circular motion yields:

ma꜀ = Ff,ₛ

mv² / r = μₛFN

Since the penny is on a horizontal surface that does not accelerate vertically, the normal force equals the gravitational force on the penny.

mv² / r = μₛmg

μₛ = v² / rg

A penny of mass m is revolving at the edge of a spinning turntable of radius r, as shown. The penny has a constant tangential speed v, which is the maximum speed the penny can have without slipping. Which of the following is a correct expression for the coefficient of static friction, mus, between the penny and the turntable?

A) v² / rg

B) v² / mrg

C) mv² / rg

D) v² / r

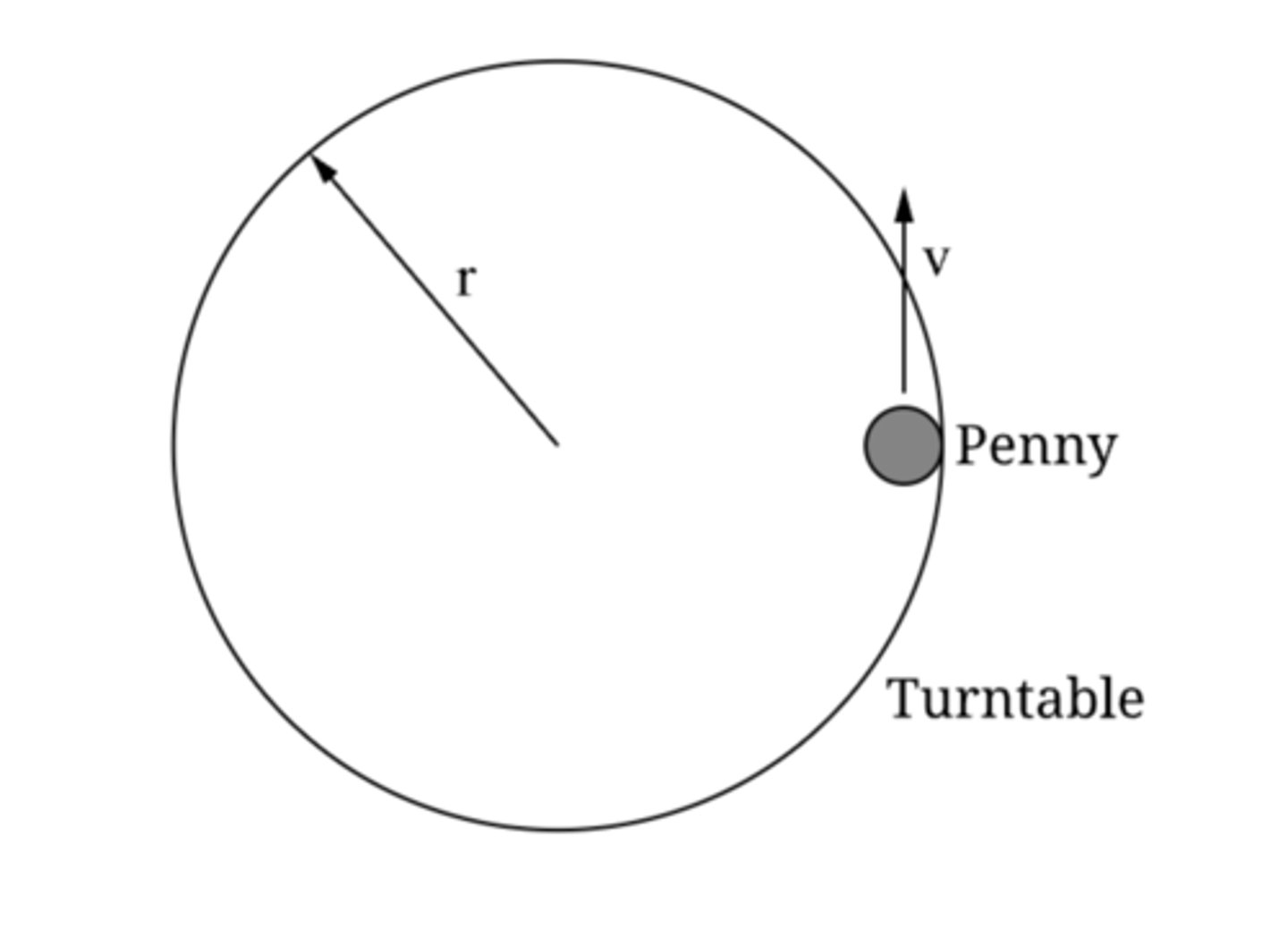
Answer D

Explanation:

T = 2πr / v

Fₙₑₜ = ma

mv² / r = Fg

GMₑmₛ / r² = mₛv² / r

v = √( GMₑ / r ) = √( GMₑ / (Rₑ + h) )

Substituting this expression of v into the expression for T yields:

T = 2π (Rₑ + h) / √( GMₑ / (Rₑ + h) )

T = 2π √( (R_E + h)³ / (G M_E) )

A satellite of mass mₛ is in a circular orbit at a height h above the surface of Earth, which has a mass Mₑ and a radius Rₑ. What is the period of the satellite's orbit?

A) 2π√( Rₑ³ / Gmₛ )

B) 2π√( Rₑ³ / GMₑ )

C) 2π√( (Rₑ + h)³ / Gmₛ )

D) 2π√( (Rₑ + h)³ / GMₑ )

Answer D

Explanation:

T = 2πr / v

Tₐ = 2/3 Tʙ

T𝖼 = 1/4 Tʙ

=> Tₐ = 8/3 T𝖼

Three wheels are arranged as shown in the diagram. Wheel B has radius R and period Tʙ. Wheel A has radius 2R/3, and Wheel C has a radius R/4. The wheels turn each other without slipping. Which of the following correctly relates the period Tₐ of Wheel A to the period T𝖼 of Wheel C?

(A) Tₐ = 3/8 T𝖼

(B) Tₐ = 2/3 T𝖼

(C) Tₐ = T𝖼

(D) Tₐ = 8/3 T𝖼

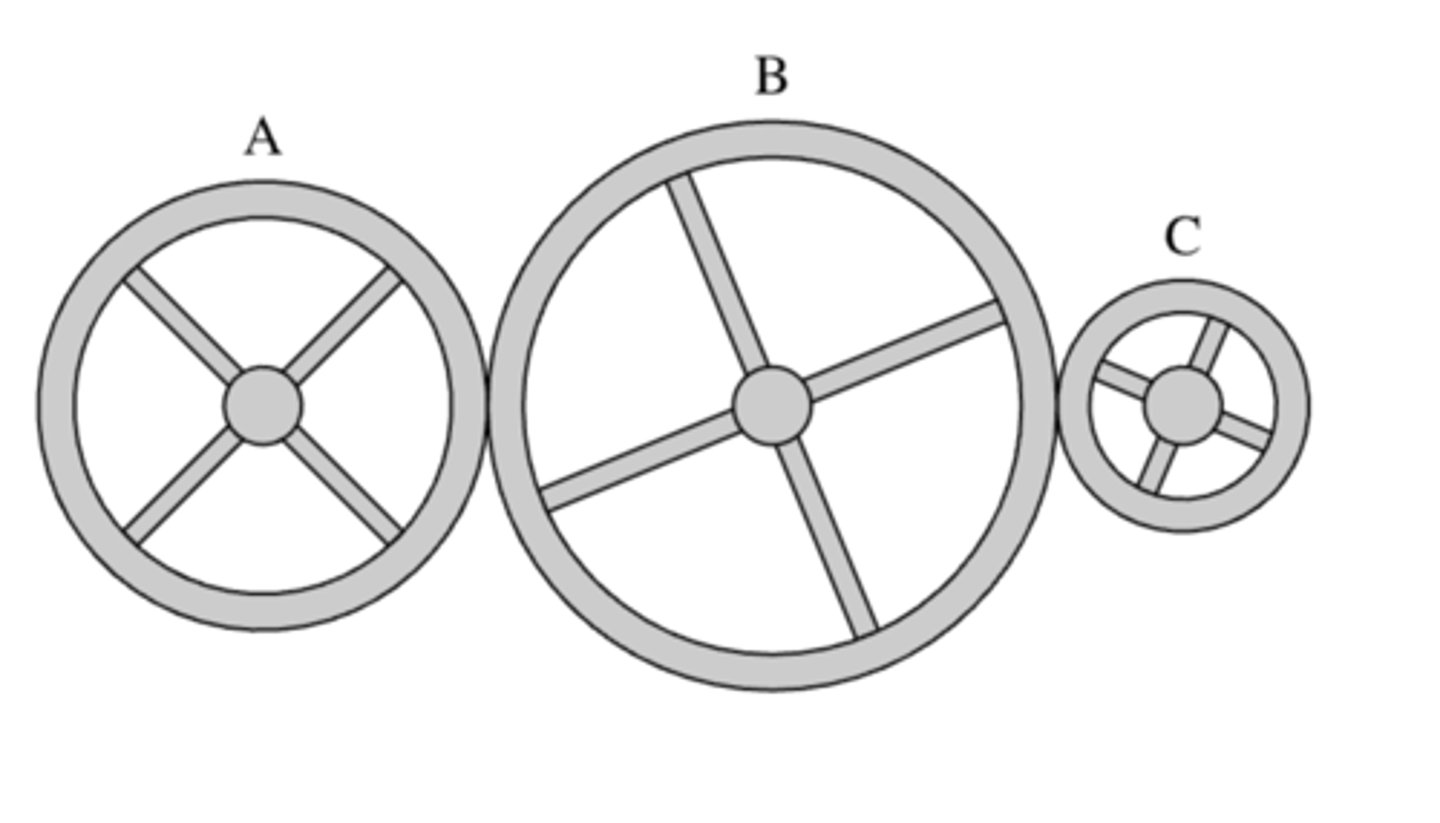
Answer A

Explanation:

Tension has constant magnitude. At topmost point, tension and force of gravity have same direction, so net force is maximum. Net force is proportional to the speed squared, so ball will have the largest speed where the net force is greatest.

A motor swings a ball on a string in a vertical circle such that the tension in the string is constant throughout the ball’s motion. Which of the following correctly indicates at which point the ball has the greatest speed and provides a valid justification?

(A) Topmost point, tension force and gravitational force are both directed toward center.

(B) Topmost point, net force is zero.

(C) Bottommost point, tension offsets gravitational force.

(D) Bottommost point, net force is maximum.