precalc honors chp 10 analytic geometry exam

general equation of a conic:

Ax² + Cy² + Dx + Ey + F = 0

how do you complete the square?

step 1. move all constants and any variables that are not squared (this is for parabolas) to one side

step 2. complete the square. take “b” divide by 2, square that number, and make it c. if there is something outside that has been factored, you need to multiply by that when you put it on the other side

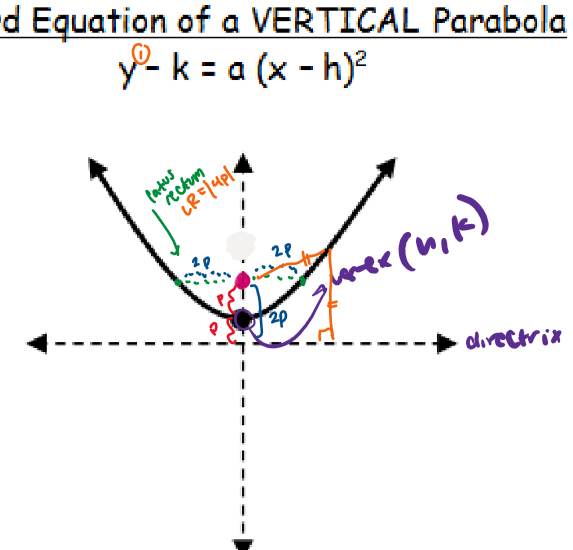
what does a vertical parabola look like

pay attention to the fact that your point that you draw everything on is called your VERTEX (for every other shape it would be the center!)

hard vs. soft brackets

remember that u need hard brackets [ for any point that it actually touches

what is the significance of “p” in parabola graphs

a = 1/4p

p is what determines the points for pretty much everything

p is ALWAYS POSITIVE because it just expresses a distance

the length of the latus rectum, or LR is |4p|

if a is positive, the parabola opens up or right

if a is negative, the parabola op

need to knows for circle

there should not be a denominator in your final equation

r² is part of the final equation, make sure you know that you have to take the square root of that value to find r itself

circles only need radius and center pretty much

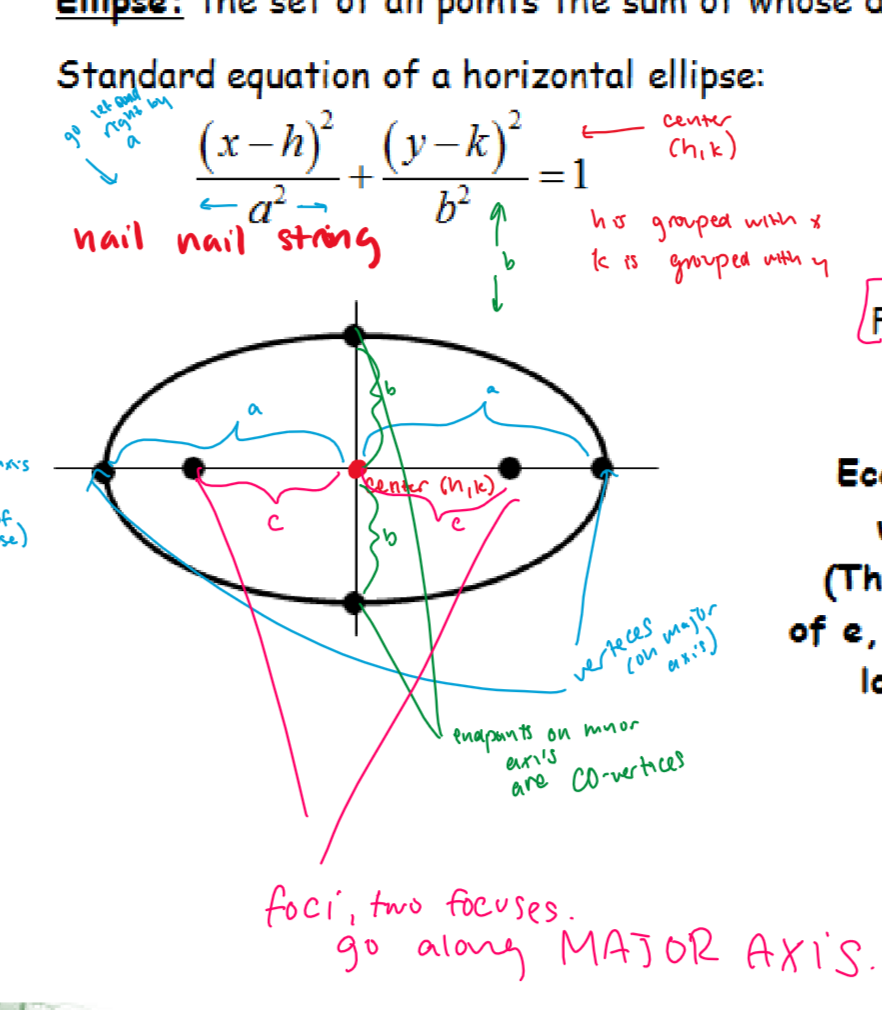
what does a horizontal ellipse look like

a=larger value

b=smaller value

^remember that in the final equation these values are squared and you need to take the squared root of them to find a and b themselves

vertices on major axis, COVERTICES on minor axis

your foci, or “c” goes on the same axis as the a value. this axis (the longer one) is called the MAJOR AXIS (2a)

the minor axis is your axis that is smaller (2b)

how do you know the difference between hyperbolas and ellipses

hyperbola—minus sign between both terms, foci is outside of vertices

ellipse—plus sign, foci is inside of vertices

both will always equal 1 on the right side

eccentricity on ellipse

e = c/a, where 0 < e < 1 (the smaller the value of e, the more the ellipse looks like a circle)

vertical ellipse

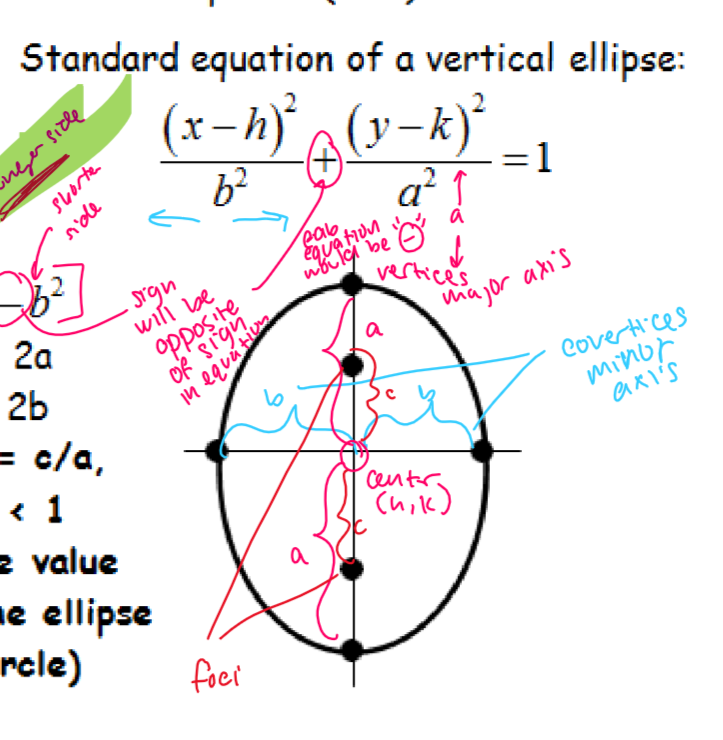
how do you find foci on an ellipse?

CAB EQUATION c² = a² - b²

what you will be needing to mark for each eq.

parabola: directrix, LR, vertex, focus (marked with an F)

circle: center, radius

ellipse: length of major axis, length of minor axis, center, vertices, CV, foci (marked with c), possibly a, b, and c

hyperbola: foci, center, eq. of asymptote, a, b, and c, sketch box and asymptotes, transverse vs. conjugate axis

horizontal hyperbola

“a” is whichever number has a positive sign in front of it, NOT which number is bigger

a is also the same axis that the foci will be on (transverse axis). foci are outside of the eq.

form box by connecting vertices and covertices together

indicate center (h, k)

foci: c² = a² + b²

transverse axis = 2a

conjugate axis = 2b

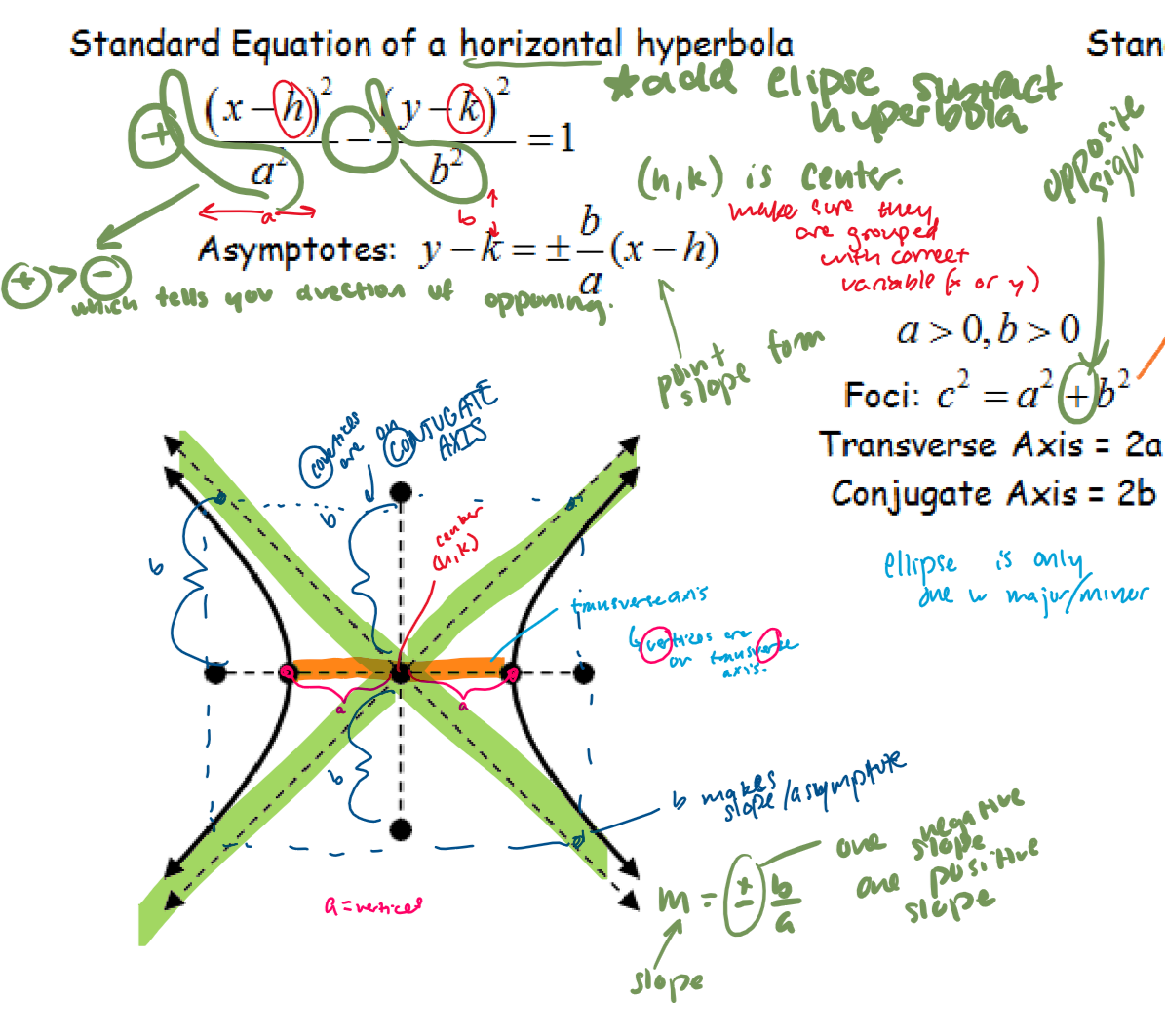
hyperbola asymptote formula—horizontal asymptotes

y - k = +- b/a(x-h)

hyperbola asymptote formula—vertical asymptotes

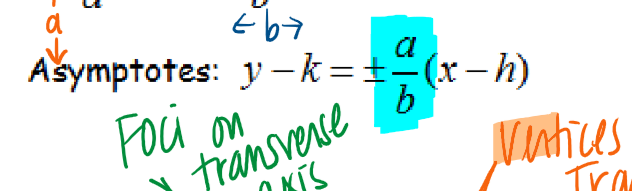
vertical hyperbola

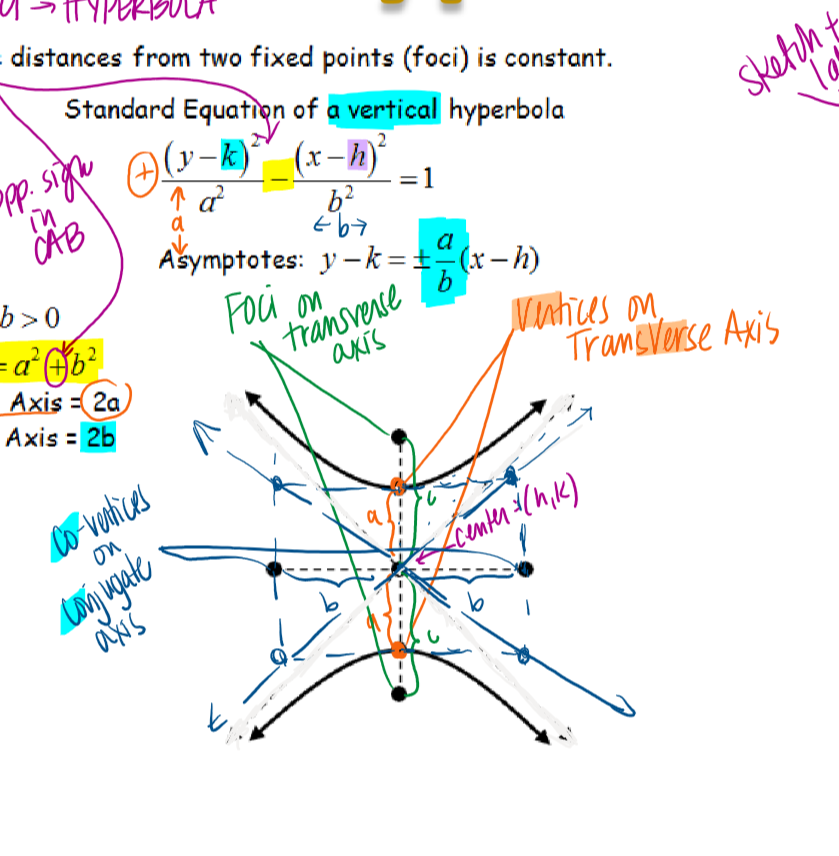
hyperbola asymptotes

dashed lines

REMINDER THAT:

a is different from a². make sure u have a² in your standard equations and NOT a

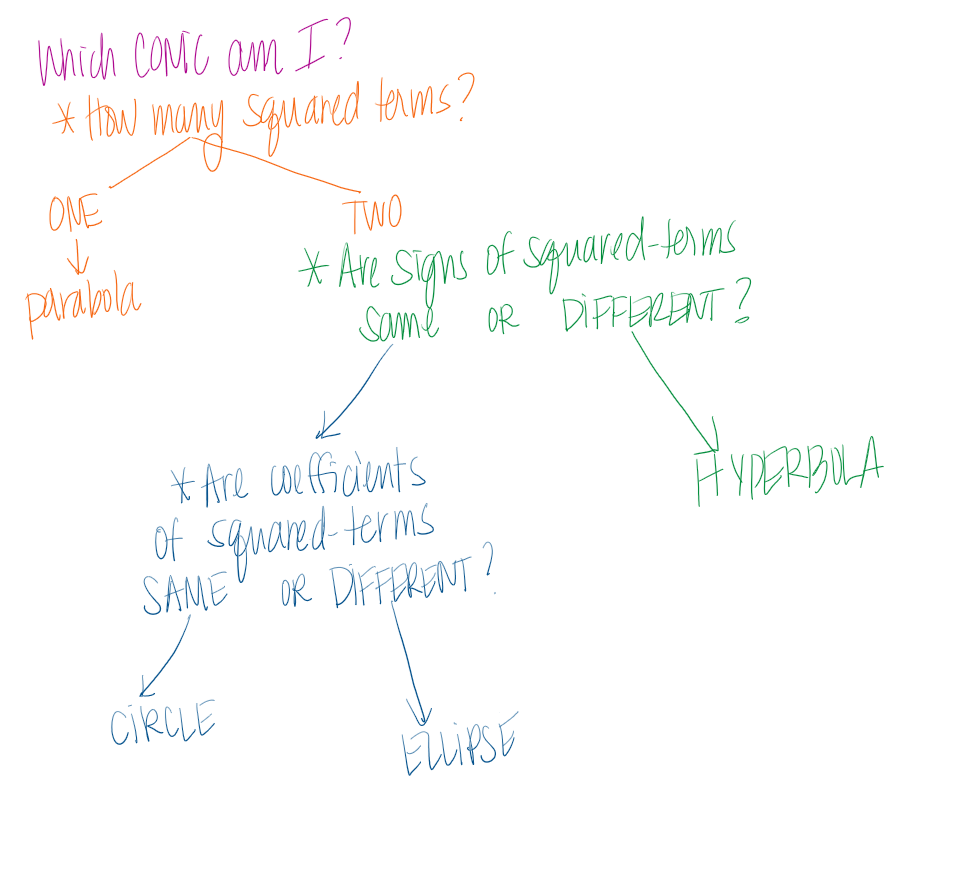
which conic am i?

yeahhhh