Hfdst2. Discrete Wiskunde 1BA Theorie
4.7(3)Studied by 11 people
Card Sorting
1/30
Earn XP
Description and Tags
Last updated 2:29 PM on 12/28/22
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
31 Terms
1
New cards
Definitie: partiële orderelatie
Een relatie die reflexief, anti-symmetrisch en transitief is.
2
New cards
Definitie: totale orderelatie
Een orderelatie R ⊂ A² is totaal als voor elke twee verschillende elementen ‘x’ en ‘y’ uit A, het koppel (x,y) of (y,x) tot R behoort.
3
New cards
Definitie: benedengrens
Een benedengrens b ∈ A van verzameling X ⊂ A, is een getal dat kleiner of gelijk is aan alle elementen van X.
4
New cards
Definitie: kleinste element
Het kleinste element van een verzameling is een benedengrens die tot die verzameling behoort.
5
New cards
Axioma van de goede ordening/het well-ordeningsaxioma
Een niet-ledige deelverzameling van een verzameling met een ondergrens, bezit een kleinste element.
6
New cards
Formuleer en Bewijs: principe van het kleinste tegenvoorbeeld.
p19

7
New cards
Formuleer en bewijs: inductieprincipe
p19

8
New cards
Leg uit in eigen woorden: laden/duivenhokprincipe
Veronderstel dat we m objecten willen verdelen over m-1 laden, dan is het onmiddellijk duidelijk dat, indien er meer objecten zijn dan laden, er ten minste 1 lade zal zijn die meer dan 1 object bevat.
9
New cards
Aftelbare verzameling
Een oneindige relatie X is aftelbaar als er een bijectie bestaat van **N** naar X.
10
New cards
Bewijs: De verzameling van de gehele getallen is aftelbaar
p23

11
New cards
Bewijs: De verzameling van de rationale getallen is aftelbaar
p24

12
New cards
Bewijs: De verzameling van de reële getallen is niet aftelbaar
p24-25

13
New cards
Definitie: Variatie
Een variatie van k elementen uit n elementen is een geordend k-tal van k verschillende elementen gekozen uit een gegeven verzameling van n elementen. (n >= k en k, n ∈ **N**)
14
New cards
Bewijs: P(n,k) = n(n-1)…(n-(k-1))
p30

15
New cards
Definitie: Permutatie
Een variatie van ‘n’ elementen uit ‘n’ elementen.
16
New cards
Definitie: Combinatie
Een combinatie van k elementen uit n elementen is een deelverzameling met k elementen uit een gegeven verzameling van n elementen. (n >= k en k, n ∈ **N**)
17
New cards
Bewijs: P(n,k) = C(n,k) \* k!
p32

18
New cards
Eigenschap: C(n,k) = …
p33
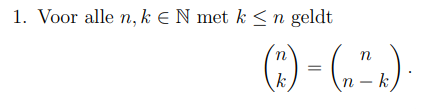
19
New cards
Eigenschap + bewijs: C(n, k+1) = …
p33
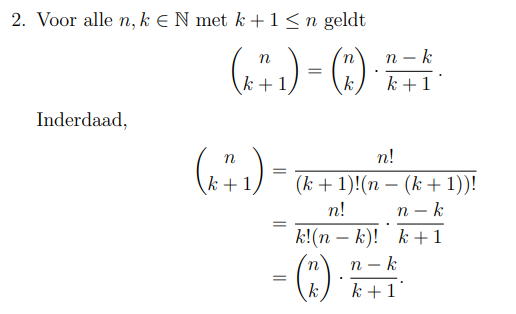
20
New cards
Eigenschap + bewijs: formule van Stifel-Pascal
p33

21
New cards
Definitie: Herhalingsvariatie
Een herhalingsvariatie van k elementen uit n elementen is een geordend k-tal elementen uit een verzameling van n elementen. (n >= k en k, n ∈ **N**)
22
New cards
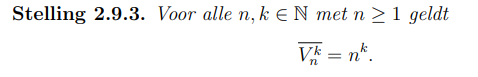
Bewijs:
p34
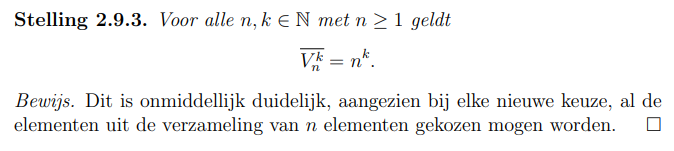
23
New cards
Definitie: Herhalingscombinatie
Een herhalingscombinatie van k elementen uit n elementen is een niet-geordend k-tal elementen, gekozen uit een verzameling van n elementen. (n >= k en k, n ∈ **N**)
24
New cards
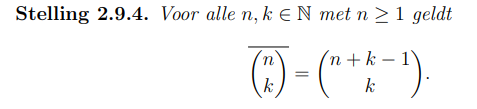
Bewijs:
p35

25
New cards
Formuleer en bewijs: binomiaalstelling

26
New cards
Formuleer en bewijs: veralgemeend inclusie-exclusie principe / zeefprincipe

27
New cards
Definitie: Wanorde
Een permutatie zonder fixelementen (bijectie waarbij geen enkel element beeld is van zichzelf)
28
New cards
Formule wanorde: niet recursief
p40
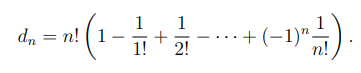
29
New cards
Formule wanorde: recursief met beginvoorwaarden
d1 = 0, d2 = 1
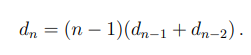
30
New cards
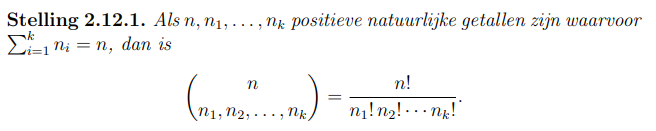
Bewijs:
p45

31
New cards
Formuleer en bewijs: multinomiaalstelling
p46
