Cours 4 - Fréquences, mesures de tendance/centrale/dispersion/position, normale centrée réduite

Présentation des fréquences

Qu’est-ce qu’une fréquence ?

Nombre d'observations associées à une valeur ou catégorie.→ c-à-d, à quelle fréquence cette valeur ou catégorie est-elle observée dans une population

Qu’est-ce qu’une fréquence cumulée ?

Nombre d’observations associées à une valeur + toutes les valeurs précédentes.

Types de mesure de la fréquence

Qu’est-ce qu’une proportion ?

Fréquence ÷ nombre total d’observations

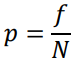
Quelle est le type de mesure de la fréquence de la proportion?

mesure relative :

• Contrairement à une valeur absolue (ex. « 200 personnes »), une proportion compare un sous-ensemble à l’ensemble total.

• Elle met donc en relation :

  • Numérateur = la partie de la population qui présente la caractéristique étudiée.

  • Dénominateur = la population totale sur laquelle on fait la mesure.

Pourquoi utilise-t-on les proportions ?

Pour comparer des distributions de populations de tailles différentes.

Qu’est-ce qu’un pourcentage ?

Une proportion rapportée à 100 observations.

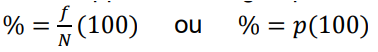
Comment calculer la fréquence à partir d’une proportion ou d’un pourcentage?

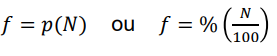
Qu’est-ce qu’un rapport (ratio) ?

Relation entre deux quantités qu’on veut comparer (ex. 6 hommes / 7 femmes).

Qu’est-ce qu’un taux ?

Rapport dynamique qui mesure un changement dans le temps (souvent le nb de personne par unité de temps c.-à-d. qu’on attribue à chaque personne un poids selon la durée de son observation).

Tableau avec chaque type de mesure de  fréquences

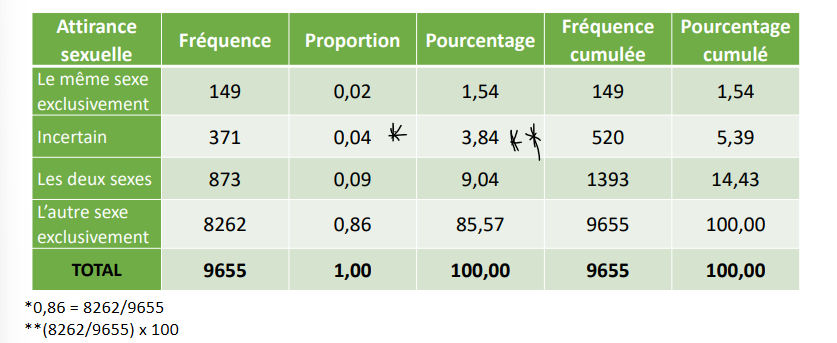
Représentations graphiques

Quels sont les 5 représentations graphiques de fréquences

1. histogramme de fréquences

2. polygone de fréquence

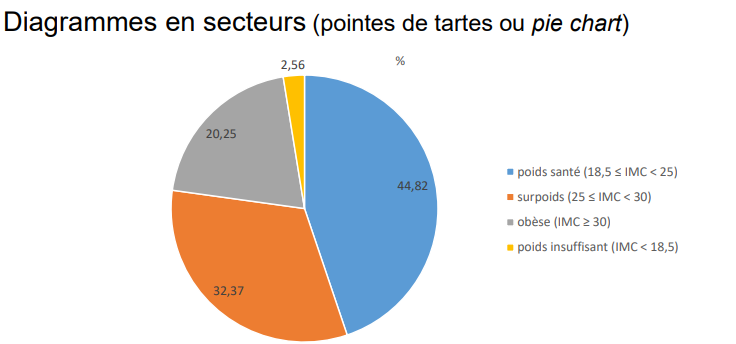
3. diagrammes en secteurs (pie chart)

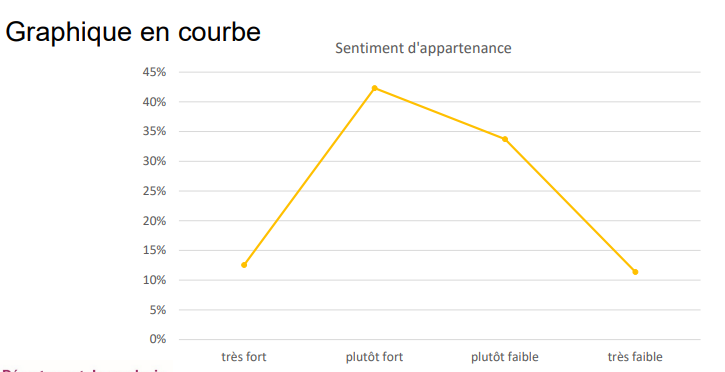
4. graphique en courbe

5. boîte à moustache

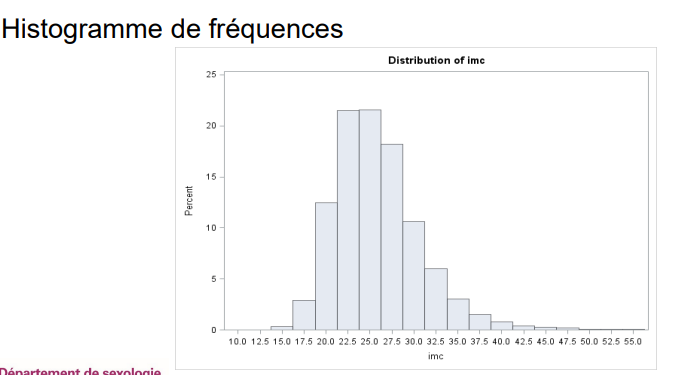
Qu’est-ce qu’un histogramme de fréquences ?

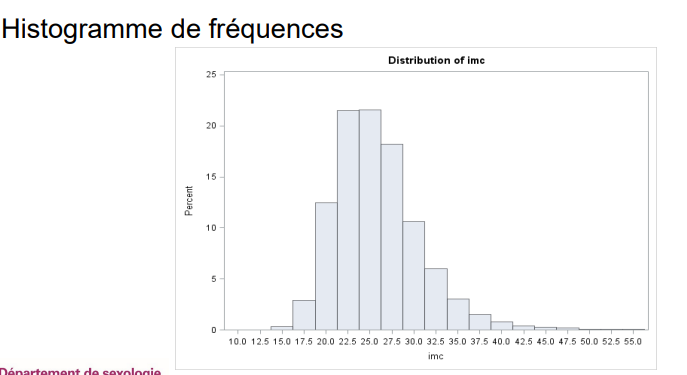
À quoi sert un histogramme de fréquence ?

À montrer le nombre précis de personnes dans chaque catégorie.

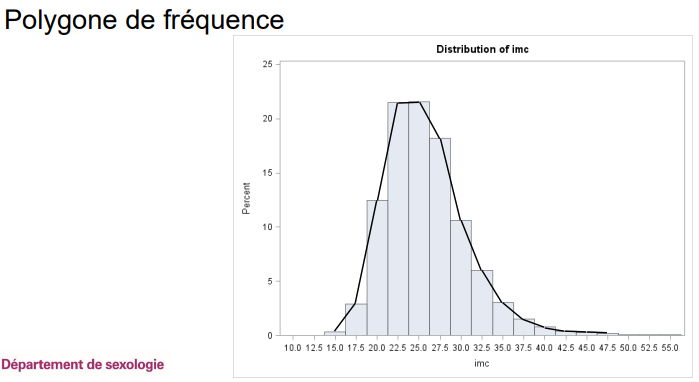
Qu’est-ce qu’un polygone de fréquence ?

Qu’est-ce qu’un diagrammes en secteurs?

Qu’est-ce qu’un graphique en courbe ?

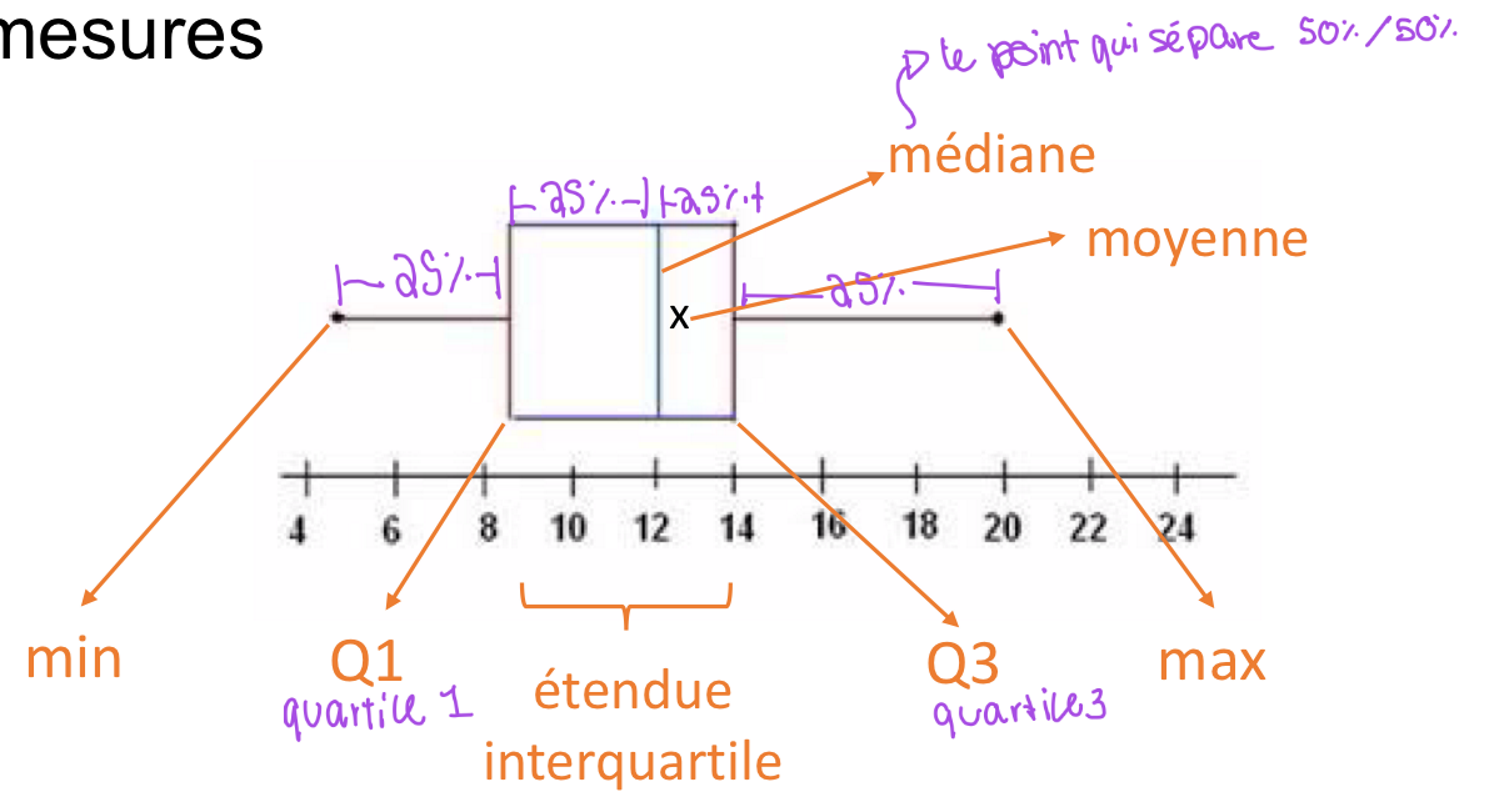
Qu’est-ce qu’une boîte à moustache (définition et représentation)?

Représentation graphique d'une distribution qui intègre différentes mesures  → facilite la comparaison des populations

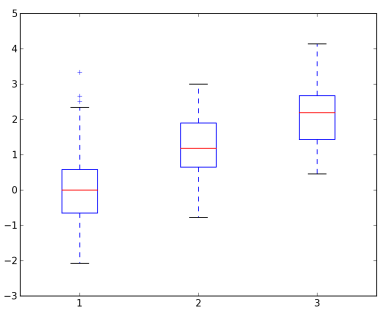
À quoi sert une boîte à moustache ?

À comparer des populations lorsqu’on fait plusieurs boîtes à moustache sur un graphique.

Mesures de tendance centrale

Qu’est-ce qu’une tendance centrale ?

Ce qui est typique d’une population, la valeur autour de laquelle les données se regroupent.

Qu’est-ce qui est distribué à l’aide d’une tendance centrale?

 propriété d’une population (Ø d’un individu)

Quelles sont les 4 mesures de tendance centrale ?

Moyenne, moyenne pondérée, médiane, mode.

Qu’est-ce que la moyenne ?

Somme des observations ÷ nombre d'observations.→ mesure de tendance centrale la plus connue

Qu’est-ce que la moyenne pondérée ?

Moyenne qui tient compte d’un poids différent pour chaque observation.

La moyenne pondérée est plus souvent utilisée pour distribuer quoi?

une moyenne finale d’examens tous pondérés

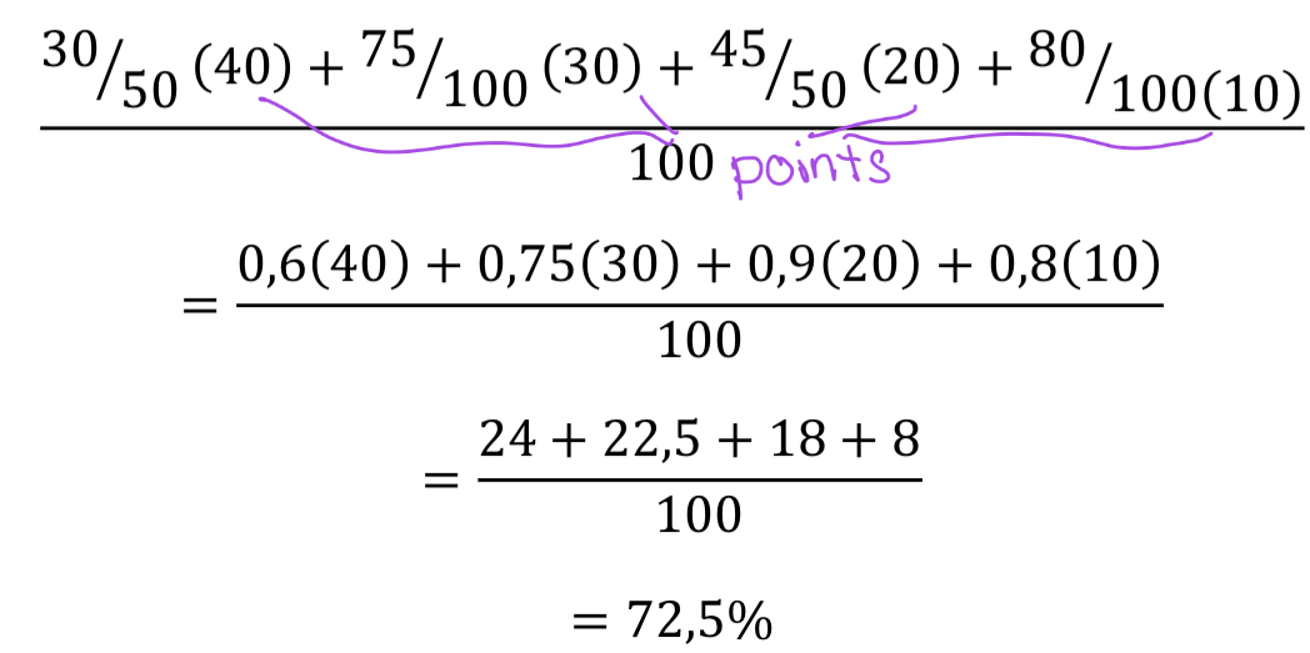
Qu’est-ce que la médiane ?

Valeur au centre de la distribution (50% de chaque côté).

Quand utiliser la médiane ?

Quand il y a des valeurs extrêmes.

Qu’est-ce que le mode ?

La valeur ou catégorie la plus fréquente.

Quand utiliser le mode ?

Pour des variables nominales ou ordinales (donc qualitatives) car ces variables ne peuvent être calculée

Mesures de dispersion

Pourquoi utiliser des mesures de dispersion ?

Pour décrire la variabilité autour de la tendance centrale expliqué par l’hétérogèinité des populations

Quelles sont les 5 mesures de dispersion ?

Étendue, écart moyen, variance, écart-type, coefficient de variation.

Qu’est-ce que l’étendue ?

Différence entre la valeur max et la valeur min.

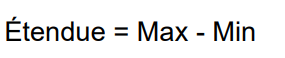
Qu’est-ce que l’écart moyen ?

Distance moyenne entre chaque valeur et la moyenne.« une valeur est à combien de la moyenne »

Qu’est-ce que la valeur absolue?

fonction qui transforme tout nombre négatif en positif (et laisse les positifs inchangés).

Qu’est-ce que la variance ?

même calcul que l'écart moyen, mais au lieu d'utiliser une valeur absolue (pas idéale pour des raisons mathématiques), on utilise les écarts au carré pour éviter que la valeur soit négative

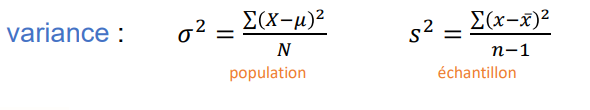
Qu’est-ce que l’écart-type ?

Racine carrée de la variance pour qu’elle soit plus facile à interpréter → mesure la dispersion la plus utilisée.

Qu’est-ce que le coefficient de variation (CV) ?

Variabilité exprimée relativement à la moyenne (plus petit = plus homogène).

Comment le coeeficient de variation montre-t-il si les valeurs sont distribuées proche ou loin de la moyenne?

plus le CV est petit, plus les valeurs de la distribution tendent à être proches de la moyenne

Forme de la distribution

Comment représente-t-on les distributions visuellement?

on les compare à la distribution de la courbe normale; une distribution est qualifiée de bonne ou mauvaise en fonction de son écart par rapport à la courbe normale

Quels sont les 2 types de distribution qui démontre clairement une différence à la courbe normale  ?

Asymétrie et aplatissement.

Qu’est-ce que l’asymétrie ?

Décalage de la distribution vers la gauche ou la droite.

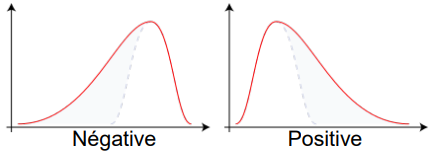
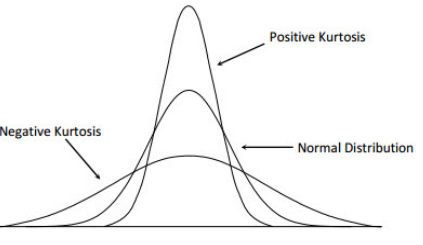
Qu’est-ce que l’aplatissement ?

Concentration forte ou faible des valeurs autour de la moyenne.

Quelle mesure de tendance centrale à utiliser selon la situation?

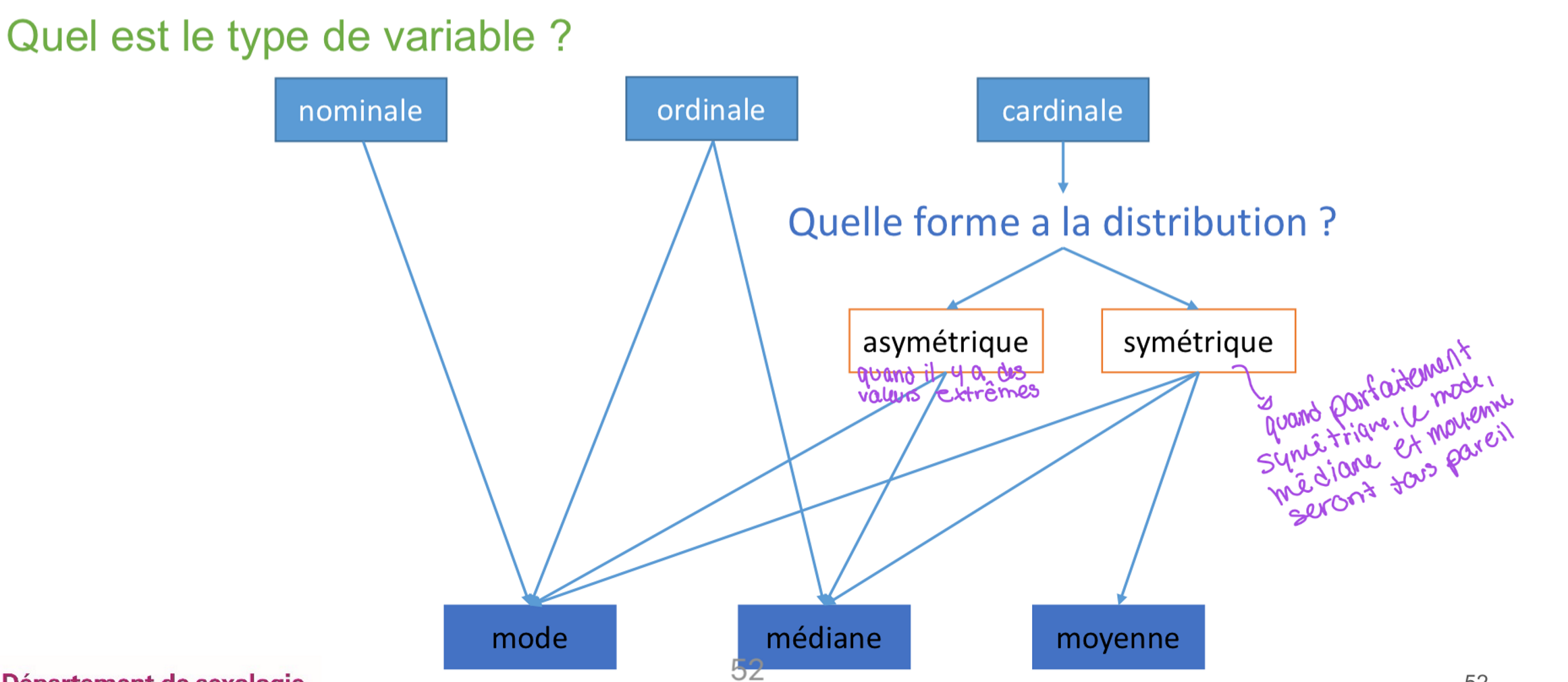
Quelles sont les particularités de mode, médiane et moyenne en détails pour mieux faire notre choix d’analyse ?

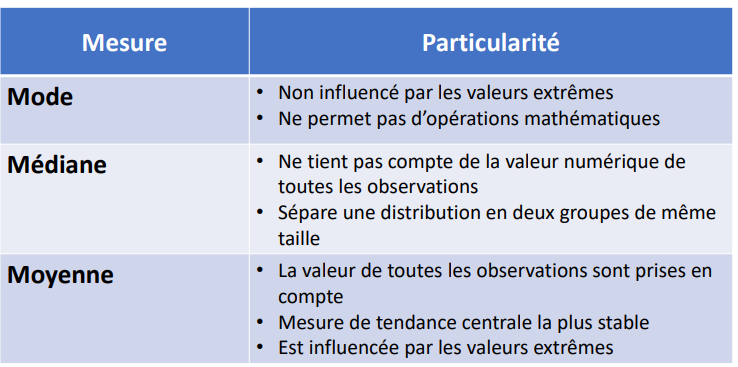
Mesures de position

Qu’est-ce qu’une mesure de position ?

Indique la place d’une valeur dans la distribution (c-à-d par rapport à la tendance centrale et la dispersion/écart-type).

quelles sont les 2 manières de mesurer la position par rapport à la moyenne ?

1. par groupe de %

2. par le score z

Quels sont les types de mesures par groupe de % ?

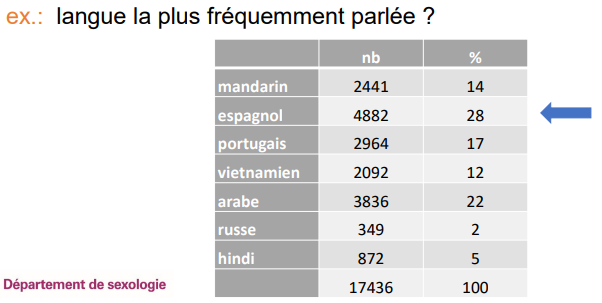
Centiles (1%), déciles (10%), quartiles (25%), quintiles (20%), terciles (33,3%).

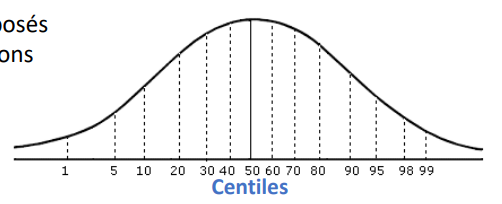
Quelle est la fonction de la mesure par groupe de %?

sert à voir si un individu/donnée X se situe dans quelle groupe de la distribution

Ex. : « pour mon test Casper, j'étais dans le 4e quartile de la distribution de tous les étudiants, ce qui veut dire que j'étais dans les 25% meilleur! »

Qu’est-ce qu’un score Z ?

Nombre d’écarts-types entre une valeur et la moyenne.

À quoi sert le score Z ?

À comparer des valeurs de distributions différentes (en les plaçant sur une même échelle standardisée)

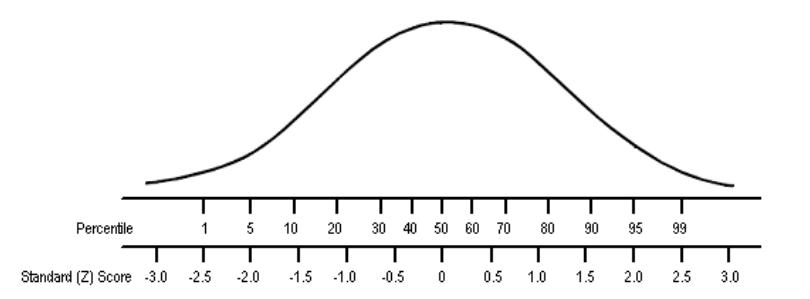
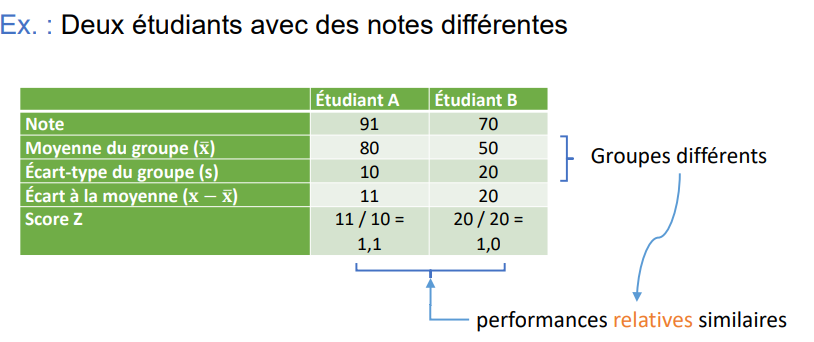
Le score Z permet de… 

comparer des réalités très différentes sur un pied d’égalité

ex : comparer des étudiants dont la performance est mesurée dans des contextes différents (ex. des évaluations dont le niveau de sévérité n’est pas le même)

ex : comparer la satisfaction sexuelle dans 2 études, étude A de 1-50 et étude B 1-15 → cote Z permet de voir à combien d'écart-type (même unité) les résultats sont de la moyenne = comparable

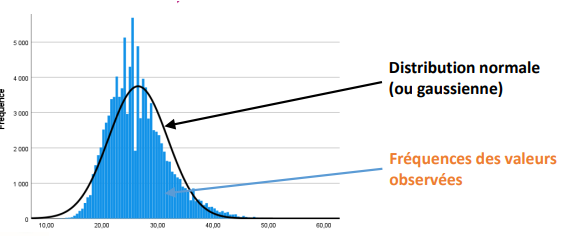
Distribution normale centrée réduite

Qu’est-ce qu’une distribution normale centrée réduite ?

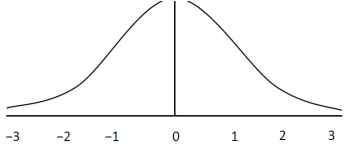
Courbe en cloche qui décrit la répartition théorique (statistique) des valeurs.

→ n’exprime pas les fréquences observées

Quelle est l’utilité de la distribution normale centrée réduite ?

permet de prévoir les probabilités de plusieurs phénomènes aléatoires + permet de calculer l'inférence (porter un jugement sur une population à partir d’un échantillon)

Quelles sont ses propriétés ?

• La moyenne est de 0

• L’écart-type est de 1

• 100% des événements possibles se trouve sous la courbe

• Elle est symétrique (50% événements ch. côté moy.)

• Les extrémités ne touchent jamais l’axe horizontal (mais l’essentiel de la courbe se trouve entre -3 et 3)

• Les points d’inflexion de la courbe sont à -1 et 1 (là où la courbe passe de concave à convexe)

Comment calcule-t-on une probabilité avec la distribution normale ?

En associant une probabilité à l’aire sous la courbe.

Interprétation de l'exemple : la probabilité d'une observation d'être entre 0 et 1,34 d'écart-type = 41% (déduit avec une table)