10.Hypothesis Testing

10.6.Sample size estimation

¿Cuál es la finalidad principal de la estimación del tamaño de la muestra (n) en la fase de planificación de un estudio?

Determinar el tamaño de la muestra necesario para proporcionar una potencia especificada a una prueba estadística.

¿Cuál es la hipótesis nula (H0​) planteada en el ejemplo de colesterol sérico para la estimación del tamaño de la muestra?

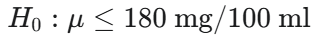
En el ejemplo del colesterol, ¿cuáles son los valores dados para el nivel de significancia (α) y la desviación estándar (σ)?

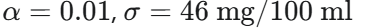
Si la verdadera media poblacional fuera 211 mg/100 ml, ¿qué probabilidad de falla en rechazar H0​ (error Tipo II, β) se desea en el ejemplo?

Una probabilidad del 5% de fallar en rechazar la hipótesis nula, lo que significa β=0.05 y una potencia (1−β) de 0.95.

Para α=0.01 en una prueba unilateral, ¿cuál es el valor crítico de z para rechazar H0​?

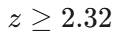
Expresión de la media muestral (xˉ) en términos de z cuando H0​:μ≤180 es verdadera.

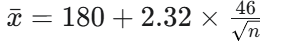
Si el verdadero nivel de colesterol es μ1​=211 mg/100 ml y deseamos una potencia de 0.95 (β=0.05), ¿cuál es el valor de z que corresponde a β=0.05?

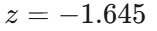
Expresión de la media muestral (xˉ) en términos de z cuando la verdadera media poblacional es μ1​=211 mg/100 ml.

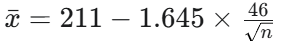
¿Cuál es el paso para resolver n una vez que se igualan las dos expresiones de xˉ?

¿Cuál es el tamaño de la muestra final requerido para el ejemplo de colesterol sérico después de redondear?

35 individuos (siempre se redondea hacia arriba).

¿Qué representan z1−α​ y z1−β​ en el contexto de la distribución normal estándar para calcular el tamaño de la muestra?

Expresiones generales para xˉ en un test unilateral (H0​:μ≤μ0​ vs H1​:μ>μ0​) basadas en z1−α​ y z1−β​.

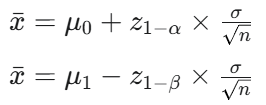
Fórmula general para el tamaño de la muestra (n) en un test unilateral (H0​:μ≤μ0​ vs H1​:μ>μ0​).

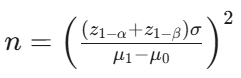
¿Cómo influyen los errores Tipo I y Tipo II en el tamaño de la muestra n?

Reducir el error Tipo I (α) aumenta n.

Reducir el error Tipo II (β) o aumentar la potencia (1−β) aumenta n.

¿Cómo influyen la diferencia entre las medias (μ1​−μ0​) y la variabilidad (σ) en el tamaño de la muestra n?

Una menor diferencia entre μ1​−μ0​ aumenta n.

Una mayor variabilidad (σ) aumenta n.

¿Cuándo se debe realizar un test de dos colas para la estimación del tamaño de la muestra en lugar de uno de una cola?

Cuando no se sabe si μ0​ es mayor o menor que μ1​.

En un test de dos colas con α=0.01, ¿cuál sería el valor crítico de z para rechazar H0​ (comparado con el 2.32 del unilateral)?

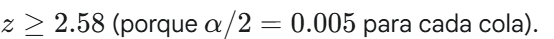
Fórmula general para el tamaño de la muestra (n) en un test de dos colas.

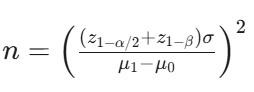
¿Cómo se compara el tamaño de la muestra para un test de dos colas con el de un test de una cola correspondiente?

El tamaño de la muestra para un test de dos colas siempre es más grande que el de una cola.

¿Cuál es la regla universal para redondear el tamaño de la muestra (n) obtenido de los cálculos?

Siempre redondear n hacia arriba al entero más cercano.

En la derivación del tamaño de la muestra, después de igualar las expresiones para xˉ, ¿cuál es el primer paso algebraico para agrupar términos relacionados con n?

Mover los términos con n​ a un lado y los términos constantes al otro:

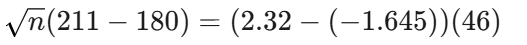
Continuando la derivación del tamaño de la muestra del ejemplo de colesterol, ¿cuáles son los valores numéricos de la diferencia de medias y la suma de los valores z?

Diferencia de medias: 211−180=31 Suma de z: 2.32−(−1.645)=2.32+1.645=3.965

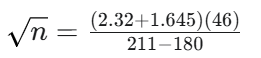
En la derivación de la fórmula del tamaño de la muestra, ¿por qué es importante el signo negativo de z1−β​ (como en z=−1.645 para β=0.05)?

Porque la media muestral (xˉ) para el cálculo de la potencia (μ1​) está a la izquierda de la verdadera media μ1​, en la cola inferior de la distribución de la media muestral.

¿Qué representa la diferencia (μ1​−μ0​) en las fórmulas de tamaño de la muestra?

La magnitud de la diferencia que el investigador desea detectar o la "magnitud del efecto" mínima que se considera clínicamente o prácticamente significativa.

Si la variabilidad de los datos (σ) es desconocida al inicio del estudio, ¿qué métodos se pueden usar para obtener una estimación y así calcular n?

1. Usar datos de estudios piloto.

2. Usar datos de estudios previos similares.

3. Estimarla a partir del rango de datos esperados (ej. rango / 4 o rango / 6).

¿Cuál es el impacto en el tamaño de la muestra (n) si deseamos una mayor confianza (es decir, reducir α de 0.05 a 0.01)?

Un nivel de significancia (α) más pequeño (ej. 0.01) requiere un valor z1−α​ mayor, lo que a su vez aumenta el tamaño de la muestra (n).

¿Cuál es el impacto en el tamaño de la muestra (n) si deseamos una mayor potencia (es decir, aumentar 1−β de 0.80 a 0.95)?

Una mayor potencia (1−β) implica un valor β más pequeño (ej. 0.05), lo que requiere un valor z1−β​ mayor, y en consecuencia aumenta el tamaño de la muestra (n).

¿Por qué la fórmula del tamaño de la muestra para un test de dos colas usa z1−α/2​ en lugar de z1−α​?

Porque el nivel de significancia (α) se divide entre las dos colas de la distribución (por ejemplo, 0.005 en cada cola para α=0.01), por lo que el valor crítico de z es mayor.

Si un estudio utiliza un test de dos colas y luego se descubre que solo interesaba detectar una diferencia en una dirección, ¿qué implicación tiene esto sobre el tamaño de la muestra utilizado?

El tamaño de la muestra fue innecesariamente grande (y por lo tanto, el estudio fue más costoso o requirió más participantes de lo necesario) porque los tests de dos colas siempre requieren un n mayor que los de una cola para la misma potencia y nivel de significancia.