Gain, Phase-lag, and Phase-lead Compensation in Control Systems

Dynamic performance

Relates to transient response characteristics such as rise time, settling time, and overshoot, defining how the system reacts to changes or disturbances.

Steady-state performance

Refers to the system's ability to eliminate errors in the long term and maintain stability around a desired operating point.

Compensator

An additional algorithm or component inserted into a control system to compensate for a deficient performance.

Gain compensator

The simplest form of compensator that amplifies the error signal by introducing a proportional gain K.

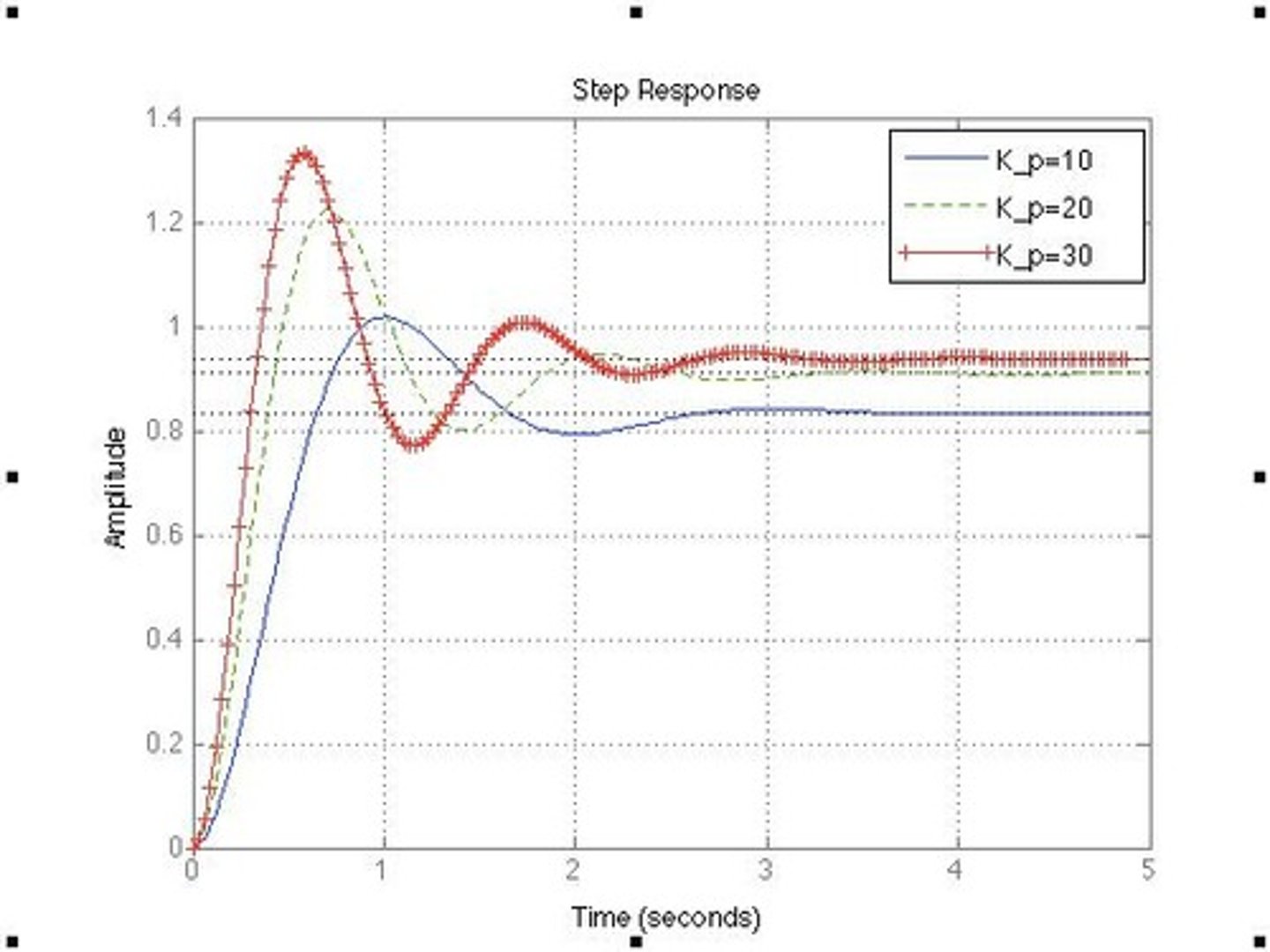
Proportional gain K

The gain introduced by a gain compensator that alters the magnitude of the system's response.

Phase-lag compensator

Introduced to address deficiencies in steady-state performance, such as high steady-state error, by modifying system dynamics.

Pole and zero in phase-lag compensator

A pole is placed closer to the origin of the complex plane than the zero to improve tracking of reference inputs or rejection of disturbances.

Phase-lead compensator

Used for systems with deficiencies in dynamic performance, enhancing transient response by providing a phase advance/lead.

Ideal phase-lead

Accomplished by introducing a zero (or both a zero and a pole) with the zero located to the left of the pole in the complex plane.

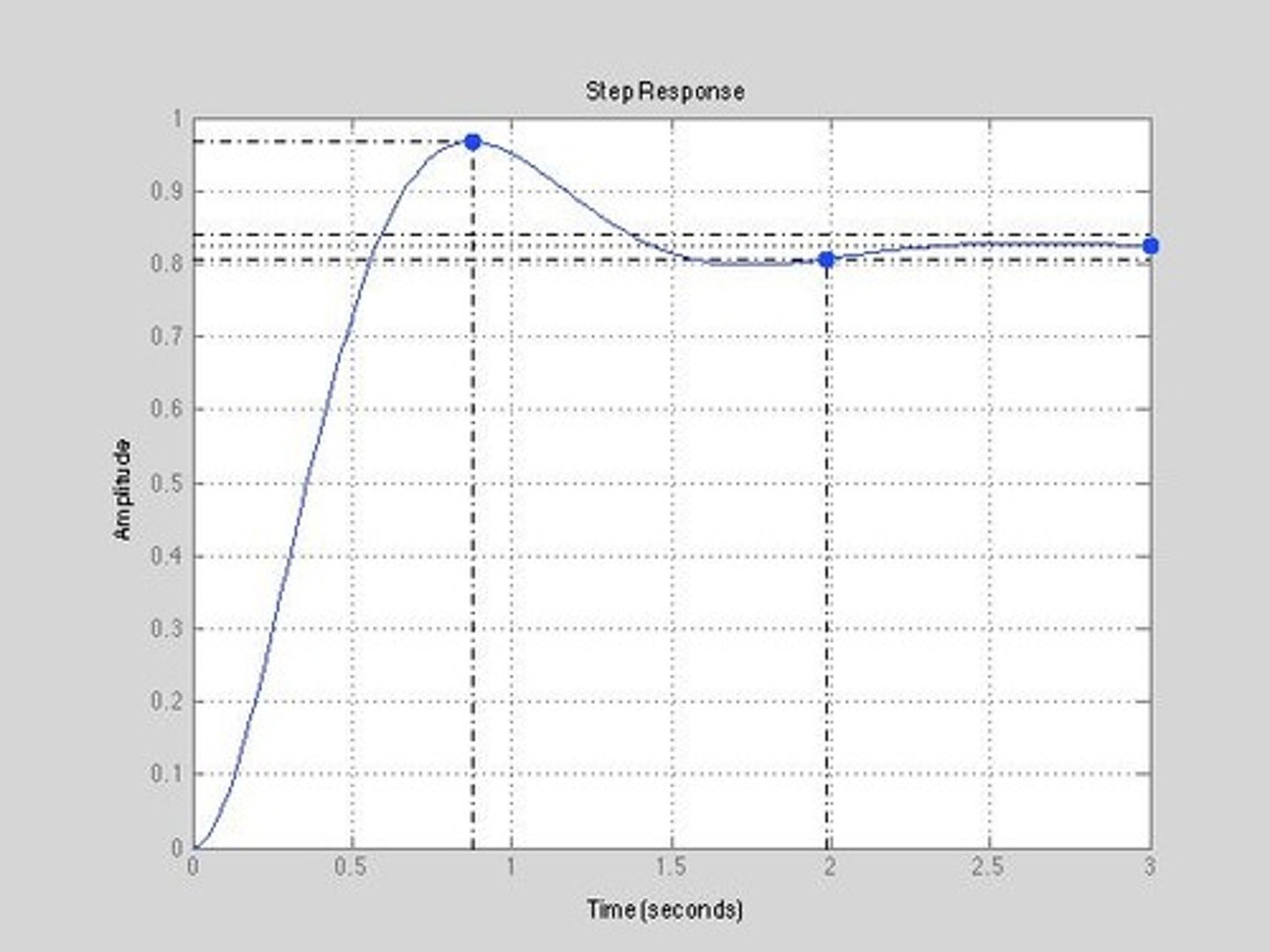
Transient response characteristics

Include rise time, settling time, and overshoot, which define how the system reacts to changes or disturbances.

High steady-state error

A deficiency in steady-state performance that can be addressed by a phase-lag compensator.

Slow rise times

A deficiency in dynamic performance that can be improved by using a phase-lead compensator.

High overshoot

A deficiency in dynamic performance that can be improved by using a phase-lead compensator.

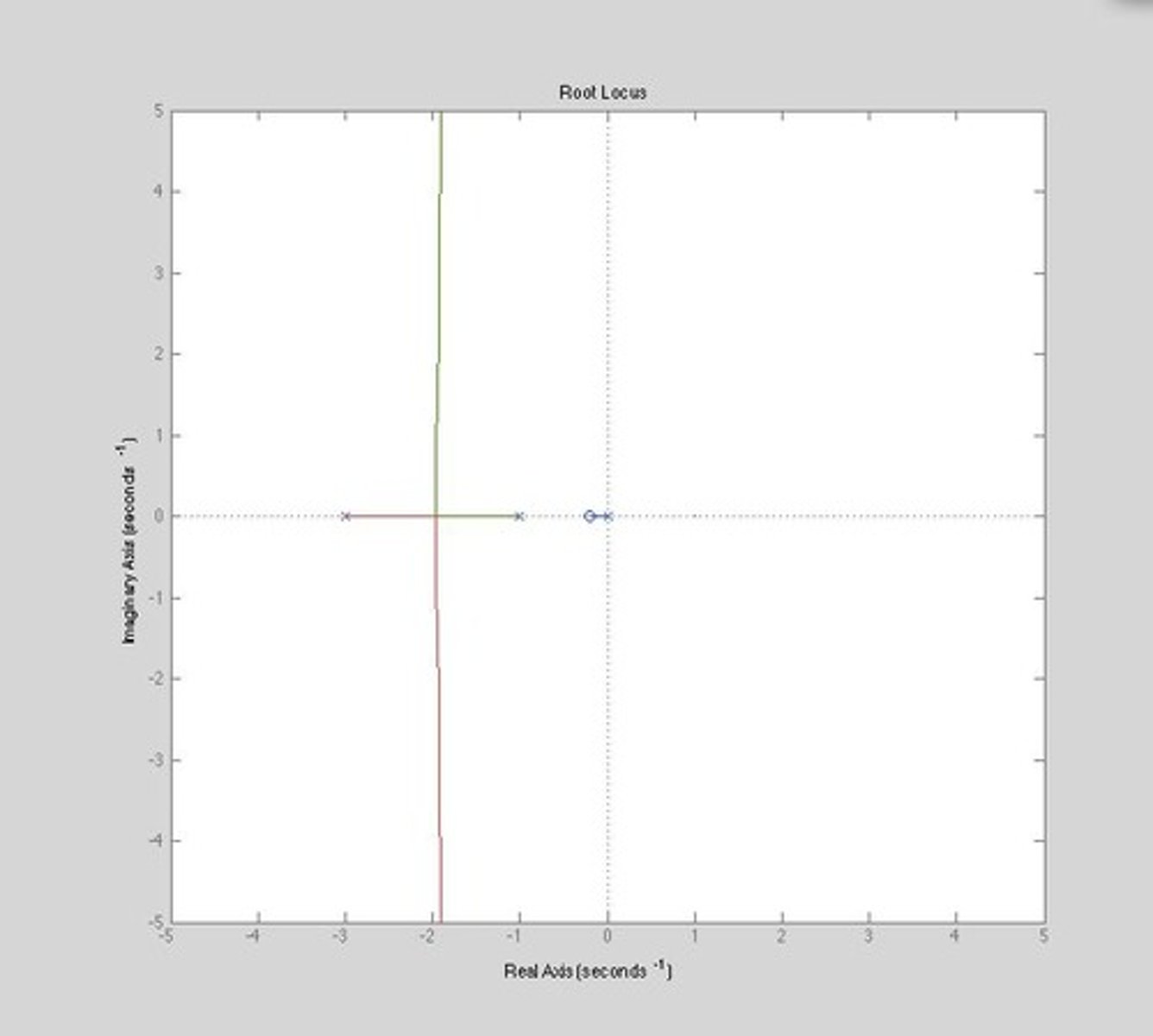
Closed-loop poles

Locations in the root locus that can be altered by adjusting the value of K in a gain compensator.

Root locus

A graphical representation of the locations of closed-loop poles as a system parameter is varied.

Trade-offs in compensators

Careful consideration is needed to balance improving steady-state accuracy and maintaining acceptable dynamic performance.

System dynamics

Inherent limitations that may prevent a simple closed-loop control design from satisfying all required performance specifications.

Performance specifications

Typically divided into dynamic performance and steady-state performance.

Amplification in gain compensator

Alters the magnitude of the system's response without changing the root locus itself.

Compensator limitations

A gain compensator cannot modify the structure or trajectory of the root locus.

Phase lag introduction

Occurs in a phase-lag compensator, which may negatively impact transient response characteristics.

Favourable locations of closed-loop poles

Achieved by the phase-lead compensator to improve the speed and stability of the system response.

Lead-Lag Compensator

A compensator used when a control system exhibits both steady-state and dynamic performance deficits, combining the effects of phase-lead and phase-lag compensators.

Transient Response

The response of a system to a change in input that occurs before reaching steady-state.

Steady-State Accuracy

The ability of a control system to maintain a desired output level over time after transient effects have settled.

Poles and Zeros

Elements in the transfer function of a system that determine the system's behavior and stability.

Bode Plot

A graphical representation of a system's frequency response, showing gain and phase shift as functions of frequency.

Nyquist Plot

A graphical representation of a system's frequency response that helps assess stability and performance.

Simulation

A tool used to visualize the effects of compensator design choices and optimize system response.

Gain Compensation

A technique in control system design that introduces a proportional gain K to adjust closed-loop behavior.

Closed-Loop Behavior

The behavior of a control system when feedback is applied to regulate its output.

Damping Ratio (ζ)

A parameter that describes how oscillations in a system decay after a disturbance.

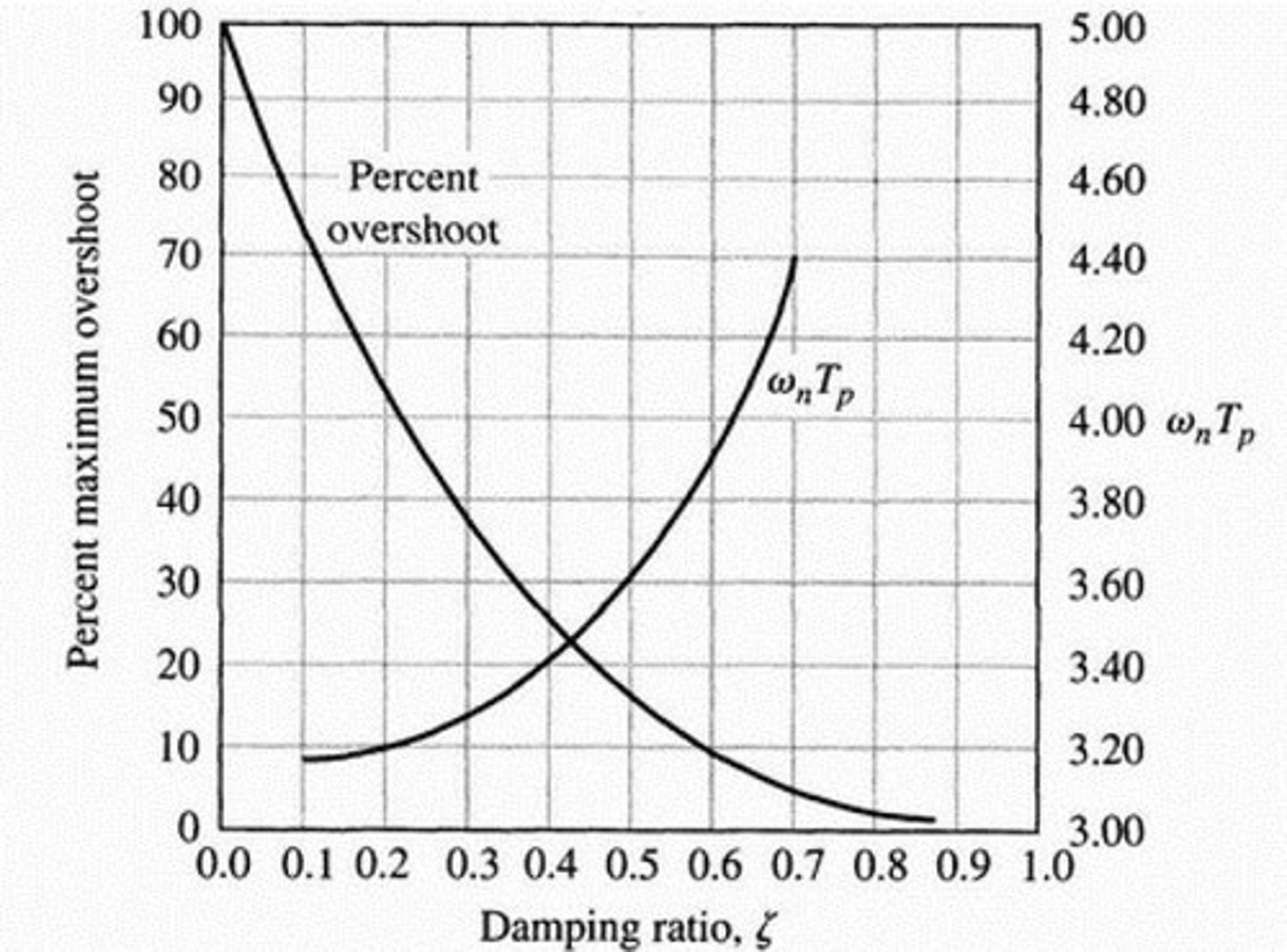
Natural Frequency (ωn)

The frequency at which a system oscillates when not subjected to any damping or external force.

Settling Time

The time required for a system's response to settle within a specified range of the final value after a disturbance.

Rise Time

The time taken for a system's response to rise from a specified low value to a specified high value.

Overshoot

The extent to which a system's response exceeds its final steady-state value.

Transfer Function G(s)

A mathematical representation of a system's input-output relationship in the Laplace domain.

Performance Deficits

Shortcomings in a control system's ability to meet specified performance criteria.

Iterative Adjustments

The process of making successive refinements to a design based on feedback and analysis.

Complex Real-World Demands

Challenges that control systems must meet in practical applications, requiring robust and reliable designs.

Magnitude Criterion

The product of the magnitudes of all vectors from the poles of G(s)H(s) to the point on the s-plane, divided by the product of the magnitudes of all vectors from the zeros of G(s)H(s) to the same point, must equal K.

Gain K

The value determined using the magnitude criterion of the root locus.

Poles

The values represented by pi in the context of the transfer function G(s)H(s).

Zeros

The values represented by zj in the context of the transfer function G(s)H(s).

Steady-State Error (SSE)

The significant error that exists in a control system that cannot be resolved using a simple gain compensator.

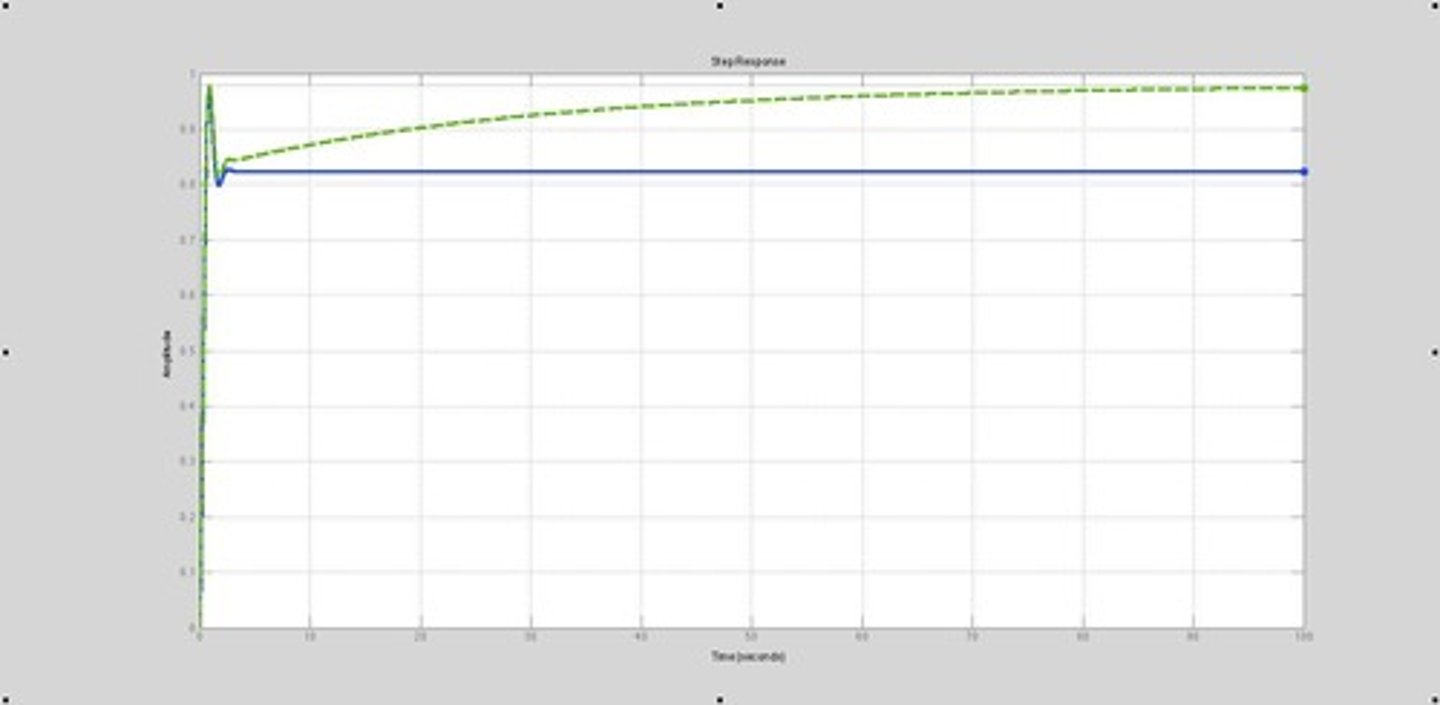
Phase-Lag Compensation

A method primarily used to improve the steady-state performance of a control system.

Final Value Theorem

A theorem that connects the steady-state value of a system to its transfer function in the Laplace domain.

Ideal Phase-Lag Compensator

A compensator represented by the transfer function D(s) = Kc / (s + zc) s, where Kc is the compensator gain.

Compensator Gain (Kc)

The gain associated with the ideal phase-lag compensator.

Compensator Pole

The pole of the compensator, ideally placed at the origin to eliminate steady-state error.

Compensator Zero (zc)

The zero of the ideal phase-lag compensator, placed as close to the origin as possible.

Practical Phase-Lag Compensator

A compensator represented by the transfer function D(s) = Kc / (s + zc)(s + pc), where the compensator pole is not constrained to the origin.

Ratio R

Defined as R = zc / pc, which determines the compensator's ability to meet the required SSE.

Transient Dynamics

The behavior of a control system during the time period when it is responding to a change in input.

Control System Design

The process of creating a control system that meets specified performance criteria.

Iterative Simulations

The process of refining the value of K through repeated testing and adjustments.

Additional Compensators

Compensators such as phase-lead or phase-lag compensators that may be required if a gain compensator alone is insufficient.

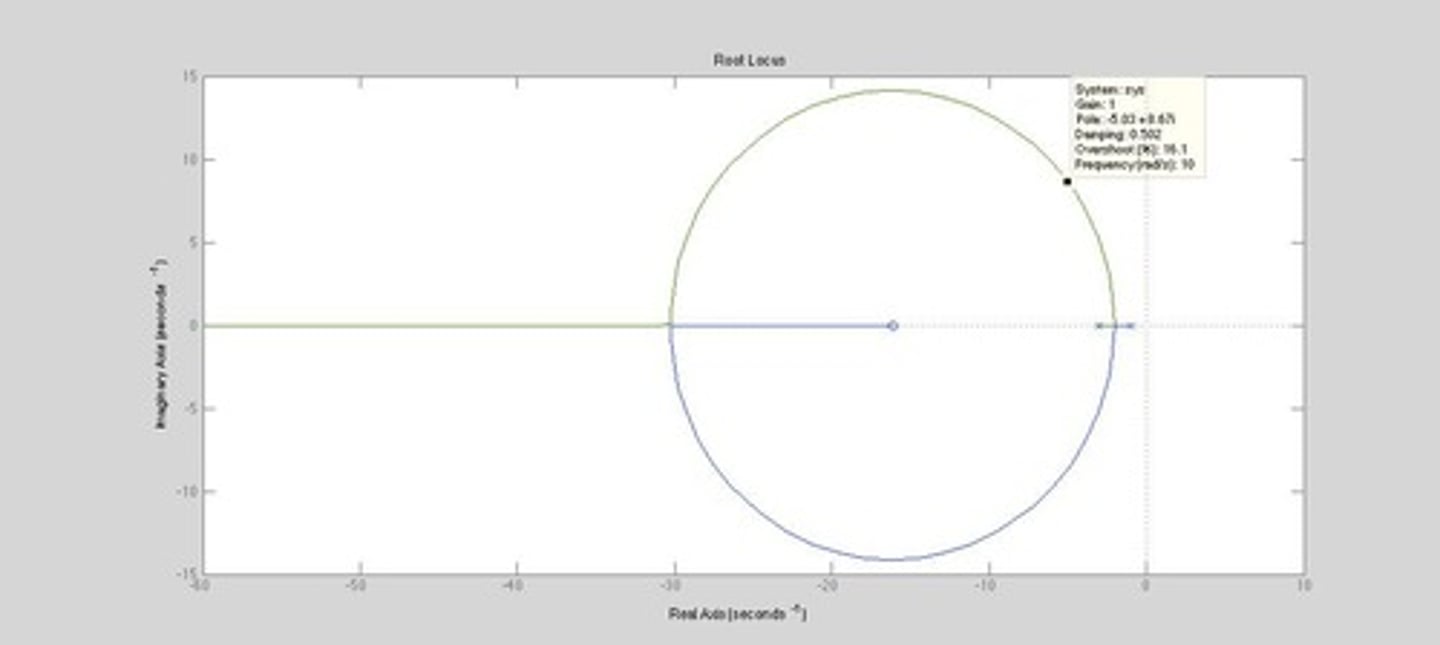
Example 4.1

An illustrative example of gain compensator design applied to a specific control system.

Dominant Pole

The pole (or poles) of a system's transfer function that has the most significant impact on the system's overall response, particularly its transient behaviour.

Real Part of Dominant Pole

The smallest negative real parts among all the system's poles, closest to the imaginary axis in the complex s-plane.

Compensator Pole (pc)

Calculated using the predefined ratio R as pc = zc / R.

Trade-offs in Compensator Design

Balancing between improving steady-state accuracy and maintaining acceptable transient response.

Low-Frequency Gain

A parameter calculated using the final value theorem in the context of compensator design.

Phase-Lead Compensation

An effective method to enhance the dynamic performance of a control system when gain compensation alone cannot meet the desired specifications.

Dynamic Specifications

Parameters such as overshoot, rise time, and settling time that require precise adjustments to the system's response.

Phase-Lead Compensator Transfer Function

Represented by D(s) = Kc(s + zc), where the zero zc modifies the root locus trajectory.

Angle Criterion

Applied to determine zc, ensuring that the compensator zero contributes the necessary phase advance at the desired closed-loop pole location.

Ideal Phase-Lead Compensator

Straightforward and effective for theoretical designs but rarely used in practice.

Transient Behaviour

The response of a system to a change in input, characterized by how quickly it reaches a steady state.

Steady-State Error

The difference between the desired output and the actual output of a system once it has settled.

Compensator's Parameters

Tuned to achieve the desired balance between steady-state and transient performance.

Practical Considerations in Compensator Implementation

Ensuring that the compensator provides robust performance while being cost-effective and feasible to implement.

Example 4.4

An illustrative example of phase-lag compensator design applied to a specific control system.

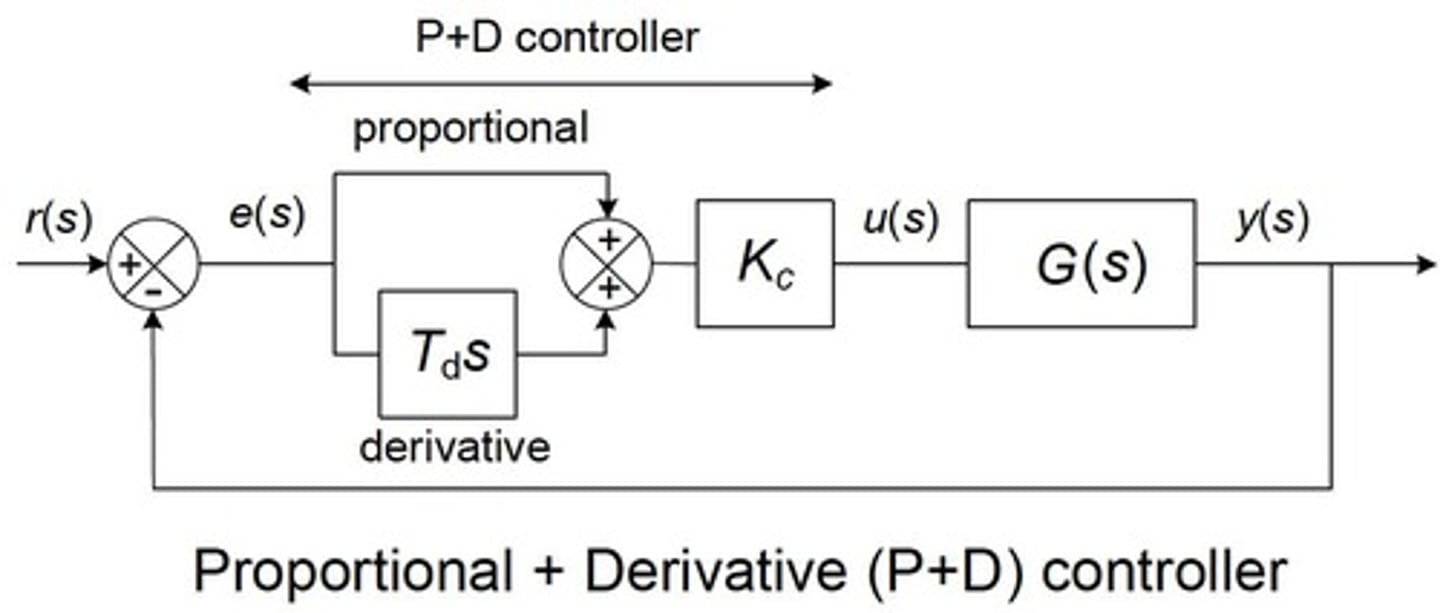
Proportional-Derivative (PD) Controller

A control system that is highly sensitive to step changes in input and prone to amplifying high-frequency noise.

Transfer Function

The mathematical representation of the relationship between the input and output of a system, denoted as D(s)G(s) for a typical third-order system.

Design Rules for zc Placement

Guidelines that suggest placing the compensator zero anywhere between -3 (exclusive) and -5 (inclusive) for optimal performance.

Example 4.6

An example in the lecture that illustrates the placement of the compensator zero, where zc = 4 was chosen to demonstrate the standard application of the angle criterion.

Second-Order System Approximation

An assumption made during the design process that simplifies the system by neglecting the effects of remaining poles, treating it as a second-order system.

Dominant Poles

The poles of a system that have the most significant impact on its transient response and are maintained near their original locations by the compensator.

Sequential Design Approach

A method of designing a lead-lag compensator where the phase-lead compensator is designed first to meet dynamic performance specifications.

Fixed Angle Contribution

The angle contribution of 90 degrees at the desired location when zc = 5, which simplifies calculations in compensator design.

Simulation Validation

The process of verifying the final design of a compensator through simulations or software tools to ensure it meets performance criteria.

Phase Condition

The requirement that the total angle contribution at the desired root locus point must satisfy specific criteria for stability and performance.

Control Design

The process of creating a control system that meets specified performance criteria, often involving the use of compensators.

Approximation Errors

Errors introduced in the design process when simplifying a system to a second-order model, necessitating further validation.

Performance Criteria

The standards that a control system must meet in terms of stability, transient response, and steady-state accuracy.

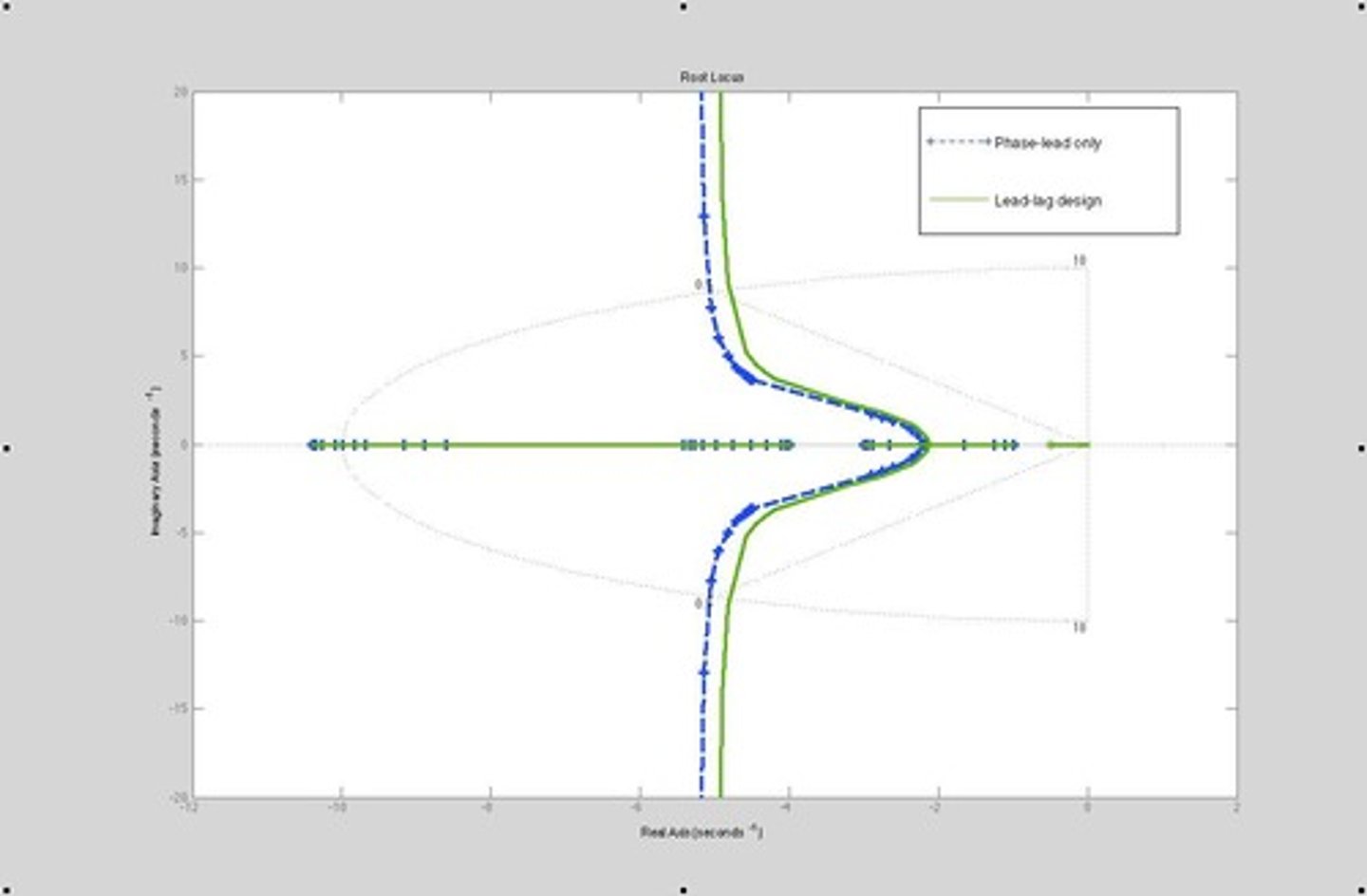
Sequential lead-lag design

A method that involves designing a phase-lead compensator followed by a phase-lag compensator to achieve desired transient and steady-state performance.

Closed-loop pole locations

The positions of the poles of a control system when feedback is applied, which determine system stability and response characteristics.

Sequential lag-lead design

A design approach where the phase-lag compensator is designed first, followed by the phase-lead compensator, to minimize interaction between them.

Dominant Pole Approximation

An assumption in control system design that non-dominant poles have negligible effects on transient behavior, allowing the system to be approximated as a second-order system.

Root Locus Interaction

The combined effect of phase-lead and phase-lag compensators on the root locus, where the phase-lead pulls it to the left and the phase-lag shifts it to the right.

Frequency Range Separation

The practice of designing phase-lead and phase-lag compensators to operate in different frequency ranges to minimize their interaction.

Phase margin

A measure of stability in control systems, defined as the amount of additional phase lag at the gain crossover frequency that will lead to instability.

Ideal phase-lag compensators

Compensators designed with a pole at the origin and a zero near the origin to reduce steady-state error without significantly affecting transient response.

System behaviour

The overall response characteristics of a control system, influenced by the placement of poles and zeros.

Design error

The discrepancy that arises during the design process, often due to approximations made in modeling the system.

Simulation tools

Software or methods used to validate and correct design errors in control systems through modeling and analysis.

Mid-to-high-frequency range

The frequency range where the phase-lead compensator operates to enhance transient response.

Low-frequency range

The frequency range where the phase-lag compensator operates to increase low-frequency gain and reduce steady-state error.

Compensation

the alternation or adjustment of a control system in order to provide more suitable performance.