Refraction & Vergence

Use the concept of vergence at plane and curved surfaces in calculations for image position, magnitude, orientation and use and understand the concept of refraction in optical applications

Refraction and Refractive Index

• Refraction is the change in direction of a light wave due to a change in its velocity

  • Imagine a glass of water with a pencil inside (picture): The pencil seems to bend at the water surface. Reason for this effect: air and water have different refractive indices and thus, cause the velocity of light to change

• Meaning of refractive index (n): It is the ability of a medium to slow light down in a transparent material.

  • n = speed of light in a vacuum / speed of light in medium

• n in air : n_air = 3 × 10⁸ m/s / 3 × 10⁸ m/s = 1

Refractive index (n) is the ability of a medium to ___________ down in a transparent material.

Slow light

Refractive Index ‘n’ (Also Abbreviated as RI)

• How is “n” determined?

• White light consists of many different wavelengths, each of which is slowed down at a different rate (affecting n)

• To overcome this issue: “n” is given for specified spectral lines in the ISO 7944:

  • UK: 587.562 nm (Helium ‘d’ line)

  • France & Germany: 546.073 nm (Mercury ‘e’ line)

• Because these correspond closely to the wavelength the human eye is most sensitive to in daylight (photopic) conditions 555nm

___________ consists of many different wavelengths, each of which is slowed down at a different rate (affecting n).

White light

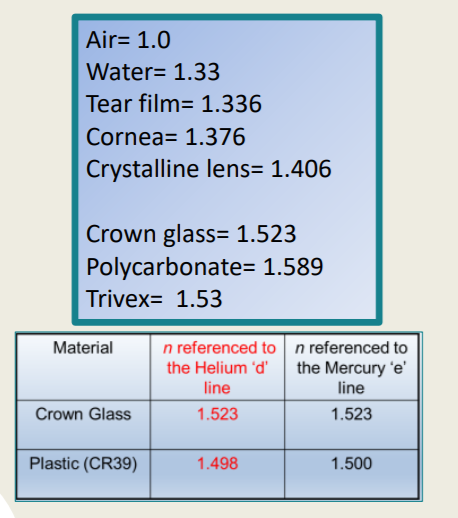
Refractive Indices to Remember

• Typical refractive indices (n) used in Optometry are:

  • Air =1.0

  • Water = 1.33

  • Tear Film = 1.336

  • Cornea = 1.376

  • Crystalline Lens = 1.406

  • Crown Glass = 1.523

  • Polycarbonate = 1.589

  • Trivex = 1.53

• Nevertheless, be careful when reading manufacturer’s technical data to decide on appropriate lens materials.

For plastic (CR39), ‘n’ referenced to the Helium ‘d’ line is ________ and ‘n’ referenced to the Mercury ‘e’ line is ________.

1.498; 1.500

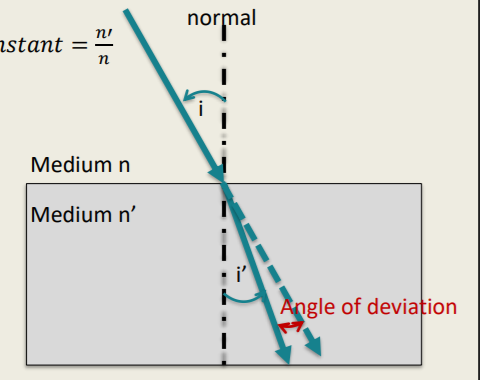
Laws of Refraction

• The incident (i) and refracted (i’) light rays lie in one plane which is normal to the refracting surface at the point of refraction

• The ratio of the sine of the angle of incidence (i) to the sine of the angle of refraction (i’) is a constant.

• This is called Snell’s Law (Snell 1580-1626) : sin 𝑖 / sin 𝑖′ = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 = 𝑛′/ n

A __________ is the ratio of the sine of the angle of incidence (i) to the sine of the angle of refraction (i’).

Constant

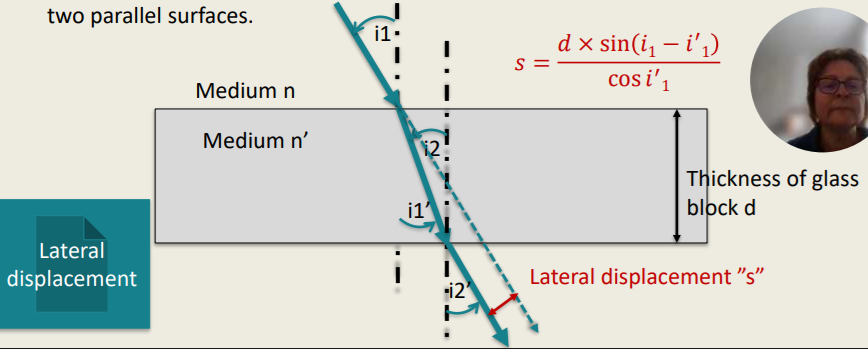
Refraction on Plane Surfaces - Glass Block

• Laws of Refraction:

  • Incident, refracted light ray and normal to the surface are in one plane

  • Snell’s law: 𝒏 × 𝐬𝐢𝐧 𝒊 = 𝒏′ × 𝐬𝐢𝐧 𝒊′

• The laws of refraction apply on each surface. Thus, in case of two surfaces (e.g. lenses, glass block), they apply twice.

• The light ray emerging from the block does not change direction, but it “jumps”. This jump is called lateral displacement (s) and, it happens when light is refracted through two parallel surfaces.

The laws of refraction apply on each surface. True or False?

True

Refraction on Plane Surfaces - ‘Total Internal Reflection’

• When a light ray enters a transparent medium (e.g. water or glass) at a certain angle – the critical angle “i_c” – total internal reflection occurs.

• Application of total internal reflection: fibre optics (cables) , Sclerotic Scatter (Slit Lamp technique)

• Total reflection depends upon two aspects:

  • Refractive index difference (n’-n) between both media; n_fibre > n_environment

  • Angle of incidence i at the surface; i > i_c

When a light ray enters a transparent medium (e.g. water or glass) at a certain angle – the _________ “i_c” – total internal reflection occurs.

Critical Angle

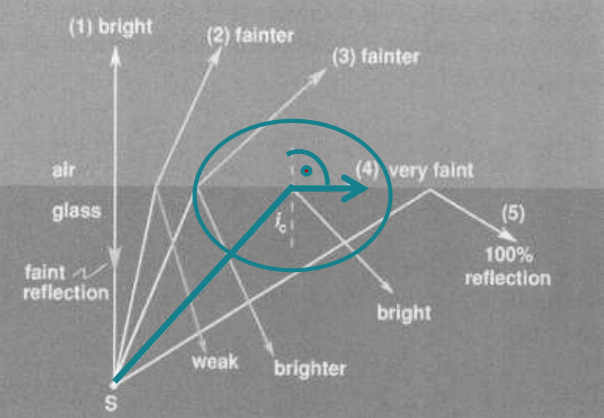
Refraction on Plane Surfaces - Total Internal Reflection - Critical Angle (i_c)

• Determining the critical angle for two materials:

  • Snell’s law: 𝑛 × sin 𝑖 = 𝑛′ × sin 𝑖′

  • From the graphic: The critical angle – no refraction - occurs in ray 4 and from the drawing we see that i’= 90°

• Apply 2 in 1:

  • 𝑛_{𝑚𝑒𝑑𝑖𝑢𝑚} × sin 𝑖_𝑐 = 𝑛_𝑎𝑖𝑟 × sin 90°

• because sin 90^o = 1 we can rearrange above equation to:

  • 𝐬𝐢𝐧 𝒊_𝒄 = 𝒏_𝒂𝒊𝒓 / 𝒏_{𝒎𝒆𝒅𝒊𝒖𝒎} ; 𝒂𝒏𝒅 𝒊_𝒄 = sin−𝟏 (𝒏_𝒂𝒊𝒓 / 𝒏_{𝒎𝒆𝒅𝒊𝒖𝒎}) = sin^−𝟏 (𝒏′ / 𝒏)

• Knowing this, you can calculate the critical angle for two materials. Important: n’ < n.

You can calculate the __________ for two materials.

Critical Angle

Refraction on Plane Surfaces - ‘Reduced Optical Thickness’

• When light is incident on a denser (transparent) medium you will have noticed that things seem to be closer (d) than they truly are (t) in an optically denser medium.

• Refers to reduced optical thickness “d” and is calculated as follows: 𝑑 = 𝑡 / 𝑛

• Application: Calculation for thick lenses

d = t /______

n - Refractive index

Refraction on Curved Surfaces - Principle of Vergence

• Consider: light rays (“pencils”) travel in a straight line through a homogenous medium. A collection of pencils is called beam of light.

• Vergence describes the path of the “pencil” of light rays.

• Vergence is given the symbol L, and the units are dioptres D [equivalent to m-1 ]

• One D is the vergence in a pencil of light rays in air (n=1) at a point one metre to the light source or focus 𝐋 = 𝟏 / 𝐥 with l being the distance from the object , and l’ from the image in [m]

• Three types:

  • Converging pencils: L= positive D

  • Diverging pencils: L= negative D

  • Parallel pencils of rays from a source or object in infinity: L= 0D

A collection of _________ is called a beam of light.

Light Rays or Pencils

Example Calculation

• A divergent light ray in air from a source (S) 25 cm away enters a lens. The lens adds 6.00D of convergence to the incident ray. Where will the focus form?

• One D is the vergence in a pencil of light rays in air (n=1) at a point one metre to the light source or focus 𝐋 = 𝟏 / 𝐥 with l being the distance from the object , and l’ from the image in [m]

• Unit for L is D= m^-1 and thus l = -25 cm has to be converted into m: -25cm = -0.25m

• 𝐿= 1/𝑙 L= -1/0.25m = -4.00D

• The lens adds +6.00D (convergence means +) to L resulting in L’= -4.00D + 6.00D = +2.00D

• Hence, the focus forms at the distance l’= 1 / L’ = 1/ +2.00D = +0.5mm (cross multiply to make this equation from the L = 1/ I)

What is the answer?

The answer is: the focus forms 0.5m (or 50cm) to the right of the lens (+sign means convergence)

Refraction of Curved Surfaces

• Vergence describes the path of a ray of light and thus, it is directly linked with refraction.

• Terminology:

  • C = Centre of curvature of refracting surface

  • I = Vergence distance of incident light

  • I’ = Vergence distance of emergent light

• Incident vergence (L) added to the surface power (F) to determine the emergent light vergence distance (l’)

• Surface Power: F = (𝒏′−𝒏) / 𝒓 and 𝑭 = 𝑳 ′ − 𝑳

• Incident Vergence: L = n / i

• Emergent Vergence: L’ = n’ / i’

• These equations can be applied onto as many surfaces as there are, which is generally named “Raytracing”; in Optometry this method is also called “Step-along-method”

• It can be carried out mathematically and graphically.

Raytracing is also called the ___________ method in optometry.

Step-along-method

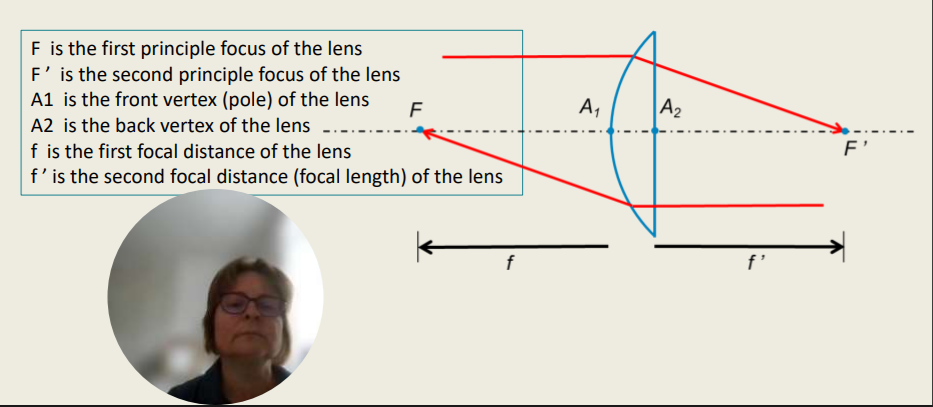
Refraction on Thin Lenses - Terminology

• A lens (thin or thick) consists of two refracting surfaces.

• The unit of lens power (F) is called the Dioptre.

• F is given by the equation: 𝐅=𝐧/𝐟′ with l’=f’ in metres for an incident vergence of 0.

• In air this equation can be substituted to 𝐅=𝟏/𝐟′

• F is the first principle focus of the lens

• F ’ is the second principle focus of the lens

• A1 is the front vertex (pole) of the lens

• A2 is the back vertex of the lens

• f is the first focal distance of the lens

• f ’ is the second focal distance (focal length) of the lens

A lens consists of _______ refrcting surfaces.

Two

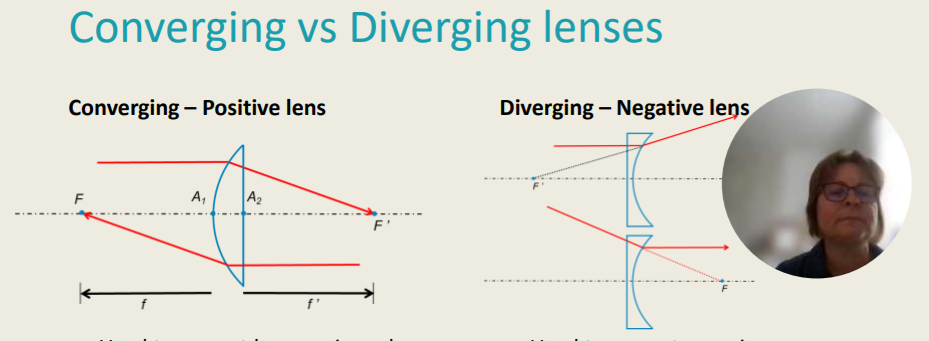
Converging vs Diverging Lenses

• Converging Lens (Positive lens)

  • used to correct hyperopia and presbyopia

  • Positive Lenses are thickest at the centre and thinnest at the lens edge

  • Lenses can be: biconvex, plano convex, and convex meniscus

• Diverging Lens (Negative Lens)

  • Used to Correct Myopia

  • Negative lenses are thickest at the edge and thinnest at the center

  • Lenses can be: Biconcave, plano concave and concave meniscus

________ lenses are used to correct myopia and ______ lenses are used to correct hyperopia and presbyopia.

Diverging (Negative Lenses); Converging (Positive Lenses)

Specifications in Optometry

• In optometry, we normally specify lens power to two decimal places.

• Spectacle prescriptions are issued in 0.25 D steps and the sign must be specified (+ or -)

• A lens with no focal power is termed a plano lens, which is either written “plano” or “∞”

A ______ lens has no focal power.

Plano

Thin Lenses - Vergence Calculations

• A thin lens is one in which the thickness (between both surfaces) is considerable negligible and, so can be ignored.

• For a thin lens, the power is equal to the sum of surface powers. 𝑭 = 𝑭_𝟏+𝑭_𝟐

• For a thin lens in air (n=1), the image position can be deduced mathematically using the known vergence equations.

  • Incident Vergence: 𝑳 = 𝟏 / 𝒍

  • Emergent Vergence: 𝑳′ = 𝟏 / 𝒍′ and 𝑭 = 𝑳 ′ − 𝑳

Example: Where will the image form if an object is placed 40 cm in front of a thin lens of power +6.00 D?

How I calculated the answer:

• Conversion:

  • 40cm to m = -40 × 0.01 = -0.4m

• Incidence Vergence:

  • L = 1 / -0.4 m = -2.50 D

• Emergent Vergence:

  • L' = F + L

  • L’ = +6.00 D - 2.50 D = +3.50 D

• Converting Vergence Into Vergence Distance:

  • L’ = 1 / i’ → I’ = 1 / L’

  • I’ = 1 / L’ = I’ = 1 / 3.50 (1/m) = + 0.286m

  • Answer = 28.6cm

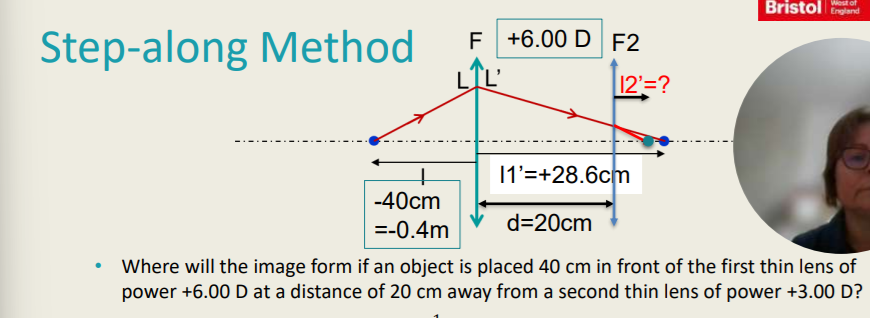
Step-Along Method

Example Question: Where will the image form if an object is placed 40 cm in front of the first thin lens of power +6.00 D at a distance of 20 cm away from a second thin lens of power +3.00 D?

Answer:

• L1

  • Conversion:

    • 40cm to m = -40 × 0.01 = -0.4m

  • Incidence Vergence:

    • L1 = 1 / -0.4 m = -2.50 D

  • Emergent Vergence:

    • L1' = F + L

    • L1’ = +6.00 D - 2.50 D = +3.50 D

• Transition L1 to L2:

  • i2 = (L1’- d)

  • L2 = n / i2 → L2 = 1 / (0.286m-0.20m)

  • L2 = +11.63D

• L2

  • Emergent Vergence:

    • L2' = F2 + L2 = +3.00 D + +11.63 D = +14.63 D

  • Convergent Emergence:

    • L2’ = 1 / i2’ → i2’ = 1 / L2’

    • i2’ = 1 / 14.63 (1/m) = +0.0683 m

    • Final answer = +6.8cm

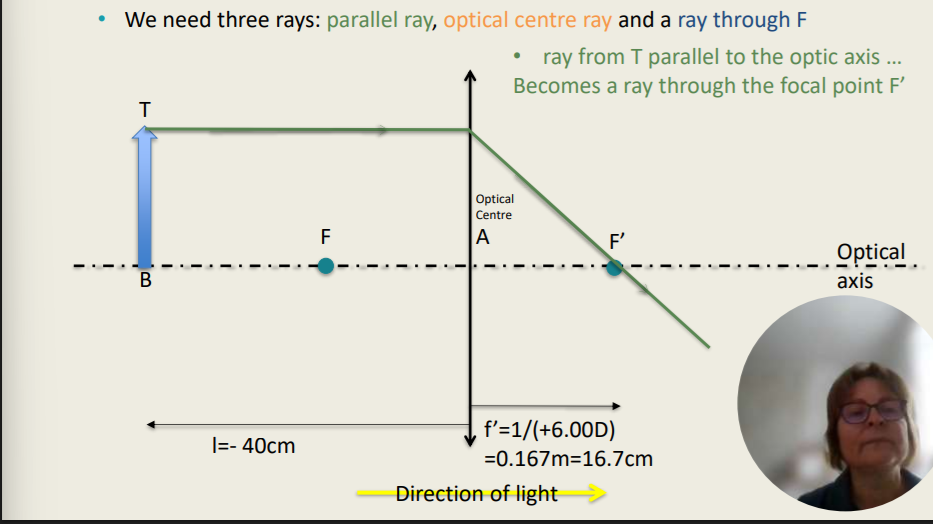
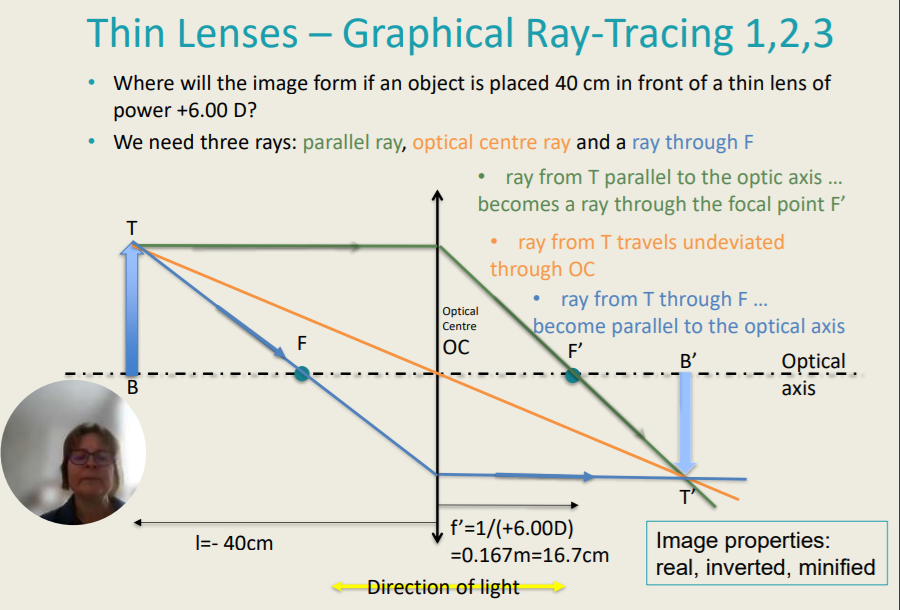
Refraction on Thin Lenses - Graphical RayTracing 1, 2, 3

We need three rays:

• Parallel ray (T), optical centre ray (A), and a ray through (F)

• A ray from T parallel to the optic axis becomes a ray through the focal point F’

Where will the image form if an object is placed 40 cm in front of a thin lens of power +6.00 D?

How I Calculated the Answer:

• F = n / f’ → f’ = n / F

• f’ = 1 / (+6.00) = 0.167m

• Final answer: 16.7cm

Application in Optometry (One Example)

• Binocular Indirect Ophthalmoscopy (BIO):

  • A head mounted light source is used and a +20 D or + 30 D lens

  • Distances determine image size and handling comfort

  • Image will be inverted

These calculations have applications in clinical practice for ________.

Slit Lamp BiO

Calculation for Yourself and Check Answers in the Seminar:

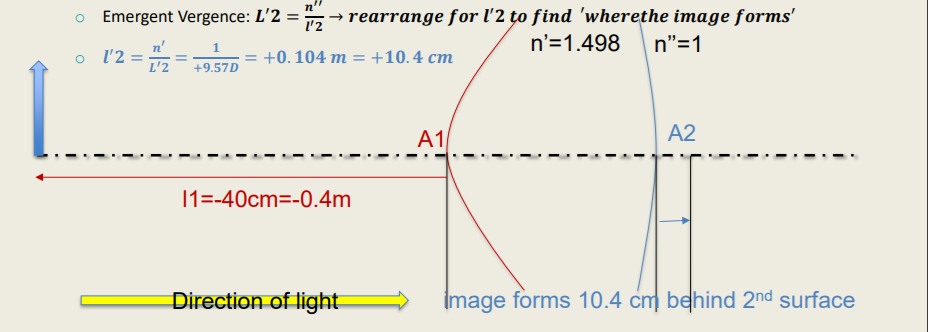
Where will the image form from an object which is placed 40 cm in front of the first surface with a radius of curvature of + 83 mm at a distance of 20 cm away from a second surface with a radius of curvature of -166 mm? the refractive index n between the two surfaces is 1.498

How I calculated this answer:

• Method: Step-Along

• Surface Power: 𝑭 = (𝒏 ′−𝒏) / 𝒓 (given by radius of curvature) and 𝑭 = 𝑳 ′ − 𝑳 → rearrange for L’ (algebra)

  • F1 = (𝒏 ′−𝒏) / 𝒓 = (1.498 - 1) / 0.083m = +6.00D

• Incident Vergence: 𝑳 = 𝒏 / 𝒍 (given by task)

  • L1 = n / i1 → 1 / -0.4m = -2.50D

  • L1’ = F1 + L1 = +6.00D + (-2.50D) = +3.50D

• Emergent Vergence: 𝑳′ = 𝒏′ / 𝒍′ (unknown)

  • L1’ = n’ / i1’

  • i1’ = n’ / L1’ = 1.498 / +3.50D = +0.428 m

  • +0.428 m = 42.8cm

• i2 = i1’ - d = +0.228m

  • L1’ serves as object for surface 2 : 𝒍𝟐 = +𝟎.𝟒𝟐𝟖 𝒎 − (+𝟎.𝟐𝟎 𝒎) = +𝟎.𝟐𝟐𝟖m

• Incident Vergence 2:

  • L2 = n’ / i2 = 1.498 / +0.228 = +6.57D = +6.50D

• Surface power 2:

  • 𝑭𝟐 = (𝒏′ − 𝒏) / 𝒓𝟐 = 𝟏−𝟏.𝟒𝟗𝟖 / −𝟎.𝟏𝟔𝟔𝒎 = +𝟑.00D

  • L2 = F2 + L2 = +3.00D + 6.57D = +9.57D

• Emergent Vergence

  • L2’ = n / i2’ → i2’ = n’ / L2’

  • i2’ = 1 / +9.57D = +0.104m = 10.4cm

• Final answer = 10.4cm

Calculate for yourself and check:

Where will the image form from an object which is placed 40 cm in front of the first surface with a radius of curvature of + 83 mm at a distance of 20 cm away from a second surface with a radius of curvature of -166 mm? Both surfaces are placed in water (n=1.33) and the refractive index n’ between the two surfaces is 1.498

Final answer is 7.52cm. (Come back later to actually work it out as this answer is from chatgpt)

Need to know:

• Refraction is the change in direction of a light wave due to a change in its velocity and the refractive index “n” reflects this relationship.

• Snell’s Law of refraction (plane surfaces): 𝒏 × 𝒔𝒊𝒏 𝒊 = 𝒏′ × 𝒔𝒊𝒏 𝒊′

• Reduced optical thickness: 𝒅 = 𝒕 / 𝒏

• Total internal reflection: 𝐬𝐢𝐧 𝒊_𝒄 = 𝒏_𝒂𝒊𝒓 / 𝒏_{𝒈𝒍𝒂𝒔𝒔} = 𝒏′ / 𝒏

  • Refraction on curved surfaces applying vergence equations:

  • Surface Power: 𝑭 = (𝒏 ′−𝒏) / 𝒓 and 𝑭 = 𝑳 ′ − 𝑳

  • Incident Vergence: 𝑳 = 𝒏 / 𝒍

  • Emergent Vergence: 𝑳′ = 𝒏′ / 𝒍′

  • Parallel rays have a vergence of “0 D”

• One application of the knowledge gained today is BIO – binocular indirect ophthalmoscopy

Refraction is the change in direction of a ____ due to a change in its ____ and the ______ “n” reflects this relationship.

Light Wave; Velocity; Refractive Index