4.7 Bulk Properties of Solids and 4.8 The Young Modulus

Density:

Object low-density materials have a _____ mass and an example:

Mass is measured in ,volume in ____, density will be in ____

Mass is measured in ___ and volume in __ , density will be in _

Density: mass per unit volume of an object

Object low-density materials have a lower mass: Example, balloon less dense than a small bar of lead despite being a larger volume

Mass is measured in g,volume in cm³, density will be in g / cm³

Mass is measured in kg and volume in m³ , density will be in kg/m³

How does a spring stretch and what type of material?

Material obeys hooke’s law if:

Linear relationship of hooke’s law:

What does spring constant measure and if it has a large spring constant mean?

What does hooke’s law apply to?

How is extension and compression determined by?

Extension =

Force is applied to each end of a spring or wire, it stretches, Material with elasticity, e.g. a wire or a bungee rope

Material obeys Hooke’s Law if: The extension of the material is directly proportional to the applied force (load) up to the limit of proportionality

Linear relationship Hooke’s law equation: F = kΔL

Spring constant property of material stretched, measures stiffness of a material, Larger the spring constant, the stiffer the material

Hooke's Law applies to both extensions and compressions:

Extension object determined by its increased in length and Compression of object determined by its decreased in length

extension = stretched length − unstretched length

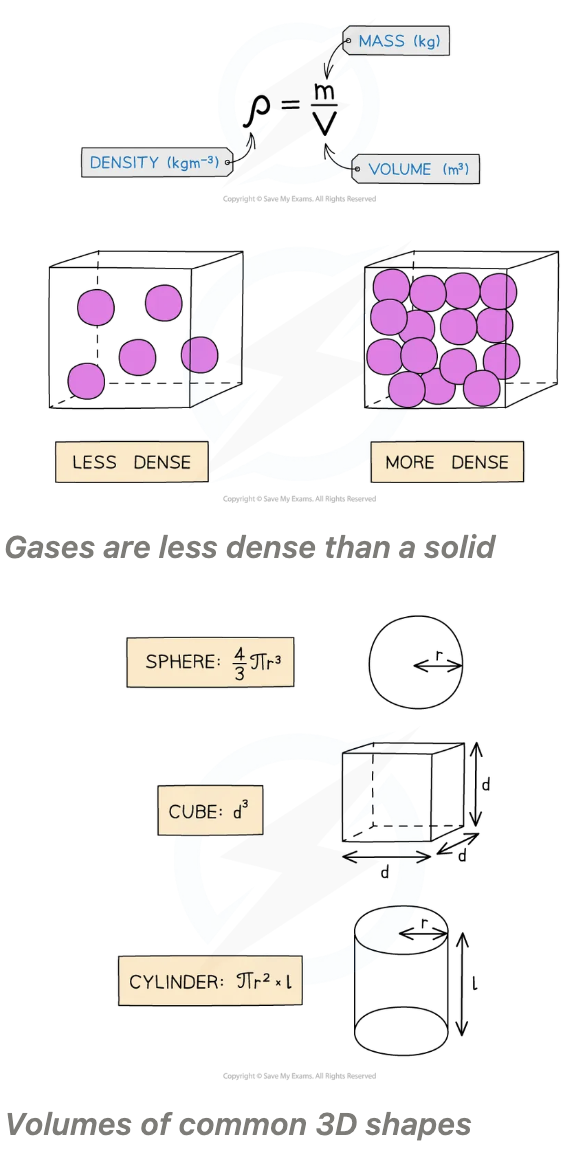
Density:

Object low-density materials have a _____ mass and an example:

Mass is measured in ,volume in ____, density will be in ____

Mass is measured in ___ and volume in __ , density will be in _

Density: mass per unit volume of an object

Object low-density materials have a lower mass: Example, balloon less dense than a small bar of lead despite being a larger volume

Mass is measured in g,volume in cm³, density will be in g / cm³

Mass is measured in kg and volume in m³ , density will be in kg/m³

How does a spring stretch and what type of material?

Material obeys hooke’s law if:

Linear relationship of hooke’s law:

What does spring constant measure and if it has a large spring constant mean?

What does hooke’s law apply to?

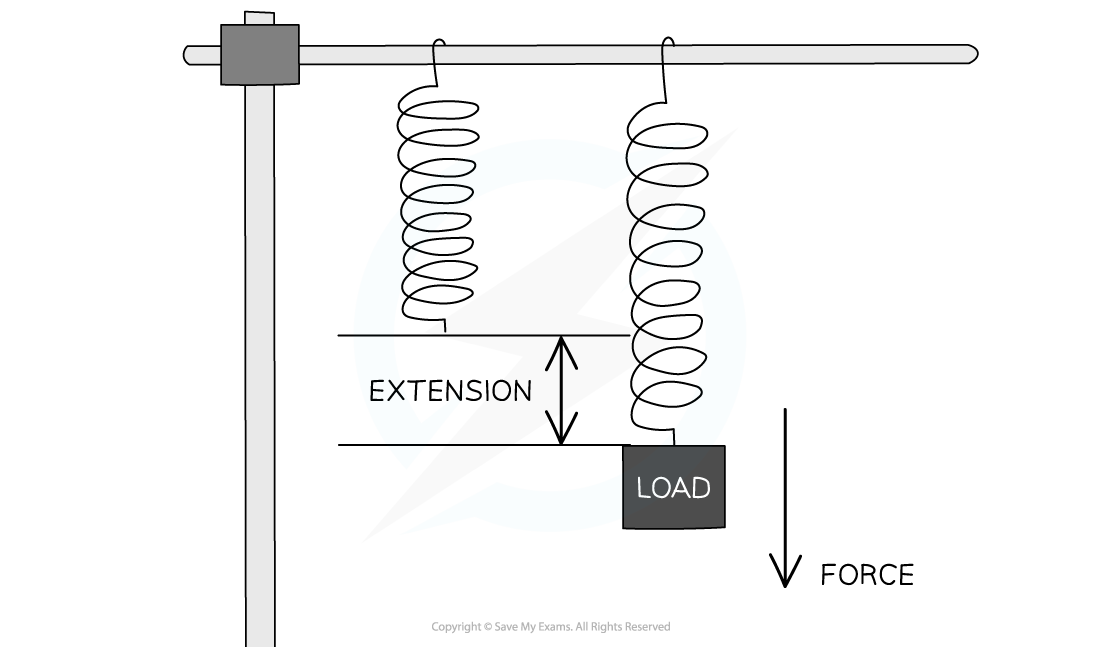
How is extension and compression determined by?

Extension =

Force is applied to each end of a spring or wire, it stretches, Material with elasticity, e.g. a wire or a bungee rope

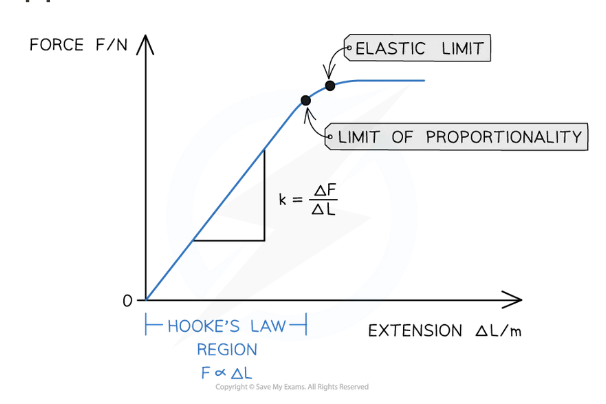
Material obeys Hooke’s Law if: The extension of the material is directly proportional to the applied force (load) up to the limit of proportionality

Linear relationship Hooke’s law equation: F = kΔL

Spring constant property of material stretched, measures stiffness of a material, Larger the spring constant, the stiffer the material

Hooke's Law applies to both extensions and compressions:

Extension object determined by its increased in length and Compression of object determined by its decreased in length

extension = stretched length − unstretched length

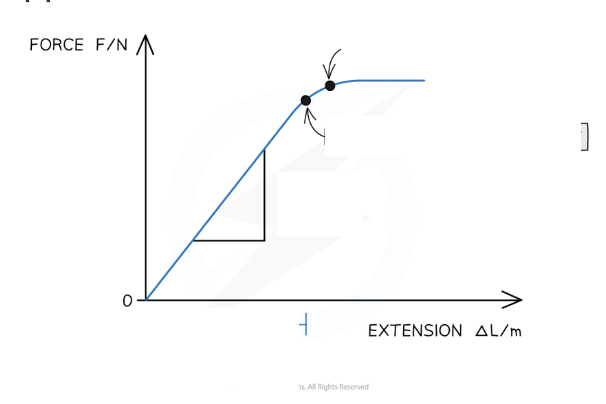
Every material has a ____ force-extension graph depending on how _____ or ______ it is

How is a material that obeys hooke’s law up to a point shown on a force extension graph?

What happens when more force is added/applied?

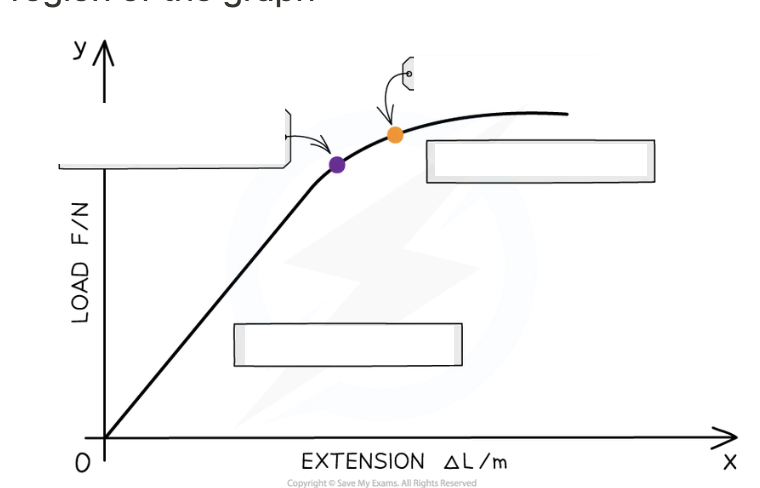
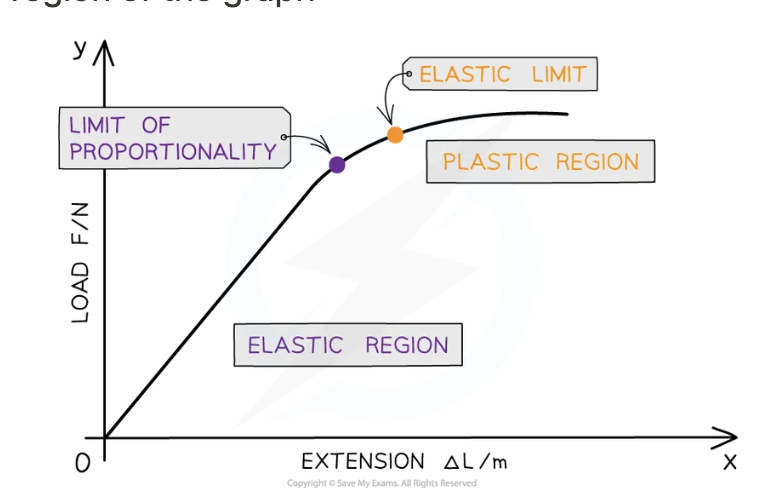
The limit of proportionality:

Elastic limit:

The gradient:

gradient of a force-extension graph -

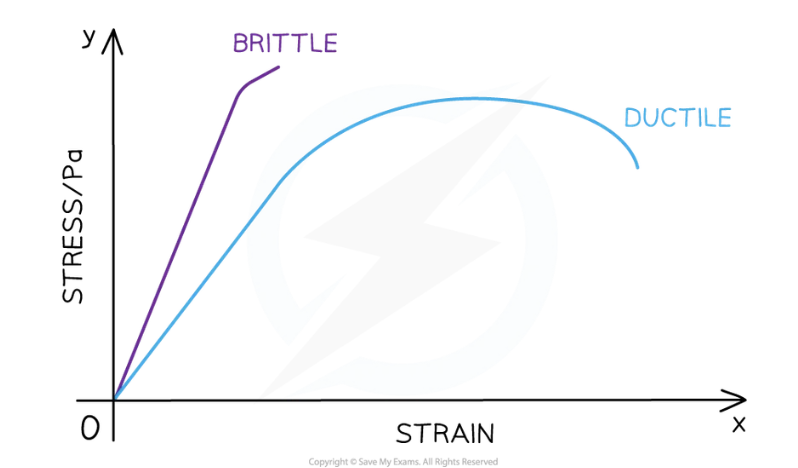
Every material has a unique force-extension graph depending on how brittle or ductile it is

A material may obey Hooke's Law up to a point shown on a force extension graph by a straight line through the origin

More force added, graph starts to curve slightly as Hooke's law no longer applies

The limit of proportionality: Beyond Hooke's law is no longer true , the extension is then no longer proportional to the applied force

Elastic limit: Beyond material no longer return to its original length

The gradient: linear portion of that graph where Hooke's law is obeyed

gradient of a force-extension graph - 1/k = spring constant

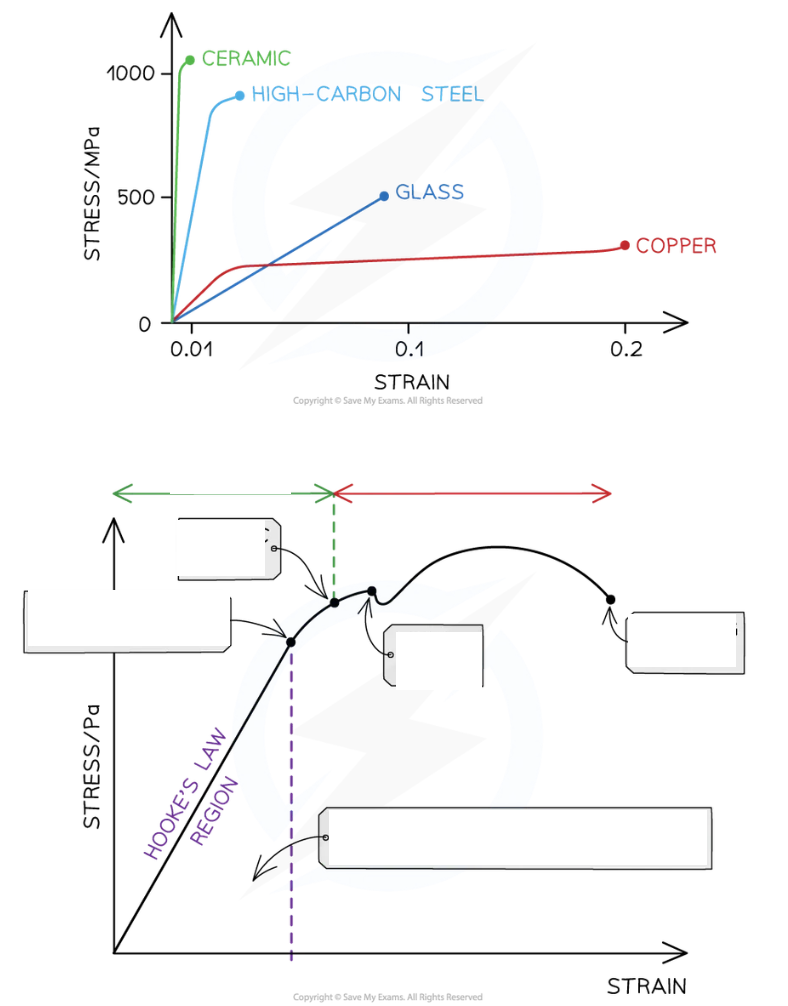
Stress-strain curves describe _____ of materials:

Stress and strain obey Hooke's Law has ____/ ___ behaviour

Material _______ stress-strain curve

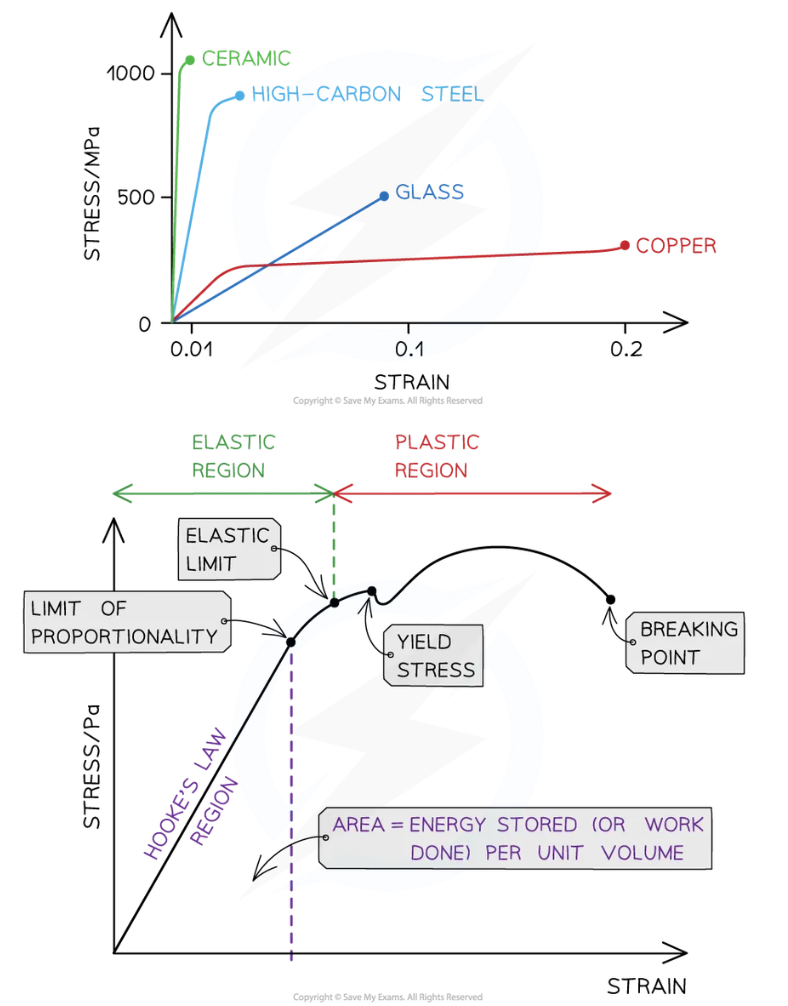
Yield Stress: 

What is the area under the hooke’s law region of the graph?

Breaking point: 

Elastic region:

Plastic region:

Stress-strain curves describe properties of materials: brittle, ductile.

Stress and strain obey Hooke's Law has elastic/ plastic behaviour

Material unique stress-strain curve

Yield Stress: Force per unit area material extends plastically for no/small increase in stress

Elastic strain energy stored per unit volume is the area under the Hooke's Law (straight line) region of graph

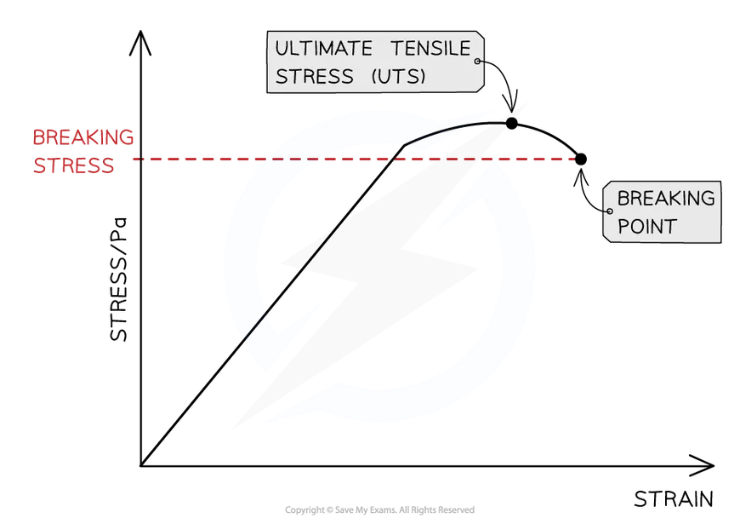
Breaking point: Stress at this point is the breaking stress is the maximum stress a material stand before it fractures

Elastic region: Region of graph up till elastic limit. In the region, material return to original shape when applied force is removed

Plastic region: region of graph after elastic limit. This region, the material deformed permanently, not return to original shape when force applied force is removed

What is done to stretch a material?

Before material reaches ______ ____ obeys Hooke's Law, all _____ is done stored as ______ _____ energy

Area under force-extension graph is

How do you calculate area of graph that does obey hooke’s law?

How do you calculate area of graph that doesn’t obey hooke’s law?

Equation area of right-angled triangle under force-extension graph:

Hooke's Law states F = kΔL, the elastic strain energy:

Before material reaches elastic limit obeys Hooke's Law, all work is done stored as elastic strain energy

Area under force-extension graph is the Work done/elastic strain energy 

For region material obeys Hooke’s law, work done area of  right-angled triangle under the graph

For region where material doesn’t obey Hooke’s law, area is  full region under graph. Calculate area, split the graph into separate segments and add up the individual areas of each

E = ½ FΔL

E = 1/2 k(ΔL)²

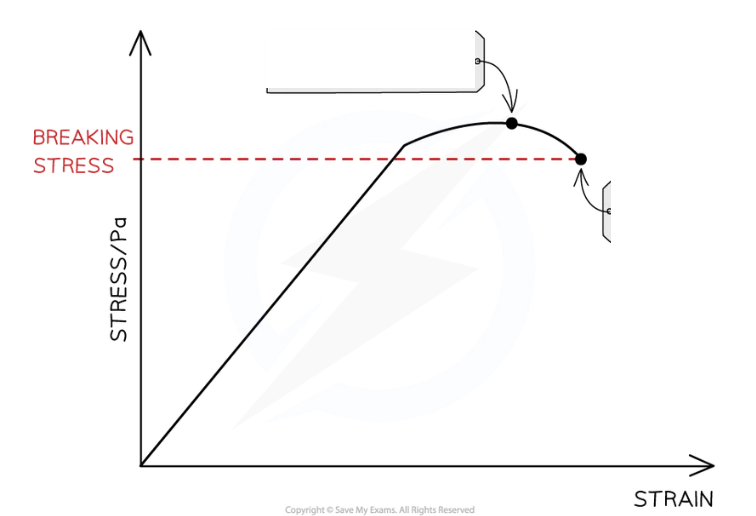
What happens when a greater force is applied on a material?

Breaking stress:

What is a material high breaking stress and what can it do?

Example:

Ultimate tensile stress (UTS) :

UTS and breaking stress depends on condition of material:

Greater force applied on a material so the stress on it increases

Breaking stress: maximum stress a material can stand before it fractures (breaks)

Material high breaking stress is ductile, so it can extend more before breaking due to plastic deformation

Example: copper, good electrical conductor, copper ductile suitable material making wires

Ultimate tensile stress (UTS) is marked on a stress-strain graph: Maximum stress material can withstand

UTS and breaking stress depends on condition of material: its temperature = engineers when considering materials for structure, Material stand extreme temperatures and loads

Vertical spring _____ and _______, energy is ______ into other forms

Total energy of spring remain ______, changing amounts of:

Vertical spring extended and contracted, energy is converted into other forms

Total energy of spring remain constant, changing amounts of:

• Elastic potential energy (EPE)

• Kinetic energy (KE)

• Gravitational potential energy (GPE)

Vertical mass is hanging on spring moves up and down, its energy will convert between the three in various amounts:

At position A:

At position B:

At position C:

Horizontal mass on spring system:

At position A: Spring has some EPE since it is slightly compressed, KE is 0 since it is stationary, GPE is at a maximum because the mass is at its highest point

At position B: Spring has some EPE since it is slightly stretched, KE is at a maximum as it passes through the equilibrium position at its maximum speed, some GPE since the mass is still above the ground

At position C: Spring has its maximum EPE because it is at its maximum extension, KE is 0 since it is stationary, GPE is at a minimum because it is at its lowest point above the Earth's surface

Horizontal mass on spring system, no gravitational potential energy, Spring converts between kinetic and elastic potential energy

Elastic deformation:

Plastic deformation:

Elastic region:

Plastic region:

Regions divided by the ______ ______

Where does the plastic region start and end?

Elastic deformation: load is removed, the object will return to its original shape shown in the elastic region of the graph

Plastic deformation: material is permanently deformed, load is removed, the object will not return to its original shape or length

Elastic region where extension proportional to force applied to the material (straight line)

Plastic region where extension no longer proportional to force applied to the material (graph starts to curve)

Regions divided by the elastic limit

Plastic region starts at elastic limit and ends at point of fracture (material breaks)

Brittle materials:

Ductile materials:

What is brittle material represented by?

What is ductile material represented by?

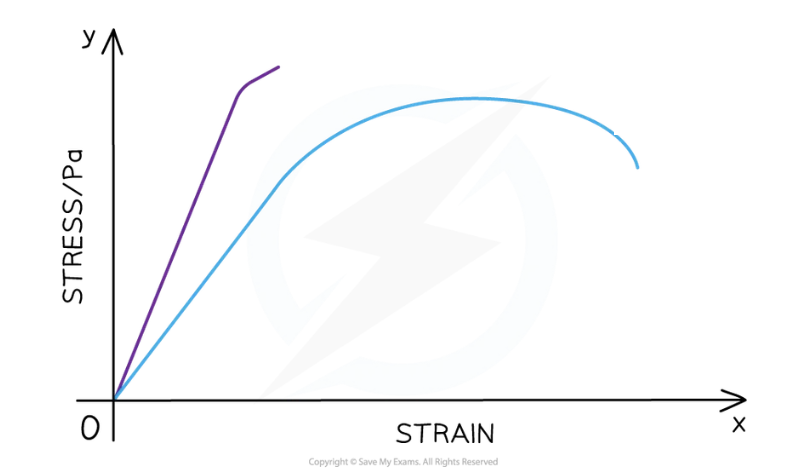
Brittle materials have little/ no plastic region e.g. glass, concrete

• Material breaks with little elastic, insignificant plastic deformation

Ductile materials have larger plastic region e.g. rubber, copper

• Material stretches into a new shape before breaking

Brittle material represented by straight line through origins with no/negligible curved region

Ductile material represented with a straight line through origin then curving towards the x-axis

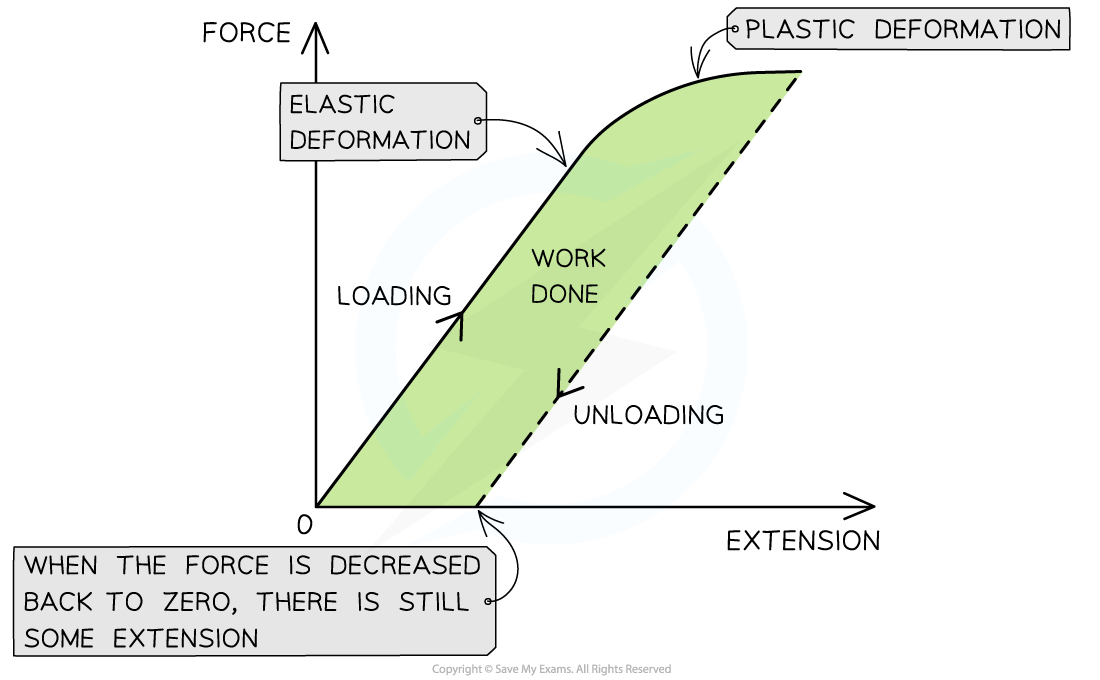
plastic deformation:

What happens when force is removed?

Where is the unloading line on the graph?

What happens to graph when wire is permanently deformed?

What does the area between loading and unloading represent?

plastic deformation: Metal wire loaded with force and stretched beyond limit of proportionality

Force removed, wire unloaded, causing the extension to decrease

Unloading line parallel to loading line (since k does not change) however,  doesn’t go through the origin

Wire permanently deformed, not be at zero extension when there is no force it’s now permanently extended

Area between loading and unloading lines represents work done to permanently deform the wire

Will force-extension graph be the same of loading and unloading?

Rubber band no extension when load fully removed, __ ________ extension so rubber band is _____

Curve for contraction is always _____ the curve for stretching

Key features of the area under the graph are:

Area X work done _______ the rubber (Increase in _______ energy)

Area Y work done by rubber ___________ to its original shape

Area X + Y represents work done _______ rubber band originally

Conservation energy, ________ in strain energy when loading and unloading must be accounted for

Rubber band becomes _______ when stretched and contracted some energy is transferred to _____ energy

Force-extension graph for material not always be the same when loading (adding a force) and unloading (removing a force)

Rubber band no extension when load fully removed, no permanent extension so rubber band is elastic

Curve for contraction is always below the curve for stretching

Key features of the area under the graph are:

Area X work done strectching the rubber (/increase in thermal energy)

Area Y work done by rubber returned to its original shape

Area X + Y represents work done stretching rubber band originally

Conservation energy, difference in strain energy when loading and unloading must be accounted for

Rubber band becomes warm when stretched and contracted some energy is transferred to heat energy

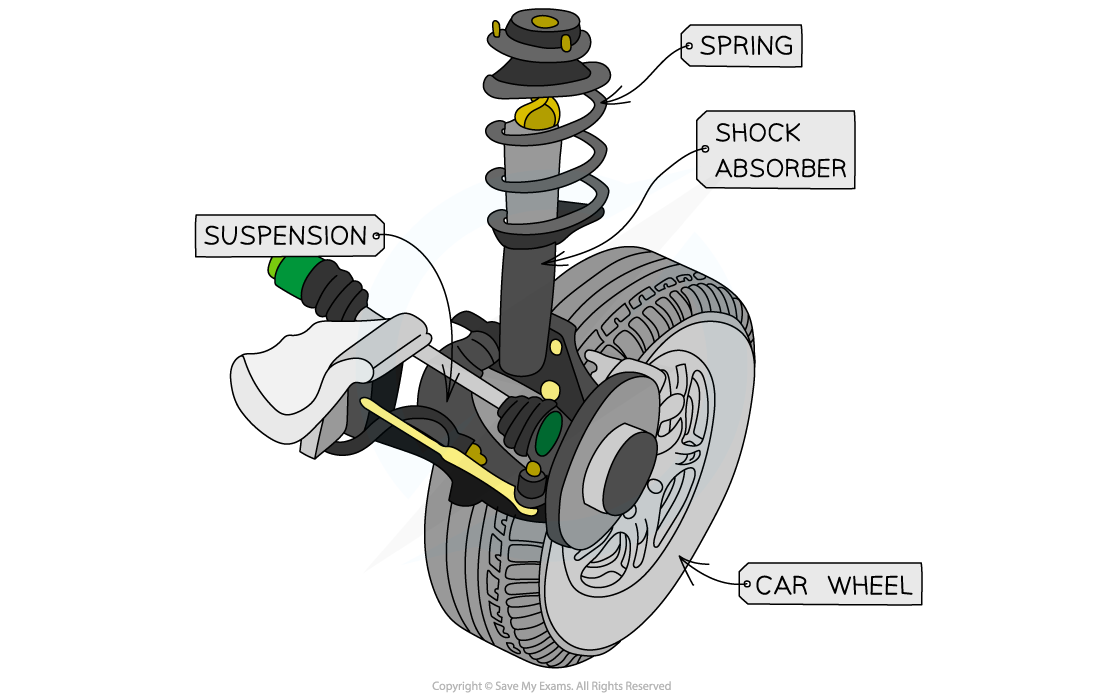
Vehicle suspension systems:  

Why are roads very bumpy and what does this cause the wheel do?

What does this make the wheel do and what could it potentially cuase?

Vehicle suspension systems:  tires, springs and shock absorbers providing comfortable handling of vehicle and improve comfort of passengers

Roads often very bumpy filled with potholes, speed bumps so bump in road causes wheel of vehicle to move up and down perpendicular to the road surface.

Wheel loses contact with road surface, slam back down again causing large vibrations within the car and potentially damage the vehicle

Energy is absorbed by shock absorbers:

What does it help do for tires?

What happens when a vehicle hits a bump in the road?

Faster springs in suspension system move…

Energy is absorbed by shock absorbers: elastic objects designed to absorb or dampen the compression and rebound of the springs above a vehicle’s tire

keep the tires on the road at all times

Vehicle hits a bump in a road, the shock absorbers dampen the movement of the springs in the suspension system by converting kinetic energy, from the movement of the car, into thermal energy which is dissipated

Faster springs in suspension system move (say, if a vehicle hits a bump at a high velocity), more resistance the shock absorber provides

What is young’s modulus and why is it useful for engineers?

What is young modulus defined as and calculations:

Young Modulus of material typically _____ ____ number, in the order of GPa

Young modulus: measure of ability of a material to withstand changes in length with an added load gives information about the stiffness of a material

Useful for engineers to make sure materials using can withstand sufficient forces

Young Modulus is defined as the ratio of tensile stress and tensile strain

young modulus = tensile stress/ tensile strain = Fl / AΔL pascal = strain

Young Modulus of material typically very large number, in the order of GPa

Young Modulus is the ______ of stress-strain graph when it is _____ (a ______ ____) which is the region ____ _______ is _______

Area under graph in this region is the ______ ______ __ _____ ________ of the material

Young Modulus is the gradient of stress-strain graph when it is linear (a straight line) which is the region in which Hooke's Law is obeyed

Area under graph in this region is the energy stored per unit volume of the material