Scientific Notation, Significant Figures, and Measurement Units in Science

Unit

A unit is a standard, agreed on quantity by which other quantities are measured.

Scientific Notation

A method to write large and small numbers more compactly.

Positive Exponent

Means 1 multiplied by 10 n times.

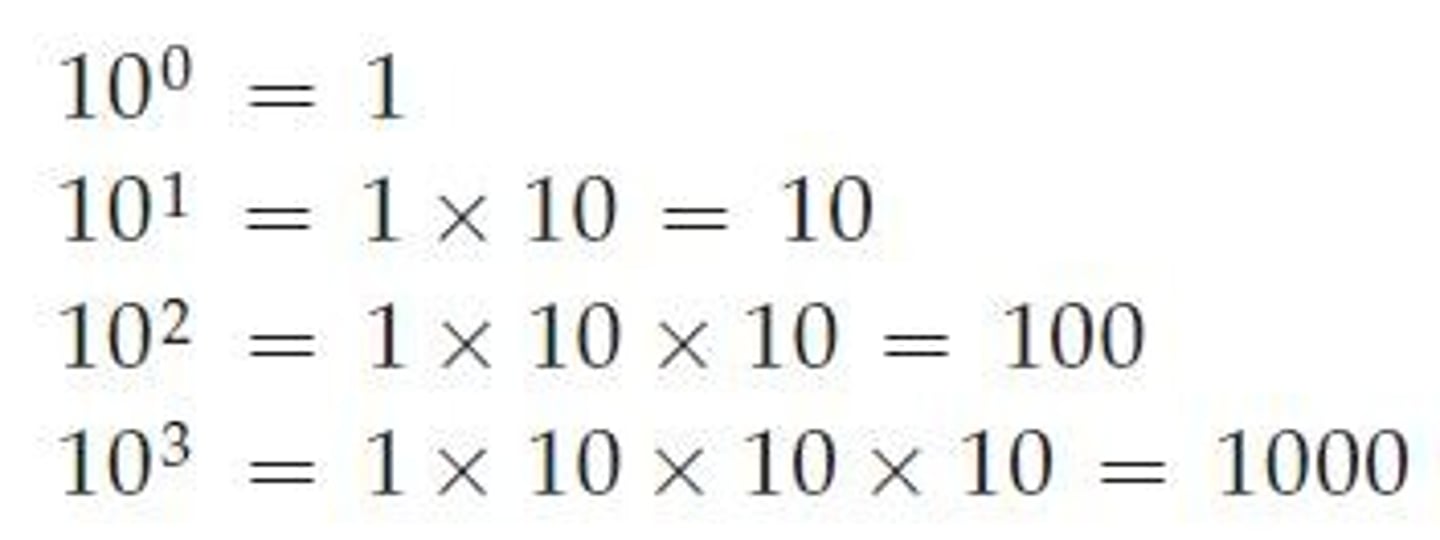
Negative Exponent

Means 1 divided by 10 n times.

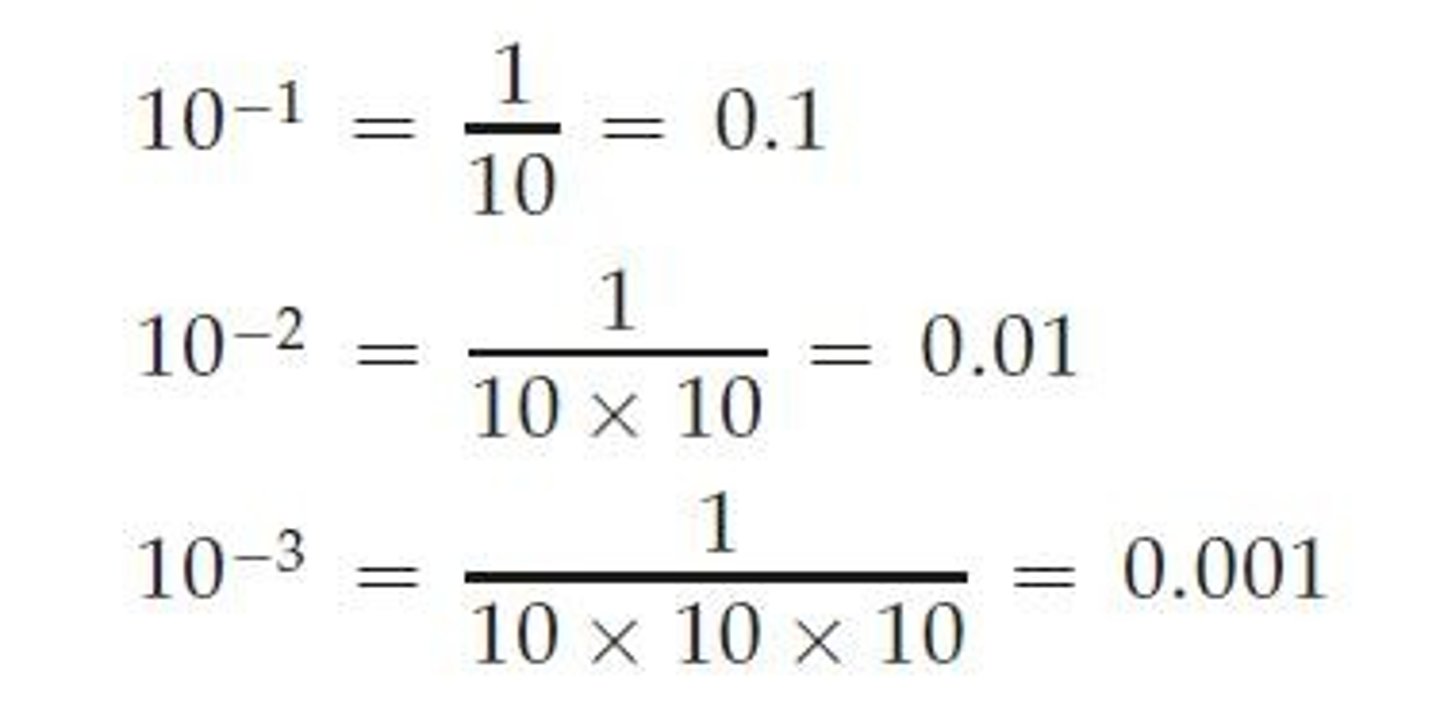
Decimal Part

The part of a number in scientific notation that is between 1 and 10.

Exponential Part

The part of a number in scientific notation that indicates the base (10).

Exponent Part

The part of a number in scientific notation that indicates how many times to multiply or divide by 10.

Population of China in 2017

Approximately 1,387,000,000 people, expressed in scientific notation as 1.387 x 10^9 people.

0.00000867 in Scientific Notation

Expressed as 8.67 x 10^-6.

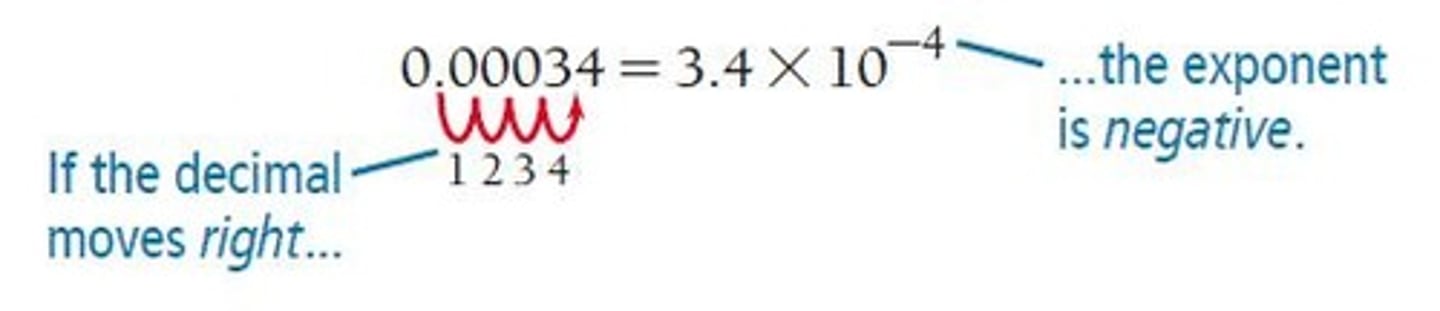
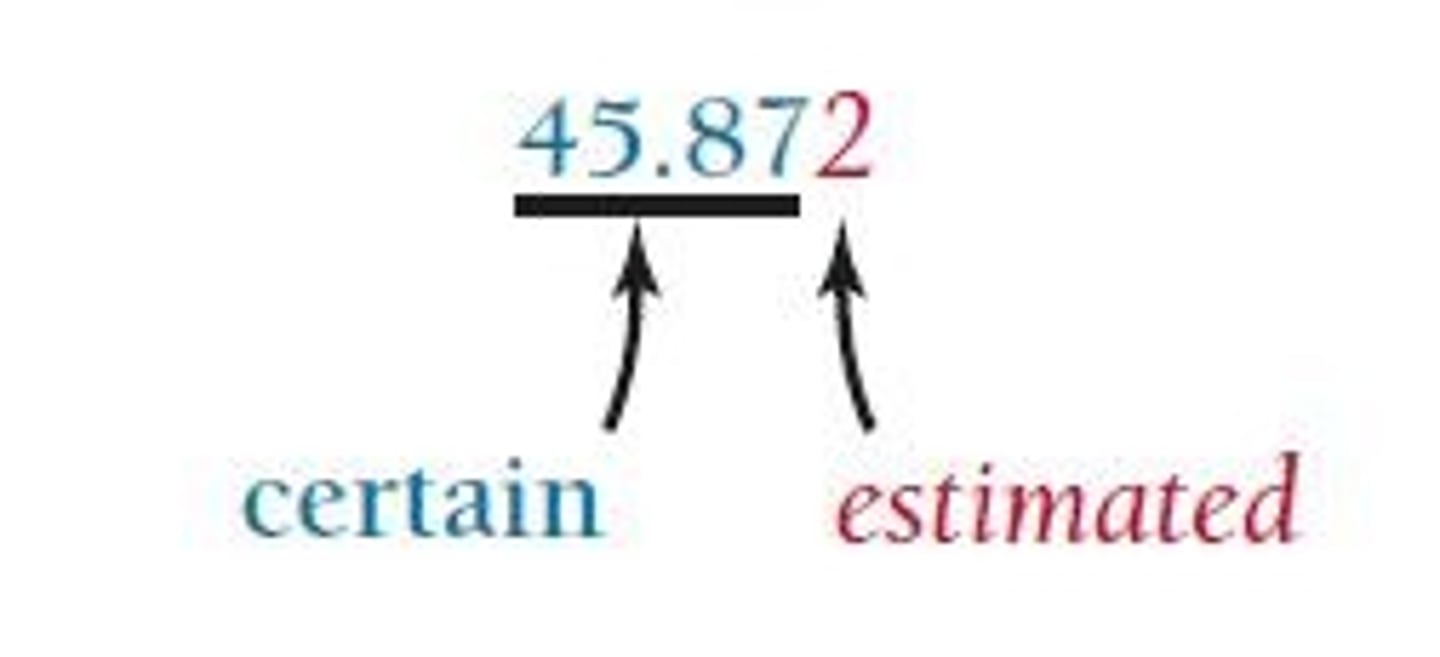
Precision in Measurement

The number of reported digits reflects the precision in the measurement.

Average Global Temperature Increase

Reported as 0.7 °C, meaning 0.7 ± 0.1°C.

Significant Figures

The non-place-holding digits in a measurement that represent the precision of a measured quantity.

Leading Zeros

Do not add to the precision of the measurement.

Trailing Zeros

Add to the precision of the measurement when they follow a decimal point.

Measurement of Copper Sulfate Salt

The correct reading is 1.3 g, estimated from a balance with markings every 1 g.

Measurement of Pistachio Nut

The correct reading is 1.26 g, estimated from a balance with markings every 0.1 g.

Significant Figures in 350

350 = 3.5x10^2 (two significant figures), 350 = 3.50x10^2 (three significant figures).

Uncertainty in Measurement

Indicated by the last reported digit.

Decimal Point Movement

If moved to the left, the exponent is positive; if moved to the right, the exponent is negative.

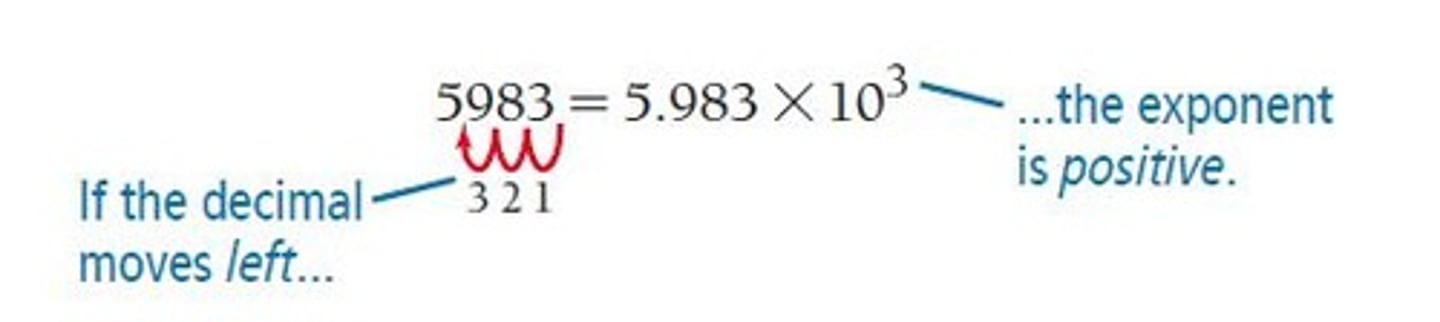
Cumbersome Numbers

Many zeros in large or small numbers make them cumbersome to write.

Example of Temperature Reporting

The temperature rise could be as much as 0.8 °C or as little as 0.6 °C.

Exact Numbers

Numbers that have an unlimited number of significant figures.

Defined Quantities

Quantities that are exact, such as the number of centimeters in a meter.

Ambiguous Significant Figures

Numbers like 2100 that can have different significant figures based on context.

Rounding Rules

Round down if the last digit dropped is 4 or less; round up if it is 5 or more.

Addition and Subtraction Rule

The quantity with the fewest decimal places determines the number of decimal places in the answer.

Multiplication and Division Rule

The quantity with the fewest significant figures determines the number of significant figures in the answer.

SI Units

The International System of Units used for scientific measurements.

Mass

A measure of the quantity of matter within an object.

Weight

A measure of the gravitational pull on an object, calculated as W = mg.

Kilogram

The base unit of mass in the SI system, defined as 1000 grams.

Gram

A common unit of mass defined as 1/1000 of a kilogram.

Decimal Point Significance

A decimal point indicates that trailing zeros are significant.

Significant Figures in Scientific Notation

The number of significant figures can change based on how the number is expressed in scientific notation.

Calculations with Significant Figures

In calculations involving both multiplication/division and addition/subtraction, complete steps in parentheses first.

Example of Rounding

To round 2.349 to two significant figures, it becomes 2.3.

Example of Addition

3 + (1.25) = 4.25 rounds to 4 (one significant figure).

Example of Division

18/12 = 1.5 (two significant figures).

Significant Figures in 2100

2100 can be ambiguous without a decimal point; with a decimal, it has 4 significant figures.

Measurement Systems

The two most common systems are the English system and the Metric system.

Integral Numbers in Equations

Integral numbers that are part of an equation are considered to have an unlimited number of significant figures.

Example of Significant Figures

58.31 has 4 significant figures.

SI Prefix Multipliers

They change the value of the unit by powers of 10.

1 km

1000 m = 10^3 m

1 ms

0.001 s = 10^-3 s

Derived units

A derived unit is formed from other units.

Volume

Any unit of length raised to the third power.

Density

Mass per unit volume.

Speed

Distance covered per unit time.

Dimensional analysis

Using units as a guide to solving problems.

Conversion factor

A quotient with the desired unit on top and the given unit on the bottom.

1 in.

2.54 cm

1 ft

12 in.

Velocity of a car

65 km/hr = 18 m/s

Cubic centimeters (cm3)

When converting, raise the conversion factor to that power.

Density of a substance

The ratio of its mass to its volume.

Units for density

g/cm3 or g/mL

Density of water

1 g/mL

Density of mercury

13.6 g/mL

Density of the Dead Sea

1.24 g/mL

Density of sea water

1.03 g/mL

Density calculation example

Density = 9.67 g / 0.452 cm3 = 21.393 g/cm3

Volume measurement example

To measure 68.4 g of a liquid with a density of 1.32 g/cm3, measure 0.052 cm3.

Mass (m)

35 mg

Density (d)

0.788 g/cm3

Solution Map for density

mg -> g -> cm3

1000 cm3

1 L

Density of Platinum

21.4 g/cm3