Hoofdstuk 1: introductie - modsim

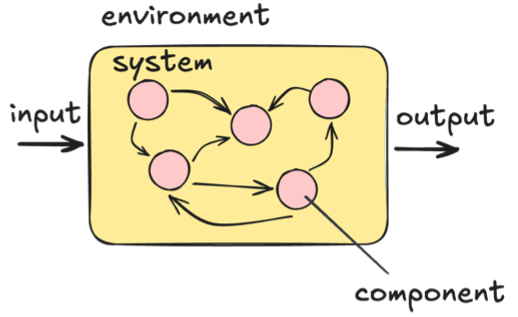
system

a set of elements, parts, or components coherently organized and interconnected into a pattern or structure that produces a characteristic set of behaviors called a function or purpose

function: natural systems

purpose: man-made systems

natural system

vb ecosystem or solar system

manufactured or artificial system

vb company, railway system

closed system

no exchange with environment

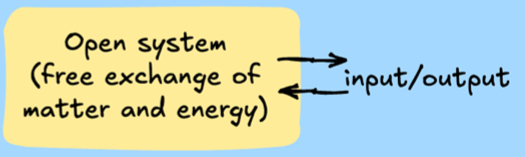
open system

free exchange of matter and energy

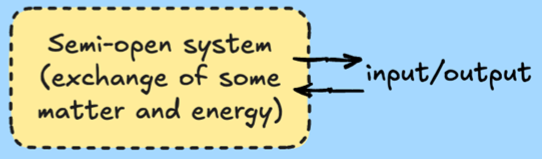
semi-open system

exchange of some matter and energy

stocks and states

elements that can be quantified at a given time, but they differ in scope

elements that are quantified at a different time. In a diagram they are represented by boxes in diagrams

stocks

accumulated quantity of a specific resource or material, both tangible and intagible

are accumulated and act as buffers

states

encompass a broader range of conditions or situations, includig physical variables and even more abstract concepts

more general and involve both physical variables

inputs

enter the system

outputs

leave the system

flows

represent the moments of resources into, out or within a system. they are drawn as arrows, can be positive or negative and change the stock by filling, draining, growing, producing, decaying, evalorating, losing, secreting, or transforming it.

∆stock =

ingoing flows - outgoing flows

engineer a stock

by manipulating the in-or outgoing flows

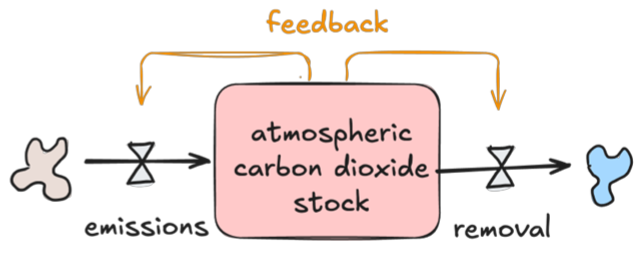
feedback

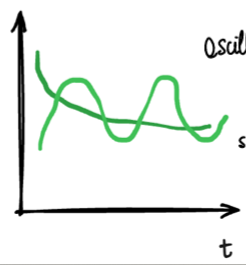
a closed chain of causal connections where a change in a stock affects a flow, which in turn affects the stock again. It's the mechanism by which a system can regulate itself, either by amplifying or dampening change.

positive feedback

the higer the value of the stock, the faster it increases, often destabilizing

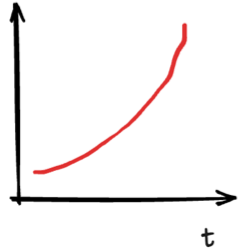
negative feedback

opposes the original change, inhibits its own activity, usually a stabilizing force

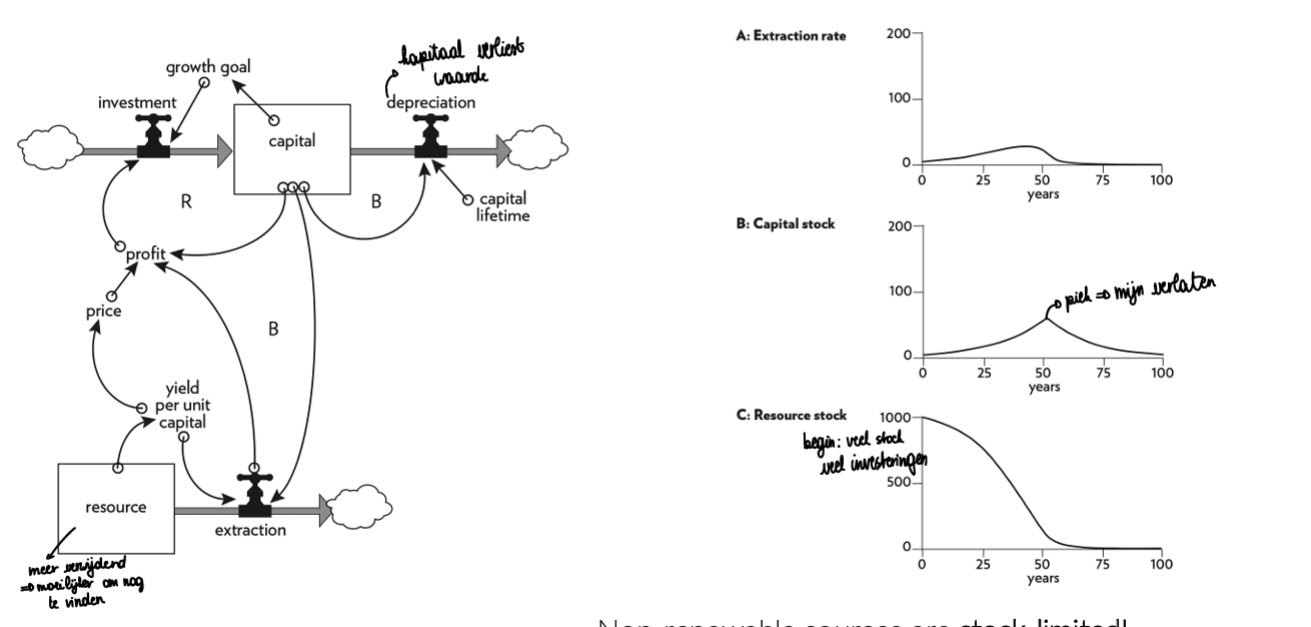
non-renewable stock

stock-limited

positive feedback: more profit → invest more

negative feedback: more stock removed → harder to extract remaining oil

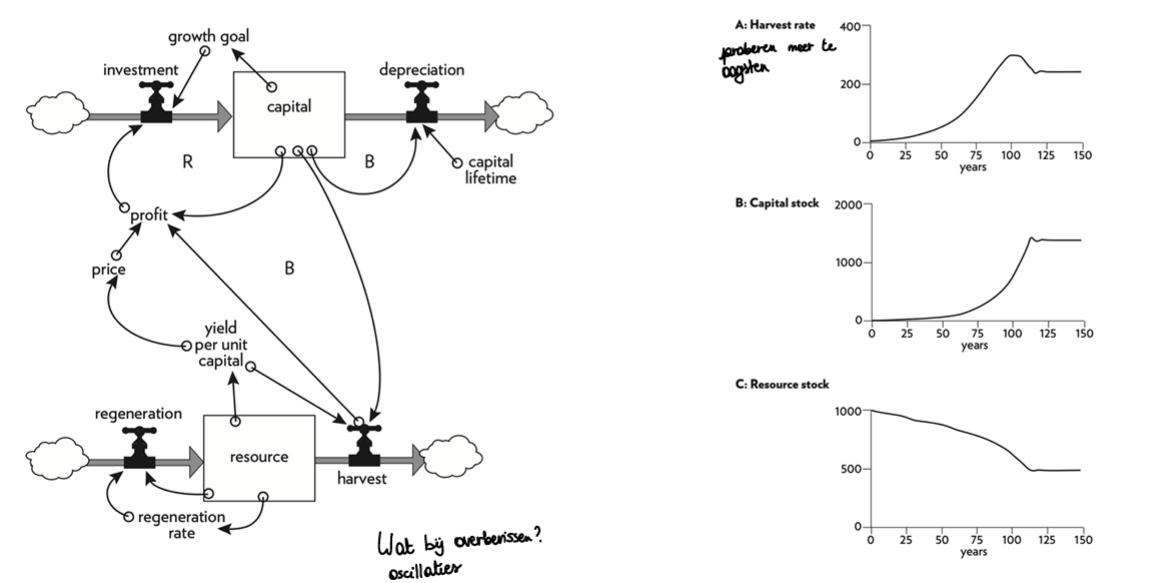
renewable stock

flow-limited

mathematical model

a simplified representation of a real-world system or phenomenon using mathematical equations, relationships, and logic to understand, predict, or control its behavior:

• They relate to a specific system

• They are a simplification (abstraction, idealization)

• They must be quantitative

physical or conceptual models

key aspects of a mathematical model

• states or variables

  • indepent variables

  • dependent variables

• constants

• parameters

states or variables

dexcribe the system at a given time (= stocks)

independent variables

known and set (time, spatial coordinates, fixed inputs…)

dependent variables

change depending on the other model components (vb pressure or concentration)

constants

quantities that are known and fixed (mathematical and physical constants)

parameters

values that can change from experiment to experiment, usually need to be determined experimentally

! fixed within a particular run in a model (otherwise variables)

inputs (model, control theory)

often independent variables, one can control

outputs (model, control theory)

the states one can observe

complex vs simple models

More complex models can

• Be more realistic and perform more specific predictions

• Can represent more detailed information about the system

However, compared to simple models, they

• Require more data to calibrate and validate

• Are more difficult to understand

• Are computationally more costly.

trade-off between accuracy, interpretability and computational resources

reasons for creating mathematical models

1. for forecasting and the prediction of future states;

2. for the design and optimization of the system;

3. for estimation and control, using feedback and measurements;

4. for interpretability and physical understanding.

linear model

a change in the input corresponds to a proportional change in the output

• usually easy to work with, understand and solve

• Taylor approximation to create locally linear approximations of nonlinear models

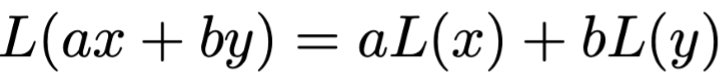
nonlinear model

change in one variable does not lead to a proportional change in another

• challenging or even impossible to solve analytically

static model

describes system at a fixed point in time

dynamic model

capture how systems change and evolve over time

can be studied in a steady state

discrete models

• Represent systems as a collection of distinct, separate elements or states.

• Variables change in defined steps or jumps.

• Examples: Board games, queuing systems, population models with discrete generations.

continuous models

• Represent systems with smooth, unbroken changes.

• Variables can take on any value within a range

• Examples: Fluid flow, temperature changes, motion of planets.

computer

discreet apparaat, maar eigenlijk is alles continu

discrete or continuous

• State variables: Discrete (e.g., number of customers) vs. continuous (e.g., temperature).

• Space: Discrete (e.g., grid cells) vs. continuous (e.g., any point in a region).

• Time: Discrete (e.g., time steps) vs. continuous (e.g., any point in time).

explicit models

output or future state of the system is calculated directly from the current state and the known inputs

formule voor y(x) bestaat, niet als dv

implicit model

output or future state is not directly calculated. It’s implicitly defined through an equation involving both the current and future states. This equation needs to be solved to find the future state

chaotic model that will show dynamics strongly dependent on the initial conditions and parameters

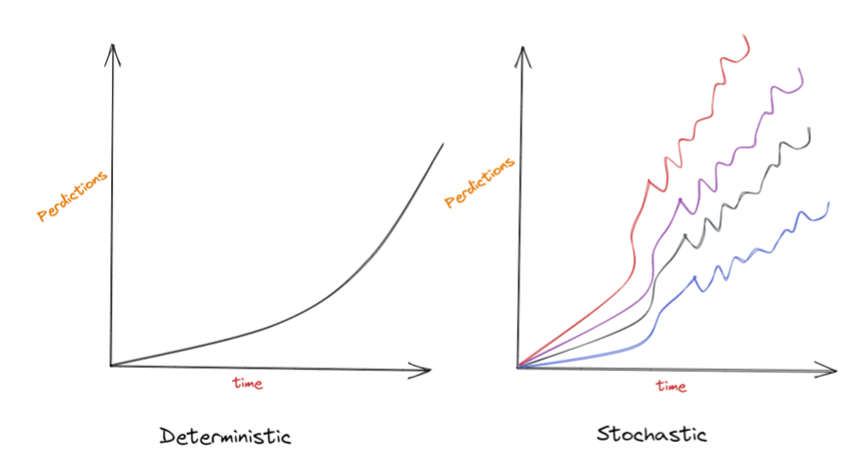
deterministic models

• Outcome is fully determined by the initial conditions and the model's equations.

• No randomness involved; the same inputs always produce the same outputs.

• Example: Predicting the trajectory of a projectile in a vacuum.

stochastic models

• Incorporate randomness or probability in their calculations.

• Same inputs can lead to different outputs due to inherent uncertainty.

• Example: Predicting the spread of a disease, where individual interactions are unpredictable.

all computers are

deterministic, randomness is artificial

Probabilistic ≠ stochastic

• Probabilistics involves probability distributions; computations can be perfectly deterministic.

• Stochastic models use randomness in their computation.

data-driven model

mainly guided by observed data

+ Capture any pattern given enough data

+ Good for prediction

- Might not generalize

- Lower explanatory power

mechanistic model

mainly based on the knowledge of underlying processes and physical laws

+ Can generalize to new scenarios

+ Insight into underlying processes

- Required detailed knowledge

- Sometimes computationally expensive

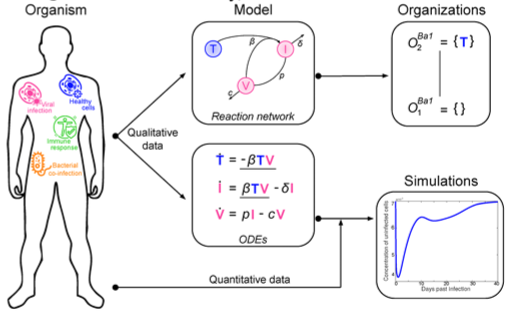
in practice

always overlap between data-driven and mechanistic model

data-driven modelling

compressing data into a model or statistic

simulation-bades modelling

compressing data into a model or statistic

model opgesteld o.b.v. kennis → data genereren

spatially explicit

• Considers the location and spatial arrangement of components.

• Captures interactions and processes that depend on location.

• Example: Spread of a disease in a city, considering how people move and interact.

spatially implicit

• Ignores spatial locations and assumes all components are "well-mixed.”

• Simpler but may not capture important spatial dynamics.

• Example: Basic population growth model without considering where individuals live.

distributed models

• Consider spatial variation in parameters and variables.

• Represent the system as a collection of interconnected components or elements.

• More realistic for systems with significant spatial heterogeneity.

• Example: Modelling temperature distribution in a rod, considering heat transfer along its length.

lumped models

• Treat the system as a single, homogeneous unit.

• Ignore spatial variations and assume uniform properties throughout.

• Simpler to analyze but may lose accuracy in spatially complex systems.

• Example: Modelling the average temperature of a room, assuming uniform temperature distribution.

simulation

the imitation of the operation of a realworld process or system over time. It involves creating a simplified representation (i.e., the model) of the system and using it to study its behavior under different conditions or scenarios

virtual experimenting

simulation on a computer

• cheaper

• faster

• safer

than real-world experiments

digital twin

a simulation model of a real system that has a bidirectional flow of information:

• The digital twin is updated in real-time using sensor measurements of the physical twin

• The digital twin has a predictive capacity to inform decision-making in the physical system.

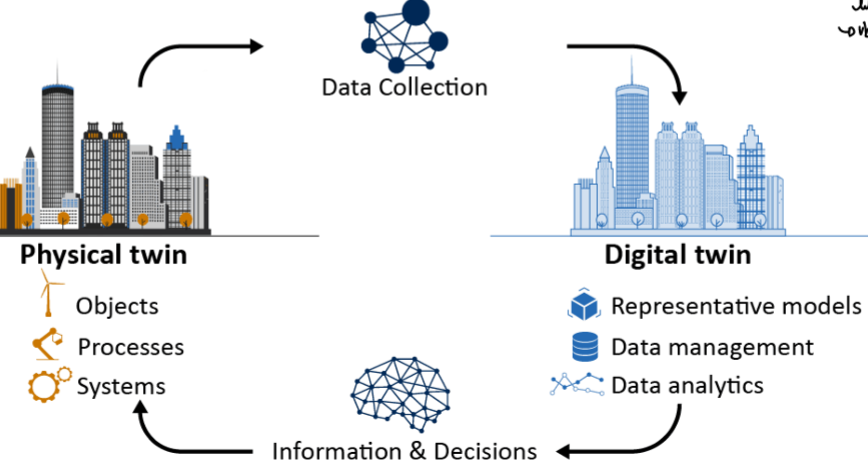
simulation cycle

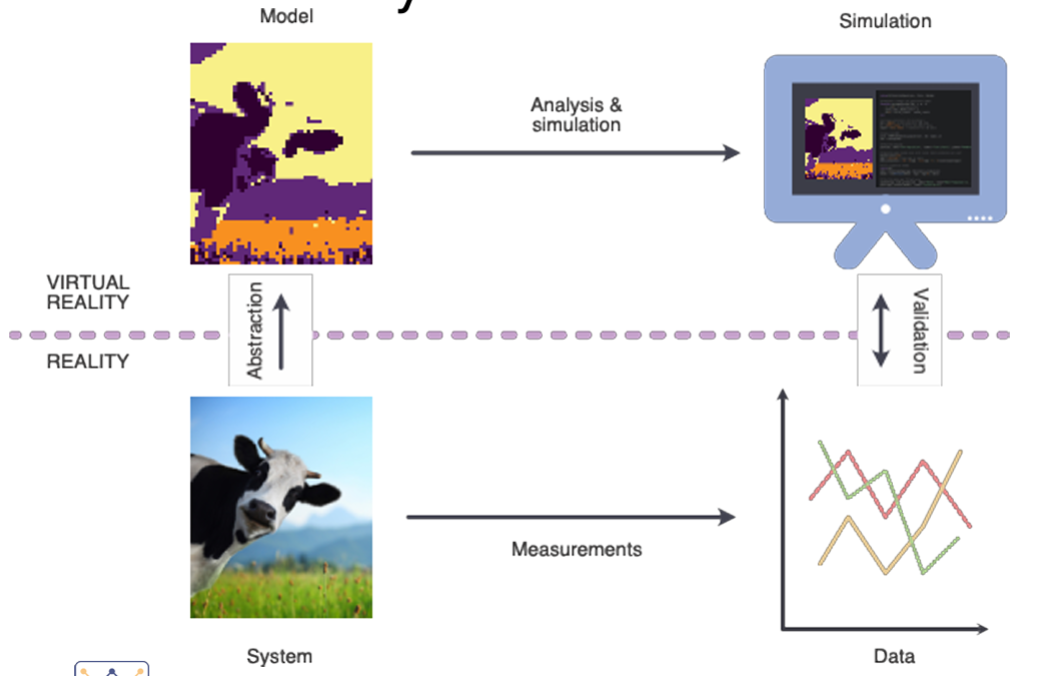
the Simulation Hypothesis

the belief that we live in a simulation, arguments:

1. Future civilizations might possess the immense computing power needed to create ancestor simulations.

2. Such civilizations might have reasons to run numerous ancestor simulations, perhaps for research, entertainment, or other purposes.

3. If many ancestor simulations exist, we are more likely to live in one rather than the “real” world.