Unit 2 Calculus 2

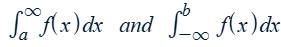
Improper integrals defined by limits

• Convergent - The limit exists. The function goes to zero fast enough for the area under the curve to be finite.

• Divergent - The limit does not exist (unbounded behavior: ±∞ or n/0). The function either goes to zero too slowly or not at all, so the area under the curve is infinite.

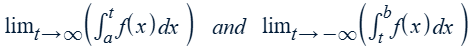
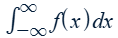
Decompose by splitting the interval

• If both converge, then the original converges.

• If one or both diverge, then the original diverges.

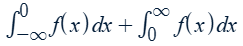
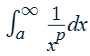
The exponents p for which the improper integral converges or diverges

p > 1: convergent

p ≤ 1: divergent

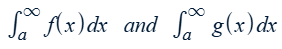
Comparison test for improper integrals

• Conditions: f(x) ≥ g(x) ≥ 0 for x ≥ a

  • f(x) - a chosen function (often 1/x^p) with known or easily-determinable convergence

    • Tip: f(x) should be similar to g(x) and include g(x)’s highest power

  • g(x) - the given function with unknown convergence

• If f(x) converges or diverges, then g(x) does the same.

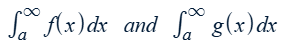
Limit comparison test for improper integrals

• Conditions: f(x), g(x) > 0 for x ≥ a

• If limit > 0, then f(x) and g(x) either both converge or both diverge.

x = k, y = k, and z = k traces

Vertical plane: x = k, y = k

Horizontal plane: z = k

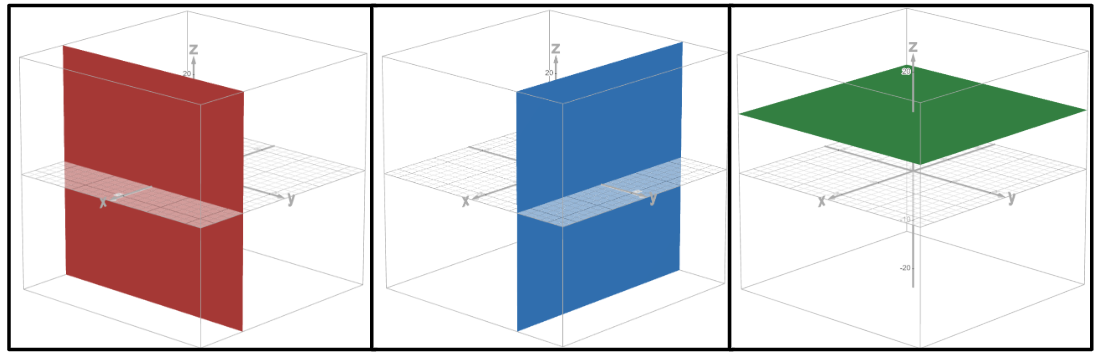
What does it mean when an x, y, or z is missing from an equation?

That variable has no value restrictions, so the graphed function extends across that entire axis.

1. Distance between the points

   P₁(x₁,y₁,(z₁)) and P₂(x₂,y₂,(z₂))

2. Length/magnitude of a 2-D (3-D) vector

   a = <a₁,a₂,(a₃)>

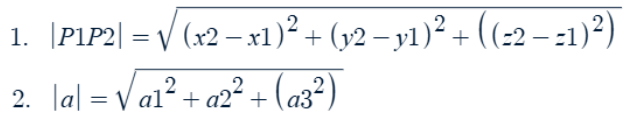
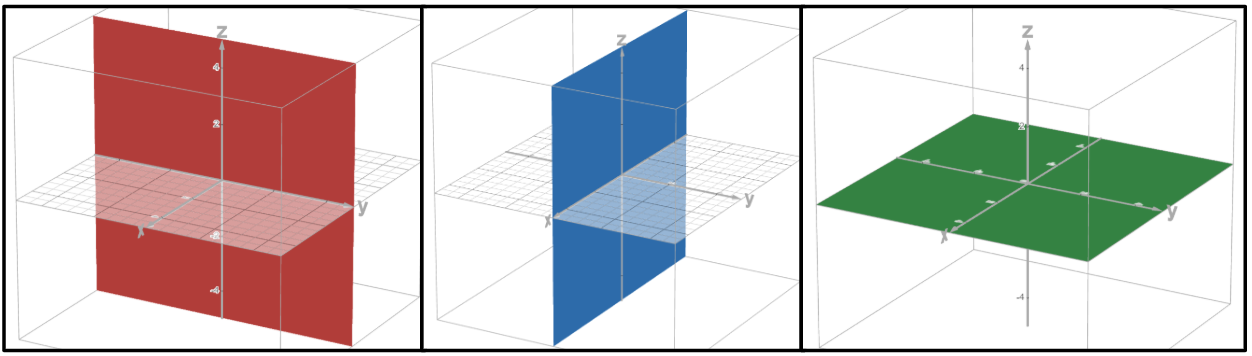
Equation of a sphere

(x – h)² + (y – k)² + (z – l)² = r²

• center point (h,k,l)

• radius r

• Add constants to create trinomials that factor into square binomials:

  • x² + 2ax + a² = (x + a)²

  • x² – 2ax + a² = (x – a)²

  • a² = (2a/2)²

Components of a 2-D (3-D) vector between the points (x₁,y₁,(z₁)) (the tail) and (x₂,y_2,(z₂)) (the arrow head)

<x₂ – x₁, y₂ – y_1, (z₂ – z₁)>

* tells magnitude and direction, NOT position

Addition/subtraction of two 2-D (3-D) vectors:

1. a + b = <a₁,a₂,(a₃)> + <b₁,b₂,(b₃)>

2. a – b = <a₁,a₂,(a₃)> – <b₁,b₂,(b₃)>

1. <a₁ + b₁, a₂ + b₂, (a₃ + b₃)>

2. <a₁ – b₁, a₂ – b₂, (a₃ – b₃)>

Multiplication of a scalar c to a 2-D (3-D) vector a:

ca = c<a₁,a₂,(a₃)>

<ca₁,ca₂,(ca₃)>

* Vector ca has a different length than a and (if c is negative) points in the opposite direction.

Vectors a and b are parallel (a||b) if…

b = ca for some scalar c

OR

a x b = 0

Standard basis vectors in two (three) dimensions

i = <1,0,(0)>

j = <0,1,(0)>

(k = <0,0,1>)

2-D (3-D) vector a = <a₁,a₂,(a₃)> in terms of i, j, and k

<a₁ + 0, a₂ + 0, (a₃ + 0)>

<a₁,0,0> + <0,a₂,0> + (<0,0,a₃>)

a₁<1,0,0> + a₂<0,1,0> + (a₃<0,0,1>)

a₁i + a₂j + (a₃k)

Unit vector â in the direction of a

* 1/|a| is a scalar that makes the length 1

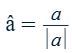
Dot product of two 2-D (3-D) vectors:

a • b = <a₁,a₂,(a₃)> • <b₁,b₂,(b₃)>

a₁b₁ + a₂b₂ + (a₃b₃)

* a number

a • a

<a₁,a₂,(a₃)> • <a₁,a₂,(a₃)>

a₁a₁ + a₂a₂ + (a₃a₃)

a₁² + a₂² + (a₃²)

|a|²

a • b

|a||b|cosθ ← angle between a and b

Vectors a and b are orthogonal/perpendicular (a⊥b) if…

a • b = |a||b|cos(π/2) ← θ = π/2 (90^o)

a • b = |a||b|(0)

a • b = 0

Component of b along a (comp_ab)

aka scalar projection of b onto a

* a number

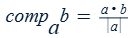
Vector projection of b onto a (proj_ab)

proj_ab = (comp_ab)â

* a•b/|a|² is a scalar

* a vector

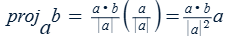
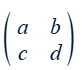
Determinant of a 2×2 matrix

ad – bc

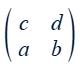
What happens if the rows are flipped?

bc – ad = –(ad – bc)

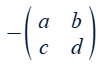
Cross product of two 3-D vectors:

a x b = <a₁,a₂,a₃> x <b₁,b₂,b₃>

a vector

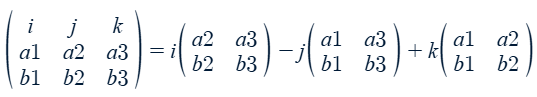
Cross product properties

• a x a = <0,0,0>

• b x a = –(a x b)

  • because the rows are flipped in the 2×2 matrices

• (a x b)⊥a,b

  • Proof of orthogonality: (a x b) • a (or b) = 0

|a x b|

|a||b|sinθ ← angle between a and b

Areas determined by vectors a and b

Parallelogram: A = |a x b|

Triangle: A = ½ |a x b|

*a and b can be any two adjacent sides

Equations for a line with a known 2-D (3-D) point, (x₀,y₀,(z₀)), and a 2-D (3-D) parallel direction vector, v = <a,b,(c)>

Vector: <x,y,(z)> = <x₀,y₀,(z₀)> + t<a,b,(c)> OR <ta,tb,tc>

• t is a scalar called the parameter

Parametric:

• x = x₀ + at

• y = y₀ + bt

• (z = z₀ + ct)

* Another point on the line is needed to find v.

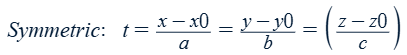
Plane intersection points

yz-plane: x = 0

xz-plane: y = 0

xy-plane: z = 0

Equations for a plane with a known 2-D (3-D) point, (x₀,y₀,(z₀)), and a 2-D (3-D) orthogonal normal vector, n = <a,b,(c)>

Vector: <a,b,(c)> • (<x,y,(z)> − <x₀,y₀,(z₀)>) = 0

<a,b,(c)> • <x − x₀, y − y₀, (z − z₀)> = 0

Scalar: a(x − x₀) + b(y − y₀) + (c(z − z₀)) = 0

ax − ax₀ + by − by₀ + (cz − cz₀) = 0

Linear: ax + by + cz = ax₀ + by₀ + cz₀

Relationship between the normal vector (n) and two parallel vectors (a and b) of a plane (S)

If n⊥S and a,b||S, then n⊥a,b:

n = a x b

* a and b can be found from 1.) the direction vector of a line on the plane or 2.) between points on the plane

Axes intersections

x-intercept: y,z = 0

y-intercept: x,z = 0

z-intercept: x,y = 0

Angle of intersection between planes S and T

It is the same as the angle θ between their normal vectors:

n_S • n_{T =} |n_S||n_T|cosθ

OR

|n_S x n_T| = |n_S||n_T|sinθ

Relationship between the normal vectors (n_S and n_T) of two planes (S and T) and the direction vector (v) of their intersection line

If v||S,T, n_S⊥S, and n_T⊥T, then v⊥n_S,n_T:

v = n_S x n_T

* A point on both S and T is needed to find the intersection line equation. One way is to let one variable be zero and then find the others using a system of S and T’s linear equations.

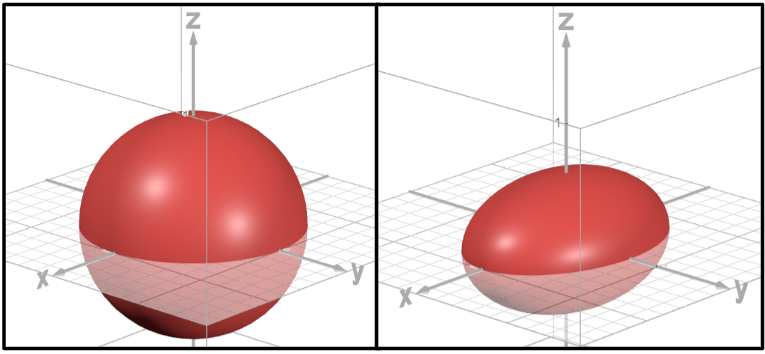
Ellipsoid

• All traces are ellipses.

• spherical if a = b = c

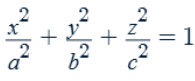
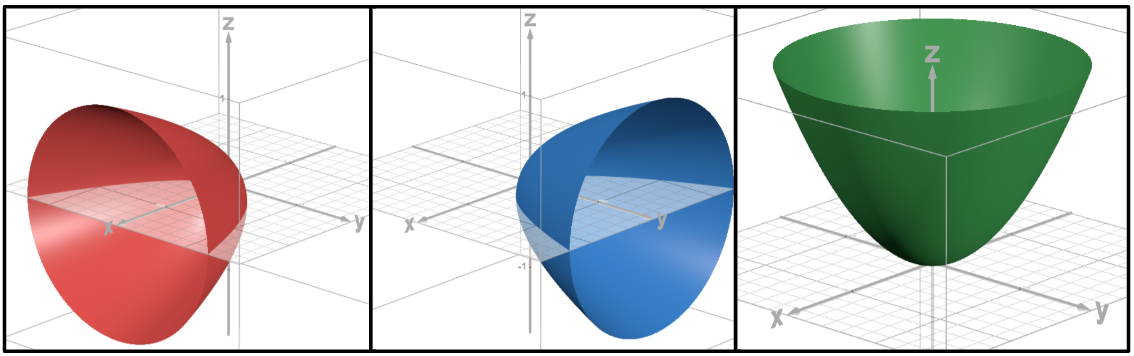
Elliptic paraboloid

• The variable with a power of 1 is the axis of symmetry.

• Traces along the axis of symmetry are ellipses. Traces along the other two axes are parabolas.

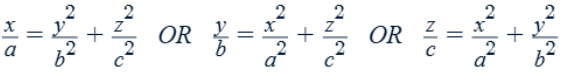
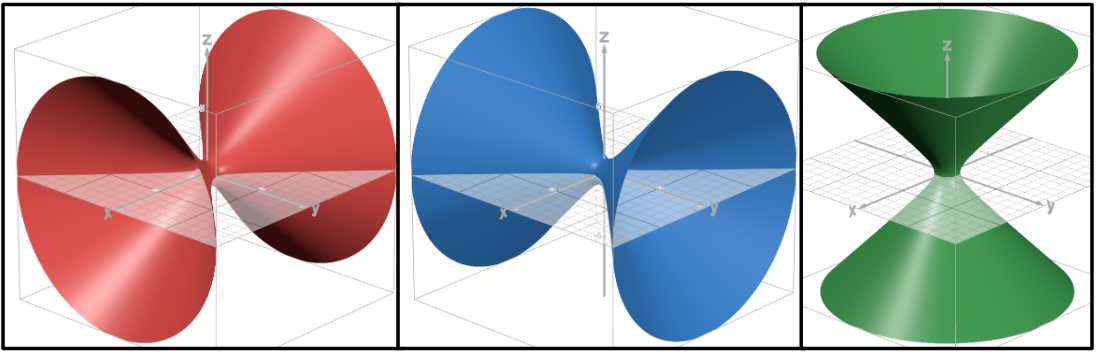
Hyperboloid of one sheet

• The variable with a negative coefficient is the axis of symmetry.

• Traces along the axis of symmetry are ellipses. Traces along the other two axes are hyperbolas.

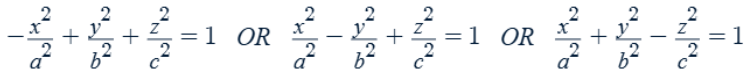
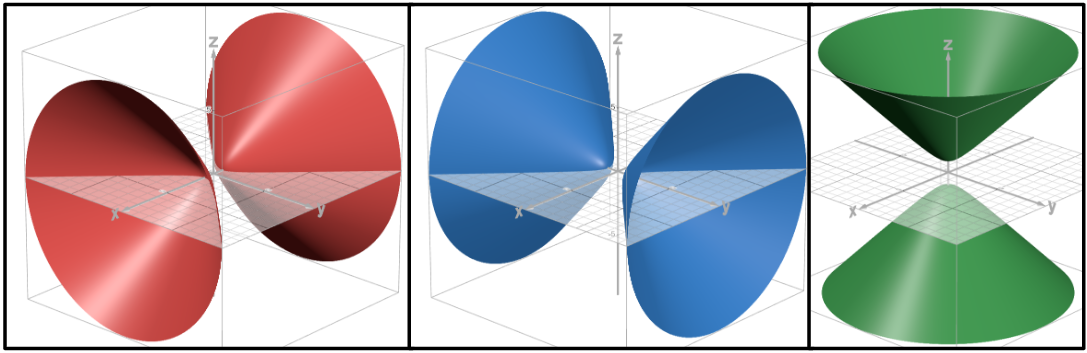
Hyperboloid of two sheets

• The variable with a positive coefficient is the axis of symmetry.

• Traces along the axis of symmetry are ellipses. Traces along the other two axes are hyperbolas.

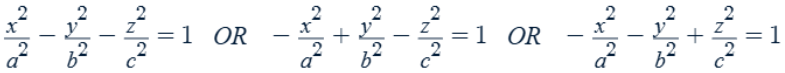
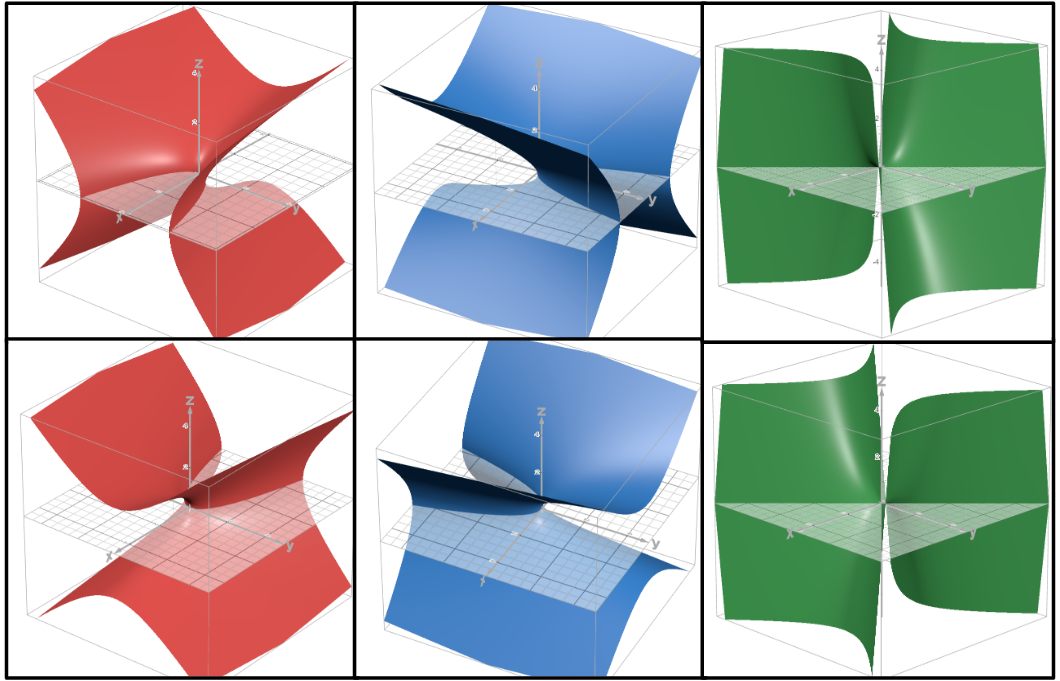
Hyperbolic paraboloid

The variable with a power of 1 is the axis along which the traces are hyperbolas. Traces along the other two axes are parabolas, opening down/back for the variable with a positive coefficient and opening up/forward for the variable with a negative coefficient.

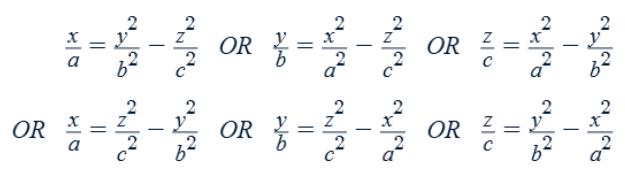
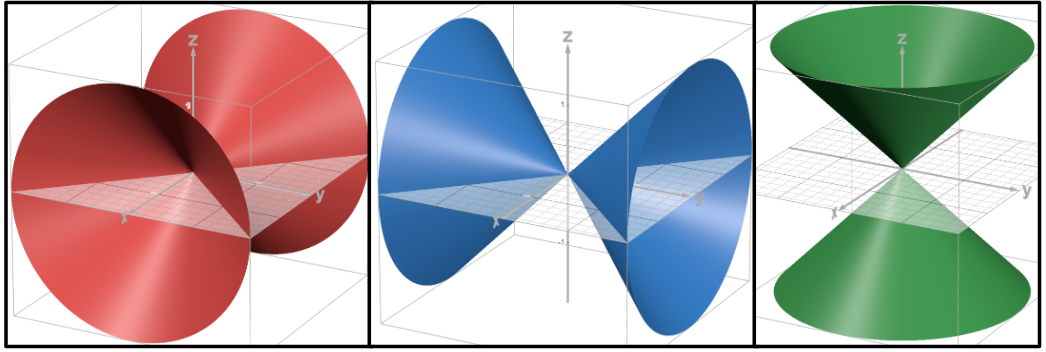
Cone

• The isolated variable is the axis of symmetry.

• The traces are the same as a hyperboloid of one sheet because the only difference in the equation is that the constant is zero instead of one.

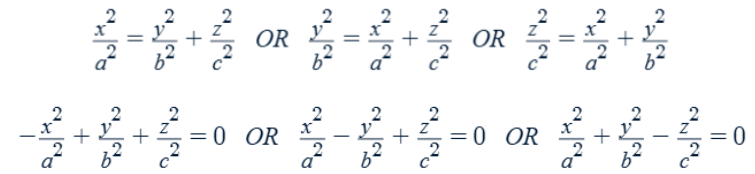
Formulas of common 2-D shapes on a ab-plane

• Circle/ellipse: a² + b² = k > 0

  • Cylinder in 3-D

  • For a circle, √k = radius, and the coefficients are equal.

• Parabola:

  • a = +b² + k (opens toward increasing a)

  • a = –b² + k (opens toward decreasing a)

• Hyperbola: a² – b² = k

Definition of a vector-valued function

A function (r(t)) for which the domain (t) is a set of real numbers, and the range is a set of 2-D (3-D) vectors

r(t) = <f(t),g(t),(h(t))> = f(t)i + g(t)j + (h(t)k)

* called component functions

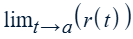
Limit of a 2-D (3-D) vector-valued function, r(t) = <f(t),g(t),(h(t))>

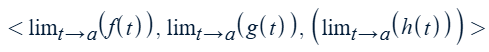
Proof a 2-D (3-D) vector-valued function,

r(t) = <f(t),g(t),(h(t))>, is continuous at t = a

i.e. direct substitution works

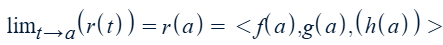
Parametric equations for a plane (space) curve with the 2-D (3-D) vector-valued function

r(t) = <f(t),g(t),(h(t))>

x = f(t)

y = g(t)

(z = h(t))

Derivative of a 2-D (3-D) vector-valued function,

r(t) = <f(t),g(t),(h(t))>

r’(t) = <f’(t),g’(t),(h’(t))>

OR

dr/dt = <dx/dt, dy/dt, dz/dt>

Unit vector T(t) in the direction of the tangent vector r’(t) to the curve

Also: r’(a) is the direction vector of the tangent line at t = a.

* You can find t = a from the tangent point and vice versa using the curve’s parametric equations.

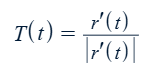
d/dt [u(t) • v(t)]

Product rule: u’(t) • v(t) + u(t) • v’(t)

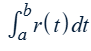
Integral of a 2-D (3-D) vector-valued function, r(t) = <f(t),g(t),(h(t))>

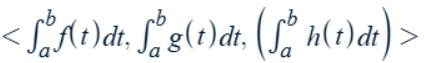
Arc length of a plane (space) curve with the 2-D (3-D) vector-valued function r(t) = <f(t),g(t),(h(t))> for a ≤ t ≤ b

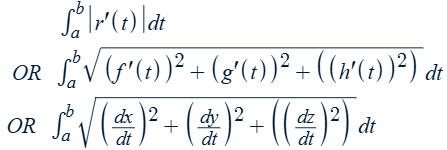
Arc length function (s(t)) of a plane (space) curve with the 2-D (3-D) vector-valued function r(u) = <f(u),g(u),(h(u))> from t = a in the direction of increasing t

Also: s’(t) = |r’(t)| OR ds/dt = |dr/dt|

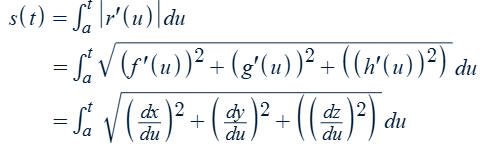
How to reparametrize a curve with respect to arc length

1. Find s(t) using the arc length formula.

2. Solve for t.

3. Substitute t for its equivalent terms of s.