Clustering

Clustering Analysis

Finding similarities between data according to the characteristics found in the data and grouping similar data objects into clusters

Cluster

A collection of data objects

Similar (or related)

another within the same group

dissimilar (or unrelated)

to the objects in other groups

Userpervised Learning

no predefined classes

Stand-alone tool

To get insight into data distribution

Data reduction

• Summarization

• Compression

Summarization

Preprocessing for regression, PCA, classification, and association analysis

Compression

Image processing: vector quantization

Application of Cluster Analysis

• Data reduction

• Hypothesis generation and testing

• Prediction based on groups

• Finding K-nearest Neighbors

• Outlier detection

Basic Steps to Develop a Clustering Task

• Feature selection

• Proximity measure

• Clustering criterion

• Clustering algorithms

• Validation of the results

• Interpretation of the results

Feature Selection

• Select infor concerning the task of interest

• Minimal information redundancy

Proximity measure

The similarity of two feature vectors

Clustering criterion

Expressed via a cost function or some rules

Clustering algorithms

 Choice of algorithms

Validation of the results

Validation test (also, clustering tendency test)

Interpretation of the results

Integration with applications

Good Clustering

A _______ method produces high-quality clusters with high intra-class similarity (cohesive within clusters) and low inter-class similarity (distinctive between clusters).

Quality

The _____ depends on the similarity measure used, its implementation, and the method’s ability to discover hidden patterns.

Dissimilarity/Similarity Metric

Quality of clustering is measured using a ________, often expressed as a distance function (e.g., metric: d(i, j))

Partitioning criteria

Single level vs. hierarchical partitioning (often, multi-level hierarchical partitioning is desirable)

Separation of clusters

Exclusive (e.g., one customer belongs to only one region) vs. non-exclusive (e.g., one document may belong to more than one class)

Similarity measure

Distance-based (e.g., Euclidian, road network, vector) vs. connectivity-based (e.g., density or contiguity)

Clustering Space

Full space (often when low dimensional) vs subspaces (often in high-dimensional clustering)

Requirements and Challenges

• Scalability

• Ability to deal with different types of attributes

• Constraints-based clustering

• Interpretability and usability

Scalability

Clusterning all the data isntead of only on samples

Ability to deal with different types of attributes

Numerical, binary, categorical, ordinal, linked, and mixture of these

Constraint-based clustering

• User may give inputs on constraints

• Use domain knowledge to determine input parameters

Major Clustering Approaches

• Partitioning approach

• Hierarchical approach

• Density-based approach

• Grid-based approach

• Model-based

• Frequent pattern-based

• User-guided or constraint-based

• Link-based clustering

Partitioning approach

• Construct various _____ and then evaluate them by some criterion, e.g., minimizing the sum of square errors

• Typical methods: k-means, k-medoids, CLARANS

Hierarchical approach

• Create a _____decomposition of the set of data (or objects) using some criterion

• Typical methods: Diana, Agnes, BIRCH, CAMELEON

Density-based approach

•  Based on connectivity and ____ functions

• Typical methods: DBSCAN, OPTICS, DenClue

Grid-based approach

• Based on a multiple-level granularity structure

• Typical methods: STING, WaveCluster, CLIQUE

Model-based

A ____ is hypothesized for each of the clusters and tries to find the best fit of that model to each other

Typical methods: EM, SOM, COBWEB

Frequent pattern-based

• Based on the analysis of frequent patterns

• Typical methods: p-Cluster

User-guided or constraint-based

• Clustering by considering _______ or application-specific constraints

• Typical methods: COD (obstacles), constrained clustering

Link-based clustering

• Objects are often linked together in various ways

• Massive links can be used to cluster objects: SimRank, LinkClus

Weakness of the K-Means method

• Applicable only to objects in a continuous n-dimensional space

• Need to specify k, the number of clusters, in advance

• Sensitive to noisy data and outliers

• Not suitable to discover clusters with non-convex shapes

Hierarchical Clustering

It is an alternative approach to k-means clustering for identifying groups in a data set.

Dendrogram

Heirachical clustering results that is visualezed using a tree-based representation.

Agglomerative clusterning

Commonly referred to as Agnes. Works in a bottom-up manner

AGNES (Agglomerative Nesting)

It is a hierarchical clustering method introduced by Kaufmann and Rousseeuw in 1990 and implemented in statistical packages like Splus. It uses the single-link method and a dissimilarity matrix to merge nodes with the least dissimilarity, proceeding in a non-descending fashion until all nodes are merged into a single cluster.

Types of Heirarchical Clustering

• Single Linkage

• Complete Linkage

Single Linkage

We merge in each step the two clusters, whose two closest memebers have the smallest distance.

Complete Linkage

We merge in the members of the clusters in each step, which provide the smallest maximum pairwise distance.

DIANA (Divisive Analysis)

Introduced by Kaufmann and Rousseeuw in 1990, is a hierarchical clustering method implemented in statistical packages like Splus. It follows the inverse order of AGNES, starting with all nodes in one cluster and progressively dividing them until each node forms its own individual cluster.

Distance between Clusters

• Single Link

• Complete Link

• Average

• Centroid

• Medoid

Single Link

Smallest distance between an element in one cluster and an element in the other, i.e., dist(Ki, Kj) = min(tip, tjq)

Complete link

Largest distance between an element in one cluster and an element in the other, i.e., dist(Ki, Kj) = max(tip, tjq)

Average

Average distance between an element in one cluster and an element in the other

Medoid

A chosen, centrally located object in the cluster

Divisive hierarchical clustering

It is a top-down hierarchical clustering method.

1. It begins with all observations in a single cluster.

2. At each step, the most heterogeneous cluster is split into two.

3. This process continues until each observation forms its own cluster.

Centroid

The middle of a cluster

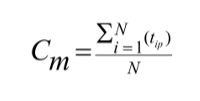
Radius

The square root of average distance from any point of the cluster to its centroid

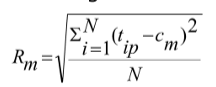
Diameter

The square root of average mean squared distance between all pairs of points in the cluster

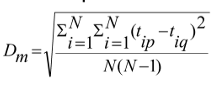
Density-Based Clustering Methods

• Clustering based on _____ , specifically _____ points.

• Major features:

  1. Discover clusters of arbitrary shapes.

  2. Handle noise.

  3. One scan required.

  4. Density parameters are needed for termination.

Two Parameters of Density-Based Clustering

• Eps: Maximum radius of the neighbourhood 

• MinPts: Minimum number of points in an Eps-neighbourhood of that point

Directly density-reachable

A point p is _______ from a point q with respect to Eps and MinPts if:

1. p is within the Eps neighborhood of q (i.e., the distance between p and q is less than or equal to Eps).

2. q has at least MinPts points within its Eps neighborhood (including q itself).

Density-reachable

A point p is _______ from a point q with respect to Eps and MinPts if there is a chain of points p₁, …, pₙ where p₁ = q and pₙ = p, such that each point pᵢ₊₁ is directly density-reachable from pᵢ.

Density-connected

A point p is density-connected to a point q with respect to Eps and MinPts if there exists a point o such that both p and q are density-reachable from o with respect to Eps and MinPts.

DBSCAN

Density-Based Spatial Clustering of Applications with Noise. It relies on a density-based notion of cluster, where a cluster is defined as a maximal set of density-connected points.

Main features of DBSCAN

DBSCAN discovers clusters of arbitrary shape in spatial databases and is capable of handling noise.

OPTICS

Ordering Points To Identify the Clustering Structure. Introduced by Ankerst, Breunig, Kriegel, and Sander in 1999 at SIGMOD.

Special order of the Database

OPTICS produces a ________ with respect to its density-based clustering structure. This cluster-ordering contains information equivalent to density-based clusterings across a wide range of parameter settings.

Key characteristics of grid-based clustering methods

This method use a multi-resolution grid data structure. Notable methods include:

• STING (Statistical Information Grid) by Wang, Yang, and Muntz (1997)

• CLIQUE by Agrawal et al. (SIGMOD’98) — supports both grid-based and subspace clustering

• WaveCluster by Sheikholeslami, Chatterjee, and Zhang (VLDB’98) — employs a multi-resolution clustering approach using wavelet methods.

STING (Statistical Information Grid Approach)

Authored by Wang, Yang, and Muntz (VLDB’97).
Key Features:

• The spatial area is divided into rectangular cells.

• Multiple levels of cells correspond to different levels of resolution.

Key Features of the STING clustering method

• Cell Hierarchy

• Statistical Infomration

• Top-Down Approach

STING Advantages

• Query-independent.

• Easy to parallelize.

• Incremental updates possible.

• Time complexity of O(K), where K is the number of grid cells at the lowest level.

STING Disadvantages

All cluster boundaries are either horizontal or vertical; diagonal boundaries are not detected.

CLIQUE (Clustering In QUEst)

Authored by Agrawal, Gehrke, Gunopulos, Raghavan (SIGMOD’98). Automatically identifies subspaces of high-dimensional data space for improved clustering compared to the original space. Considered both density-based and grid-based.

External Measures

• Supervised measures that use criteria not inherent to the dataset.

• Compare a clustering against prior or expert-specified knowledge (ground truth) using specific quality metrics.

Internal Measures

• Unsupervised measures derived from the data itself.

• Evaluate clustering quality based on cluster separation and compactness (e.g., Silhouette coefficient

Matching-Based Measures

• Purity

• Maximum Matching

• F-Measure

Entropy-Based Measures

• Conditional Entropy

• Normalized Mutual Information (NMI)

• Variation of Information

Pair-Wise Measures

• True Positives (TP)

• False Negatives (FN)

• False Positives (FP)

• True Negatives (TN)

• Jaccard Coefficient

• Rand Statistic

• Fowlkes-Mallows Measure

Correlation Measures

• Discretized Huber Statistic

• Normalized Discretized Huber Statistic