Econ3220 Lecture 3: Theories of Economic Growth & Development Part 2

What is the cornerstone of Solow's neo-classical growth theory?

Increasing the rate of capital accumulation (K-accumulation).

How does the Solow model differ from the Harrod-Domar model?

It includes population growth and technological progress.

What is the cornerstone of Solow's neo-classical growth theory?

Increasing the rate of capital accumulation (K-accumulation).

How does the Solow model differ from the Harrod-Domar model?

It includes population growth and technological progress.

What are the assumptions of the Solow model with constant technology?

Closed economy, two factors of production (K and L), constant returns to scale, constant population growth, no tech change, no public saving, private saving proportional to income

What is the production function in the Solow model?

Y(t) = f[K(t), L(t), A(t)] where A(t) is technology.

What does the fundamental equation of the Solow model show?

Change in capital per worker = savings per worker - (depreciation + population growth) * capital per worker.

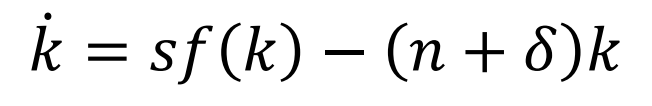
What is the condition for a steady state in the Solow model?

When savings per worker equals effective depreciation: sf(k) = (n + δ)k.

What happens to per capita variables in the steady state of the Solow model?

They become constant; no per capita growth. k* is constant as k-dot=0; y* is constant as y*=f(k*); c* is constant as c*=(1-s)•f(k*)

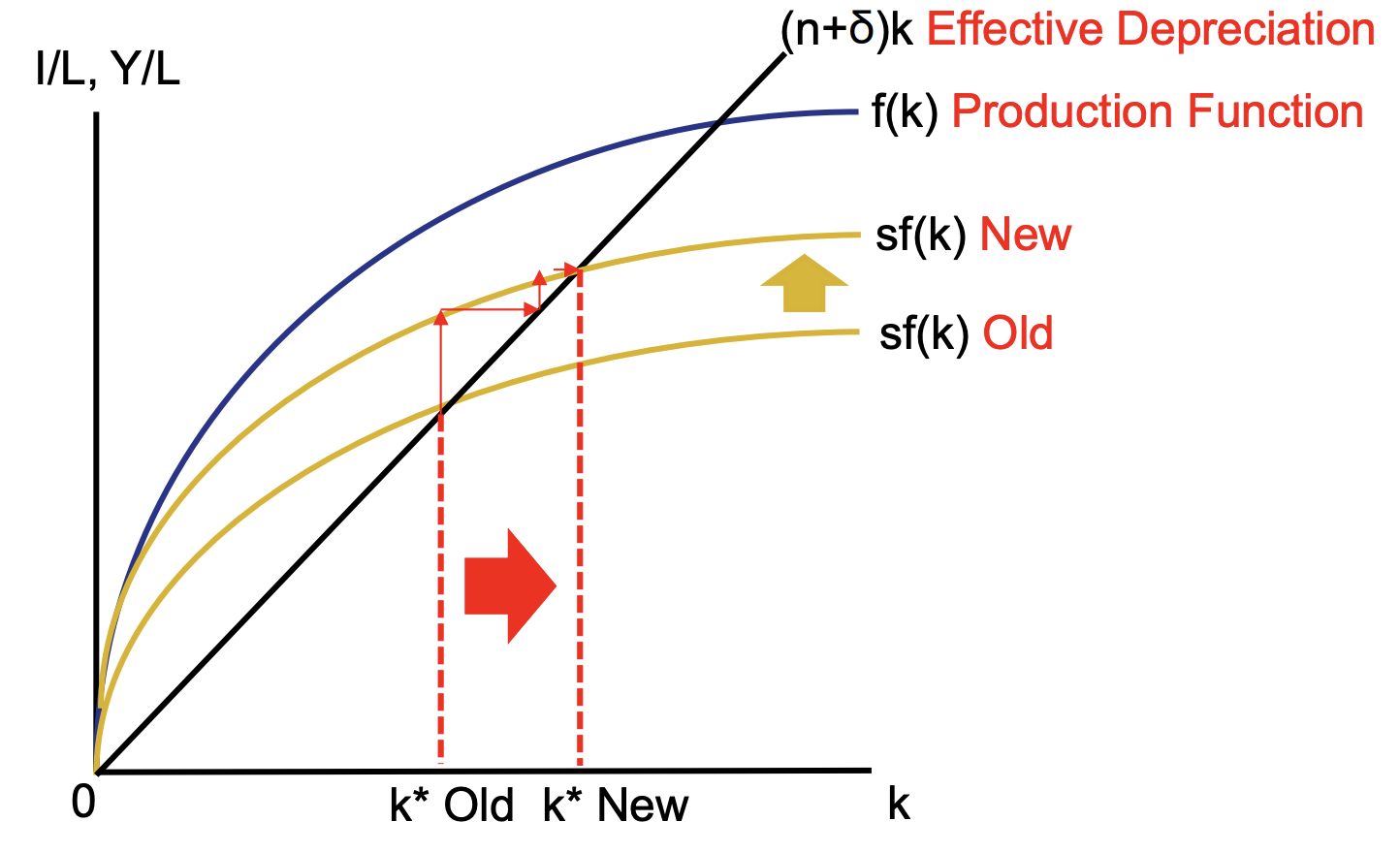
What does an increase in the savings rate do in the Solow model?

It raises the steady-state level of capital per worker by pivoting out the gross investment function, leading to higher output per worker.

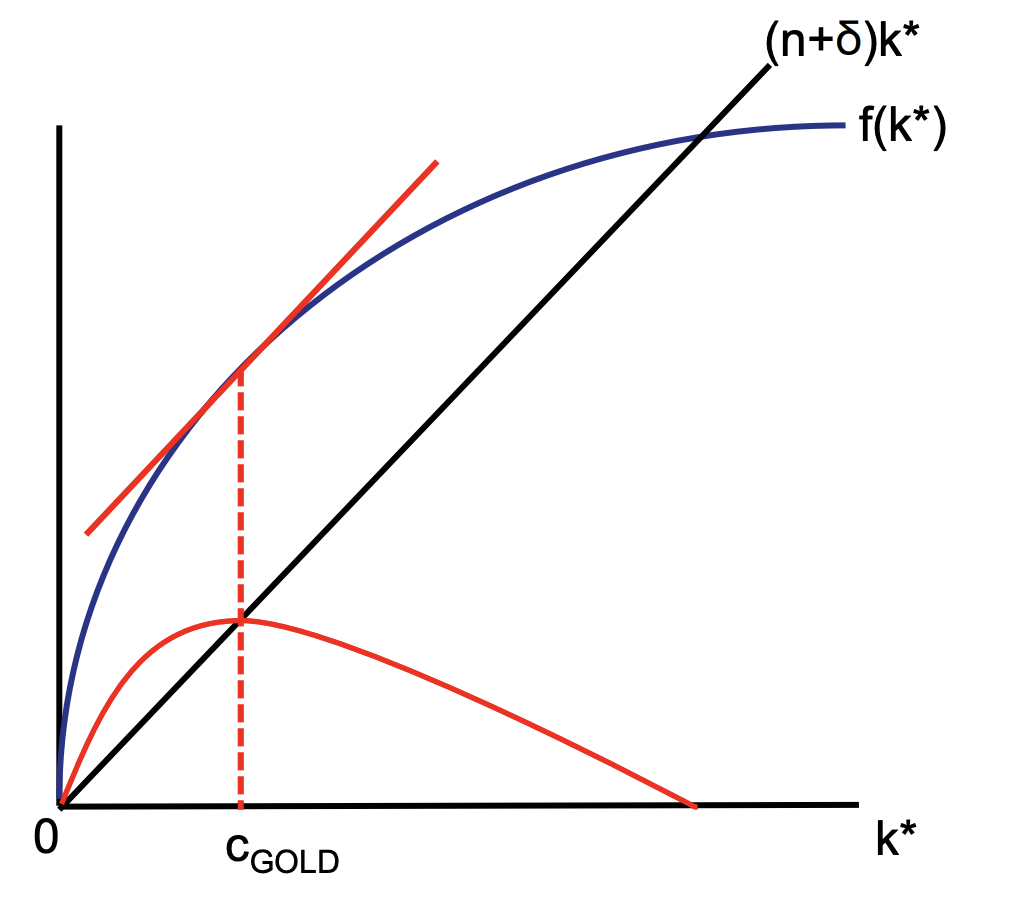
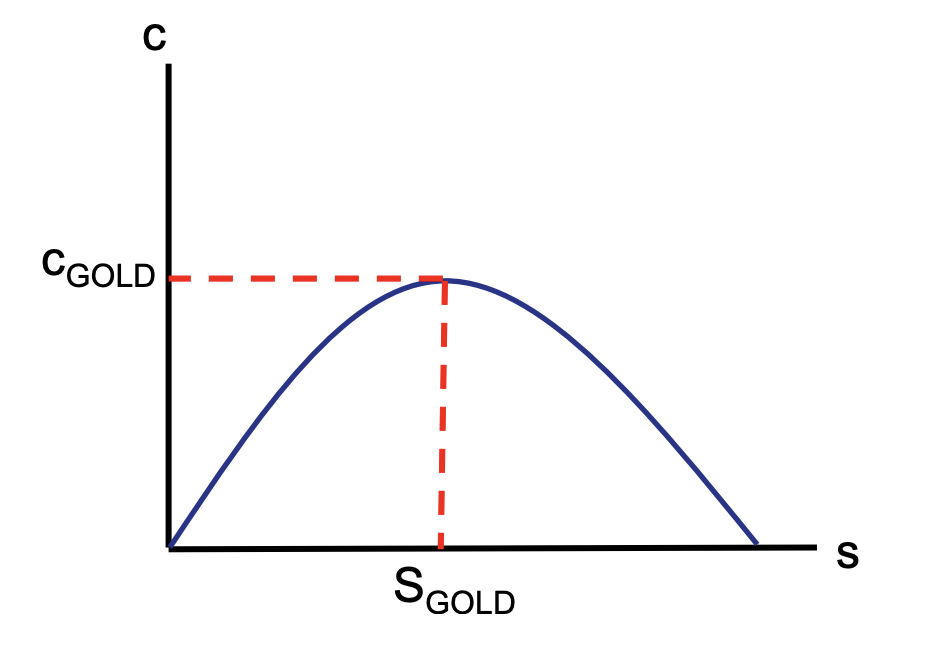
What is the 'Golden Rule' level of capital accumulation?

The level of capital that maximizes steady-state consumption per worker. Consumption in steady state is c*=f(k*)-(n+δ)k*; maximise c* and set equal to 0 𝒇’(𝒌*) = 𝒏 + 𝜹; therefore set k=k-gold where the slope of the production function = slope of the depreciation curve c-GOLD=f(k-GOLD) - (n+δ)kGOLD

What are the counterveiling forces of savings on consumption

1. Higher s increases y*, therefore increasing c*

2. Higher s reduces (1-s), therefore reducing c*

What is the Golden Savings rate

When golden consumption equals golden savings. It’s an inverted U shape, increases in savings leads to an increase in consumption to a point, then consumption decreases.

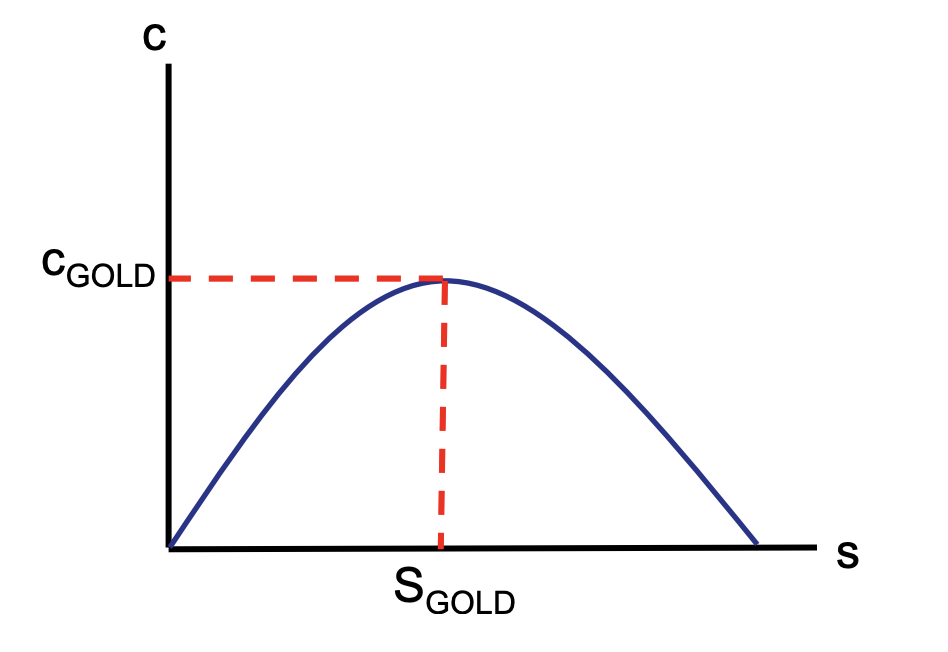
What is dynamic inefficiency in the Solow model?

When the savings rate is above the Golden Rule rate, leading to lower consumption than possible. Also when f’(k) < n+σ

What role does technology play in long-run economic growth?

Sustained per capita growth requires technological progress. Without technological progress, per capita growth stops due to diminishing returns to K

What is meant by 'exogenous technology' in the Solow model?

Technology grows at a given constant rate, not influenced by economic factors.

What is the Solow paradox

Technological progress is key to sustained per capita growth, however, technology is assumed to be constant

What is Harrod-neutral technological progress?

Labour-augmenting technological progress (increasing labour productivity) that keeps factor shares constant.

What growth rate do level variables (Y, K, C) achieve with exogenous tech progress?

They grow at the rate of (n + x), where x is the rate of tech progress.

Why does the capital-labour ratio reach a unique steady-state value?

Because of diminishing returns to capital and constant effective depreciation.

Solow Model

A neoclassical model of economic growth that explains long-run economic growth based on capital accumulation, labor or population growth, and increases in productivity, typically exogenously driven.

Capital Accumulation

The growth of capital resources, including human capital and physical capital.

Steady State

A condition in the Solow model where all per capita variables are constant and the economy grows at a constant rate.

Golden Rule Level of Capital

The level of capital that maximizes consumption per worker in the steady state.

Dynamic Inefficiency

A situation in which the economy saves too much, leading to lower consumption than possible.

Exogenous Technological Progress

Technological growth that is determined outside the model and is not explained by the model itself.

Harrod-neutral Technological Progress

Labour-augmenting technology that does not change the capital-output ratio or factor shares.

Inada Conditions

Conditions that ensure diminishing returns to capital and prevent the economy from exploding or collapsing.

Effective Depreciation

The sum of the depreciation rate and the population growth rate, affecting the amount of capital needed to maintain the capital-labour ratio. (𝑛 + 𝛿)𝑘

Transition Dynamics

The process through which an economy moves from one steady state to another due to changes in parameters like savings or depreciation.

What are Kaldors growth theories

1. Output per head, y, grows over time, and its growth rate does not tend to diminish

2. The capital labour ratio, K/L, tends to grow over time.

3. The rate of return to capital, r, is roughly constant.

4. The capital output ratio, K/Y, is roughly constant.

5. The shares of capital and labour, α and 1 − α, respectively, are roughly constant.

6. The growth rate of y differs substantially across countries