Joint Random Variables

What are joint random variables?

Two or more random variables, discrete or continuous in any combination, that represent events/outcomes occurring in connection with each other, as in the AND logical relationship.

What is a Joint PMF?

When the two joint random variables are discrete, we use a PMF represented by:
pX,Y(xi,yi) = P(X = xi and Y = yi).
Instead of a regular single-random variable PMF describing the probably mass placed on each outcome, a Joint PMF describes the probability mass placed on each possible pair of outcomes (x,y).

What is a Joint PDF?

When the two joint random variables are continuous, we use a PDF represented by:
P(a ≤ X ≤ b, c ≤ Y ≤ d) = ∫^bva ∫^dvc (fXY(x,y)) dydx
This describes the likelihood of two contentious random variables taking on a particular range of values, as with regular PDF.

What is Joint CDF?

When the one joint random variable is discrete, and the other is continuous, we use a CDF represented by:
FXY(x,y) = P(X ≤ x and Y ≤ y).
This equation gives the cumulative probability of the event that X is most x and Y is most y.

What are multi-variate random variables?

When a circumstance can be described by more than two random variables, we use multivariate probability distributions.

What is the Multivariate PMF?

Simply when we extend Joint PMF to encompass more discrete random variables.
f(x1, x2, …, xn) = P (Xn = xn).

What is Multivariate PDF?

Simply when we extend the concept of Joint PDF to encompass more than two continuous random variables.
P(a1≤X1≤b1…an≤Xn≤bn) = ∫^b1va1…∫^bnvan (f(x1,…xn) dxn…dx1

If we need to explore X and Y separately during a joint probability distribution, what do we look for?

Marginal probabilities! The goal is to remove one variable from the probability distribution.

What is a discrete marginal probability function?

When both joint random variables are discrete and have outcomes in the range R and S respectively.

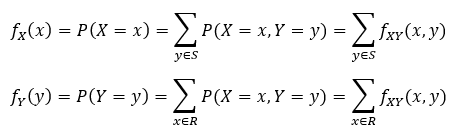
What is a discrete conditional distribution?

Sometimes an event has happened already, and we want to model what will happen next. When both joint random variables are discrete and have outcomes in the range R and S respectively, and when fx(x) > 0 (aka. we assume X=x has happened/is possible), then the following is true.
The properties of PMF apply.

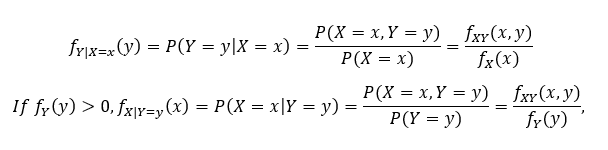
What is a continuous marginal probability distribution?

If X and Y are continuous random variables, we might still want to examine them separately.

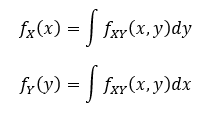
What is a continuous conditional probability distribution?

Assuming fX(x) > 0 (meaning X = x is possible/has occurred), then the following apply. The properties of PDF apply.

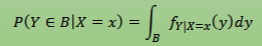
How do you obtain multivariate marginal probability distributions?

We do this by integrating out other variables. So for f(x,y,z,a,b) for random variables X, Y, Z, A, B, the marginal distribution of fYA on random variables Y and A can be obtained as follows:

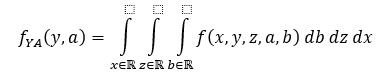
What is the expected value for a discrete joint random variable?

E(X) = μX = ∑v(x∈R) x fX(x)

What is the variance of a discrete joint random variable?

V(X) = ∑v(x∈R) x² fX(x) - (E(X))²

What is covariance? And what is the equation to find the covariance of joint discrete/continuous random variables?

Covariance measures the strength of a linear relationship between two random variables. For discrete or continuous:
cov(X,Y) = E[XY] - E[X]E[Y]

What is the correlation coefficient?

The correlation coefficient normalises the covariance so that the strength of a linear relationship can be represented by ρ, which is always a value between -1 and 1.
If X and Y are independent, ρ(X,Y) = 0
If X and Y are dependent, ρ(X, Y) ≠ 0.