Normal and Standard Normal Distribution in ECO 391

Discrete Random Variables

Countable variables with distinct values.

Continuous Random Variables

Uncountable variables with infinite values.

Normal Distribution

Symmetric, bell-shaped distribution with total area 1.

Standard Normal Distribution

Normal distribution with mean μ=0 and σ=1.

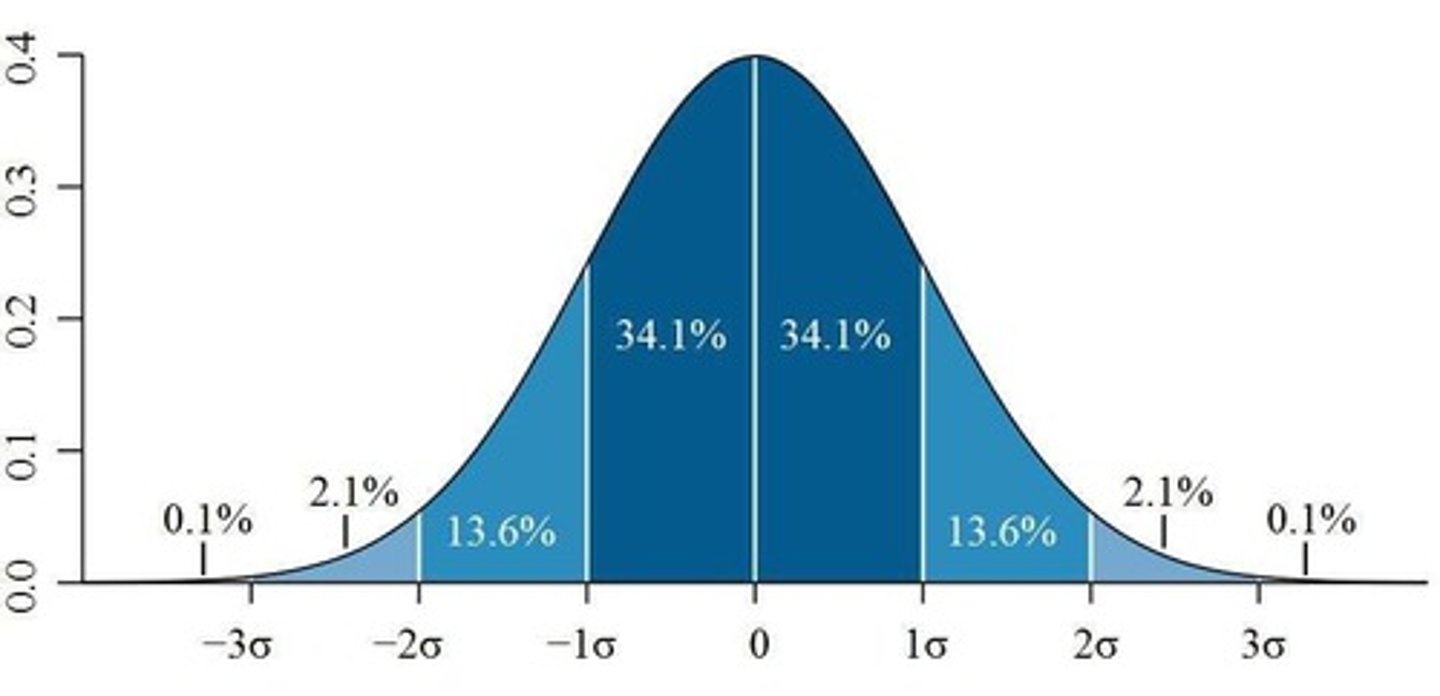
Empirical Rule

68-95-99.7 rule for normal distributions.

Z-score

Standardized score indicating number of standard deviations.

T-score

Standardized score used with sample standard deviation.

Mean

Average value of a data set.

Median

Middle value when data is ordered.

Mode

Most frequently occurring value in data.

Asymptotic

Tails approach axis but never touch.

Z-score Formula

Z = (X - μ) / σ.

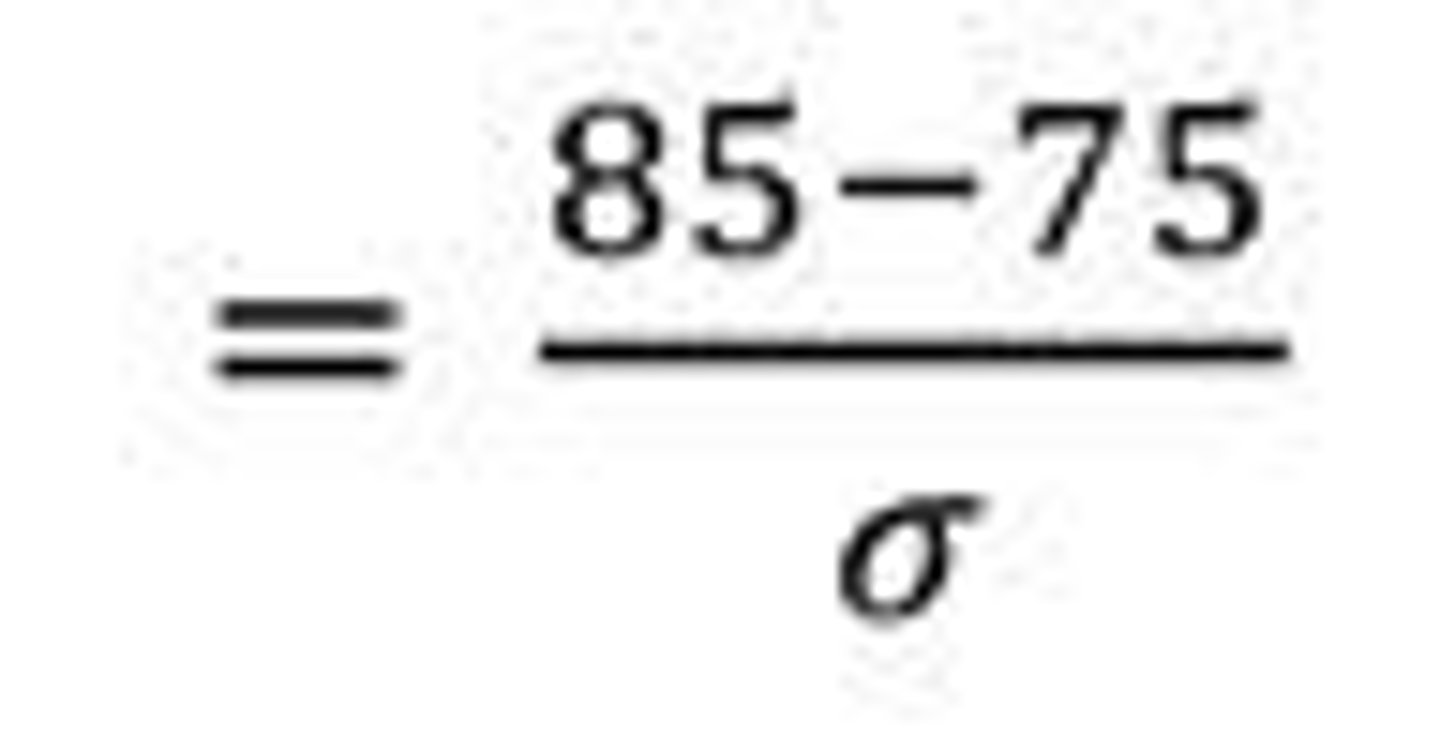
T-score Formula

t = (X - μ) / (s/√n).

Standard Deviation (σ)

Measure of data dispersion around the mean.

Sample Standard Deviation (s)

Estimate of standard deviation from sample data.

Normal Distribution Curve

Graphical representation of normal distribution.

Bell-shaped Curve

Characteristic shape of normal distribution graph.

Total Area Under Curve

Equals 1 for probability distributions.

Probability

Likelihood of an event occurring.

Random Variable

Variable whose values depend on chance.

X-value

Original value before transformation to Z or T.

Z-value

Value after standard transformation from X.

Probability

Likelihood of an event occurring, expressed as a decimal.

Z-score

Standardized score indicating how many standard deviations from the mean.

Normal Distribution

Symmetrical distribution where most values cluster around the mean.

Mean (μ)

Average value of a set of data points.

Cumulative Probability

Probability that a random variable is less than or equal to a certain value.

Z-table

Table showing cumulative probabilities for Z-scores.

Right Tail Test

Test assessing the probability of extreme values on the right.

Standard Normal Distribution

Normal distribution with mean 0 and standard deviation 1.

Area under the curve

Represents total probability in a probability distribution.

1σ Range

Approximately 68% of data falls within one standard deviation.

2σ Range

Approximately 95% of data falls within two standard deviations.

3σ Range

Approximately 99.7% of data falls within three standard deviations.

Discrete Random Variables

Variables with countable distinct values.

Continuous Random Variables

Variables with uncountable values within intervals.

Negative Z-score

Indicates a value below the mean.

Right Tail Probability

Probability of observing values greater than a certain score.

Less than 84 kg

Condition representing 1σ below the mean weight.

Between 73 and 117 kg

Condition representing 2σ around the mean weight.

More than 128 kg

Condition representing 3σ above the mean weight.

Z-score

Number of standard deviations from the mean.

Standard Normal Distribution

Normal distribution with mean 0 and SD 1.

Probability P(Z > 1)

Calculated as 1 - P(Z ≤ 1).

Standard Deviation (σ)

Measure of data dispersion from the mean.

P(Z ≤ 1)

Probability Z is less than or equal to 1.

P(Z > 1.6)

Probability Z is greater than 1.6.

Normal Distribution

Symmetrical distribution where mean = median = mode.

Probability of Z < -2

Equivalent to P(Z > 2) due to symmetry.

Average Return

Mean return of an investment portfolio.

Balanced Portfolio

Investment strategy diversifying across asset classes.

Z = (X - μ) / σ

Formula to calculate Z-score.

P(Z ≤ -1.92)

Probability Z is less than -1.92.

68.26%

Percentage of data within 1 standard deviation.

15.87%

Percentage of data below one standard deviation.

2.28%

Percentage of data above two standard deviations.

Average Rent

Mean monthly rent in a city.

Normal Distribution of Rent

Assumes rent values follow a bell curve.

Probability of Rent > $2,000

Calculated using standard deviations from the mean.

Z-score for 48 minutes

Calculated as 1.6 for task completion time.

Standard Deviation of Rent

Measure of rent variability in the city.