3: Dimensional Analysis by Covariance

Point cloud

A collection of points - a discrete subset of points within a space.

Euclidian Space (Cartesian Space)

Finite-dimensional, metric vector space of all n-tuples (vectors) of real values.

Metric

The ability to measure the distance between points in the space.

Confidence Interval

The probability that the real model matches the data.

Regression Analysis

Produces an equation that describes the relationship between two variables.

Correlation Analysis

Produces a value that summarises the strength of the relationship between variables.

Additive Linear Model

Relates a single dependent dependent variable to j independent variables.

• Y_i = B_iX_ji + … + B₁X_i1 + B₀ + e_i

Simple Regression Model

A regression model that takes only one independent variable into account (j = 1)

Multiple Regression Model

A regression model that takes more than one independent variable into account (j > 1)

Multiple Regression - Error Rate

If there’s too many parameters in the model, the possibility of an error appearing increases - you have to match more observations.

Residual

The difference between a predicted value and the real observation of the value.

Dispersion (Spread)

The extent to which a stochastic variable varies around a mean value.

Covariance

A way to measure dispersion.

Covariance Formula

• E(…) is the expected value of the probability distributions.

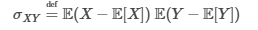
Covariance Formula (Unbiased Estimator)

• n is the number of observations

• x_i and y_i are the observations in general and flat x and y are the means for X, Y respectively.

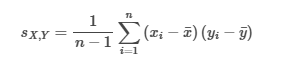
Covariance - above zero

When X grows, Y also grows.

Covariance - below zero

When X grows, Y shrinks.

Covariance - close to zero

No discernable trend in the data.

Variance

Covariance of a variable against itself.

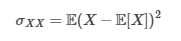
Unbiased Variance Estimator

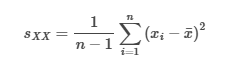
Eigendecompositions

A factorisation of a matrix into canonical form, represented in eigenvalues and eigenvectors.

Eigenvector Notation

Aq = λq, (A - λI)q = 0

• A is a transformation matrix.

• λ is the eigenvalue.

• q is the eigenvector.

Solving for eigenvalues

Solve for λ with det(A - λI) = 0.

Determinent (det(x))

Given a matrix:
a b

c d

a * d - b * c