Shortest Paths in Graphs

Paths

Between nodes 𝑢 and 𝑣:

• Sequence of (non-repeating) nodes: 𝑢, 𝑤1, 𝑤2, … , 𝑣

• In the example, (1,2,3,5,4) is one between 1 to 4

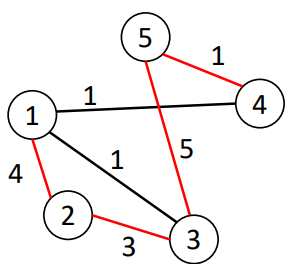
Shortest Paths

between nodes 𝑢 and 𝑣 = among all paths between u and v, the one that has the smallest total edge weight

Shortest Paths in Unweighted Graphs

Consider an unweighted graph 𝐺

BFS search can compute shortest paths when 𝐺 is an unweighted graph

BFS tree contains shortest paths from ss to any node in G, when G is an (edge) unweighted graph

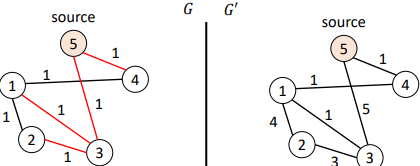
Shortest Paths in Weighted Graphs

The sum of weights on that path should be smaller than the sum of weights on any other path

• from source (5) to node 3 in G? (5,4,1,3) or 5 -> 4 -> 1 -> 3

• when you consider weights (or distances), not hops

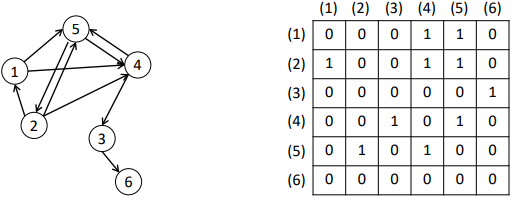
BFS Traversal on Directed Graphs

Consider a directed, unweighted graph 𝐺. Compute BFS tree rooted at 4

BFS tree spans all nodes because all nodes can be reached from 4

When the graph is not strongly-connected, the BFS may not visit all nodes

Why does BFS not work on Weighted Graphs?

it doesn’t take edge weights into account

Computing Shortest Paths in Weighted Graphs

Use Dijkstra’s algorithm to solve the three shortest path problems

1. Shortest distances (from source)

2. Shortest paths (from source)

3. Pathfinding (from source)

Linked to network routing protocols or robot exploration (or search) algorithms

Several extensions:

• A* search algorithm

• Bellman-Ford algorithm

• Floyd-Warshall algorithm

Dijkstra’s Algorithm

Keep two arrays: visited[] and distanceToSource[]

1. Start at source, and initialize:

   • Initialize visited status of all nodes (besides source) to unvisited

   • Initialize distances to source to ∞ for all nodes (except source), and to 0 for the source

2. While not all nodes have been visited:

   • Visit (unvisited) node 𝑣 with smallest distanceToSource

   • For all neighbours of 𝑣, if the path going through 𝑣 is shorter, then update distance

     • For visited node 𝑣 and neighbour 𝑢:

     • If distToS[u] > distToS[v] + weight(u,v), then distToS[u] = distToS[v] + weight(u,v)

3. Return distanceToSource

Some intuition on Dijkstra’s

1. At the start, and through most of the algorithm, these are “approximate distances”

   • ∞ implies the node is “very far”, or more precisely unreachable,

   • 0 implies the node is the source

2. The key idea of Dijkstra’s algorithm is to improve these approximations, as you visit more and more nodes, until all distances to the source are accurate

3. (Invariant) When a node is visited, their distance to the source is accurate

Shortest Path with Dijkstra’s

Keep three arrays: visited[], previousNode[] and distanceToSource[]

1. Start at source, and initialize:

   • Initialize visited status of all nodes (besides source) to unvisited

   • Initialize distances to source to ∞ for all nodes (except source), and to 0 for the source

   • Initialize previousNode's entries to null

2. While not all nodes have been visited:

   • Visit (unvisited) node 𝑣 with smallest distanceToSource

   • For all neighbours of 𝑣, if the path going through 𝑣 is shorter, then update distance and set previousNode[neighbour] to 𝒗

3. Return distanceToSource and previousNode

Pathfinding with Dijkstra’s

1. While not all nodes have been visited:

   • Visit (unvisited) node 𝑣 with smallest distanceToSource

   • If current visited node is the target node, return distanceToSource[v] and pathToSource[v], where pathToSource[v] = (previousNode[v], previousNode[previousNode[v]], …)

   • For all neighbours of 𝑣, if the distance of the path going through 𝑣 is a better approximation, …

2. Throw an exception: “target node not found”

Dijkstra’s Algorithm Complexity

Worst-case time complexity of 𝑶(𝒏^𝟐):

• We visit each node once, and during each visit, we do 𝑂(1) operations per neighbours

• This amounts to 𝑂(𝑚) operations where 𝑚 is the number of edges

• And to get each new visited node, we find the unvisited node with minimum distance to source, which takes 𝑂(𝑛) operations

• In total, this amounts to 𝑂(𝑛^2) operations

We can use better data structures (priority queues based on Fibonacci heaps, or self-balanced binary search trees, or other heaps) to improve Dijkstra’s algorithm to:

• 𝑶(𝒎 + 𝒏 log 𝒏) worst-case time complexity

Better Shortest Path Algorithms and when to use them

1. When we have extra information (heuristic) on distances from some nodes to source, we can use the A* algorithm

2. If we have edges with negative weights (but not negative cycles) then you can use Bellman-Ford

3. If you are fine with approximating the distances (or getting some “almost” shortest paths), then there are faster algorithms…

A* Search Algorithm

• For pathfinding only (from specified source to specified target), not from the source to all other nodes

• Core idea: use heuristics (on the distance from current node to specified target) to guide (i.e., be more efficient in) the search

  • For example, if graph weights represent Manhattan distances (e.g., driving along roads)

  • Then the heuristics could be straight-line distance (e.g., distance as the bird flies)

• If 𝑑(𝑣) is the estimated distance from source to 𝑣 in Dijkstra’s algorithm, and ℎ(𝑣) the heuristic distance from node 𝑣𝑣 to the target, then in A* we compare the values:

  • 𝑑(𝑣) + ℎ(𝑣)

Bellman-Ford

• Computes shortest path from specified source to all other nodes (like Dijkstra’s algorithm)

  • Works for wider class of graphs, as it can work for (some) graphs with negative weights

  • Still, a major problem if there is a negative cycle (with negative total weight sum)

  • When there is a negative cycle, Bellman-Ford finds that cycle (but not all shortest paths)

• Core idea (like Dijkstra’s algorithm): compute (over)estimations of the distances from the source to all other nodes, which you iteratively improve upon (or relax)

  • In Dijkstra’s algorithm, you use a priority queue to decide which edge to relax,

  • In Bellman-Ford, you relax all edges every iteration, for a total of 𝑛 − 1 iterations

• Worst-Case Time Complexity: 𝑂(𝑛 ⋅ 𝑚)