Biostatistics for the Health Sciences - Everything for 1st Test

Nominal

order of categories irrelevant (also called unordered)

Ordinal

order of categories is meaningful (also called ordered)

Binary

Special case of categorical variable - only 2 possible values (also called dichotomous)

Discrete

Values equal to integers

Continuous

Values on a continuum

Is nominal data categorical or ordinal?

Categorical

Is blood type categorical or ordinal

Categorical

Is died of cancer binary or nonbinary

Binary

What are types of categorical data

Nominal, ordinal, binary

What are types of quantitative data

Discrete and continuous

Continuous examples

Blood pressure

Weight

Age

Lead

Quantitative examples

Number of babies out of 100 births who have low birth weight

Number of admissions to the emergency room

For a discrete variable, it isn’t sensible to

consider a value between two numbers (e.g. 1.5 heart attacks doesn’t make sense)

Although a continuous variable may be measured in whole numbers, it is still sensible

to consider a value between two numbers (age – 16.5 years old)

A quantitative measurement may be categorized and treated as a categorical variable

for the purpose of summaries (>25 years etc.)

Categorical variables are sometimes called ____, especially in stats classes

factors

A categorical with inherent logical ordering (age brackets) may be treated as

nominal in some analysis

Categorical data is usually summarized by:

• The proportion (percent) of observations in each of the categories

• The number in each category (frequency / count)

• Important to provide the totals (denominators of percentages)

• N or n is often used to represent the total

• N = sample size

Pie graphs represent a

categorical variable pictorial

Pie graphs display

data as a percentage of the whole

Pie graphs require

proportional reasoning

Pie graphs are especially difficult with

Ordinal data

Pie graphs are

not the best way to summarize data, but are common in media/non-expert reports

Pie graphs are most appropriate

And better when

When the aim is to convey the relative size of the parts of a whole

Better when there are not too many categories (3-7)

Bar graphs present a

summary measure for each category by a bar

BARGRAPHS: For an ordinal categorical variable, order the bars

in the order of the categories

BARGRAPHS: For a nominal categorical variable, choose

an ordering that aids understanding (for ex, alphabetical or lowest to highest)

For quantitative data, we are usually interested in

The distribution of the observations

• What are the most common or average values (center of the data?)

• How spread out are the data? (variability of the data)

• Are there some values far from the bulk of the data (outliers?)

Strategies for distribution of quantitative data

• Visualize the distribution of the data with a graph

• Summarize key aspects of the distribution with descriptive statistics, numerical descriptions of the center and spread of the data

Bar graphs can be

Stacked

Stacked bar graph methods

Can do totals, percent out of 100, or other

The histogram is a

graphical display of the distribution of quantitative data

Histogram: Horizontal scale (x) corresponds

to the values of the quantitative variable

Histogram: The x-axis is broken into a

contiguous series of sub-intervals (“classes” or “bins”)

Histogram: Bars are drawn that indicate the

frequencies or percentages of observations within each interval

Histogram:

• The area of each bar corresponds to the number of observations in each bin

• If all bins have same width, then heights of the of bars also correspond to the number of observations in each bin

Information from a histogram

• Typical values

• How much variation is present

• Shape of the distribution

• Unusual or outlying values

• Approximate frequency or percentage in a given range

Histograms can be sensitive to bin width (or cut-points)

Rule of thumb:

use number of bins = square root of number of observations

In a histogram, each observation is given

one unit of area

With unequal bin widths, easier

to use a bar graph

• Unequal intervals are really a

• Similarly for ordinal variable, more common to use term

• bar chart – does not necessarily show shape of distribution

• bar chart (concept of the distribution not the same as for quantitative variables)

We reserve the term histogram for

quantitative variables

Opposite of everyday use

One difference between histogram and bar-graph is that the number of observations is shown

by the area under the curve, or the integral of the category

Reason would have longer data is

less observations

If you have the data, use

equal size bins

In a proper histogram, each observation is

given one unit of area so the histogram reflects the shape of the distribution

In a bar graph, observations may not always be given the same unit of area so the bar graph

may not reflect the shape of the distribution

Histogram needs to show

SHAPE OF DISTRIBUTION!! (not equal sized bins)

Histograms for

quantitative data and to represent shape

Similarly for ordinal variable, more common to use the

term bar chart

We will reserve the term histogram for

quantitative variables

Stem and leaf plot:

another graph for quantitative data;

STEM AND LEAF:

Decimal point is 1 digit to the left of |

(S&P) 0 | 2 2 3 =

0.02, 0.02, 0.03

Numerical summaries for quantitative data

Central tendency and variation

Central tendency

The “middle” of the data

Variation

How “spread out” the data is

X bar

average/mean

Median

Middle point; half bigger half smaller

Mode

Most common value in the dataset

X bar = formula

(summation i=1 to n (Xsubi)) over n

Xsubi means the ith ordered observation in the data

Reasons why something can be the mode in a lead detection study

Lowest point to be detected could be why

Mean is sensitive to

Outliers

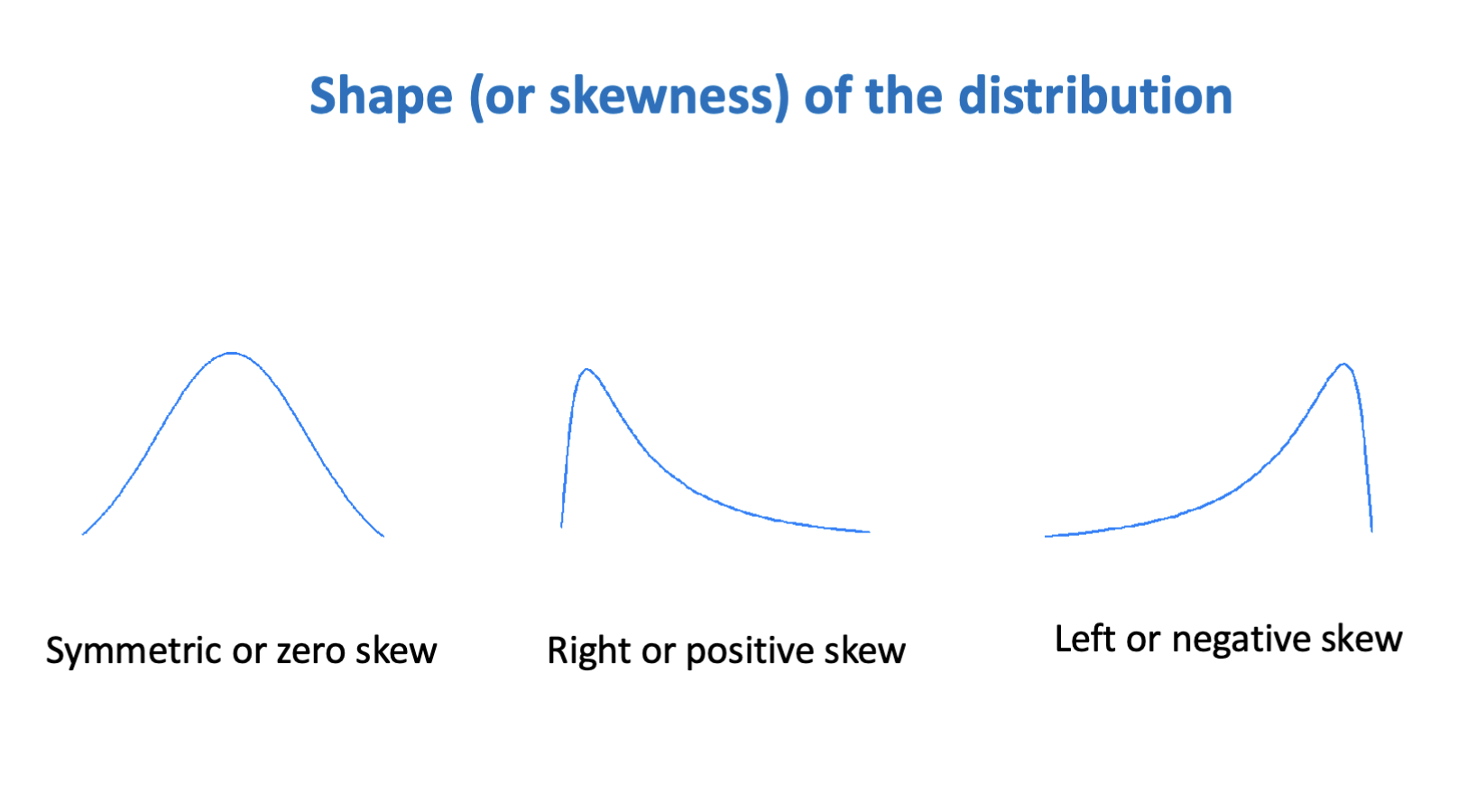
For right (positively) skewed data:

mean > median

For left (negatively) skewed data:

median > mean

Median is ___ to outliers

resistant

If symmetrical

Mean=median

Range

Smallest and largest, sometimes shown as difference between them

Interquartile range

25th and 75th percentiles, sometimes shown as difference between them

Computing IQR for 25th percentile

33 x .25.= 8.25, choose the 9th value

Value with 25% of data below it

Range and standard deviation

are sensitive to outliers

IQR is

less sensitive to outliers

B&W: top of box =

75th percentile

B&W: line in middle of box =

median

B&W: line in bottom of box =

25th percentile

B&W: whisker at top

largest value less than Q3 + 1.5 IQR

B&W: whisker at bottom

Smallest value greater than Q1 - 1.5IQR

B&W: dots

Outliers

Can use ___ box plots to show categories

Side by side

Cumulative incidence

Is the proportion (fraction) of individuals newly acquiring the disease (outcome) over a specified period of time

Cumulative incidence =

number of new cases / number at risk

Contingency table

Summarizes the information from two categorical variables (think treatment, cold-yes, cold-no, and total)

Risk factor

Variable that may increase or decrease the chance (risk) of outcome

Difference between treatment, risk factor, and exposure

Treatment is just type, but can be risk factor if it increases/decreases risk; exposure is just whether they were exposed (and would curtail exposed / unexposed categories)

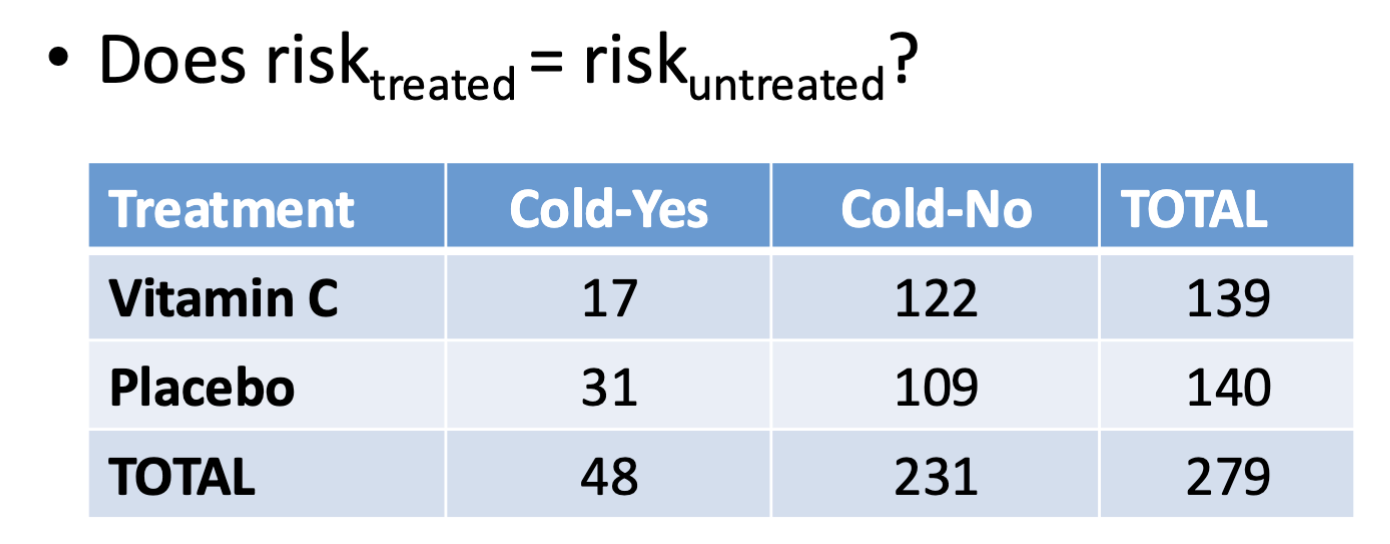
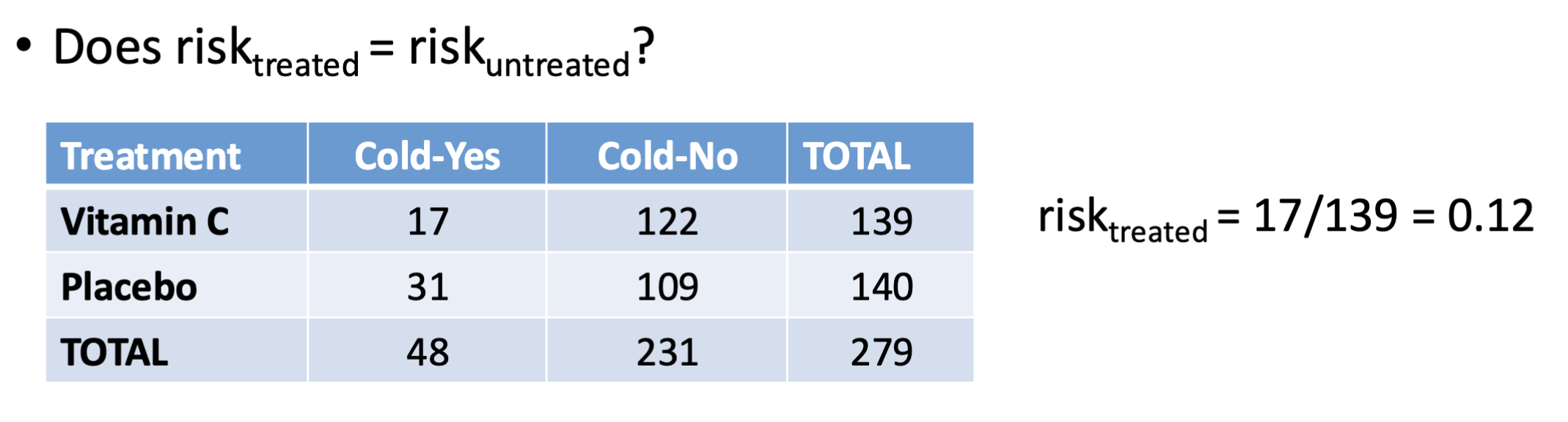
Relative risk formula

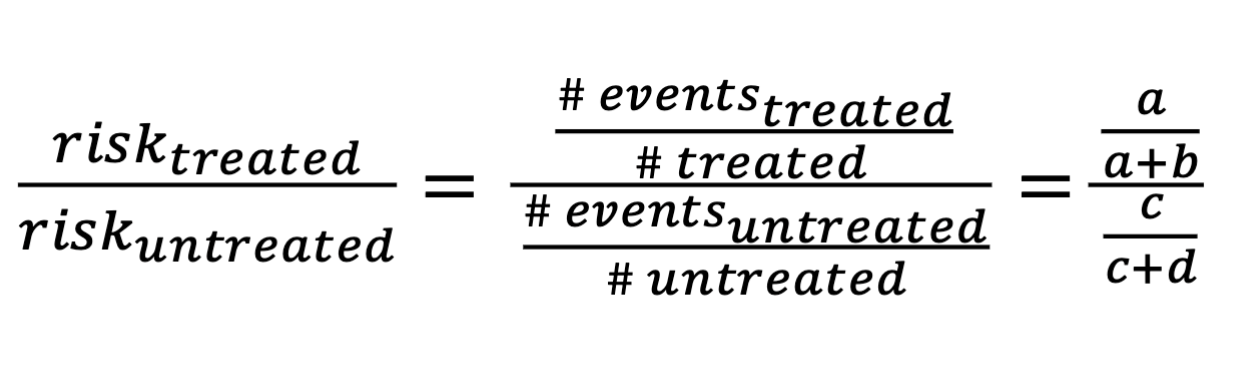
Relative risk table

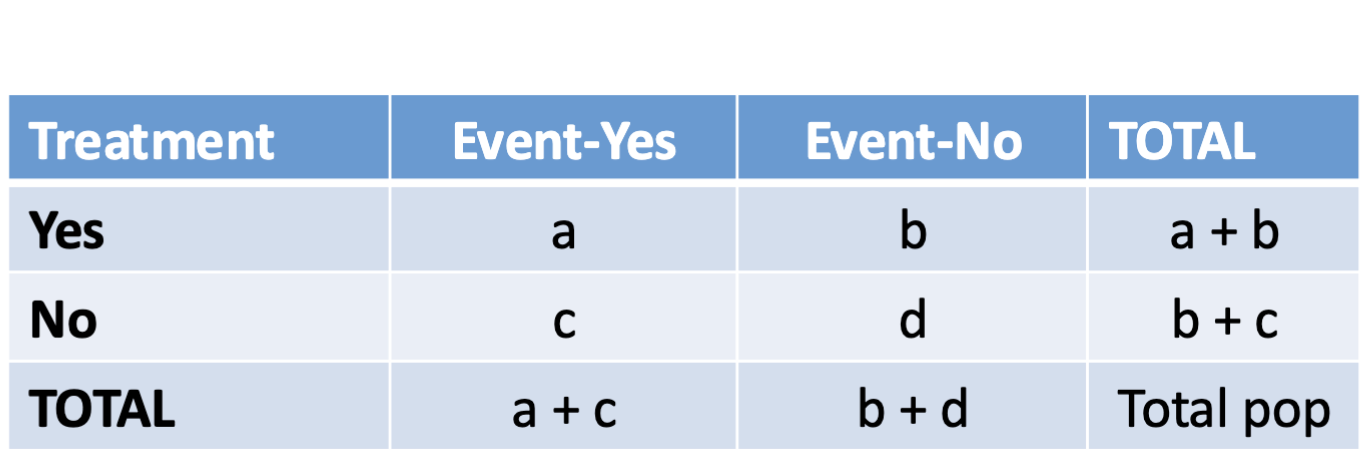
Relative risk is

Risk of treated over risk of untreated, max can be 1

Summary measure of association between risk factor and outcome; 0 <= RR <= infinity

If RR <1

Treatment is associated with lower risk of outcome

If RR > 1

Treatment is associated with higher risk of outcome

If RR = 1

No association of treatment with outcome

Depending on study design, RR may have a

Causal interpretation:

If <1, treatment lowers risk; treatment is beneficial

If RR >1, treatment increases risk

If RR = 1, no effect on outcome

RR = 1.1

10% higher risk

RR = 2.5

150% higher risk

RR = 0.6

40% lower risk

Risk difference formula

Risk treated - risk untreated = (a over a+b), - (c over c+d)

Risk difference, RD

Summary measure of association between risk factor and outcome

__ <= RD <= __

-1, 1

If RD < 0

Treatment is associated with lower risk of outcome