Stat 201: Module 1-2

Inferential Questions

Questions regarding how summaries, patterns, trends or relationships in a data set extend to the wider population

Observation

A quantity or a quality (or a set of these) we collect from a given entity/object

Population

Complete collection of individuals or cases of interest

• the population is fixed

• you don’t have access to all elements of the population

• we mathematically denote the population’s size using upper-case N

Population Parameter

A quantity that summarizes the population

• parameters are constant (not random)

• parameters are usually unknown

Whenever we’re interested in a proportion of some value in a population, the population parameter has a specific name: the population proportion

Census

An exhaustive enumeration or counting of all N individuals in the population

• we do this in order to compute the population parameter’s value exactly

Sample

A collection of observations from a population

Sample estimate

Numerical characteristic of the sample that estimates the population parameter

Statistical Inference

The process of using a sample to make a conclusion about the broader population from which it is taken

Point Estimate (aka Sample Statistic)

Single number calculated from a random sample that estimates an unknown population parameter of interest

• the value is only an estimate (our best guess of our population parameter using this sample)

• since the sample was random, if we took another random sample and compute the value for that sample, we’d get a different answer

• estimates vary from sample to sample due to sampling variability

  • if we get a different value for an estimate w/ a different sample, the point estimate might be unreliable

• specific name when considering proportion: the sample proportion

Variable

An attribute of the elements in the population

• what we’re measuring for each individual

Random Sample

A randomly selected subset of the population

• ensures our point estimates are accurate

• ensures that a sample is unbiased and representative of the population

• every individual has an equal chance of being sampled

• changes every time you draw a sample

• you do have access to all elements of the sample

Sampling

The act of collecting a sample from the population, which we generally do when we can’t perform a census

• we mathematically denote the sample size using lower case n

• typically n is much smaller than the population size

• sampling is a cheaper alternative than performaing a census

Representative Sample

A sample is said to be representative if it roughly “looks like” the population

Generalizable Sample

We say a sample is generalizable if any results based on the sample can generalize to the population

Biased/Unbiased Sampling Procedure

• a sampling procedure is biased if certain individuals in a population have a higher chance of being included in a sample than others

• a sampling procedure is unbiased if every individual in a population has an equal chance of being sampled

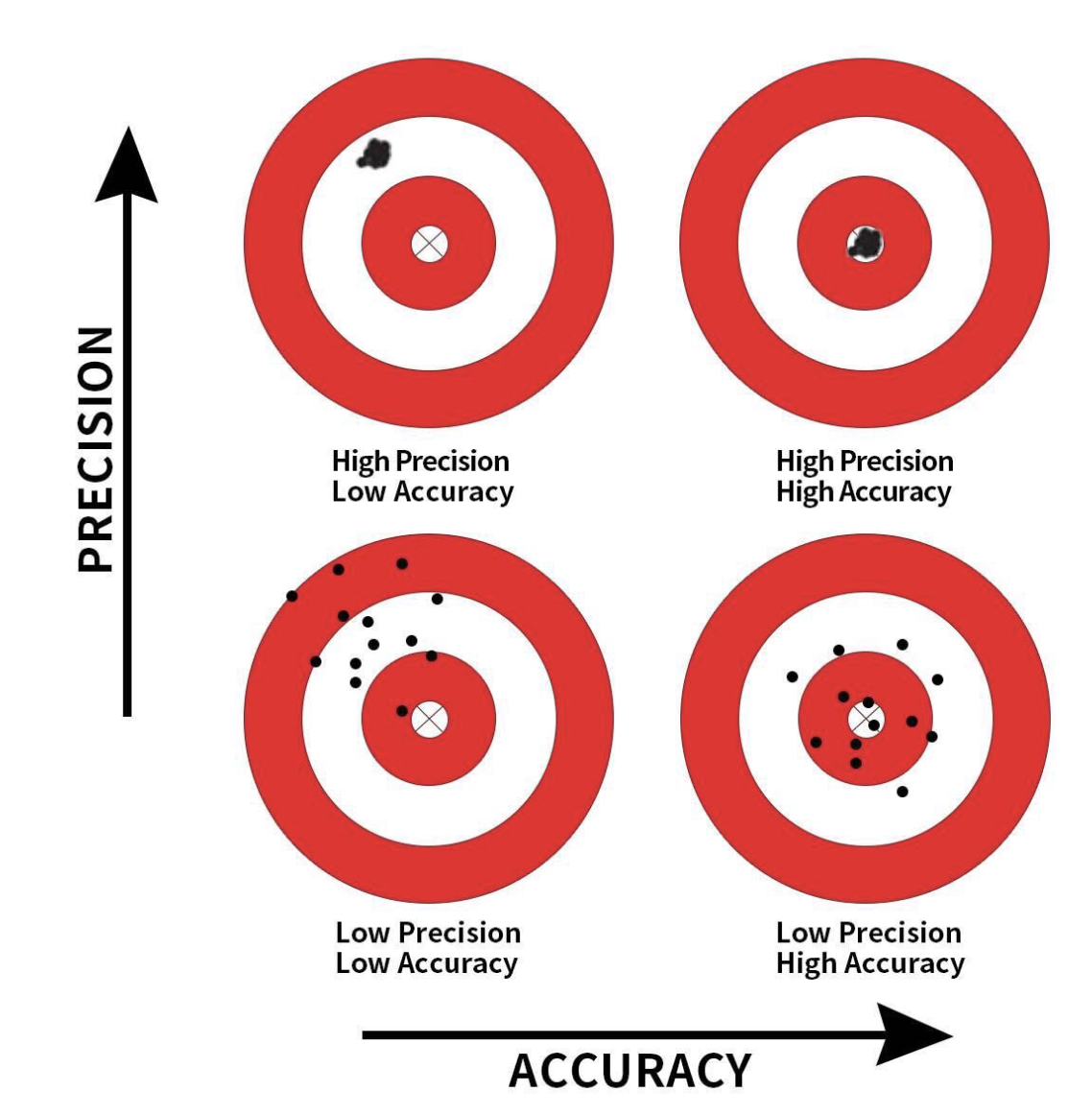
Accuracy vs Precision

• random sampling ensures out point estimates are accurate

• having large sample sizes ensures our point estimates are precise

Statistic

A quantity calculated based on a sample

• eg. sample mean, sample standard deviation

• statistics are used to estimate parameters

• statistics are random quantities and depend on the sample drawn

What happens to the statistics when a new sample is taken?

Statistics will change, since the sample is random. It is likely that the sample will be different every time

Proportion

The number of entities/objects with a specific characteristic divided by the total number of entities/objects

• can be used to describe categorical data

Variance

The mean of the sum of the squared distances of each observation from the mean value of all observations

Quantile

A number such that a given percentage of the data is lower than that number

Correlation

The strength and direction of the relationship between two variables

Sampling Distribution

A probability distribution of a statistic calculated from all possible samples of a specific size drawn from a population

• helps us see how spread out the samples are from each other

• each time we take a random sample we will have the same sampling distribution

• an ideal sampling distribution would be one bar concentrated on the population parameter

• tells us a lot about our statistic

  • we could calculate the probability that our statistic would be to a certain range around the parameter

Sample size on Sampling Distribution

• the bigger the sample size, the more narrow the sampling distribution

  • there are fewer differences due to sampling variation and the distribution centers more tightly around the same value

• the smaller the sample size, the wider the sampling distribution

What does it mean to have a narrower sampling distribution?

• less variability between samples

• the values in the ‘table containing all possible samples' will be closer to the population parameter

  • it matters less which sample is randomly chosen

Questions to consider when looking at a sampling distribution

• what is the centre of the sampling distribution?

• how spread is the sampling distribution?

• what is the shape of the sampling distribution?

What does the sampling distribution show us?

• what point estimates are possible (even more: their probabilities of occurring)

• where the true parameter is (eg. for means it lies at the mean of the sampling distribution)

If we knew the population, could we find the sampling distribution?

Yes, the sampling distribution is usually unknown, but technically if we knew population, you could potentially obtain the exact sampling distribution

• calculate the statistic across all possible samples

• this is only manageable for very tiny problems as there are many possible samples for even small samples

What is the center of a sampling distribution of the sample mean?

The population mean

What affects the variability of the sampling distribution?

• population: affects the samples taken

• sample size

• statistic

Symbols to remember

• Population average = μ

• Sample average = x̄

• Proportion = p

• sample proportion = p̂

Population Distribution

• the population distribution is obtained by measuring all the elements in the population

• the population distribution is unknown

Sample Distribution

• the sample distribution is obtained by measuring all the elements in the sample

• the sample distribution is known

• we hope that the sample distribution resembles the population distribution

Is the mean susceptible to outliers?

Yes, but the median is more robust

Median

The middle observation of a sorted variable’s data

Independence

Independent sample: the selection of one element does not influence the selection of another

Sampling with Replacement

This allows repeated elements in our sample

• works better when the population is larger, as there is a lower chance of getting the same values in a sample, and actually collecting new information

Steps:

1. select one element from the population

2. put the element back in the population

3. do steps 1 and 2 n times

Sampling w/o Replacement

This does not allow repeated elements in our sample

• always getting new information

• more informative than sampling w/ replacement

• impacts independence and the chances of getting chosen

  • when the population is large, the chances of getting chosen aren’t changing as much, but are still not independent

Steps:

1. select one element from the population

2. remove the element from the population

3. do steps 1 and 2 n times

Rule of Thumb: Sample Size

The sample size at most 10% of the population size

Pros of Sampling w/ Replacement

• independent sample: selection of an element doesn’t influence the selection of other elements

• variability even when the sample is the same size as the population

Used for bootstrap samples

Cons of Sampling w/ Replacement

• less informative (repeated information)

• less efficient

Pros of Sampling w/o Replacement

• more informative (less repeated information)

  • more precise parameter estimate

Used for sampling the population

Cons of Sampling w/o Replacement

• Dependence: elements picked affect the chance of the elements you will pick later

  • less problematic when sample is small compared to population

  • need to check 10% rule

• no variability if the sample is the same size as the population

Standard Error (SE)

The standard deviation of a statistic/sampling distribution

• quantifies the amount of variation of the sample statistic around its mean

• general rule, as sample size increases, the standard error decreases

Standard Deviation (σ or s)

The square root of the variance

• measures the amount of variation of the values of a variable about its mean

Surreal Approach to Approximating the Sample Distribution

• taking many samples from the population

  • the approximation depends on the samples we draw

• the more samples that are taken, the more representative they are of the population

Estimating the sampling distribution w/ bootstrapping

• in reality, we only take 1 sample from the population of interest

  • the bigger the sample, the better

• we use the sample distribution as an estimate of the population distribution and take samples w/ replacement from the original sample (bootstrap samples)

• bootstrap samples need to be the same size as the original sample size (smaller = wider bootstrap distribution, larger = narrow bootstrap distribution)

• we then calculate the average in every bootstrap sample and plot the bootstrap distribution to approximate the sampling distribution

• bootstrap samples can’t be used to improve the original sample, we only use it to estimate the sampling distribution

The Bootstrap Distribution

• an approximation of the sampling distribution (has similar spread and shape)

• is centered around the sample statistic (not the parameter)

• used to estimate the standard error of a statistic