5: Dimensional Analysis by Co-Occurrence

Latent Semantic Analysis

A technique of identifying association amongst words in a document - often used for natural language processing.

• Removes the requirement of a square matrix that exists in PCA

• Instead adds the requirement for co-occurrence of events

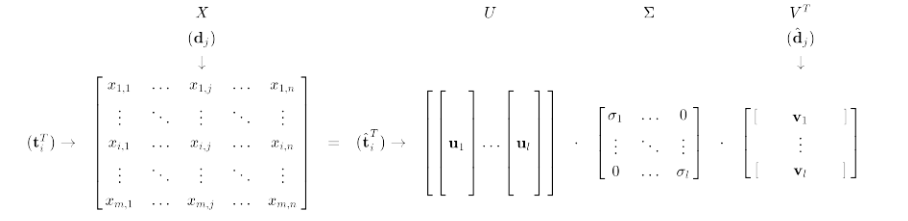
Occurrence Matrix

Describes how frequent different terms happen in each document

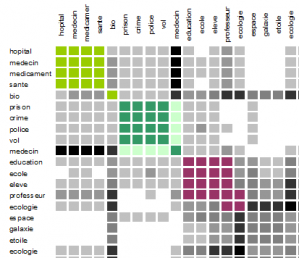
Terms

Events.

Documents

Random variables.

One-Mode Factor Analysis

Every value in the matrix represents the same type of variable (i.e. they’re all co-variances of the variables).

Requirement for covariance to be a good estimator of relations

All variables are unimodal or roughly centred.

Unimodality (of a variable)

There is one single highest value.

Reason to use LSA

It’s another way of looking at relations between variables, specifically co-occurrence of events - central tendency is not generally relevant with multi-model distributions.

Covariance Matrix Format

Where:

• m is the set of random variables

• n is the number of dimensions (rows)

Covariance Matrix - Columns

A vector detailing how relevant the given document (d_j) is to each event.

Covariance Matrix - Rows

A vector corresponding to a term (t_i) and how related it is to each document (random variable).

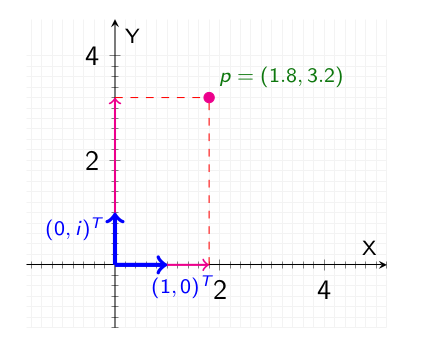
Argand Basis

A coordinate basis used to represent complex numbers.

Complex Conjugate

A number with an imaginary part equal in magnitude but opposite in sign - i.e. z = a + bi and z* = a - bi

Complex Conjugate Properties

• The product of a complex number and its conjugate is a real number: a² + b²

• Conjugation is distributive over four main operations for any two complex numbers.

• Conjugation does not change the modulus of a complex number - |z*| = |z|

• (z*)* = z

• Conjugation is commutative for a power, i.e. (zⁿ)* = (z*)ⁿ

Complex Conjugate Operation - Addition

(z + w)* = z* + w*

Complex Conjugate Operation - Subtraction

(z - w)* = z* - w*

Complex Conjugate Operation - Multiplication

(zw)* = z*w*

Complex Conjugate Operation - Division

(x / w)* = z* / w*, w ≠ 0

Complex Conjugate Application

De-rotation - rotating a vector by 1 + i will rotate it by 45 degrees, which can reversed with 1 - i (the complex conjugate).

Conjugate Transpose Matrix

Transposing a matrix and applying the complex conjugate to each item within.

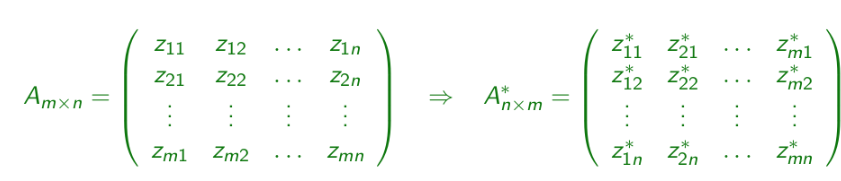
Inverse Matrix

A matrix where AA^-1 = A^-1A = I

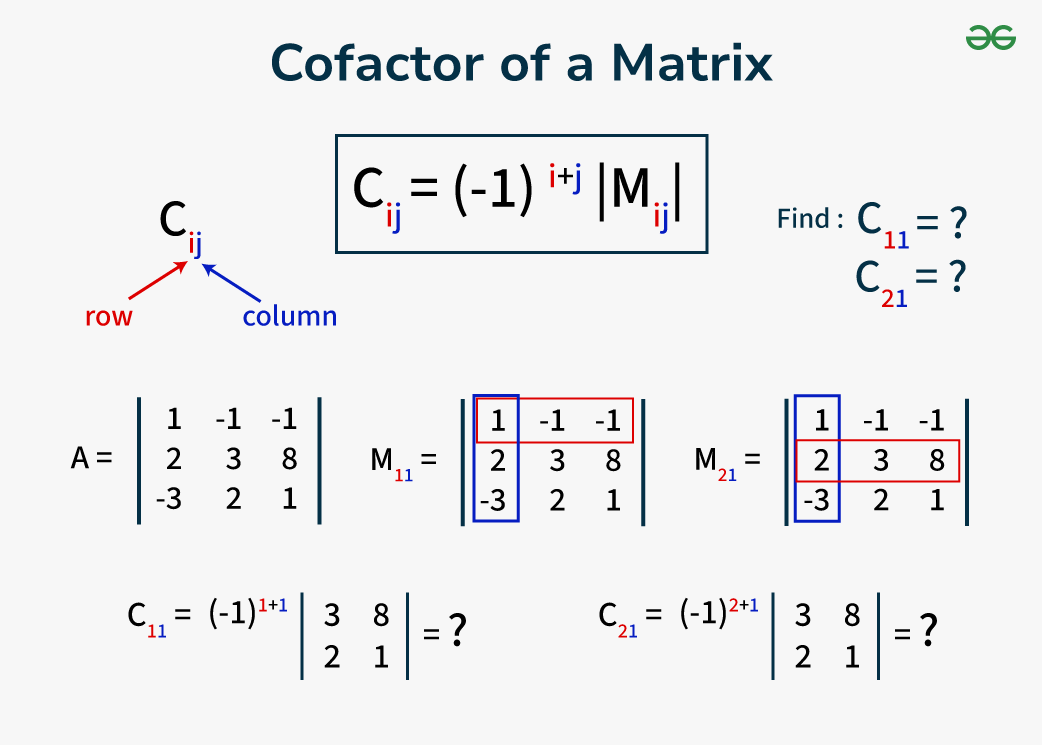
Cofactor Matrix

The minor of an element in a matrix (M_ij) being multiplied by (-1)^i+j.

Adjoint Matrix

The transposed cofactor matrix - adj(A) = cof(A)^T.

Calculating the Inverse Matrix

Calculating the adjoint matrix.

Lanczos Algorithm

An iterative method to find the m “most useful” eigenvalues and eigenvectors of a Hermitian matrix, where m is often but not necessarily much smaller than n.

Lanczos Algorithm - Properties

Efiicient but numerically unstable.

One-Sided Jacobi Algorithm

An iterative algorithm where matrix A is iteratively transformed into a matrix with orthogonal columns: A_new ← A_oldJ(p, q, O) with J(p, q, O) being a rotation matrix.

Two-Sided Jacobi Algorithm

An iterative algorithm that generalises the Jacobi eigenvalue algorithm, where A_new ← J^TG(p, q, O)A_oldJ

• G(p, q, O) is the Givens rotation matrix

• J is the Jacobi rotation matrix

Rank

The number of columns of a matrix.

Latent Semantic Analysis as Singular Value Decomposition