Jointly Distributed Random Variables
0.0(0)
0.0(0)
Card Sorting
1/3
Earn XP
Description and Tags
We can now deal with more than one Random Variable since this is more interesting and more often what we are interested in.
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
4 Terms
1
New cards
What must be established in order to be able to deal with two Random Variables jointly?

2
New cards
Define the Joint Probability Mass Functions
and explain the shorthand
For two Random Variables the values that each one (X, Y) can take is describes by
p(x,y) where p(x,y) = P(X=x, Y=y) intersection of X,Y
and must be legitimate meaning probabilities >= 0 and sum to 1
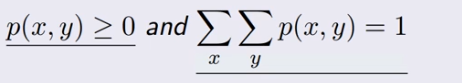
3
New cards
Calculating Probabilities with Joint PMFs
Identifiying the values of X,Y in set A and then which pairs are in A = (x,y) for the given pmf
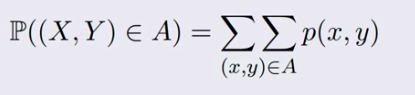
4
New cards
N/A
N/A