Discrete 2 Midterm 3

Graph

A ___ is a non-empty set of vertices and edges connecting vertices. A ____G is with a set of vertices V and edges G, denotes as G(V,E)

where

• V = {V1,V2, V3…Vn}

• E = {e1,e2,e3…en}

End Vertices

2 vertices V1 and V2 are _____ of edge e1.

Parallel

edges that have the same end vertices are _____.

Loop

an edge of the form (V,V) is a ____.

Simple

A graph without any Parallel edges or loop is called ____ .

Empty

A graph with no edges is called ____.

Null

A graph with no vertices is a ____.

Trivial

A graph with only one vertices is ____.

Adjacent

Edges are ____, if they share a common end vertex. 2 vertices U and V are ____, if they’re connected by a edge.

Degree of a Vertex

The ____ written as d(V) is the number of edges with V as an end vertex. By convention; we count loop twice.

Pendant Vertex

A ___ is a vertex with a degree 1.

Isolated Vertex

An ___ is a vertex whose degree is 0.

Pendant Edge

An edge that has a pendant vertex as a end point, is a _____.

Max Degree

The minimum degree of the vertices in a graph G is denotes as S(G) and the _____ denoted as Δ(G).

Handshaking Theorem

In any undirected graph, the sum of the degrees of all the vertices is equal to twice the number of edges.

Imagine a room of people shaking __ :

• Each ___ involves two people

• So if there are 10 , there are 20 _involved

• Similarly, each edge contributes 2 to the total degree count (1 per vertex)

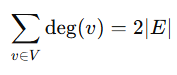
When does Handshaking Theorem not apply:

In a graph with an odd number of vertices with odd degree, the ____ is violated

Subgraph

A graph Gi = (Vi,Ei) is a ____of G (V,E) if:

• V_i ⊆ V

• E_i ⊆ E, and each edge in E_i has the same endpoints in G

• So: A ___ just carves out part of the original graph - it doesn’t modify connections.

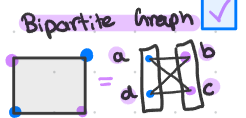
Bipartite Graph

A graph is ____if its vertex set V can be partitioned into 2 disjoint sets V₁ and V₂ such that

1. V = V₁ ∪ V₂

2. Every edge connects a vertex from V₁ to a vertex from V₂

3. So: No edge connects vertices within the same part

4. A graph is _____if and only if it has no odd-length cycle

Complete Bipartite Graph

Denoted by K_m,n

Every vertex in V₁ is connected to every vertex in V₂

Number of edges = m x n

K_3,4 : 3 vertices on left, 4 on right, all cross-connected

Cycle Graph

A graph with n >= 3 vertices, each of degree 2

All vertices form a closed loop

Wheel Graph

Formed by adding a center vertex to a cycle C_n-1

That new vertex connects to all vertices of the cycle.

step 1: take Cx step 2: add a vertex to Cx step 3: connect all vertices

Complementary Graph (or Graph Complement)

The ___ (G with a overline) of a simple graph G has the same vertices as G.

2 vertices are adjacent in (G with a overline) if and only if they are not adjacent in G.

Complete Graph

The __ with n vertices; K is a graph contains all possible edges between every pair of its vertices.

Adjacent paths are different colors means its bipartite graph.

Walk

A sequence of vertices and edges that helps us to travel from initial vertex a vertex to any other vertices (terminal vertex) in a graph (can repeat both)

Trail

A walk with no repeated edges

Path

A walk with no repeated vertices

Closed Walk

A walk that starts and ends at the same vertex

Closed Trail

a _____ that starts and ends at the same vertex - a circuit

Closed Path

a ____ that starts and ends at the same vertex - a cycle

Circuitless Graph

A graph is ___ exactly when there are no loops and there is at most 1 (one) path between any 2 given vertices.

Connected Graph

Every pair of vertices is connected by a path

Disconnected Graph

At least one pain of vertices has no connecting path

Cut Vertex

A vertex whose removal increases the number of connected components

K_n (complete graph) is not bipartite if

n ≥ 3 because it contains triangles (odd cycles)

Cn (cycle graph) is bipartite only if

n is even

A graph is bipartite iff

it has no odd-length cycles

Length of the Walk

The ____ is equal to the total number of edges that you go over

Euler Walk

An ___ is a walk that uses each EDGE exactly once.

Euler Circuit

An ____ is a closed walk that uses each EDGE exactly once.

Euler Graph

A ____ is a connected graph that contains an Euler Circuit

Euler Trail (or Path)

A ___ that visits every EDGE exactly once, but does not need to return to the start

A connected graph has an Euler CIRCUIT iff

all VERTICES have EVEN degree

A connected graph has an Euler TRAIL (but not circuit) iff

exactly 2 VERTICES have ODD degree

Hamiltonian Path

A ___ that visits every VERTEX exactly once (edges may be reused)

Hamiltonian Circuit

A cycle that visits every VERTEX exactly once and returns to the start

Hamiltonian Graph

A graph that contains a hamiltonian circuit

Dirac’s Theorem

If G is a simple graph with n>= 3 vertices, and the degree of every vertex is at least n/2, then G has a Hamiltonian circuit.

Ore’s Theorem

If G is a simple graph with n >= 3 vertices, and for every pair of non-adjacent vertices u and v

deg(u) + deg(v) >= 8

then G has a Hamiltonian circuit

A graph with a pendant vertex (degree 1)

cannot have a Hamiltonian cycle - Because you can only enter and exit a vertex once in a Hamiltonian cycle — and a degree 1 vertex can't support both an entry and an exit.

Tree

A ___ is a connected undirected graph with no simple circuits.

An undirected graph is a tree if and only if

there is unique simple path between any two of its vertices.

Trivial Tree

A ____ is a tree consisting of a single vertex.

Forest

A graph that is circuit-free and not connected. A ____ is a disconnected graph with no cycles.

Rooted Trees

A ____ is a tree in which one vertex has been designed as the root and every edge is away from the root.

Level of a Vertex

The ___ is the number of edges alond the unique path between it and the root.

Height

The ___ of a rooted tree is the maximum level of any vertex of the tree

Children

The ____ of V are all those vertices that are adjacent to V and are one level farther away from the root than V.

Parent

If we is a child of v, then v is called the ____ of w.

Internal Vertices

Vertices that have children are called ____.

Terminal Vertex or Leaf

A vertex without any children is called a _____.

Siblings

Two distinct vertices that are both children of the same parent are called ____.

Ancestor

Given two distinct vertices v and w;

If v lies on a unique path between w and the root, then v is ______ of w and w is a descendant of v.

Descendant

Given two distinct vertices v and w;

If v lies on a unique path between w and the root, then v is ancestor of w and w is a _____ of v.

M-ary Tree

A rooted tree where every internal vertex (i.e., a non-leaf) has at most 𝑚 children.

Example: A binary tree is a 2-ary tree where internal vertices have ≤ 2 children.

Full M-ary Tree

A rooted tree where every internal vertex has exactly m children.

In a full binary tree, each internal node has exactly 2 children.

Decision Tree

A _________ is a rooted tree used to represent a sequence of decisions or tests that lead to different outcomes.

• Each internal vertex represents a decision or test

• Each edge represents the result of that decision

• Each leaf represents a final outcome or classification

Bernoulli Distribution X ~ Bernoulli(p)

a __ has exactly 2 outcomes: success (1) and failure (0)

P(X = 1) = p

P(X = 0) = 1-p = q

mean = u = p

variance = o² = p(1-p)

Binomial Distribution X ~ Bin(n,p)

n independent trials

• each trial has 2 outcomes (success/failure)

• each trial has the same probability of success p

• You’re counting the # of successes

• X = # of successes

• p = probability of success in one trial

• mean = u = np

• variance = o² = np(1-p)

• std dev = \sqrt {np(1-p)}

PMF: Binomial Distribution X ~ Bin(n,p)

Probability Mass Function (PMF)

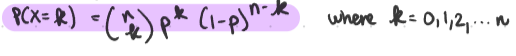
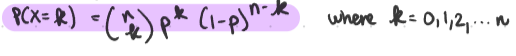
Poisson Distribution X ~ Poisson(k)

when you’re counting the # of events that occur:

• in a fixed interval of time, space, or volume

• where events happen independently

• at a constant average rate

• X = # of events in the interval

• k = mean # of events in the interval

• mean : u = k

• variance : o² = k

• std dev : sqrt k

• k = np

PMF: Poisson Distribution X ~ Poisson(k)

Probability Mass Function (PMF)

Geometric Distribution X ~ Geom(p)

• You’re performing independent trials

• meaning you fail the first k-1 times, then succeed on the kth trial

• each trials has 2 outcomes (success/failure)

• the probability of success is constant (denoted p)

• You’re measuring the # of trials until the first success

• X = 3 of trials until 1st success

  • p = probablity of success on each trial

• mean: u = 1/p

• variance: o² = (1-p)/p²

• std dev: o = sqrt (1-p)/p²

PMF: Geometric Distribution X ~ Geom(p)

Probability Mass Function (PMF)

Hypergeometric Distribution X ~ HG(N,r,n)

• sampling without replacement from a finite population

• population has 2 types (successes in population

• n = # of draws (sample size)

• X = # of successes in sample

• mean and variance is given on the formula sheet

PMF: Hypergeometric Distribution X ~ HG(N,r,n)

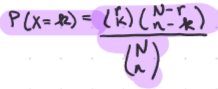
Probability Mass Function (PMF)

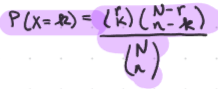
Negative Binomial Distribution X ~ NB(r,p)

• # of trials until the rth success occurs

• like geometric, but not stopping at the first success - stopping at the rth one.

• p = probability of success

• r = target # of success

• X = # of trials until the rth success.

• mean: u = r/p

• variance: o² = r(1-p)/p²

PMF: Negative Binomial Distribution X ~ NB(r,p)

Probability Mass Function (PMF)