Damped Oscillation [Part-I]

Friction, dampen

________ of some sort usually acts to ______ the motion so it dies away, or needs more force to continue.

Car shock absorbers

One example of the case where we have to damp oscillations.

Yes, it is true

Is it true that although we can make friction and other nonconservative forces small or negligible, completely undamped motion is rare.

Damping Oscillation

Oscillation in which the amplitude gradually decreases over time due to a non-conservative damping force that removes energy from the system.

Damping Force

A resistive force that opposes the motion of an oscillating object, typically proportional to its velocity.

b

Symbol that represents the damping constant.

F_D = -b × v

Mathematical Representation of the Damping Force.

That it acts opposite to the motion.

What does the negative sign in the damping force equation indicate?

The amplitude gradually decreases with each oscillation because the damping force from the fluid removes mechanical energy from the system, converting it into heat.

What happens to the spring-mass system when it oscillates in a viscous fluid?

In light damping, the damping force is small, so it removes energy slowly. The restoring force still dominates, keeping the frequency and period nearly unchanged, while only amplitude decays over time.

Why does damping reduce amplitude but not the period (in light damping)?

The viscous drag of the fluid resists motion, creating a force proportional to velocity.

What provides the damping force in a fluid?

Increasing b increases resistance to motion, making the system lose faster, so the amplitude decreases more rapidly and oscillations die out sooner.

What is the effect of increasing the damping constant b?

The total mechanical energy continuously decreases because damping converts kinetic and potential energy into thermal energy in the surrounding medium.

What happens to the total energy of a damped oscillator over time?

ma = -bv - kx

Equation of motion for a Damped Spring-Mass System

Damping constant

A constant that characterizes how strongly the fluid or medium resists motion. Larger b values cause faster decay of amplitude.

Because the weight only shifts the equilibrium position. The restoring force and damping behavior depend on displacement and velocity, not on the absolute weight of the object.

Why does the weight of the mass not affect the period of oscillation?

The system undergoes underdamped oscillations. It continues to oscillate about the equilibrium position with a gradually decreasing amplitude.

What type of motion occurs if damping is very small?

The system becomes over-damped. It returns to equilibrium slowly without oscillating.

What happens if damping is extremely large?

Critical damping occurs when the damping constant is just large enough for the system to return to equilibrium as quickly as possible without overshooting.

What condition produces critical damping?

Damping introduces a non-conservative force, meaning mechanical energy is not conserved; it is continuously lost to friction or fluid resistance as heat.

How does damping affect energy conservation?

m(((d^2)(x))/dt^2) + b(dx/dt) + kx = 0

Equation of motion for a Damped Spring-Mass System (in a differential equation form)

+A_0

(1)

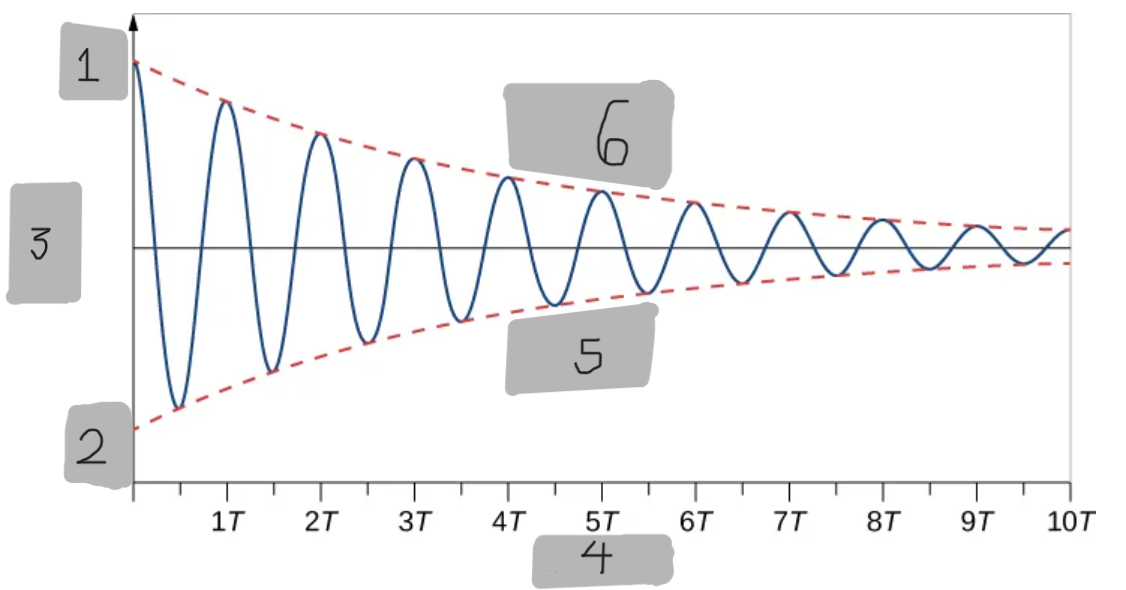
-A_0

(2)

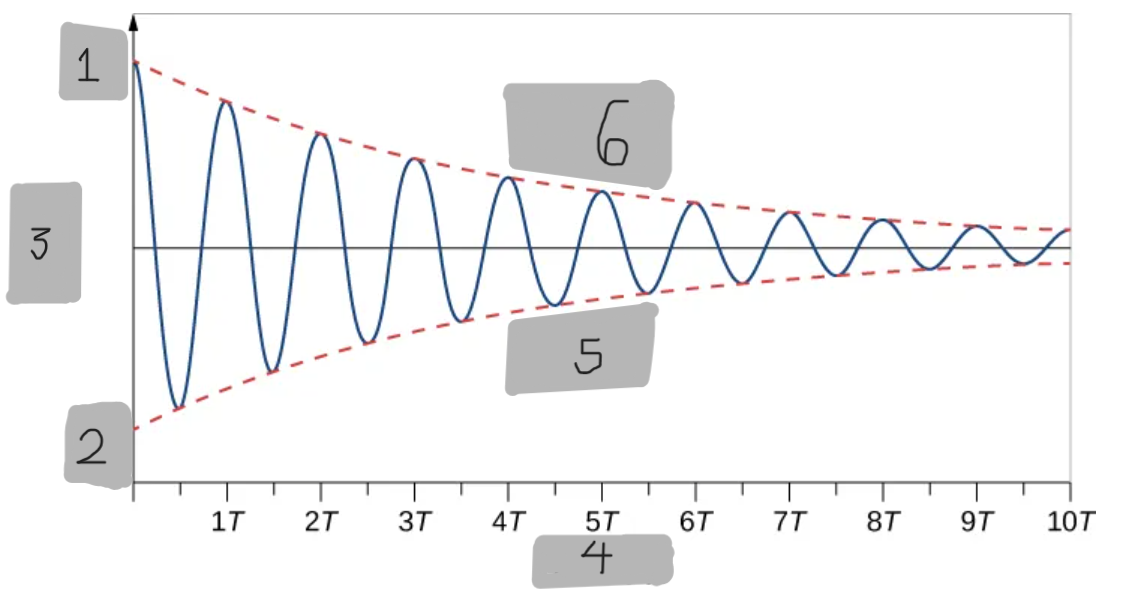
x(m)

(3)

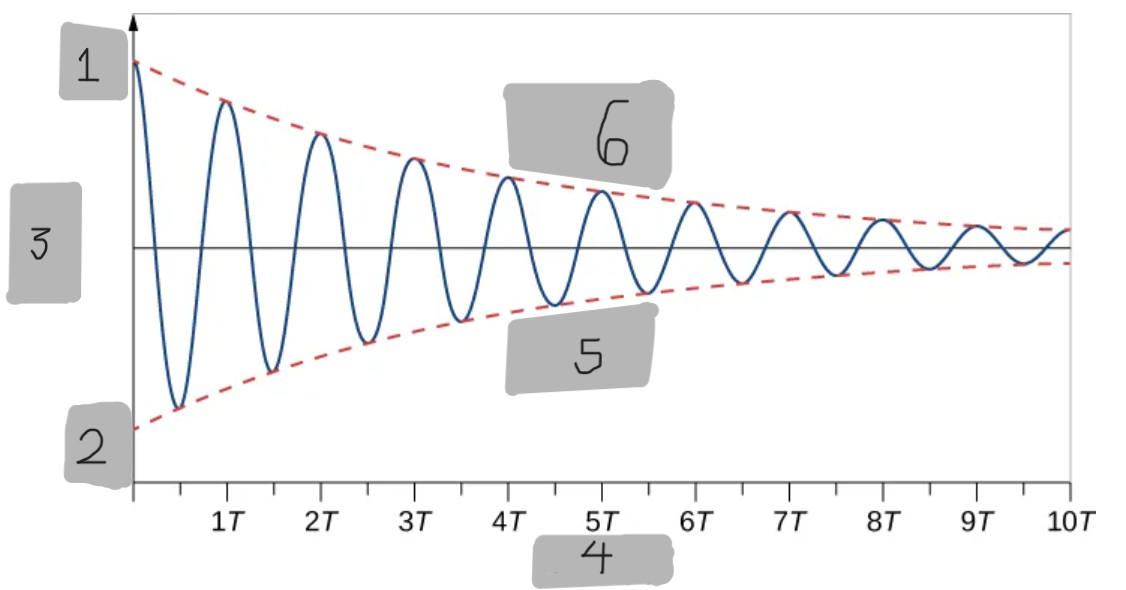
Time(s)

(4)

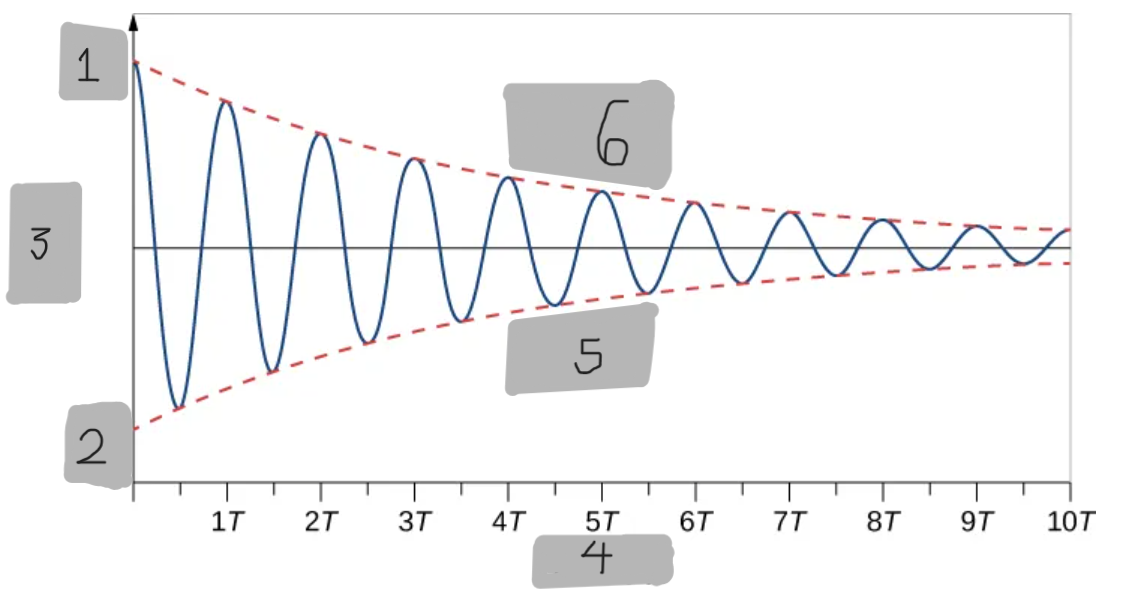
-(A_0)e^(-(b/(2m))t)

(5)

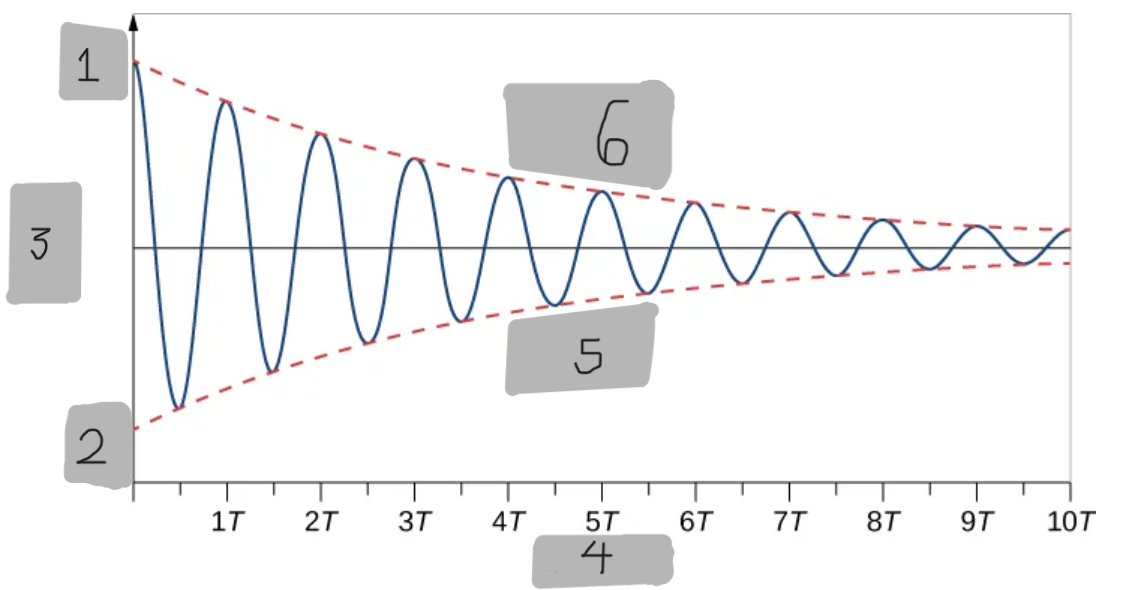
+(A_0)e^(-(b/(2m))t)

(6)

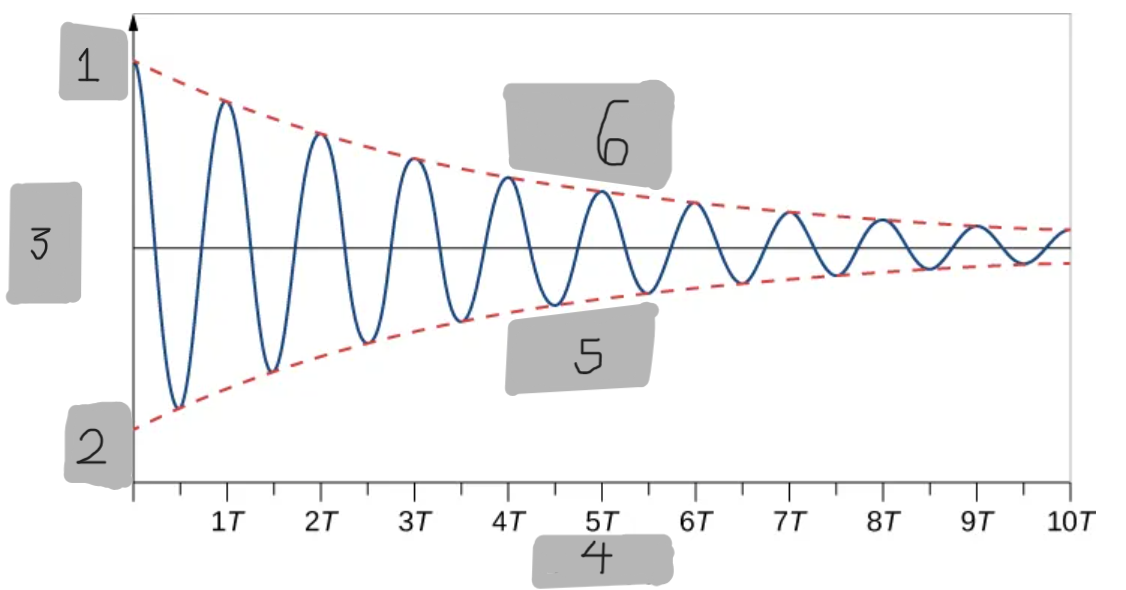
(A_0)e^(-αt)

The exponential function that envelopes the #1 oscillating function graph.

α = b/(2m)

Equation of α

x(t) = (A_0)(e^(-(b/(2m))t))cos(ωt + Φ)

The function to get the provided #1 graph on Desmos

ω = ((k/m) - (b/(2m))^2)^1/2

To prove that #1 is the right solution, take the first and second derivatives with respect to time and substitute into the differential equation. It is found that we will get that right desmos function only if…

Natural angular frequency

The angular frequency of a mass undergoing SHM is equal to the square root of the force constant divided by the mass.

ω_0 = (k/m)^1/2

Mathematical representation of the natural angular frequency

ω = ((ω_0)^2 - (b/(2m))^2)^1/2

Formula for the angular frequency for damped harmonic motion

Cosine function

The #1 desmos function’s curve oscillation is what type of function?