AP Calculus AB Unit 0 Review

The Parent Functions, Algebra 2, Precalculus

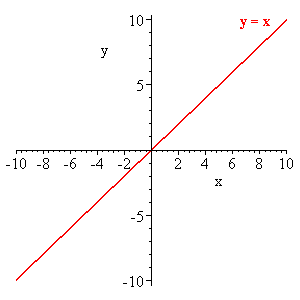
f(x)=x

Odd

Origin symmetry

The parent function of all lines but vertical ones

Reference Points: (-1,-1), (0,0), (1,1)

Domain D : (-∞,∞)

Range R:(-∞,∞)

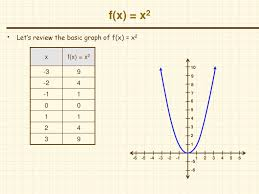
f(x)=x²

even

y-axis symmetry

The even parent function

No negative numbers (zero is non-negative)

Reference Points: (-1,1), (0,0), (1,1)

Domain D: (-∞,∞)

Range R: [0,∞)

For f(x)=x², f(x-a)+b where the vertex is moved to the right a units and moves up b units

Even Function

Definition: f(-x)= f(x)

Characteristic: y-axis symmetry

Parent Function: x²

Have the same end behavior on both sides

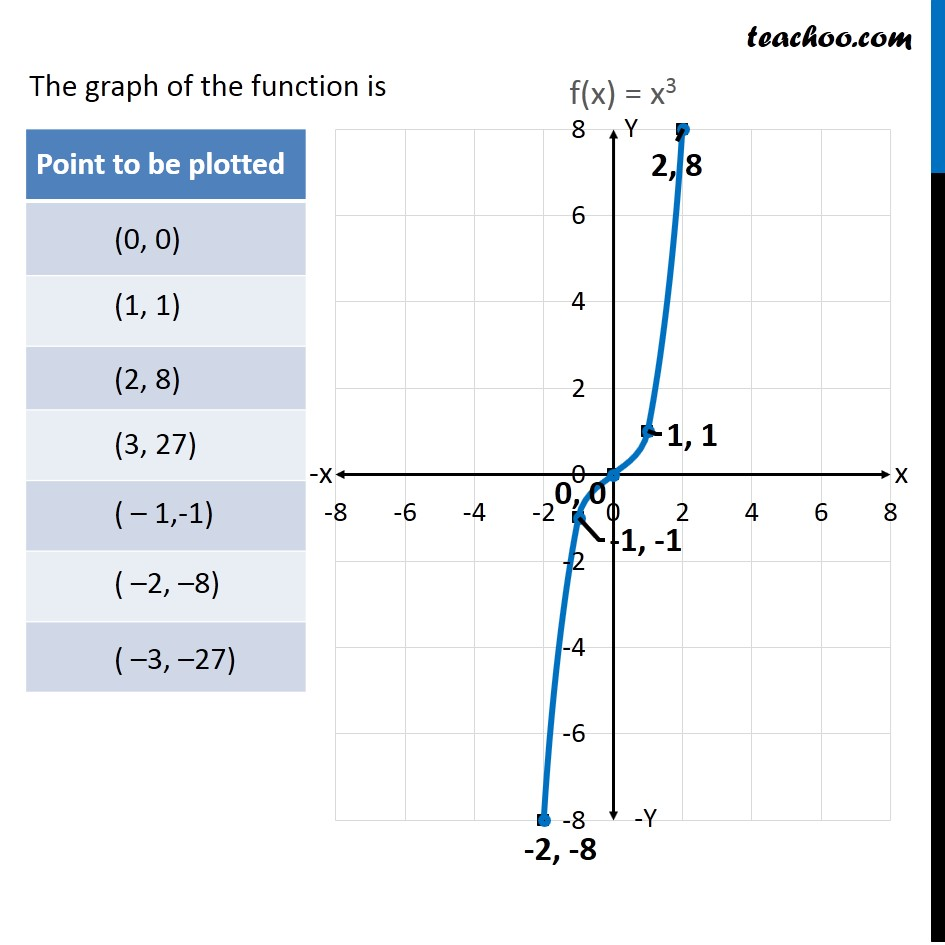
f(x)=x³

Odd

Origin Symmetry

Bends/curve due to being raised to an odd power

Flips at (0,0) and concavity flips to going up

Reference Points: (-1,-1), (0,0), (1,1)

Appears flatter between -1 and 1

Domain D: (-∞,∞)

Range R: (-∞,∞)

Odd Function

Definition: f(-x)=-f(x)

Characteristic: Origin Symmetry (“Odd“=Origin)

Ex: y=x³

Both Function

Ex: y=0

Both even and odd

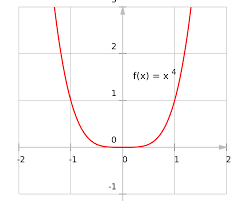
f(x)=x^4

even

y-axis symmetry

Reference Points: (-1,1), (0,0), (1,1)

Also flattens between -1 and 1 and gets more narrow than x² after because it grows faster (almost becomes vertical lines)

It is closer to the x-axis because numbers between 1 and -1 get smaller when you square (multiply it

Domain D: (-∞,∞)

Range R: [0,∞)

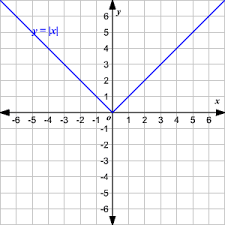
f(x)=|x|

even

y-axis symmetry

Pointy is bad in Calculus (you can’t take the derivative of it!)

Reference Points: (-1,1), (0,0), (1,1)

Domain D: (-∞,∞)

Range R: [0,∞)

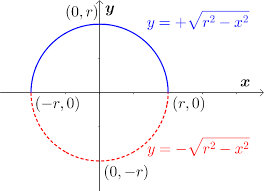
f(x)=√(r²-x²)

Top half of a circle/semicircle

Even

y-axis symmetry

Reference Points: (r,0), (-r,0), (0,r)

Domain D: [-r,r]

Range R: [0,r]

f(x)=1/x

Odd

Origin symmetry

The parent rational function

Reference Points: (1,1), (-1,-1)

Gets pulled as it approaches [-1,1]

Domain D: (-∞,0)∪(0,∞)

Range R: (-∞,0)∪(0,∞)

VA: x=0

HA: y=0

f(x)=1/|x|=|1/x|

Even

y-axis symmetry

Reference points: (1,1), (-1,1)

D: (-∞,0)∪(0,∞)

R: (0,∞)

Reflects anything under the x-axis

Ex: |x²-9|

Pretend the absolute value is not there then flip the negatives over the x-axis

Derivative is undefined at -3 and 3 because it is pointy

Still even if you move up or down

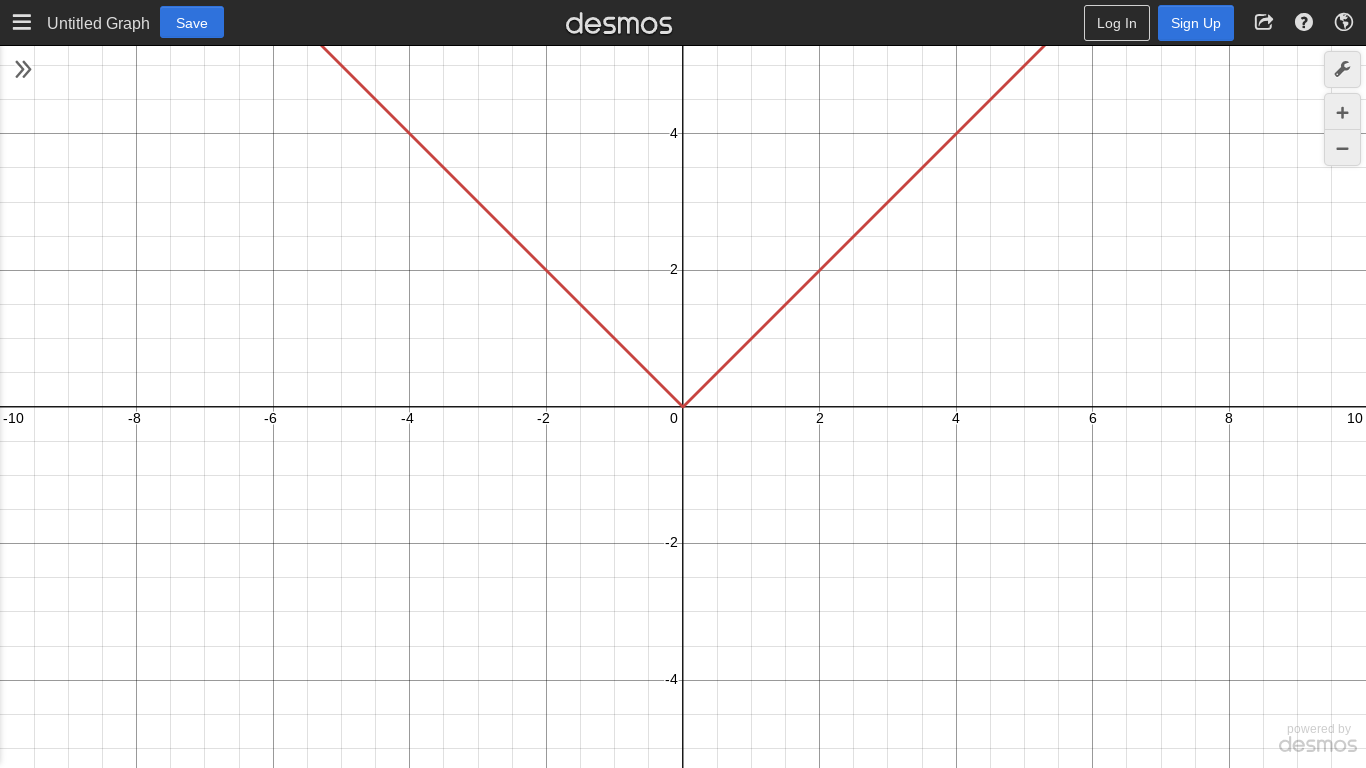
f(x)=1/(x²)

Even (squared)

y-axis symmetry

Reference Points: (1,1), (-1,1)

D: (-∞,0)∪(0,∞)

R: (0,∞)

Approaches x-axis more quickly

Flips the 1/x negative side to the positive because squared on the same axis as |1/x|, further away from the y-axis (approaches VA at slower rate (less powerful) and grows faster)

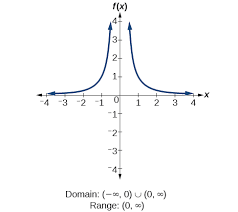
f(x)=1/(x³)

Odd

Origin symmetry

Reference Points: (1,1), (-1,-1)

D: (-∞,0)∪(0,∞)

R: (-∞,0)∪(0,∞)

Approaches x-axis/HA even more quickly and grows faster, approaching y=0 VA even slower

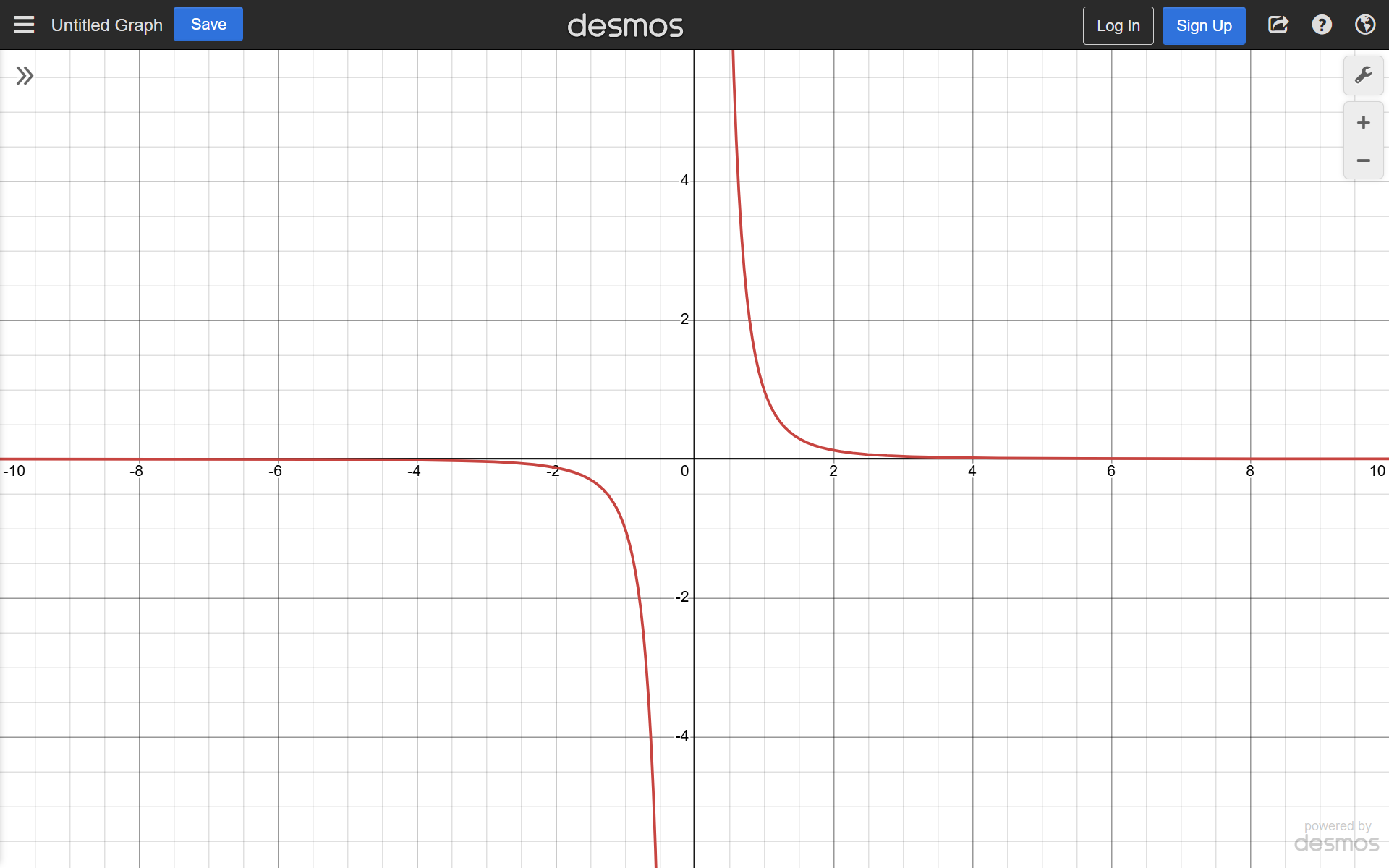
f(x)=√x

Neither even nor odd

Reference Points: (0,0), (1,1)

D: [0,∞)

R: [0,∞)

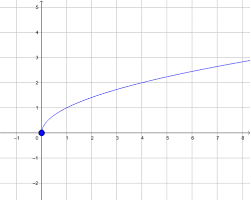
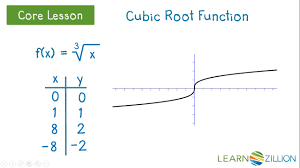
f(x)=∛x

Odd

Not still odd if you move up or down

Reference Points: (0,0), (1,1)

D: (-∞,∞)

R: (-∞,∞)

Slightly flatter than √x, √x is bigger slightly than ∛x

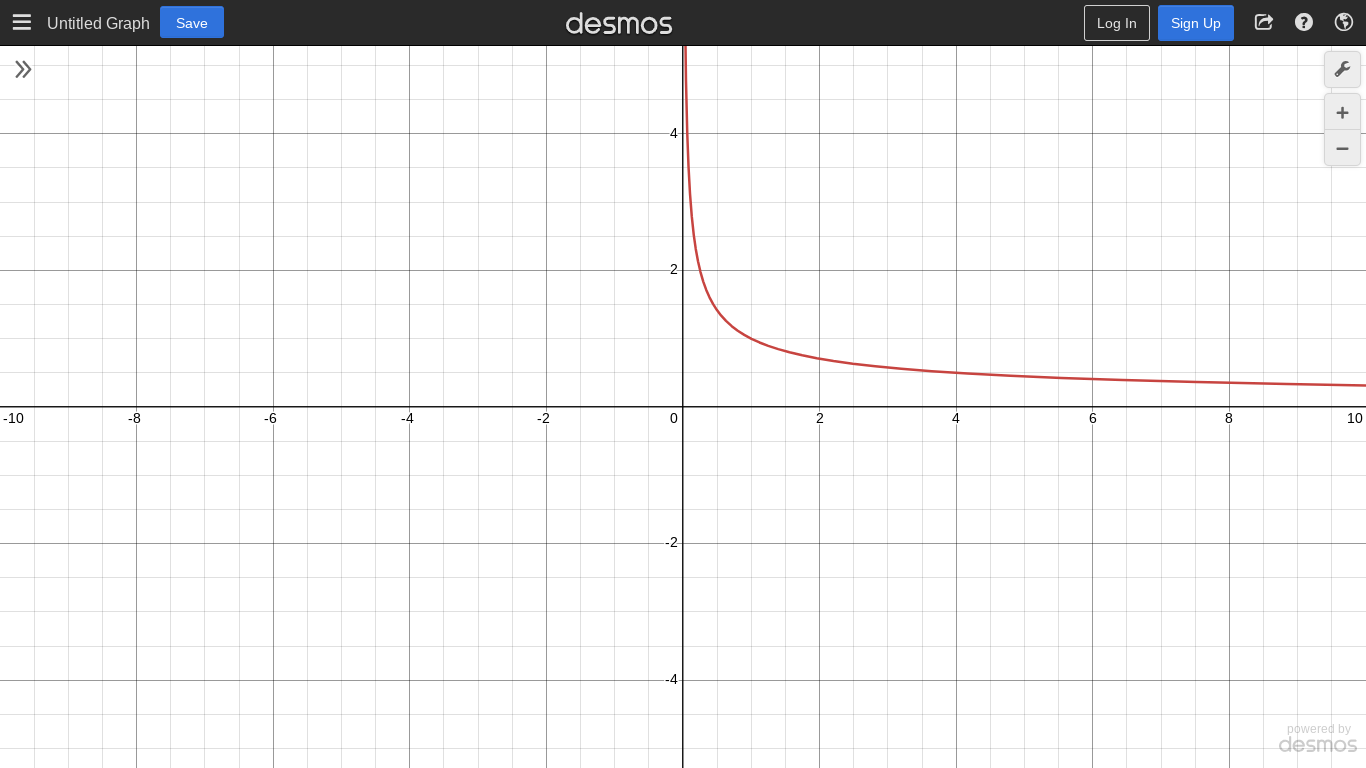
f(x)=1/(√x)

Neither even nor odd

Reference Points: (1,1), (4,0.5)

D:(0,∞)

R: (0,∞)

1/(∛x)

Odd

Reference Points: (1,1), (-1,-1)

D: (-∞,0)U(0,∞)

R: (-∞,0)U(0,∞)

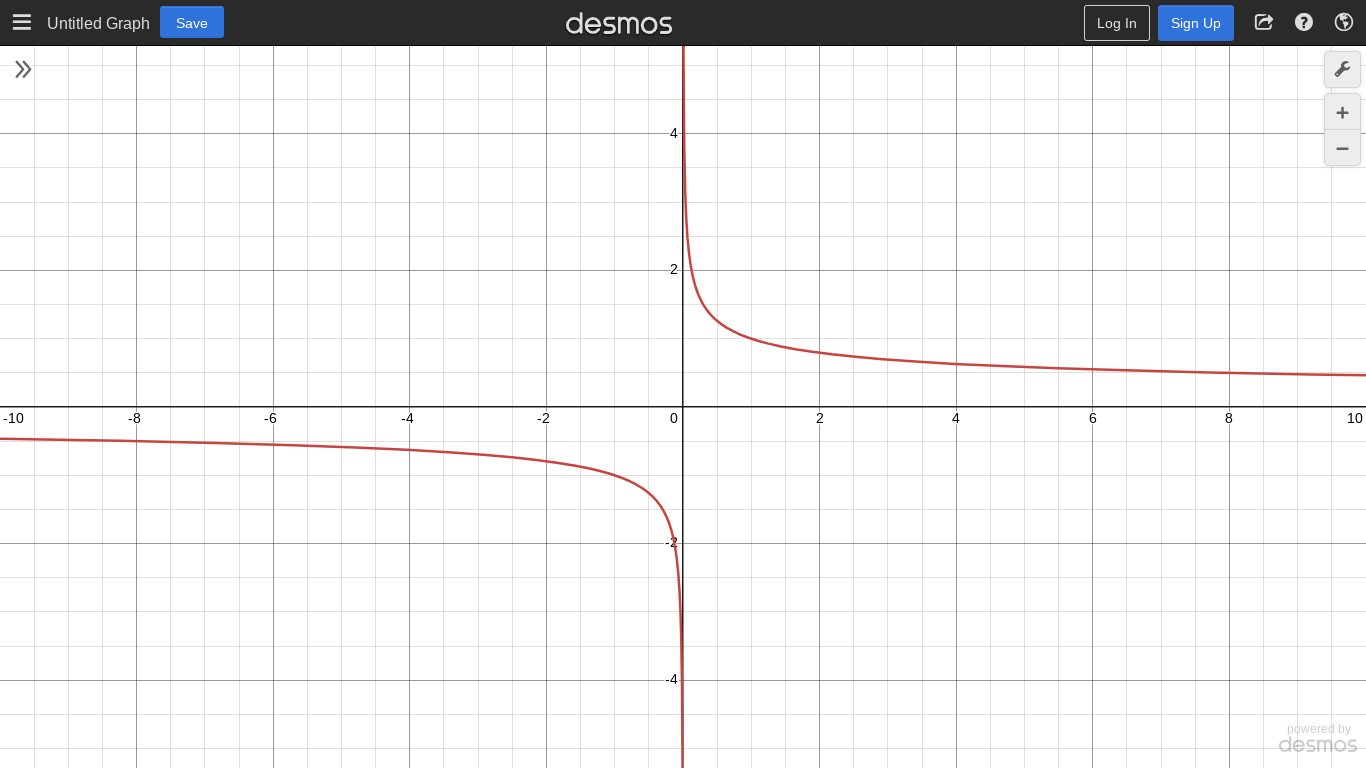
f(x)=e^x

Even

Reference Points: (0,1)

Domain: (-∞,∞)

Range: (0,∞)

y=e^-x flips over the y-axis and becomes exponential decay

y=lnx is the inverse

One-to-one function

y=e^x and y=lnx are symmetric

ass the verticals & horizontal line test

f(x)=lnx

Even

Reference Points: (1,0)

D: [0,∞)

R: (-∞,∞)

Ex: 2lnx grows faster

f(x)=e^x is its inverse

f(x)=sinx

Odd

Reference Points: (0,0), (π/2,1), (π,0), (3π/2,-1)

D: (-∞,∞)

R: (-1,1)

If f(x)=sinx, f(-x)=-sinx. f(-x)=-x so f(x)=xsinx so f(-x)=(-x)(sinx)=xsinx.

f(-x)=even

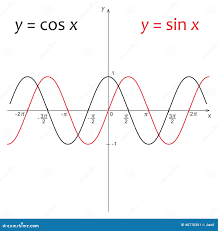
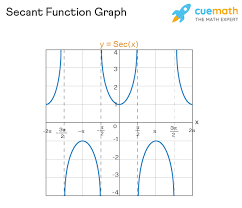
f(x)=sec x

even

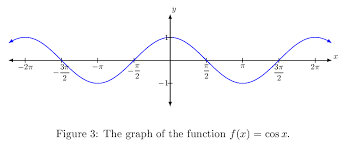
f(x)=cosx

Even

Reference Points: (0,1), (π/2,0), (π,-1), (3π/2,0)

D: (-∞,∞)

R: (-1,1)

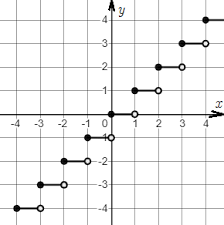
Greatest Integer Function (f(x)=⌊x⌋)

The greatest integer function assigns to each number the greatest integer less than or equal to the number. If we denote the greatest in x by ⌊x⌋ (sometimes called the floor of x), then we have ⌊5.28⌋=5, ⌊5⌋=5, ⌊π⌋=3, ⌊-1.7⌋=-2

*f(x)=⌈x⌉ is the least integer function (ceiling of x) and assigns to each number the least integer greater than or equal to the number)

Difference Quoticent

DQ = f(x+h) - f(x) / h

Rationalise the Numerator by multiplying by the denominator

{} in Calculus

Means order does not matter

ie. {x|-4<=x<x<10}={x:-4<=x<x<10} means “the set of all xs such that“

[ ] and () in Calculus

means order does matter

Numbers in Calculus

Always in reals numbers in this class

NO IMAGINARY NUMBERS

Points in this Class

Calculus can only be done on CONTINUOUS DATA not points

Graph Direction

Never go from right to left on graphs

Definitions in Calculus

You HAVE to KNOW DEFINITIONS to justify

x>0 sign

is not POSITIVE but NON-NEGATIVE

Wording on AP Exam

EVERY SINGLE WORD matters to the problem on the AP exam

|x|=

{ x, x>0

{ -x, x<0

|x|=10, b ∈ℝ → x=±b

|x|<10 → -10< xb

|x|>10 → 10 <x, x< -b

Absolute value in Calculus

You cannot do Calculus on Absolute Value & must use PIECEWISE FUNCTIONS

Circles in Calculus

Cannot do Calculus on circle (non-function)

Standard Form of a Circle

x²+y²+Cx+By+C=0

(x-h)²+(y-k)²=r²

This makes a circle

Number of roots of a Polynomial (Fundamental Theorem of Algebra)

If f(x) is a polynomial of degree n>0 and f(a)=0, then (x-a) is a factor of f(x) and f(x)/(x-a) is a polynomial of degree n-1. So repeatedly applying the FToA, we find that f(x) has exactly n complex zeroes counting multiplicity.

Ex: x³-9x=0 has either 3 real roots or 1 & 2 imaginary (non-real complex roots come in conjugate pairs, so there cannot be 2 real & 1 imaginary)

Equation of half of a circle

Top half: y= +√(r²-x²)

Bottom half: y= -√(r²-x²)

Centre (0,0)

Commutative Property

Ex: 4^x=(2²)^x=(2^x)²

Square Root Property

If b∈ℝ (elememt of the reals) and x²=b, then x±√b

Conic Sections in Calculus

The conic sections in calculus are mainly ellipses and parabolas

Number Line

A number is smaller than another if it is left of it on the number line

Undefined and Does Not Exist

There is a difference between undefined and “does not exist“

Rationalising Denominators in Calculus

No need to rationalise denominators

Vertical Line

x=C

Slope undefined

Horizontal Line

y=C

0 Slope

Derivative

Derivative is the slope of a straight line

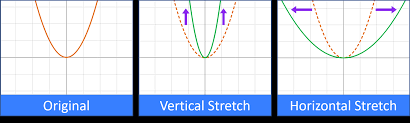
Vertical Stretch

Growing faster= vertically stretch= grows more narrow

Vertical Compression

Growing slower= vertical compression= grows more wide

cos(0)

1

Amplitude of Function

Impacts Range

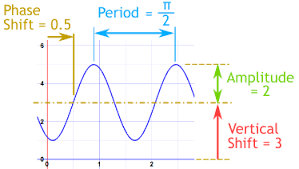
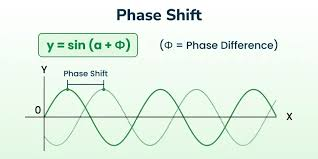
Phase Shift of Function

Translates Φ units to the left

Numerical

Data

Inverse Function

f(g(x))=g(f(x))

f(x) and g(x) are inverses if f and g composed can only be x

Ex: f(x)=√x, g(x)=x²

f(g(x))=√x²=|x|

g(f(x))= (√x²)=x

Inequalities in Range

Ex: 0<y<∞

y gets closed to but never = 0 & is positive

Difference Quotient Characteristics

(f(x+h)-f(x))/h (USE PARENTHESIS)

1. In a difference quotient, everything without Xs cancels

2. Everything remaining should have an h & therefore something should cancel

Exponent only acts upon its base

Ex: Exponent only acts upon its base, which is e and not 6 because of no parenthesis in 6e^(2ln4+3)=6(e^2ln4)(e³)

Rational Functions

Polynomial/Polynomial

If f(x)= (p(x))/(q(x)), p(x) & q(x) are polynomials, then it is a rational function

D: (-∞,∞), q(x)=/=0

Have either a horizontal or an oblique asymptote

Horizontal asymptotes in rational functions have to do with the degree in the numerator and denominator

• degree (denominator)> degree (numerator) (very small number close to zero when you plug things in) so y=0

No x-intercept

Ex: f(x)=(-30)/(x²+2) where the bottom is always positive and -30 cannot be set equal to 0. There are only negatives in the range, and -30/(x²+2)=anything but 0

No vertical Asymptotes

The denominator isn’t 0

Vertical Asymptotes

Are much stronger than horizontal, as they can allow variation up to one time

Asymptote

Asymptotes pull the (act as magnets) functions towards them

Number of y-intercepts of Function

Only 1 y-intercept because a function passes the vertical line test

Limits at Finite Numbers

When approaching a finite number as opposed to ∞ or -∞, as x →z (#) y→w (#)

Average Rate of Change

Slope of secant line (a,f(a)) and (b, f(b)) is the average rate of change over [a,b]

Rounding in Calculus

Round to 3 decimals even in intermediate steps, or truncate

Be Able to Find

1. Zeroes of functions

2. Zeroes of curves

3. Points of intersection

4. Take a numerical derivative

5. Numerical integral

Zoom Standard

[-10,10]X[-10,10]

(with -10 being the x and y-min and 10 being the x and y-max)

Trace

Trace step is trash