Section 4 - Operational Amplifiers

Operational Amplifiers Picture

lever-shifter, buffers, comparators, adders, subtractors, integrators, differentiators, current source

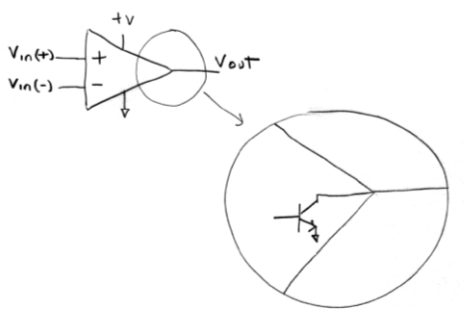
Properties of Ideal Op Amp

input infinite impedance (Zin = infinity → no current) and 0 output impedance (Zout = 0); infinite gain (|Vout/Vin|)

Infinite Input Impedance

reads input V w/o changing it by drawing current

0 Output Impedance

can provide infinite output current w/o affecting V; Vout = V - IR = V

Infinite Gain

= for both inputs so can have single variable A; Vout = A(Vin+ - Vin-), A → infinity

Comparator

single Op amp for comparing V; has a single-sided power supply (+ and ground); open collector output → sink/pull I not source it; no R or C; fast, simple, and digital; open collector output

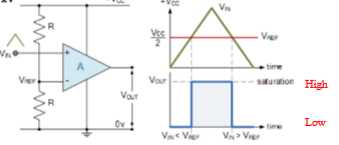
0 Crossing Detector

a comparator circuit that compares input V to reference (0 V when grounded); crossses 0 (either - → + or + → -); high state (Vin > Vref → + saturation of output) or low state (Vin < Vref → - saturation of output)

Comparators: offset reference voltage

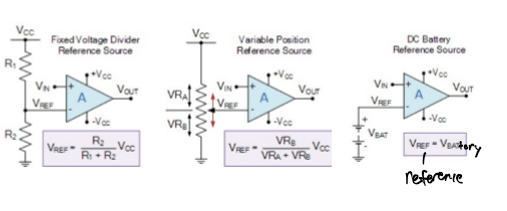
+ Voltage Comparator - Noninverting

Vin > Vref → output will saturate towards + supply rail, Vcc

Vin < Vref → output will change state and saturate at - supply rail, 0 V

Vref = ½ * Vcc

Negative Voltage Comparator - Inverting

Vin < Vref → output will saturate towards + supply rail, Vcc

Vin > Vref → output will change state and saturate towards - supply rail, 0 V

Oscillator

capacitor charges/discharges between 2 thresholds; basically thermoregulator but with a capacitor as “memory” instead of heat

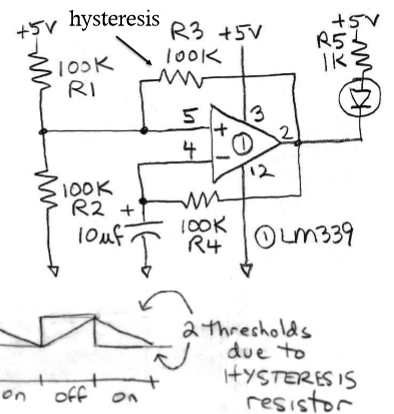
What can a comparator power?

a relay

Advantages of a Comparator powering a relay

switch provides 0 → infinite resistance and up to 1 A; isolation between coil and switch; diode needs to protect comparator from surge in coil; COMPARATOR PROVIDES INFINITE INPUT IMPEDANCE

Comparator vs Op Amp

comparator - output digital/binary; faster; open collector output; usually just + power and ground lowest V

op amp - output analog (basic for linear systems w/ gain); slower; push-pull output (sink or source I → NPN and PNP transistors); has ± power supplies w/ ground in middle

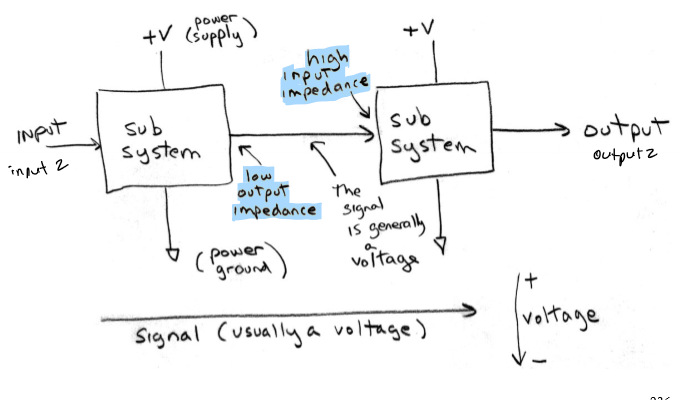
Operational Amplifier

Vout = A (Vin+ - Vin-), A → infiinity; infinite input impedance, 0 output impedance, inifinite gain; 2 input terminals but 1 output hat amplifies difference between inputs; has AC and DC componenets so frequency = 0

Voltage Follower/Buffer

± inputs equal; 0 input I and large output I; has - feedback; gain is infinite (A = Vout / (Vin - Vout) ); V gain of 1; adds high input impedance so little I drawn

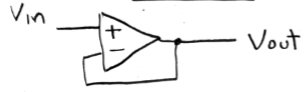
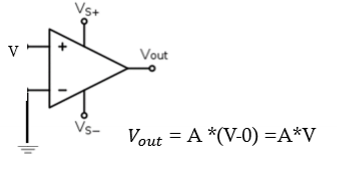
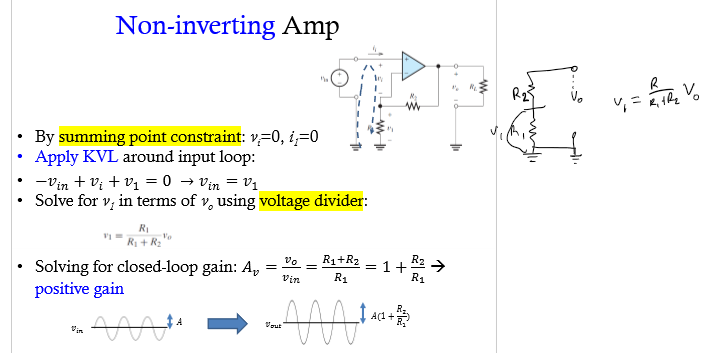
Non-inverting Op Amp

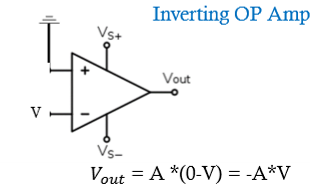
Inverting OP Amp

+ becomes - and - becomes +; sin becomes cos and cos to sin; R2 is feedback R with - feedback; has the summing point constraint

OP Amp - Operational Response

can not have more than supply V; Vout = A * Vd; slope is gain

Summing Point Constraint

differential input V and I are forced to 0; when both grounded inputs are grounded

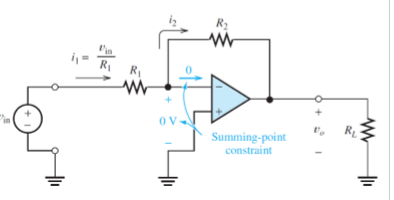
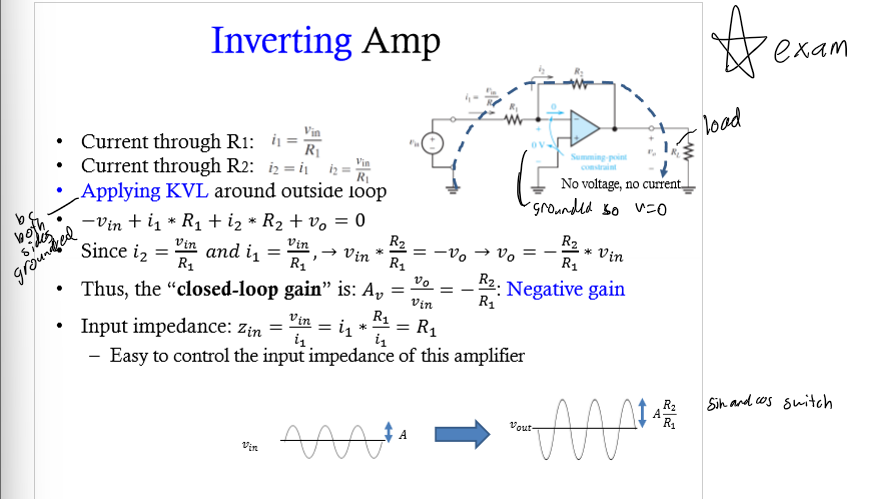
Inverting Amp Example

Non-inverting Amp Example

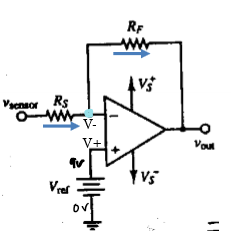
Lever Shifter

remove DC component from Op Amp; use KCL; bc of summing point constraint know that V- = V+ = Vref; by adding Vref DC component of the signal is removed at the output → shifts the level of the signal

Vout = - Rf/Rs * delta Vsensor

Vsensor = Vo(DC) + deltaVsensor (AC) (measured by adding Vref)

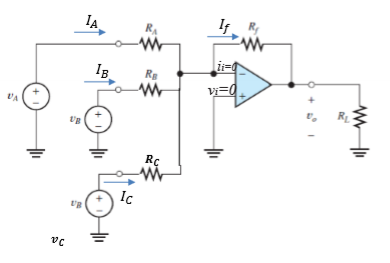
Adder

V at inverting input is 0 (from summing point constraint); apply KCL, KVL, and Ohm’s Law; find eqns. using summing point constraints; V eq. around loop

OP Amps w/ Complex Impedance

math the same but replace R with Z

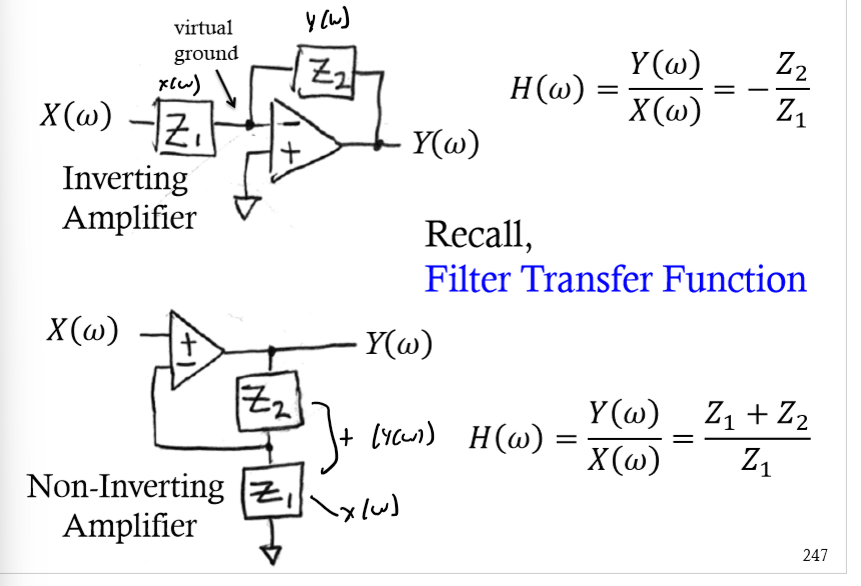
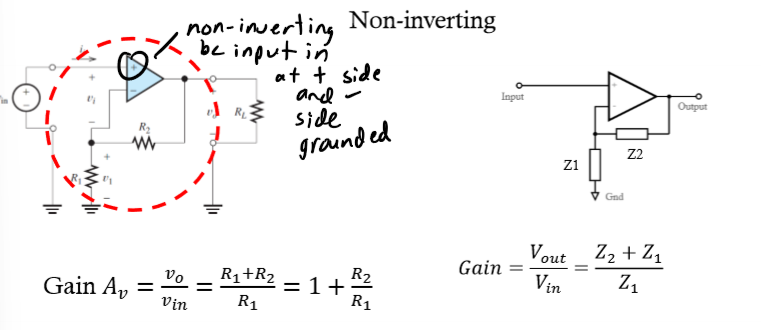
Complex Impedance - Non-inverting

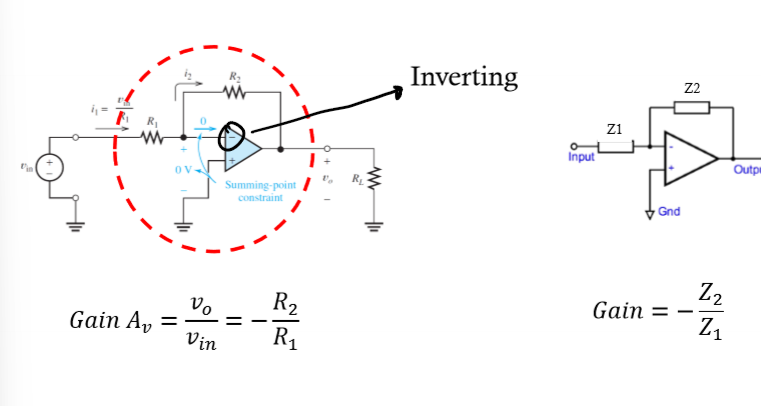
Complex Impedance - Inverting

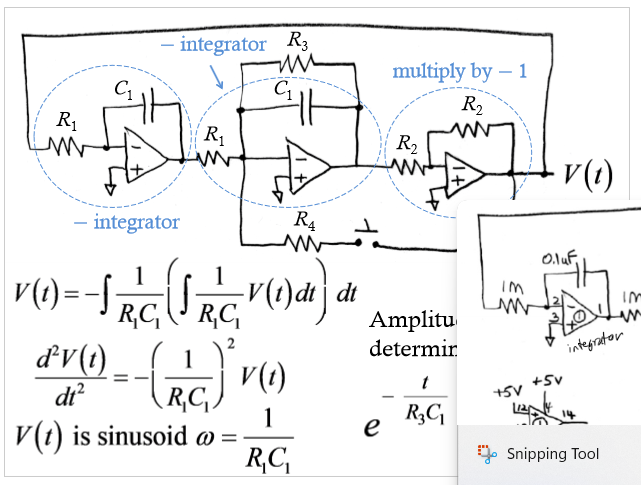
Integrator

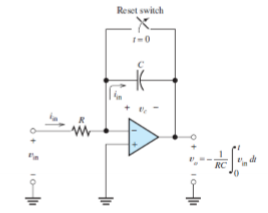
V at inverting op-amp input is 0 (summing point constraint); as current comes in, C charges; I through R and C is the same; Vo(t) = -1/RC |0 t (Vin(t)dt;

Op Amp - Low Pass

RC; integrator; gain will drop so that is why it is low pass

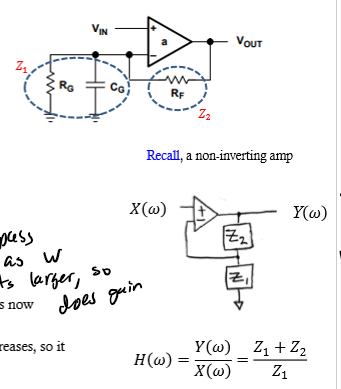
Op Amp - High Pass

as W gets larger, so does gain; gain = 1 + Z2/Z1 = 1 +((1 + jwCR)Rf)/Rg; differentiator

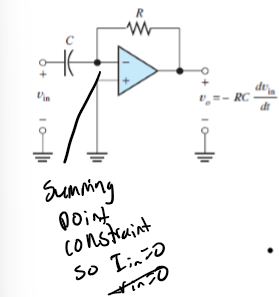
Differentiator

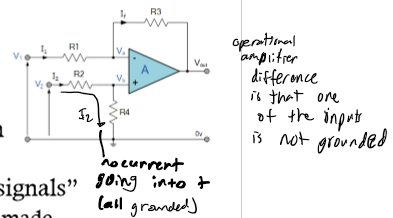
summing point constraint; CR; high pass; Gain = Vo/Vin = -Zr/Zc = -R / (1/jwc) = jwCR; have 2 input sources (used to measure difference between them); reject noise so gains are unequal (A1 does not equal A2) so Vout = A1Vin+ - A2Vin-; 0 output impedance and gain set by R3 and R1; input impedance at V2 is R2 + R4; voltage divider

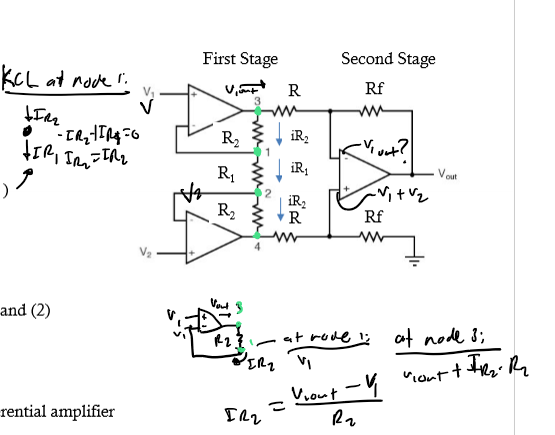
Instrumentation Amplifier

3 op amps but 2 stages; first stage = infinite input impedance and second stage is simply a unity gain (A = 1); use KCL

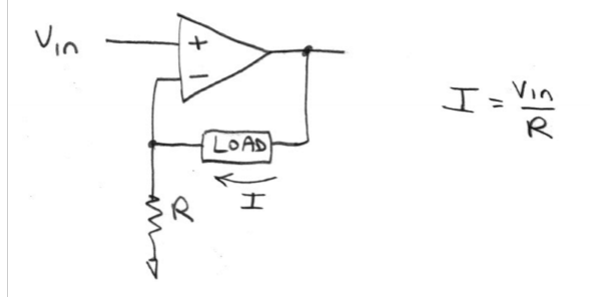
Current → Voltage Converter

Vout = -Is * Rf; used if measuring instrument is capable of only measuring V but you need to measure I; ex. photodiode sensor to measure light intensity

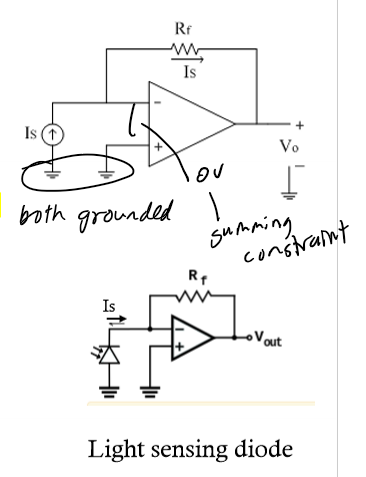
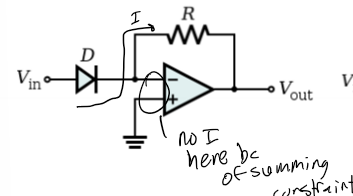
Exponential Amp

Vout = -e^(Vin); diode then R in an inverting op amp

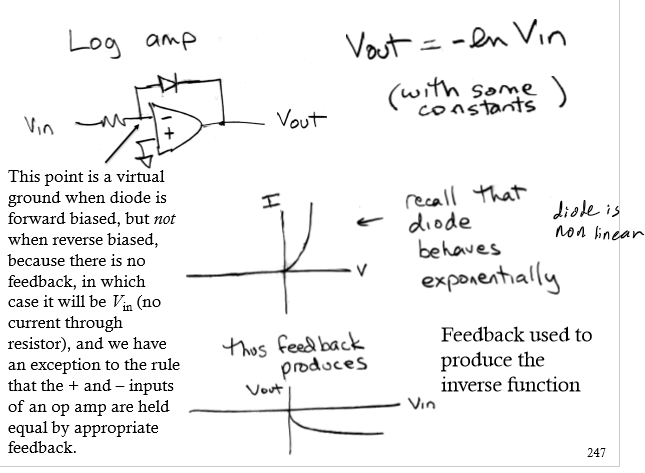
Log Amp

Vout = -ln (Vin); R then diode in an inverting op amp; virtual ground when diode is forward biased but not when reverse biased bc no feedback so Vin (no I through R) and exception to the rule that the + and - inputs of an op amp are held equal by appropriate feedback; feedback used to produce inverse function

Sinusoidal Oscillator

op amps model any linear differential eq.; all inverting amps w/ R and C