Self-Balancing Binary Trees

Searching Problem/Index System

• Set of entries: {𝑒1, … , 𝑒𝑛}

• Each entry 𝑒𝑖 is a pair (𝑘𝑖, 𝑣𝑖), where:

  •  𝑘𝑖 is a key value from some totally ordered domain, say integers or strings,

  • 𝑣𝑖 is an associated data value

• We assume keys are unique

• We do not use data values to solve the searching problem, but they will be important to the applications that use our data structure

Searching Problem

Given an arbitrary search key 𝑘, determine if there exists an entry matching this key value and if so, what the associated data value is

Dictionary (Map) ADT

• An ADT with operations insert, delete and find:

void insert(Key 𝒌, Value 𝒗): Stores an entry with the key-value pair (𝑘, 𝑣). (If 𝑘 is already present in the dictionary, error)

void delete(Key k): Deletes the entry associated with key 𝑘 from the dictionary. (If it does not exist, error)

Value find(Key k): Determine whether there is an entry in the dictionary associated with key 𝑘. If there is, return the associated value. Otherwise, return null reference

• You can also support iteration over the entries, range queries (enumerate or count all entries between some minimum and maximum value), returning 𝒊th smallest value as well as union and intersection

Sequential Allocation for Dictionary ADT

• Most naïve implementation: Store the entries in a linear array without sorting

  • To find key value, linear search -> 𝑂(𝑛) time

  • Insertion only takes 𝑂(1) time, if we still have enough space in the array. But checking for duplicates -> 𝑂(𝑛) time

• Otherwise, use a sorted (by key value) array

  • To find key value, binary search -> 𝑂(log 𝑛) time

    • For 𝑛 = 10^9 entries, log2 𝑛 ≤ 30

  • But updates (insertion and deletion) take 𝑶(𝒏) time as elements in array must be moved around to make space

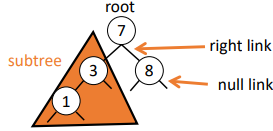
Binary Search Tree

at most two children per node - left child and right child

each node has a key-value pair, and are sorted by their keys

for each node its key is >= all keys in its left subtree, and < all keys in its right subtree

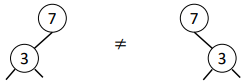
Are these Binary Trees Equal?

no

Setting Up Binary Search Tree ADT

public class BST<Key extends Comparable<Key>, Value> {
   private Node root;

   private class Node {
      private Key key;
      private Value value;
      private Node leftChild, rightChild;

      public Node(Key key, Value value) {
         this.key = key;
         this.value = value;
      }
   }
   ...
}

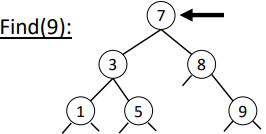
Implementing Find

Leverage the sortedness property:

1. If root has key, return root,

2. Else if key smaller, go left,

3. Else, go right

public Value find(Key key) {
   Node x = root;
   while (x != null) {
      int cmp = key.compareTO(x.key);
      if (cmp < 0) x = x.leftChild;
      //cmp < 0 == key < x.key
      else if (cmp > 0) x = x.rightChild;
      else return x.value; //cmp == 0
   }
   return null;
}

Time Complexity of Find

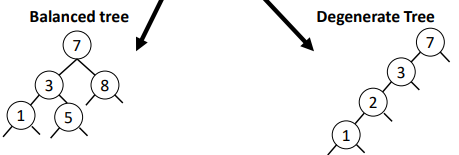
• For a BST of height ℎ, the worst-case complexity of find() is 𝑂(ℎ)

• Height of BST = Ω(log 𝑛) and 𝑂(𝑛)

• BST is very efficient on balanced trees, but inefficient on degenerate trees

Implementing Insertion

Need to maintain sortedness:

1. If x is null, insert new node

2. If x has key, give error,

3. Else if key < x’s key, recurse left

4. Else recurse right

public void insert(Key key, Value value) {
   root = inset(root, key, value);
}

private Node insert(Node x, Key key, Value value) {
   if (x == null) return new Node(key, value);
   int cmp = key.compareTo(x.key);
   if (cmp < 0) {
      x.leftChild = insert(x.leftChild, key, value);
   }
   else if (cmp > 0) {
      x.rightChild = insert(x.rightChild, key, value);
   }
   else System.out.println("Insert Exception");
      //x.value = value;
   return x;
}

Insertion Order Matters

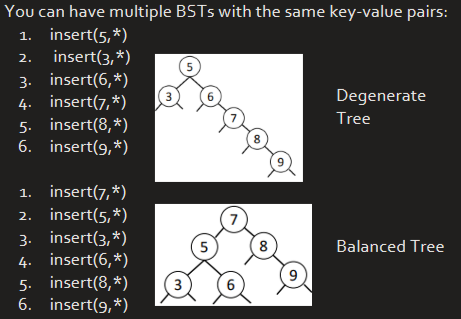
Time Complexity of Insertion

• For a BST of height ℎ, worst-case time complexity = 𝑂(ℎ)

• Depends on the insertion order

Implementing Deletion

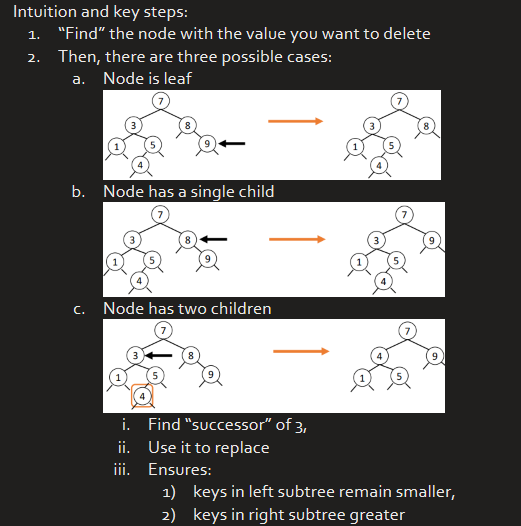
Code for delete()

successor of a node with value = node in tree with value just above that

private Node successor(Node x) {
   if (x == null || x.rightChild == null) return null;
   else {
      x = x.rightChild;
      while (x.leftChild != null) x = x.leftChild;
      return x;
   }
}

public void deleteMin() {
   root = deleteMin(root);
}

private Node deleteMin(Node x) {
   if (x.leftChild == null) return x.rightChild;
   else {
      x.leftChild = deleteMin(x.leftChild);
      return x;
   }
}

public void delete(Key key) {
   root = delete(root, key);
}

private Node delete(Node x, Key key) {
   if (x == null) return null;
   int cmp = key.compareTo(x.key);
   if (cmp < 0) x.leftChild = delete(X.leftChild, key);
   else if (cmp > 0) x.rightChild = delete(x.rightChild, key);
   else { //if we need to delete node x
      if (x.rightChild == null) return x.leftChild;
      else if (x.leftChild == null) return x.rightChild;
      else {
         Node t = x;
         x = successor(t);
         x.rightChild = deleteMin(t.rightChild);
         x. leftChild = t.leftChild;
      }
   }
   return x;
}

Self-Balancing Search Trees

There are many options, with diverse trade-offs

• 2-3 trees: tertiary self-balancing search trees

• AVL trees: self-balancing BST

• Red-black trees are a (BST) generalization of 2-3 trees

• B-trees: generalization of 2-3 trees to more keys per node

Some are not height-balanced:

• Splay Trees

• Treaps

For example, you may want your search tree to self-balance for common letter (key) patterns rather than for any letter (key) sequence

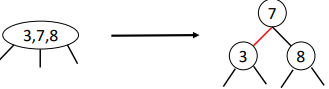
2-3 Trees

• 2-nodes: 1 key, 2 children

• 3-nodes: 2 keys, 3 children

• (Natural variant of) Inorder traversal gives keys in ascending order

• Perfectly balanced tree: Every path from the root to a leaf has the same length

• How do we maintain this property despite insertions and deletions?

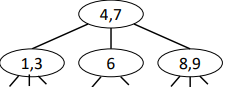
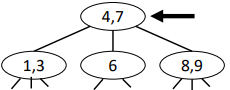
Find (2-3 Trees)

• Works (almost) just as in BSTs,

• Example: find(8)

Insertion (2-3 Trees)

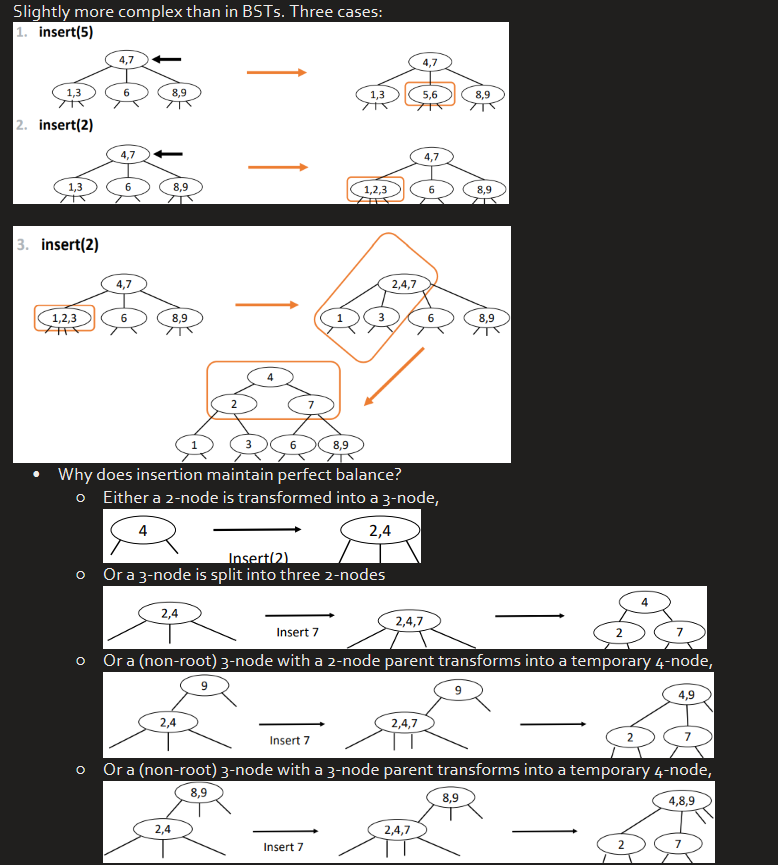
Cons of 2-3 Trees

• Quite inconvenient to implement

  • Different types of nodes (2-nodes and 3-nodes)

  • We need to do multiple compares at each node,

  • We need to move back up the tree to split 4-nodes 4. Large number of cases for that splitting

• Red-black trees are BSTs that build upon 2-3 trees, representing 3-node as a binary tree node with a red left link