CSCI 191T Part 2

Optimization

The selection of a best element (regarding some criterion) from some set of available alternatives
Problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of a function
Divided into two broad categories depending on whether the variables are continuous or discrete

Minimization

Given a function f: A → R from some set A to the real numbers:
Find element x_0 ∈ A such that f(x_0) ≤ f(x) for all x ∈ A
Typical to solve these since f(x_0) ≥ f(x) ⇔ -f(x_0) ≤ -f(x)

Maximization

Given a function f: A → R from some set A to the real numbers:
Find element x_0 ∈ A such that f(x_0) ≥ f(x) for all x ∈ A

Objective function

The function f
Defines how good a function is
Also known as loss function (minimization in ML), cost function (minimization in Economics), energy function (minimization in Physics), utility function (maximization in Multi-agent Systems), fitness function (maximization in EAs)

Trial and Error

Also known as brute force search, exhaustive search, generate and test
General problem solving technique and algorithmic paradigm that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's statement
Assumes 0 knowledge, but just needs to know rules
If we need only one solution then the search order followed can make a difference

Abstract brute force search algorithm

c

Brute Force attack

Consists of an attacker submitting many passwords or passphrase with the hope of eventually guessing correctly

Dictionary Attack

A type of brute force attack where an intruder attempts to crack a password protected security system with a dictionary list of common words and phrases used by businesses and individuals

Heuristic

A typically problem specific and empirical technique designed for speeding up searching techniques or to substitute them altogether
Introduce tradeoffs

Optimality

Heuristic tradeoff
Can the best solution be found?
May only find local optimum

Completeness

Heuristic tradeoff
Can all solutions be found?
May only find some

Accuracy and precision

Heuristic tradeoff
Are near-optimality guarantees provided? Are the solutions precise?

Execution time

Heuristic tradeoff
How fast are solutuon found?

Metaheuristic

Generally problem independent technique for searching that aims to avoid common tradeoff heuristic issues (usually by including stochasticity)
Guided search, as you search you accumulate knowledge and use the knowledge to guide the search
Search space of problem solutions

Hyperheuristic

A semi-mythical entity that seeks to automate, often by the incorporation of machine learning techniques, the process of selecting, combining, generation or adaption several simple heuristics (or components of such heuristics) to efficiently solve computational search problems
Always search within a search space of heuristics

Continuous Optimization

Find the min/max of a continuous function
Select from Real Numbers and find the best
Allows for the use of calculus techniques in a straightforward manner

Discrete Optimization

Also known as combinatorial
Find the min/max from the set of countable numbers
Ex: TSP and N-Queens

Random Search Algorithm

Initialize x // x is candidate solution and is initialized randomly
Until terminal condition is met: // Terminal condition can involve the number of iterations or adequate fitness reached
new position x' // new position from hypersphere of a given radius surrounding the current position x
if f(x') < f(x): // f:R^n -\> R is the fitness or cost function that must be minimized
x \= x' // Move to a new position

Gradient Descent or Ascent

A first order iterative optimization algorithm for finding the minimum or maximum of a function
First derivative of the objective function is used
Iteratively mode in the opposite direction of the gradient for descent while for ascent we move along the gradient

Gravity

Described as a natural phenomenon by which all things with mass or energy are brought toward (or gravitate toward) one another
The physical connection between spacetime and matters that causes a curvature of spacetime
Perfect in discovering minima

Loss Function

Gravity Analogy: Potential Energy
Gradient Descent:

Minimize Loss Function

Gravity Analogy: Minimize Potential Energy
Gradient Descent:

Differential calculus

A function f(x) is called differentiable at x \= a if f'(a) exists
If f(x) is differentiable at x \= a then f(x) is continuous at x \= a

Derivatives

The number of f'(c) represents the slope of the graph y \= f(x) at the point (c, f(c))
Represents the rate of change of y with respect to x when x is near c

Partial derivative

Used when we need one derivative per dimension
This of a function of several variables is its derivative with respect to one of those variables, with the others held constant

Gradient vector

Also known as Nabla
The vector that its coordinates are the partial derivatives of the function
Points in the direction of the greatest increase of the function

Find optimum of a function

Given its derivatives, we need to
- Find all stationary points (where the derivative, or all partial derivatives, become 0). These points will either be a minima, maximum, or saddle points
- Further, examine these points using higher order derivatives or simple evaluation to identify a minimum (Make the search space smaller)

Position in Gradient Descent

Abstract Gradient Descent Algorithm
A particular point from the domain of the function we seek to minimize/optimize

Gradient in Gradient Descent

Abstract Gradient Descent Algorithm
Gradient descent requires the derivative of the function at each point traverses

Learning rate in Gradient Descent

Abstract Gradient Descent Algorithm
Gradient descent works by following a step proportional to the gradient
Indicates the proportionality (how big or small)
Typically less than 0.1
If too small -\> convergence
If too big -\> might jump over minimum

Initialization in Gradient Descent

1st step of Abstract Gradient Descent Algorithm
We start randomly at a particular point
Ex: x_0 \= 4, f(x_0 \= 4) \= 66

Calculate gradient

2nd step of the Abstract Gradient Descent Algorithm
x_t+1 \= x_t + 𝚫x

Formula for Gradient Descent

x = -𝛼∇f(x_t) + (step)

Formula for Gradient Ascent

x = +𝛼∇f(x_t) + (step)

Execute step for Gradient Descent

3rd step of Abstract Gradient Descent Algorithm
Update
temp0 \= x_0 - 𝛼d/dx_0 J(x_0, x_1)
temp1 \= x_1 - 𝛼d/dx_1 J(x_0, x_1)
x_0 \= temp0
x_1 \= temp1

Termination for Gradient Descent

4th step of Abstract Gradient Descent Algorithm
Many criteria exist
- When number of iteration exceeds a pre-specified number
- The step becomes smaller than 𝜀

Abstract Gradient Descent Algorithm

Start from a random point
Until terminal condition is met:
Move according to the gradient vector of the current position

Problems of Gradient Descent

Choosing a learning rate
Falling into a local minimum

Learning Rate Schedule

Decaying learning rates can speed up learning at the beginning and slow down towards the end
Varying learning rate can also avoid local minima
Different types of these have different properties
In multivariate objective functions we have have different these for each dimension
Adjusting can be highly beneficial

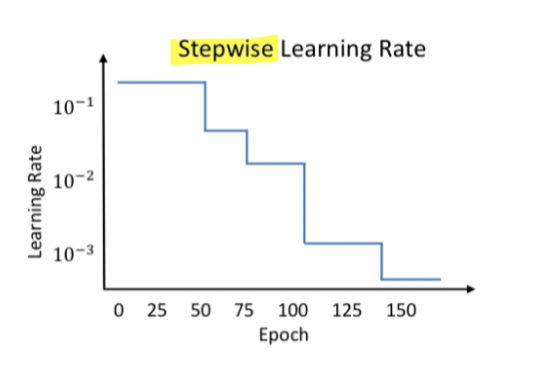
Stepwise Learning Rate

Learning rate schedule - Decay
Quite popular
The learning rate is reduced by some percentage after a set of training epochs

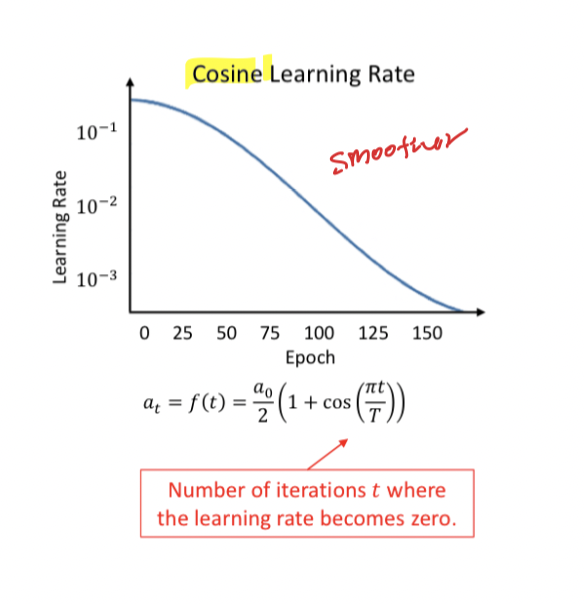
Cosine Learning Rate

Learning rate schedule - Decay
Popular
Begin with the full learning rate, then use the cosine decay to converge to a minimum

Periodicity Learning Rate Schedule

Learning rates with random restarts can help avoid local minima
- Trying different starting points
- Spending CPU time to explore the space is much better than spending it to do sophisticated optimizations in many cases

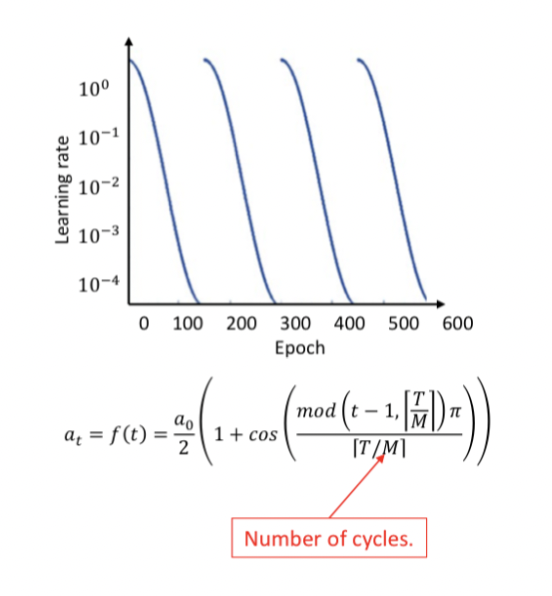
Cyclic cosine decay

Learning rate schedule - periodicity
Lower the learning rate at a fast pace, this encourages convergence to a local minimum
Increase the learning rate, this pushes out of a local minimum

Adaptive Learning Rate

Learning rate can be adapted according to the gradient so that is decreases with convergence in a principles manner and for each dimension
learning rate can adapt to the general "curvature of flatness" of each dimension

Adagrad

Also known as adaptive gradient
A modified gradient descent algorithm which keeps track of the squared gradient and uses them to adapt the gradient in different directions
Informally, this increases the learning rate for sparser parameters (Flat) and decreases it for the less sparse ones (non flat)
Focuses on updating features that haven't been updated enough yet

Adagrad formula

For all dimensions i:
x_t+1,i \= x_t,i - a_i/(e + sqrt(V_t+1,i)) * d/dx_t,i f(x_t)
V_t+1,i \= V_t,i + (d/dx_t,i f(x_t))^2
- a_i is the base learning rate for each dimension (typically 0.001)
- e is a small scalar (e.g. 10^-8) used to prevent division by 0
- V_t+1 is the summation of all gradients squared from the beginning to timestep t + 1

RMSProp

Well known yet unpublished algorithm
Similar to Adagrad
Motivation was to find an algorithm that effectively deals with the diminishing learning rates of Adagrad, while still having a relatively fast convergence
Way to speed up learning by penalizing the update of those parameters that lead to unnecessarily high oscillation of the objective function
Decay rate allows it to keep the square under a manageable size the whole time

Problem with Adagrad

Use the square since it's differentiable and penalizes outliers
If the space is curvy all over then it will have a slower convergence with time since you keep adding squares

RMSProp formula

For all dimensions i:
x_t+1,i \= x_t,i - a_i/(e + sqrt(V_t+1,i)) * d/dx_t,i f(x_t)
V_t+1,i \= 𝛾V_t,i + (1-𝛾)(d/dx_t,i f(x_t))^2
- a_i is the base learning rate for each dimension (typically 0.001)
- e is a small scalar (e.g. 10^-8) used to prevent division by 0
- V_t+1 is the summation of all gradients squared from the beginning to timestep t + 1
- 𝛾 is the forgetting factor, how much we care about the past

Momentum

In Newtonian mechanics, it is the product of mass and velocity of an object. It is a vector quantity possessing a magnitude and direction
p \= mv where m is the mass and v is the velocity

Gradient Descent with momentum

Determines the next update as a linear combination of the current gradient and the past step
Moves faster because the momentum it can propel itself out of local minima
Adding randomness in the step direction can further enhance the exploration aspects of the algorithm

Gradient Descent with momentum formula

For all dimensions i
x_t+1,i \= x_t,i - 𝛼_i M_t+1, i
M_t+1,i \= d/dx_t,i f(x_t) + 𝛾M_t,i
𝛼 is the step size with 𝛼 ≠ 0 (typically 0.001)
𝛾 is an exponential decay factor with 𝛾 ∈ (0, 1) typically 0.9
M_t+1,i is the momentum adjusted gradient

Adaptive Moment Estimation (Adam)

Combines the Momentum and RMSProp best features
Arguably an improvement over the previous algorithms
Combines the speed and "pushing" properties from momentum and the ability to adapt gradients per dimension while keeping them bounded from RMSProp
Works well in practice and is typically among the first choices in optimization problems

Adaptive Moment Estimation Formula

For all dimensions i:
- M_t,i \= 𝛾_1 M_t-1,i + (1-𝛾_1) d/dx_t,i f(x_t)
- V_t,i \= 𝛾_2 V_t-1,)i + (1-𝛾_2)(d/dx_t,i f(x_t))^2
- M_t,i \= M_t+1,i / (1-𝛾_1^t), V_t,i \= V_t+1,i / (1-𝛾_2^t)
x_t+1,i \= x_t,i - a_i(M_t,i / 𝜀+sqrt(V_t,i))
Where 𝛾_1 and 𝛾_2 are the forgetting factors of gradients and second moments of gradients respectively (typically 𝛾_1 \= 0.9 and 𝛾_2 \= 0.999)
𝜀 is a small scalar (e.g. 10^-8) used to prevent division by 0
M_t,i is the running average of the gradients
V_t,i is the running average of the second moments of gradients

Exploitation in Gradient Descent

Moving along the gradient pushes towards quality
Tricks:
- Big learning rate moves fast but can oscillate over the optimal
- Small learning rate increases precision

Exploration in Gradient Descent

Moving in a stochastic manner pushes towards novelty
Tricks
- Decay learning rate restarts can lead to better exploration
- Restarts can help evenly explore the space

Rastrigin Function

A non-convex function typically used as a performance test problem
Has a global minimum at x \= 0 where f(x) \= 0

Multiobjective Optimization

Concerned with optimization problems involving more than one objective function to be optimized simultaneously
Ex:
- Minimizing cost while maximizing comfort while buying a car
- Maximizing performance whilst minimizing fuel consumption
Solving this type of problem does not have the same straightforward meaning as for a single optimization problem

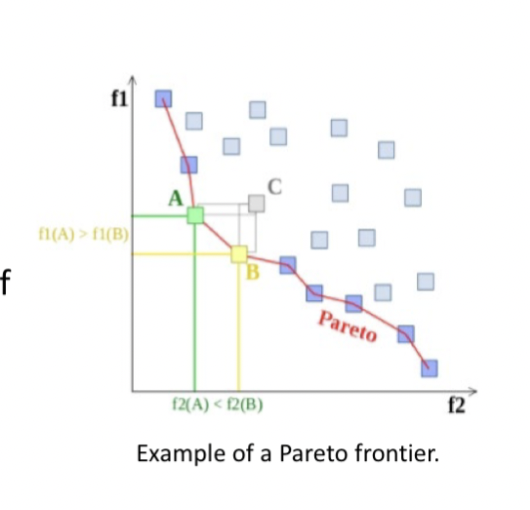
Pareto Optimality

In nontrivial multi-objective optimization:
- No single solution exists that simultaneously optimizes each objective
- The objective functions are conflicting
- There exists a (possibly infinite) number of Pareto optimal solutions

Pareto optimal solutions

Solutions that cannot be improved in any of the objectives without degrading at least one of the other objectives

No preference methods

One of the ways to solve a multi-objective optimization problem
No decision maker is assumed, and a compromise solution is identified without any preference informations

A priori methods

One of the ways to solve a multi-objective optimization problem
Preference information is first provided by the decision maker and then a solution best satisfying these preferences is identified

A posteriori Methods

One of the ways to solve a multi-objective optimization problem
A set of Pareto optimal solutions is first found and then the decision maker chooses one of them

Interactive methods

One of the ways to solve a multi-objective optimization problem
The decision maker iteratively searches the space of Pareto optimal solutions

Scalarization

For a multi-objective means formulating a single-objective optimization problem such that the optimal solutions to the single objective problem are Pareto optimal solutions to the multi-objective optimization problem
Often requires that every Pareto optimal solution can be reached with some parameters of the scalarization

Weighted Sum Method

Scalarize a set of objectives into a single objective by adding each objective pre-multiplied by a user-supplied weight
Minimize F(x) \= ∑M, m\=1 w_m F_m(x)
Subject to g_i (x) \>\= 0, h_k (x) \= 0, x_i ^L

epsilon contraint method

A very well known scalarization method
min f(x), f_j (x), s.t. x∈X
f_i (x)

Consciousness

The awareness of internal or external stimuli
Product of the maturity of intelligence

Tropism

Indicates the growth or turning movement of a biological organism, usually a plant, in response to an environmental stimulus (typically plants or sessile animals)

Reflex

An involuntary and nearly instantaneous movement in response to a stimulus (typically for animals)

Instinct

The inherent inclination of a living organism towards a particular complex behavior (typically for animals)

Non-associative learning

Also known as Simple Learning
Refers to "a relatively permanent change in the strength of response to a single stimulus due to repeated exposure to that stimulus", with the exemption of changes caused by sensory adaptation, fatigue, or injury
No association between stimulus and response

Habituation

Type of non-associative learning
One or more components of an innate response (e.g. response probability, response duration) to a stimulus diminishes when the stimulus is repeated
Intensity of the response becomes less and less (getting used to it)
Ex: Crows present in field, scared away when scarecrow is introduced, prolonged exposure to scarecrow means they come back

Sensitization

Type of non-associative learning
The progressive application of a response that follows repeated administrations of a stimulus
Ex: At first when a neighbor is loud it does not bother you but as it keeps happening it bothers you

Associative Learning

Also known as complex learning
A great adaptation mechanism but very restrictive as it can not leads to new associations between stimuli and responses
The process by which a person or animal learns an association between two stimuli or events

Imprinting

Type of associative learning
A phase-sensitive learning (occurring at a particular age or a particular life stage) that is rapid and apparently independent of the consequences of behavior (it just happens at a specific time)
Ex: baby duck will learn to follow the first organism they see

Classical Conditioning

Type of Associative learning
Refers to a learning procedure in which a biologically potent stimulus (e.g. food) is paired with a previously neutral stimulus (e.g. a bell)
Not teaching new behaviors just linking pre-existing behaviors to stimuli (focuses on elicited behaviors)
Response is a reflex and involuntary

Neutral Stimulus (NS)

1st component of classical conditioning
A stimulus that provokes no reflexive response
Ex: In Pavlov's dog, the bell at the beginning

Unconditioned Stimulus (UCS)

2nd component of Classical Conditioning
A stimulus that provokes a reflexive response
Ex: In Pavlov's dog, the food at the beginning

Unconditioned Response (UCR)

3rd component of Classical Conditioning
The reflexive response
Ex: In Pavlov's dog, the dog drooling

Conditioned Stimulus (CS)

4th component of classical conditioning
The originally neutral stimulus that gains the power to cause the response
Ex: in Pavlov's dog, the bell being rung causing the dog to drool

Conditioned Response (CR)

5th component of Classical Conditioning
The unconditioned response that is now associated with the unconditioned stimulus
Ex: In Pavlov's dog, the dog drooling because of the bell

Acquisition

The learning phase during which a UCR transforms itself into a CR and comes to be elicited by the CS
A NS is paired with the UCS

Learning trial

In classical conditioning it is each pairing made during acquisition
Typically many are needed

Forward pairing

Basic pairing type in classical conditioning
The onset of the CS precedes the one of the US in order to signal that the US will follow
Ex: The bell is rung then the food is given

Simultaneous Conditioning

Basic pairing type of classical conditioning
The CS and US are presented and terminated at the same time
Ex: The bell is rung and food is given at the same time

Backward conditioning

Basic pairing type of classical conditioning
Occurs when a CS immediately follows a US
Ex: Food is given then bell is rung

How to learn fast

Repeated CS-UCS pairing
UCS is intense (larger amount of food, traumatic event)
- One trial learning is possible is such case
Forwards pairing where the time interval between the CS and UCS is short
Consistency is important
- If the CS is paired with the US, but the US also occurs at other times then conditioning fails

Stimulus Discrimination

Classical Conditioning
A CR occurs in the presence of one stimulus but not others
Ex: Drooling may not be elicited by a piano key

Stimulus Generalization

Classical Conditioning
Stimuli like the initial CS elicit a CR
Ex: Drooling be may elicited by a whistle or doorbell
Trauma
- Intense UCS and stimulus generalization

Higher-order conditioning

Classical conditioning
Occurs when a neutral stimulus becomes a CS after being paired with an already established CS
Ex: Can opener + food \= drooling, squeaky cabinet door + can opener \= drooling, squeaky cabinet door \= drooling

Temporal Conditioning

Classical Conditioning
A US is presented at regular intervals, for instance very 10 minutes. Conditioning is said to have occurred when the CR tends to occur shortly before each US
Suggests that animals have a biological clock that can serve as a a CS
Ex: After time period present food continuously, then after time period dog will drool

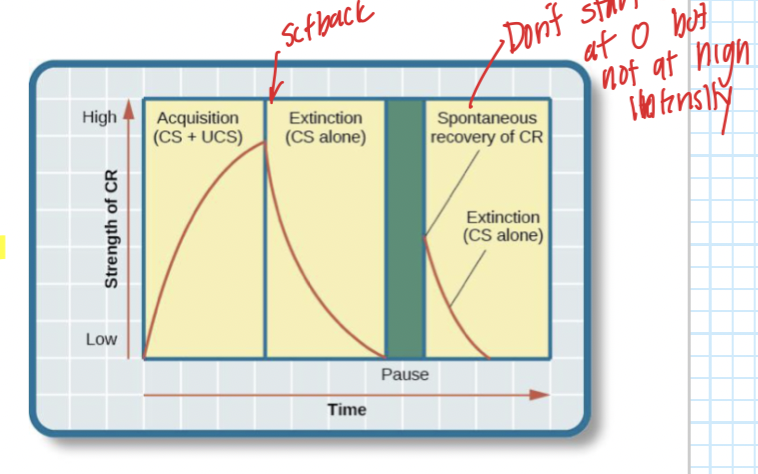
Extinction

The diminishing (or lessening) of a learned response, when an unconditioned stimulus does not follow a conditioned stimulus
CS is presented repeatedly in the absence of the UCS, causing the CR to weaken and eventually disappear

Extinction trial

Classical conditioning
Each time the CS occurs without the UCS

Spontaneous Recovery

Reappearance of a previously extinguished CR after a rest period and without new learning trials
This is usually weaker than the initial CR and extinguishes more rapidly

Preparedness

Animals are biologically predisposed to learn some associations more easily than others
Association related to a species' survival are learned more easily
Ex: Conditioned taste aversions are conditioned fear response are both influence by this

Applications of Classical Conditioning

Behavior therapies based on classical conditioning
Classically conditioned behaviors can also affect our health

Operant Conditioning

Type of Associative learning
A behavior that is reinforced or punished in the presence of a stimulus becomes more or less likely to occur in the presence of that stimulus
Behavior changes as a result of the consequences that follow it
Focuses of emitted behaviors (learn new behaviors)
Emotions are essential
Response is voluntary behavior

Thorndike's Law of Effect

Responses that produce a satisfying effect in a particular situation become more likely to occur again in that situation, and responses that produce a discomforting effect become less likely to occur again in that situation

Discriminative Stimulus

Operant Conditioning
Identify WHEN to respond
Signal that a particular response will now produce certain consequences
Sets the occasion for a response to be reinforced
Ex: A light in the Skinner box may indicate whether food will be dispense when the lever is pressed and might induce a certain behavior