PNB 3XE3 Midterm 2

Family-wise error rate (FWER)

• The probability of making at least one Type I error (false positive) across a family of related statistical tests

  • When alpha = .05, each test has a 5% chance of being wrong

  • If we run several tests, the chance of error accumulates

ANOVA

• Analysis of variance

• We use it when there are more than two levels

What types of variance does an ANOVA consider?

• Total variability between individuals

• Variability between groups

• Variability within groups

Total variability between individuals

Regardless of group membership, each data point is measured relative to the grand mean

Between groups variance

• How similar is each group mean to the grand mean?

• If all the groups came from the same population then they should all have similar group means

• Variation due to the independent variable

Within group variance

• How similar/messy are the scores within each group?

• This is the random variability we cannot account for (“residual variance”, “error variance”, “random error”)

What does an ANOVA do?

An ANOVA compares the BETWEEN group variability to the WITHIN group variability

How is an ANOVA similar to a t-test? How is an ANOVA different from a t-test?

• Both tests measure a ratio of the difference between means (variability between groups) over the amount of variability within each group

• A t-test compares the means of two groups, whereas an ANOVA compares the means of three or more groups (or conditions)

One-way ANOVA

Determines whether there are significant differences among the means of three or more independent groups that differ along one factor (IV)

One-way ANOVA hypotheses

Null hypothesis: all group means are equal

Alternative hypothesis: at least one group differs from the others

What does it mean that ANOVA is an omnibus test?

It doesn’t test specific pairwise differences

F-statistic

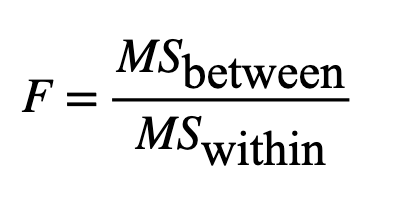
F-test steps

• Compute the F-statistic

• Determine the F critical value Fα, _{(dfbetween, dfwithin)}

  • Based on the chosen significance level (α) and TWO degrees of freedom (df_between and df_within)

• Compare

  • If F_obs > Fα, _{(dfbetween, dfwithin)}, reject H₀

F distribution

A probability distribution of a ratio of two variances, each scaled by their own degrees of freedom

Partition of variance

ANOVA partitions (splits) the total variability in the data into different sources, explaining where the variation comes from

Eta squared (η²)

• Effect size in ANOVA

• The proportion of total variance explained by the factor/group

• Ranges from 0 to 1

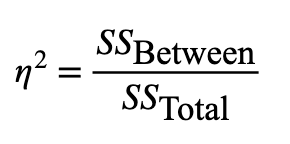
Why don’t we run pairwise t-tests between all group means when there are more than 2 groups?

• Each t-test has its own chance (e.g. 5%) of a Type I error (false positive)

• If we run many t-tests, these error accumulate, leading to the overall (family-wise) error rate much higher than (5%)

Post-hoc (after the fact) corrections

Any statistical adjustment made after running multiple tests to control the overall chance of false positives (e.g. family-wise error rate)

Bonferroni correction

Divides α by the number of tests (α/m)

Holm correction (sequential Bonferonni)

Sequentially adjusts p-values (step-down)

Tukey HSD (Honest Significant Difference)

Adjusts CIs/p-values for all pairwise mean comparisons in ANOVA

Benjamin-Hochberg (FDR)

Controls expected proportion of false discoveries

What are the three assumptions of ANOVA?

• Independence of observations

• Normality

• Homogeneity of variances, tested with Levene’s test

T-test

Determines whether there is a difference between the means of two groups or between a group mean and a theoretical value

Factorial (or ‘two-way’) ANOVA

A statistical model that examines how two or more independent variables (factors) jointly influence a dependent variable

Factorial ANOVA pros

• Tests multiple factors together

• Controls Type I error across multiple factors

• Can reduce residual variance

• Detects interactions: richer theoretical insight

Factorial ANOVA cons

• More complex interpretation, especially with interactions

• Requires balanced or larger samples for stable estimates

• Higher risk of violations of orthogonality or unequal n complicate results

• Added complexity may be unnecessary when only one factor is theoretically relevant

Factor

An independent variable that is manipulated or observed to examine its effect on the dependent variable (e.g. Face Ethnicity, Speech Type)

Level

A specific category or value within a factor (e.g. Asian, Caucasian, African)

Cell (or condition)

A unique combination of levels across all factors - each represent one experimental condition (e.g. Asian & Native)

Main effect

The overall effect of one factor on the dependent variable, averaging across all levels of the other factor(s)

Simple effect

The effect of one factor at a specific level of another factor (e.g. difference among ethnicities when speech is native)

Interaction effect

When the effect of one factor depends on the level of another factor (e.g. the ethnicity effect changes depending on whether speech is native or non-native)

What are the two features of a factor (IV)

• Categorical - each factor consists of discrete levels (e.g. male vs. female)

• Orthogonal (ideally) - factors are designed to be independent

What are the features of a dependent variable?

• Continuous - must be quantitative, allowing computation of means and variances (e.g. reaction time)

• Normally distributed within groups - scores within each cell should roughly follow a normal distribution

Margin means

The means for one factor averaging over (collapsing across) the levels of other factors

Expected cell mean

The model’s expected cell outcome for a group (assumes there are no interactions)

Partial eta squared η_p²

• Effect size in factorial ANOVA

• The proportion of variance explained by a given effect relative only to the variance it competes with (i.e. that effect + its residual error)

• Ranges from 0 to 1

Repeated measures (rm) ANOVA

• Extension of the paired-sample t-test

• A statistical model used to test whether mean differences exist across multiple measurements taken from the same participants (or experimental units) under different conditions or at different times

• Removes stable individual differences from the error term, improving sensitivity to detect within-subject effects

One-way ANOVA model

SS_total = SS_between + SS_{within(error)}

Factorial ANOVA model

SS_error = SS_A + SS_B + SS_AxB + SS_{within(error)}

Repeated measures ANOVA model

SS_total = SS_between + SS_participants + SS_{error(within)}

sphericity assumption

• In rmANOVA, the variances of the differences between all pairs of within-subject conditions are equal

• Var(A - B) = Var(A - C) = Var(B - C)

• We can test this using Mauchly’s test for sphericity

What happens if sphericity is violated?

• The F-statistic will be too liberal, thus the Type I error rate increases

• To fix this, a correction to the degrees of freedom (e.g. Greenhouse-Geisser or Huyn-Feldt) can be applied

simple effect analysis

• We use it after finding a significant interaction in a factorial ANOVA to identify where the interaction lies

deviation from the expected cell mean

• Tells us how much the observed score differs from what we would expect if there were no effects (main effects or interactions)

• How surprising/unexplained the score is

residual

• The difference between an observed value and the value predicted by your model

• Tells you how far off your model’s prediction was for a given value