Work and Energy

Energy

• Property of a system that allows it to do work or cause change.

• All forms of energy (kinetic, potential, thermal, etc.) are measured in joules (J) in the SI system.

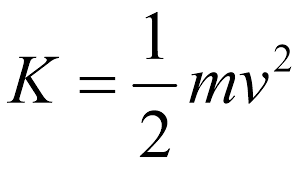
Kinetic Energy

• Energy associated with the motion of an object.

• Depends on mass and speed squared (scalar quantity; does not depend on direction).

• Formula:

KE = 1/2mv²

Potential Energy

• Energy stored in a system that can be converted into work or motion.

• Types include:

  • Gravitational: U = mgh

  • Elastic: U = ½ kx²

  • Electrical

  • Chemical

Gravitational Potential Energy (GPE)

• Energy an object has due to its position in a gravitational field.

• Depends on:

  • Mass (m)

  • Height (h) above a reference point (datum)

  • Gravity (g)

• Formula: U = mgh

Elastic Potential Energy

• Energy stored in a stretched or compressed spring (or elastic object).

• Depends on:

  • Spring constant (k) — stiffness of the spring

  • Displacement (x) — how much the spring is stretched or compressed

• Formula: U = ½ kx²

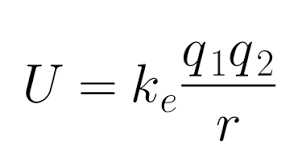
Electrical Potential Energy

• Energy stored due to the position of charged particles relative to each other.

• Depends on:

  • Magnitude of charges (q₁,q₂)

  • Distance between them (r)

• Formula (Coulomb’s law form):

U = (k_e) (q₁q₂/r)

Chemical Potential Energy

• Energy stored in the chemical bonds of molecules or compounds.

• Released or absorbed during chemical reactions.

Mechanical Energy:

• Total energy of a system due to motion and position.

• Formula:

E_mechanical = KE + PE

• KE = kinetic energy

• PE = potential energy (gravitational, elastic, etc.)

Conservative Forces

• Path independent: Work done depends only on initial and final positions, not the path taken.

• Do not dissipate mechanical energy — total mechanical energy is conserved.

Conservation of Mechanical Energy

• If only conservative forces act, the total mechanical energy (KE + PE) is constant.

• Examples of conservative forces:

  • Gravity

  • Electrostatic forces

  • Elastic (spring) forces — nearly conservative in real situations.

Nonconservative Forces

• Path dependent: Work done depends on the path taken.

• Dissipate mechanical energy — convert it into other forms (e.g., heat, sound).

Effects of Nonconservative Forces

• Total energy is still conserved, but some mechanical energy is transformed into thermal, chemical, or other forms.

• Examples of nonconservative forces:

  • Friction

  • Air resistance

  • Viscous drag

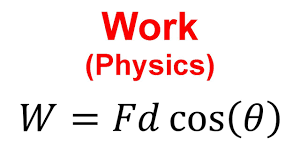
Work

• Definition: A process by which energy is transferred from one system to another.

• Work involves a force applied over a distance in the direction of the force.

• Formula:

W = F⃗⋅d⃗ = Fd cos⁡θ

Work in Thermodynamics

• Definition: Energy transferred when a system expands or compresses against external pressure.

• Formula:

W = Area under a Pressure–Volume (P–V) curve

• Sign convention:

  • W>0 → work done by the system

  • W<0 → work done on the system

Power

• Definition: The rate at which work is done or energy is transferred.

• Formula:

P = W/t

• W = work

• t = time

• SI unit: watt (W), where 1 W = 1 J/s

Work–Energy Theorem

• Definition: When net work is done on or by a system, the system’s kinetic energy changes by the same amount:

W_net = ΔKE

• More generally, work can also be transferred into other forms of energy (potential, thermal, etc.).

Mechanical Advantage

• Factor by which a simple machine multiplies the input force.

• Formula:

Mechanical Advantage = F_out/F_in

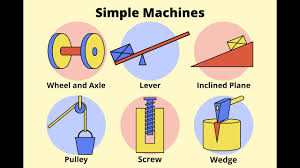
Six Simple Machines

• Types:

  1. Inclined plane

  2. Wedge

  3. Wheel and axle

  4. Lever

  5. Pulley

  6. Screw

• Purpose: Provide mechanical advantage, making work easier by multiplying force or changing its direction.

Mechanical Advantage and Work

• Effect: Makes it easier to accomplish work by reducing the input force.

• Trade-off: The distance over which the input force is applied increases by the same factor.

• Assumption: 100% efficiency (no energy lost).

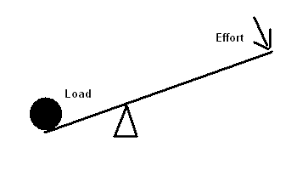
Load vs Effort in Simple Machines

• Load: The output force of a machine. Acts over load distance → determines work output.

• Effort: The input force applied to the machine. Acts over effort distance → determines work input.

Efficiency of a Machine

• Definition: Ratio of work output to work input, accounting for nonconservative forces (like friction).

• Formula:

Efficiency = W_out/W_in ×100

Zeroth Law of Thermodynamics:

• If two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.

• If system A is in thermal equilibrium with system B, and system B is in thermal equilibrium with system C, then A and C are in equilibrium.

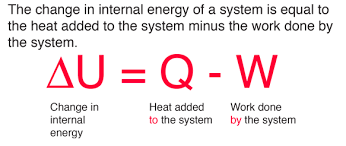
First Law of Thermodynamics:

• Energy cannot be created or destroyed, only transformed.

• ΔU = Q-W

• ΔU: change in internal energy

• Q: heat added to the system

• W: work done by the system

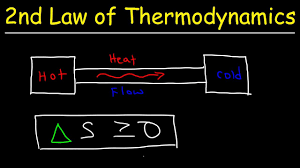
Second Law of Thermodynamics:

• In any real (irreversible) process, the entropy of the universe increases.

ΔS universe ≥ 0

• Heat flows spontaneously from hot to cold, not the other way around.

Third Law of Thermodynamics:

• The entropy of a perfectly ordered crystalline substance approaches zero as temperature approaches absolute zero.

S→0 as T→0K

What is the condition for isothermal expansion of an ideal gas?

Temperature stays constant

(ΔT=0 ⇒ ΔU=0)

What is the condition for adiabatic expansion?

No heat exchange (Q=0).

What is the condition for an isobaric process?

Pressure is constant (P = constant).

What is the condition for an isochoric process?

Volume is constant (ΔV=0).