Ch. 10 Sequences and Series - Precalculus
5.0(3)
5.0(3)
Card Sorting
1/22
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
23 Terms
1
New cards
Convergent sequence
Has a limit such that the terms approach a unique number
2
New cards
Divergent sequence
The terms don’t approach a finite number
3
New cards
Series
* Indicated sum of all the terms of a sequence
* Finite & infinite
* Finite & infinite
4
New cards
nth Partial Sum (Sₙ)
The sum of the first n terms of a series
5
New cards
Recursive formula for arithmetic sequence
aₙ = aₙ₋₁ + d
6
New cards
Explicit formula for arithmetic sequence
aₙ = a₁ + (n-1)d
7
New cards
Arithmetic sequence with 2nd differences
* Quadratic
* aₙ = an² + bn + c
* aₙ = an² + bn + c
8
New cards
nth Partial Sum of an Arithmetic Series
* Sₙ = (ⁿ/₂)(a₁ + aₙ)
* Sₙ = (ⁿ/₂)\[2a₁ + (n-1)d\]
* Sₙ = (ⁿ/₂)\[2a₁ + (n-1)d\]
![* Sₙ = (ⁿ/₂)(a₁ + aₙ)
* Sₙ = (ⁿ/₂)\[2a₁ + (n-1)d\]](https://knowt-user-attachments.s3.amazonaws.com/bd633138ebb2499ab9937a5bceb95eb2.jpeg)
9
New cards
Recursive formula for geometric sequence
aₙ = aₙ₋₁・r
10
New cards
Explicit formula for geometric sequence
aₙ = a₁・rⁿ⁻¹
11
New cards
nth Partial Sum of a Geometric Series
* Sₙ = a₁\[(1-rⁿ)/(1-r)\]
* Sₙ = (a₁-aₙr)/(1-r)
* Sₙ = (a₁-aₙr)/(1-r)
![* Sₙ = a₁\[(1-rⁿ)/(1-r)\]
* Sₙ = (a₁-aₙr)/(1-r)](https://knowt-user-attachments.s3.amazonaws.com/7505246f9a3a4af187cb0a31b5f3be7c.jpeg)
12
New cards
Sum of an Infinite Geometric Series
S = a₁/(1-r)
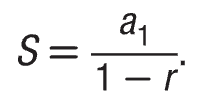
13
New cards
Pascal’s Triangle
A triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression, such as (x + y)ⁿ
* Recursive: coefficients in the (n-1)th row can be added together to find coefficients in the nth row
* Recursive: coefficients in the (n-1)th row can be added together to find coefficients in the nth row
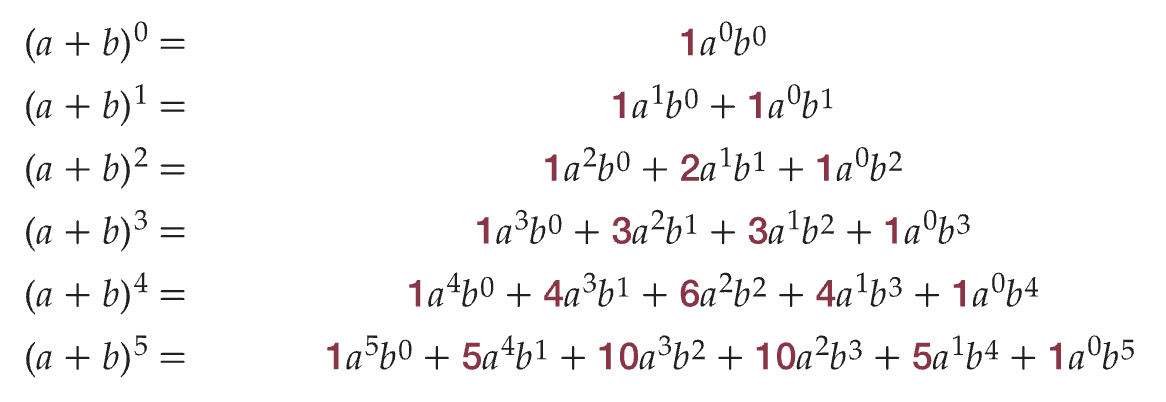
14
New cards
Formula for Binomial Coefficients of (a + b)ⁿ
ₙCᵣ = n!/\[(n-r)!r!\]
* For the aⁿ⁻ᣴbᣴ term
* For the aⁿ⁻ᣴbᣴ term
![ₙCᵣ = n!/\[(n-r)!r!\]
* For the aⁿ⁻ᣴbᣴ term](https://knowt-user-attachments.s3.amazonaws.com/9afde3a9c3e2415193424ebcb75b7726.jpeg)
15
New cards
Formula for Binomial Experiments of (p + q)ⁿ
ₙCₓ・pˣ qⁿ⁻ˣ
* x = successes
* n = # of trials
* x = successes
* n = # of trials
16
New cards
Binomial Theorem
(a + b)ⁿ = ₙC₀ aⁿb⁰ + ₙC₁ aⁿ⁻¹b¹ + ₙC₂ aⁿ⁻²b² + … + ₙCᵣaⁿ⁻ᣴbᣴ + ₙCₙ a⁰bⁿ
* r = 0, 1, 2, … , n
* r = 0, 1, 2, … , n
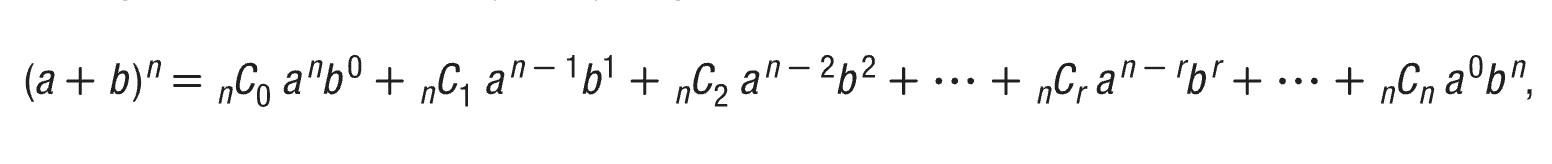
17
New cards
Power Series
* Infinite
* x & aₙ take on any values for n = 0, 1, 2, …
* x & aₙ take on any values for n = 0, 1, 2, …
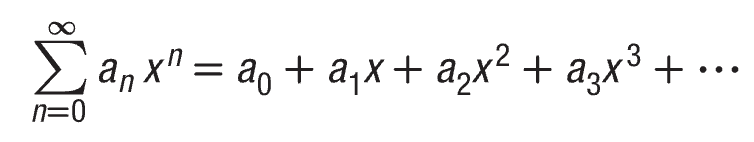
18
New cards
Exponential Series
* Infinite
* Represents eˣ
* Represents eˣ
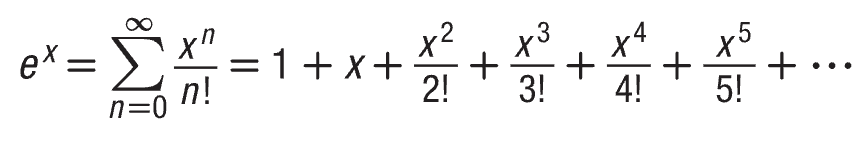
19
New cards
Power Series for cos x
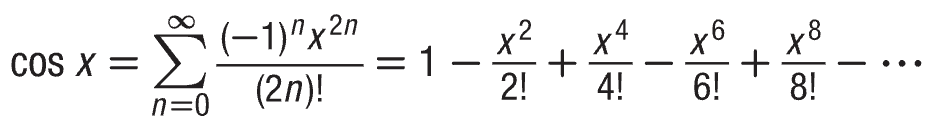
20
New cards
Power Series for sin x
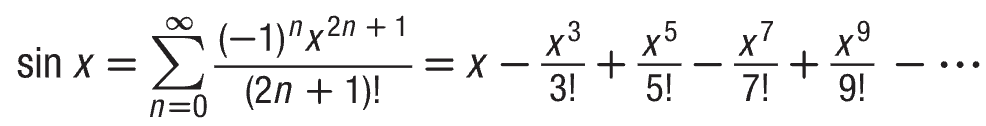
21
New cards
Euler’s Formula
eⁱᶿ = cos θ + i sin θ
22
New cards
Exponential Form of a Complex Number
a + bi = r × eⁱᶿ
* r = √(a² + b²)
* θ = tan⁻¹(b/a); a > 0
* θ = tan⁻¹(b/a) + π; a < 0
* r = √(a² + b²)
* θ = tan⁻¹(b/a); a > 0
* θ = tan⁻¹(b/a) + π; a < 0
23
New cards
Natural Logarithm of a Negative Number
iπ = ln (-1)
* ln (-k) = ln \[(k)(-1)\]
* ln (k) + ln (-1)
* ln k + iπ
* ln (-k) = ln \[(k)(-1)\]
* ln (k) + ln (-1)
* ln k + iπ