AP Calculus BC Review

sin(0)=

sin(π/4)

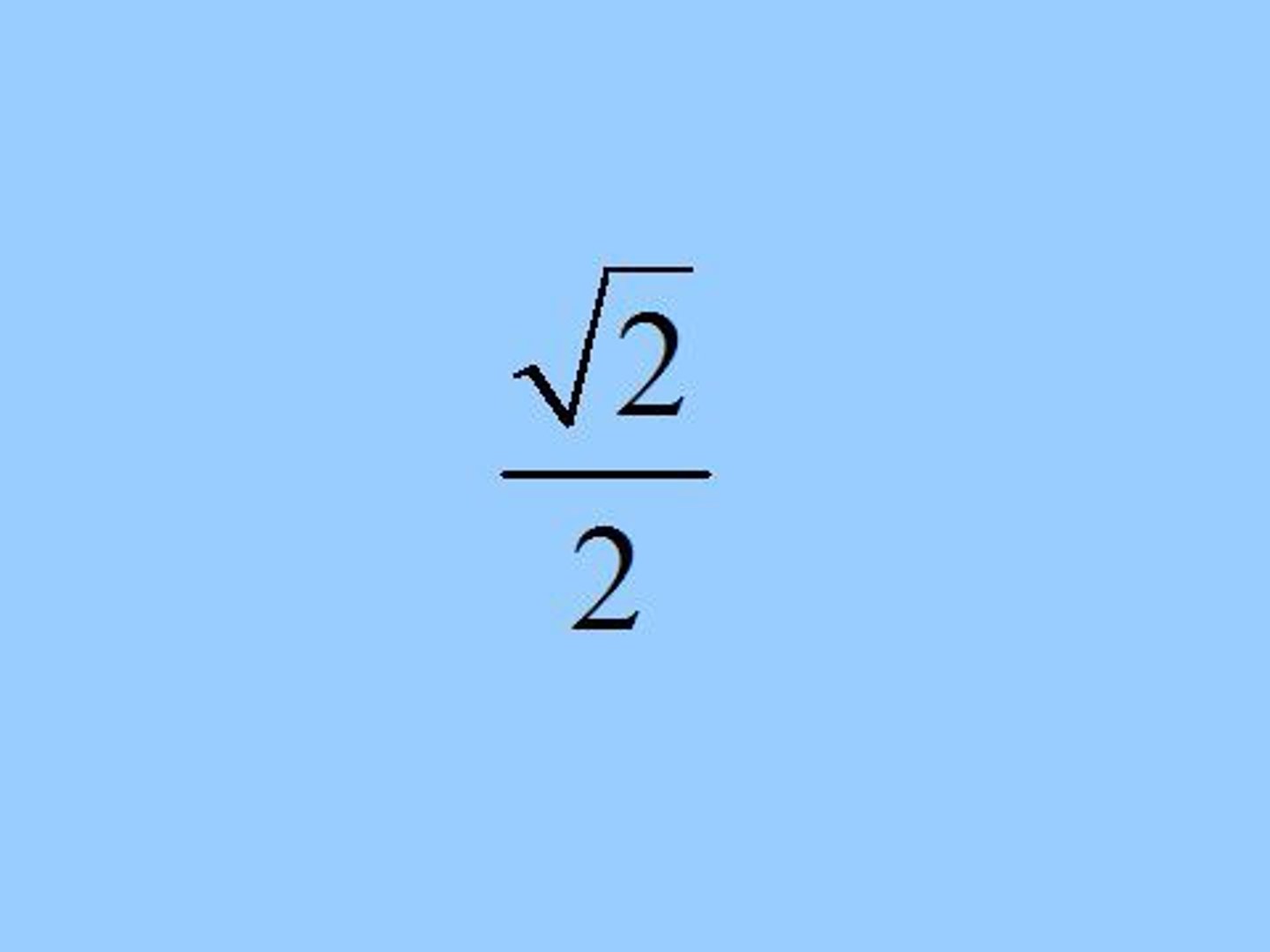
arcsin(-1)

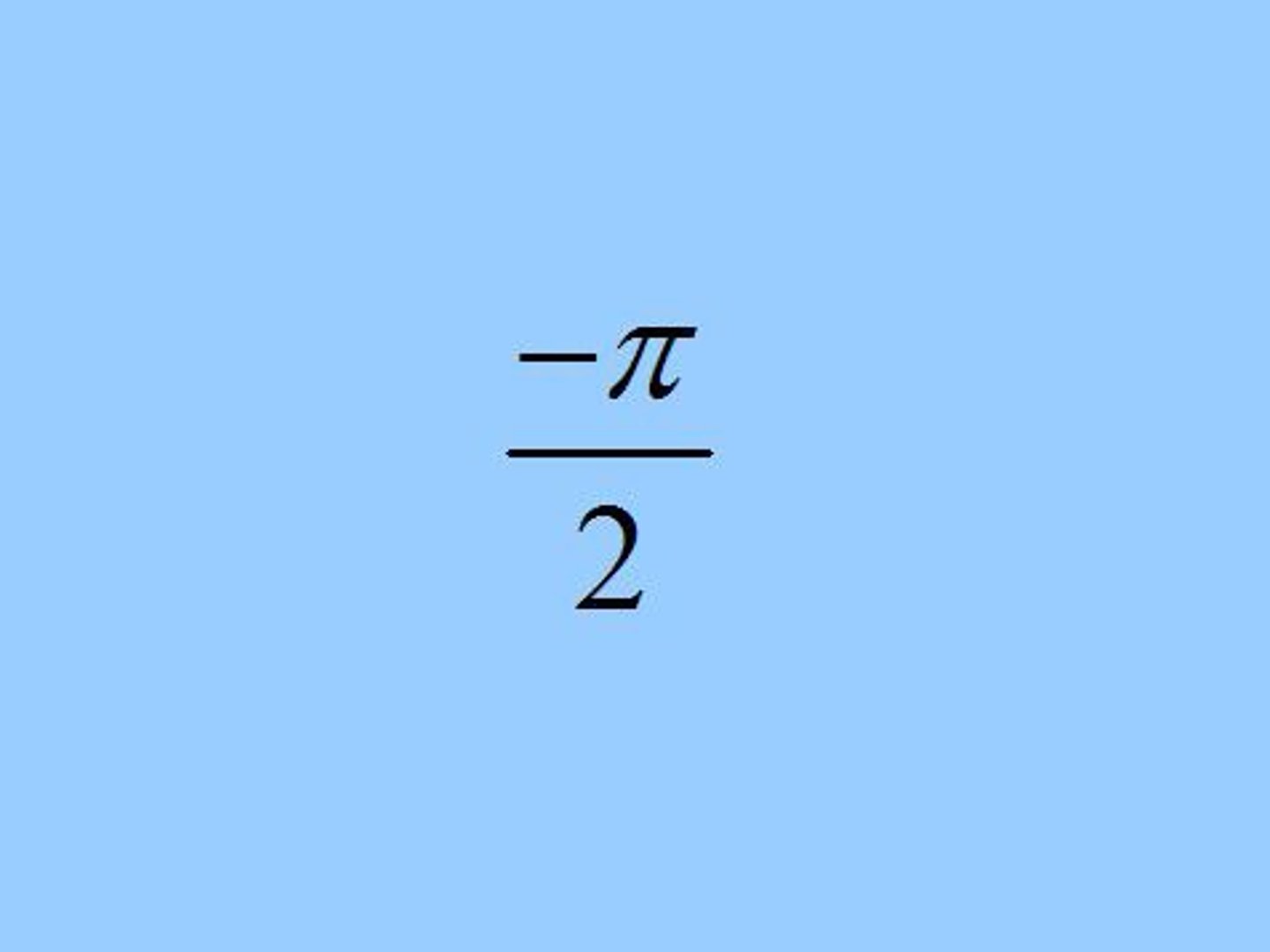
arctan(-1)

log(AB)

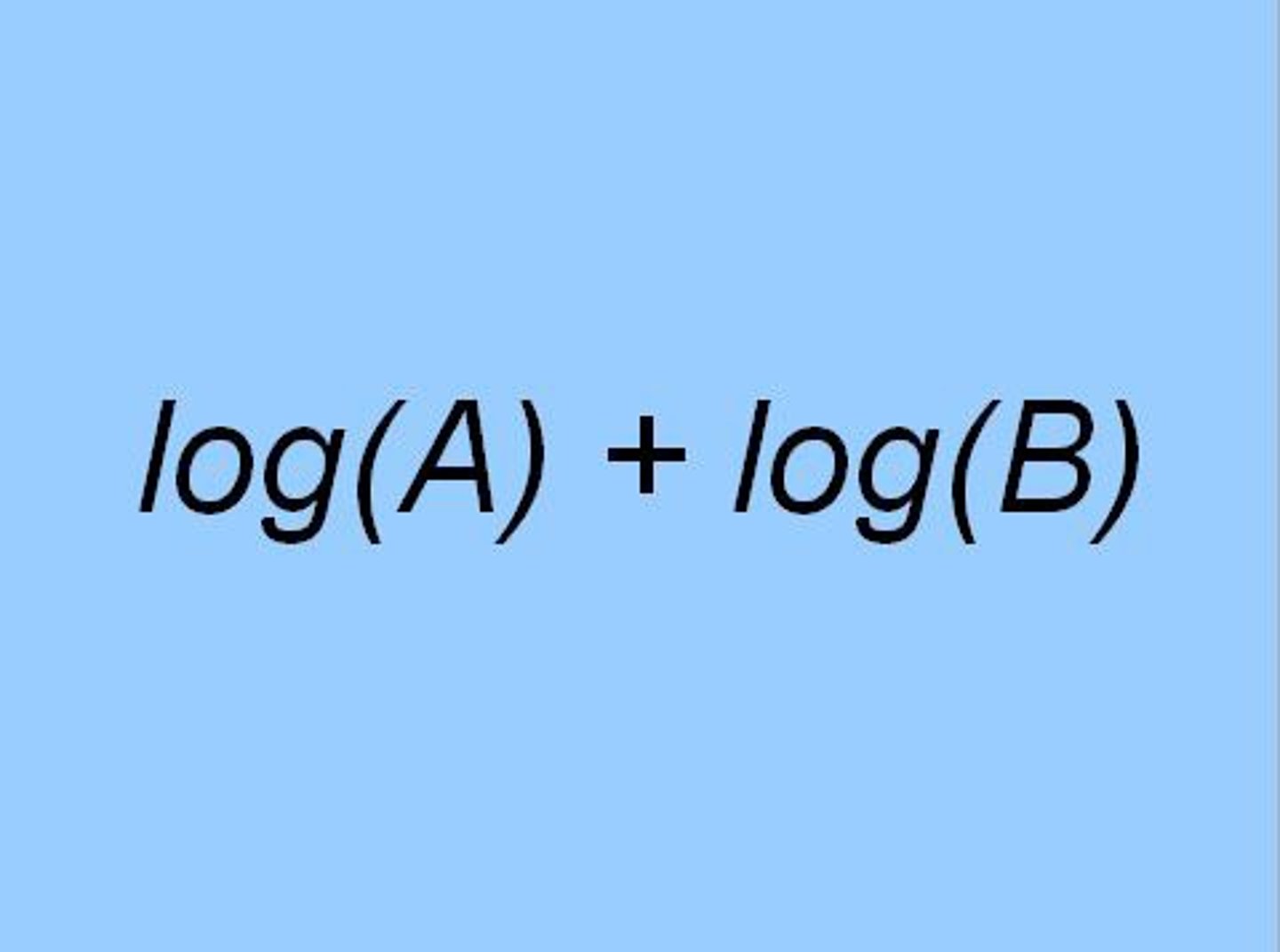
log(A / B)

log(A) ^ x

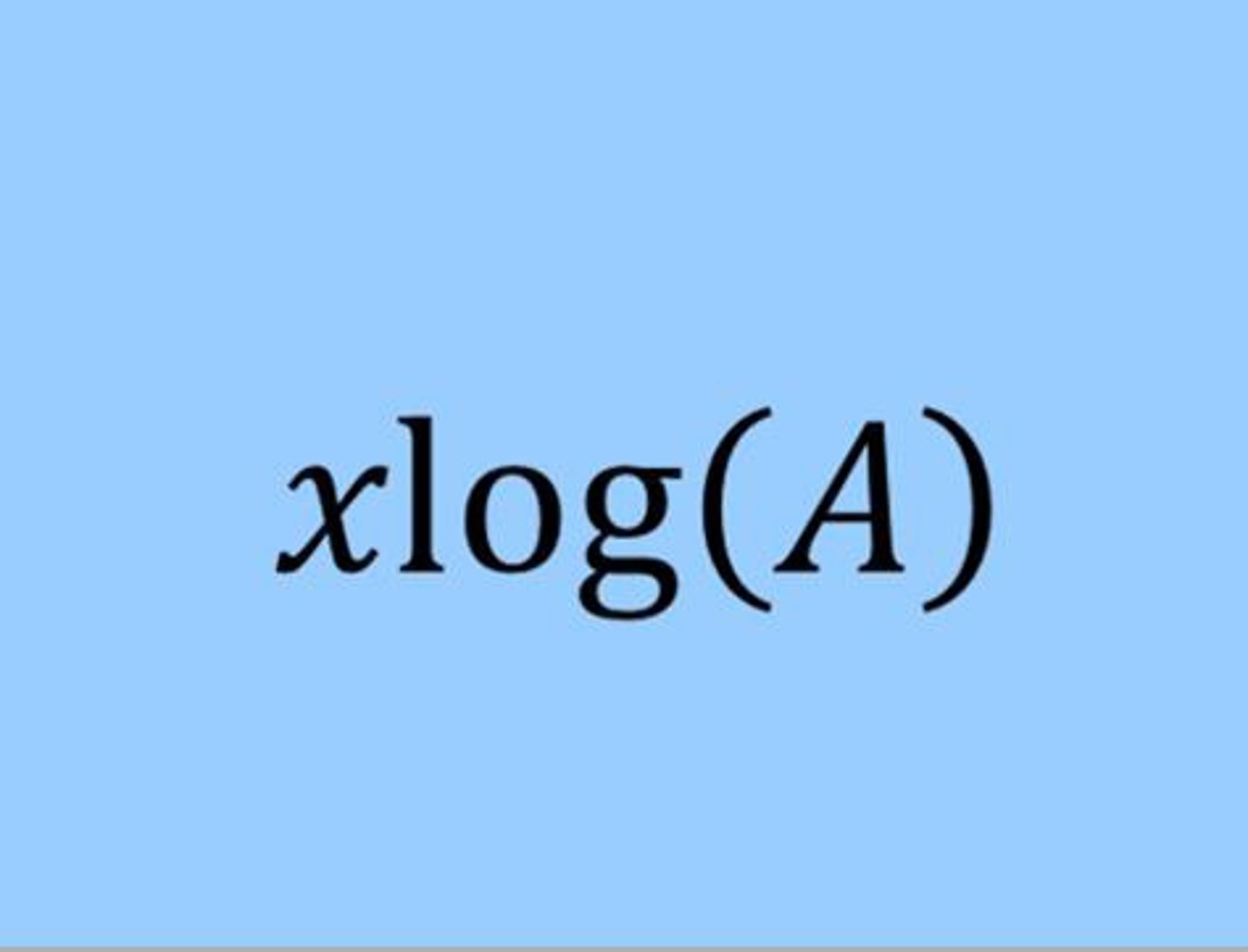
e^(ln(x))

For what value of x is there a

hole, and for what value of x

is there a vertical asymptote?

f(x) = ((x - a)(x - b))/ ((x - a)(x - c))

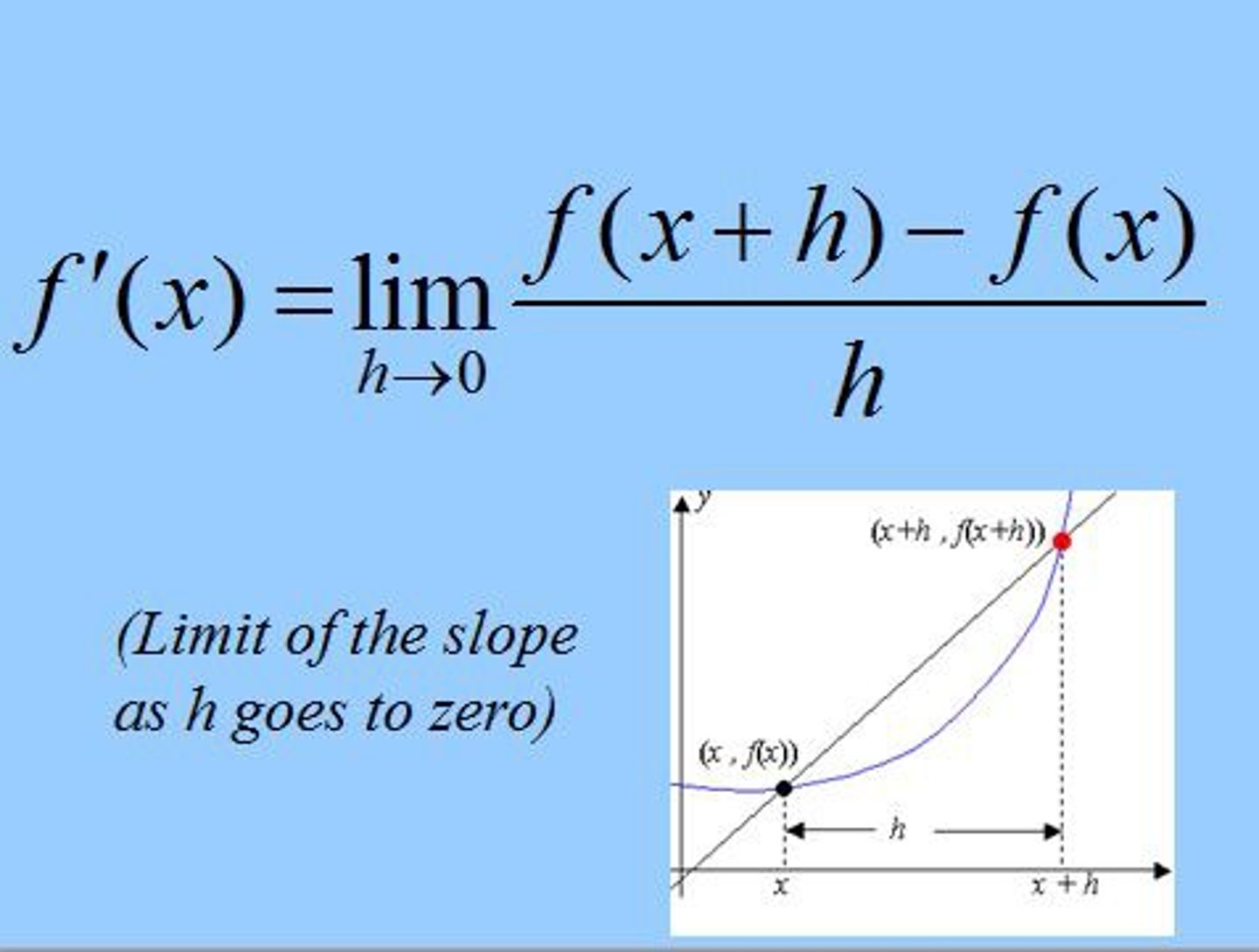
Definition of the Derivative

(Using the limit as h→0)

lim x→₀ sin(x)/x

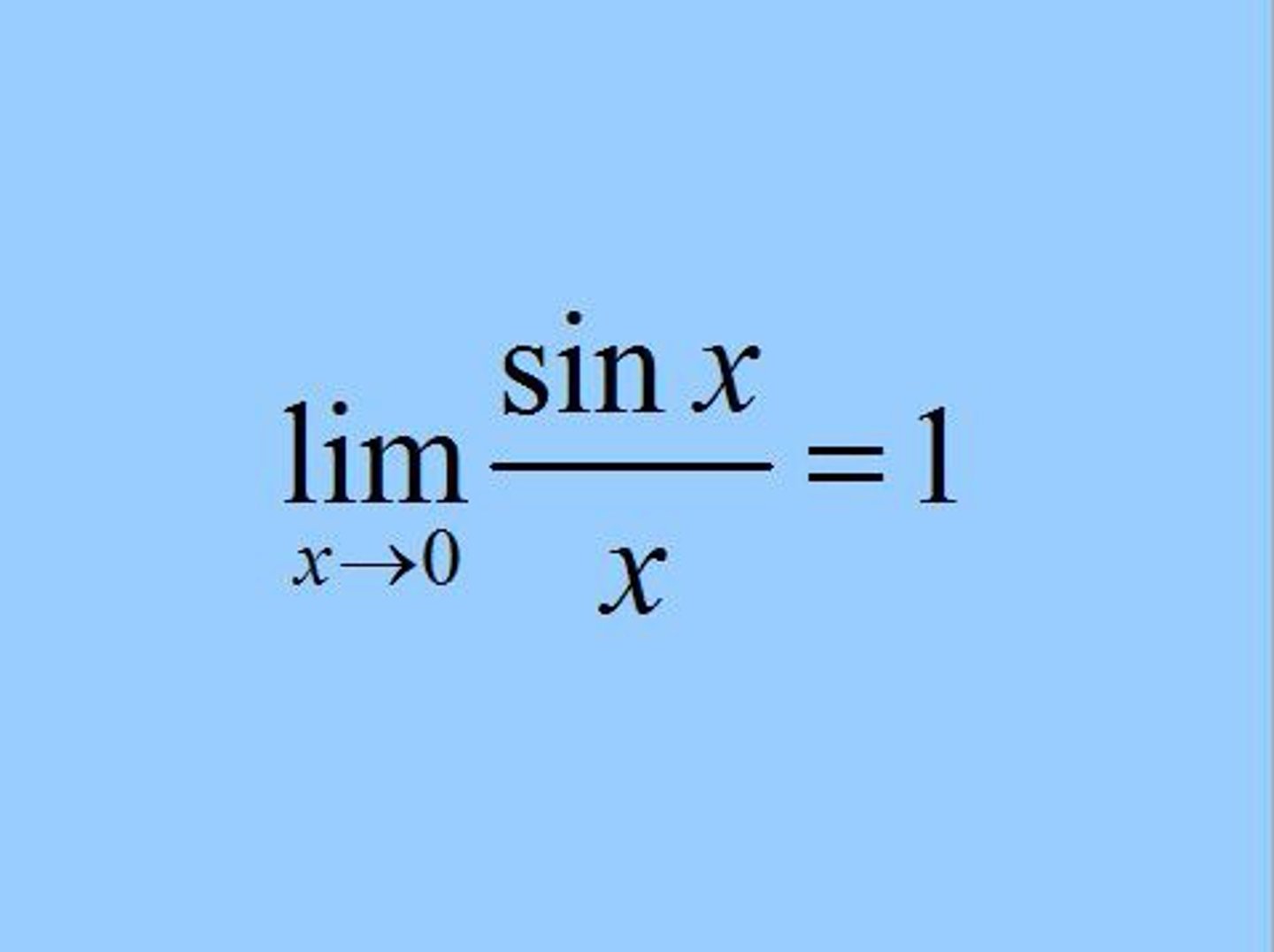
lim x→∞ arctanx

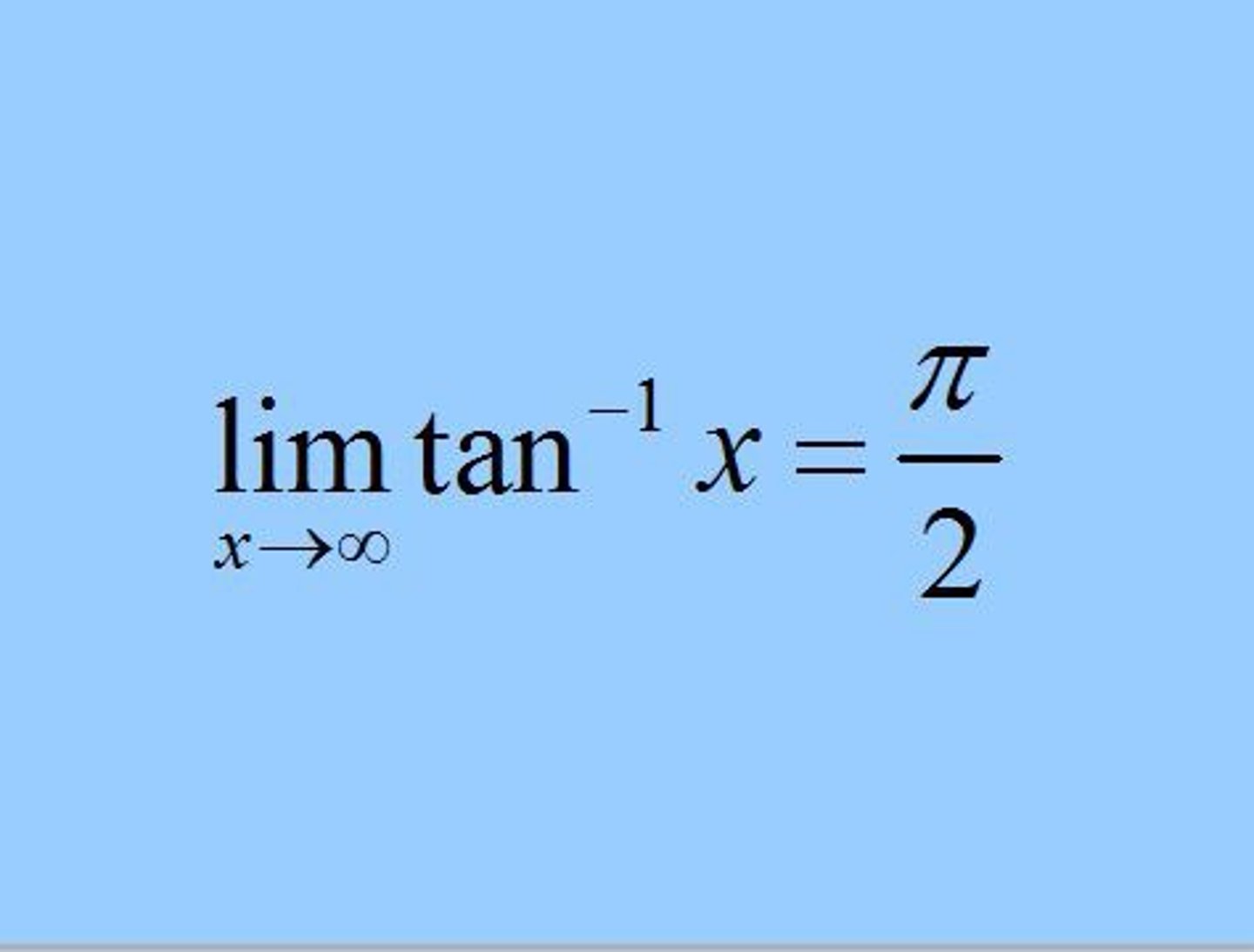
First derivative test for a local max of f at x = a

First derivative test for a local min of f at x = a

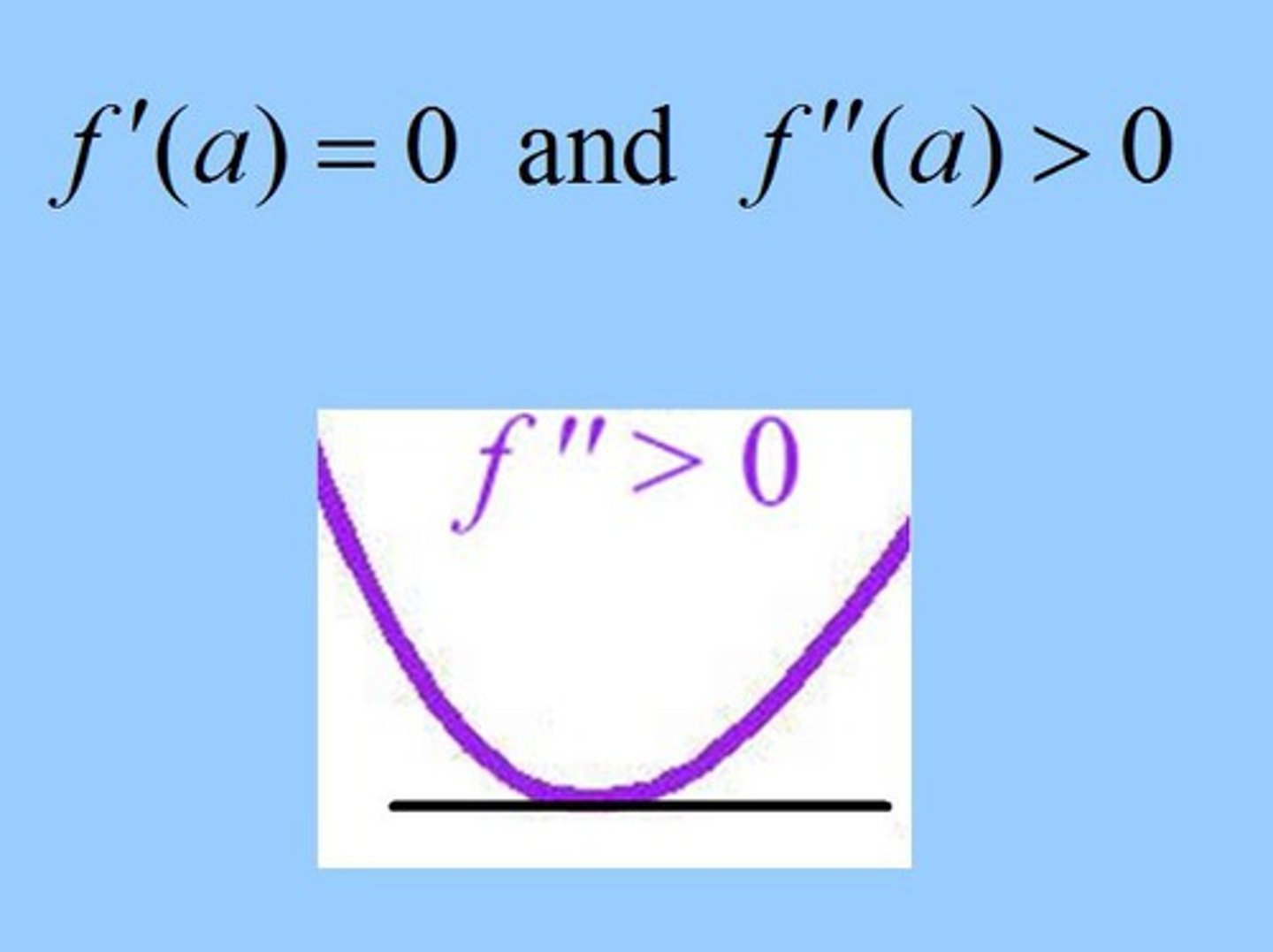
Second derivative test for a local max of f at x = a

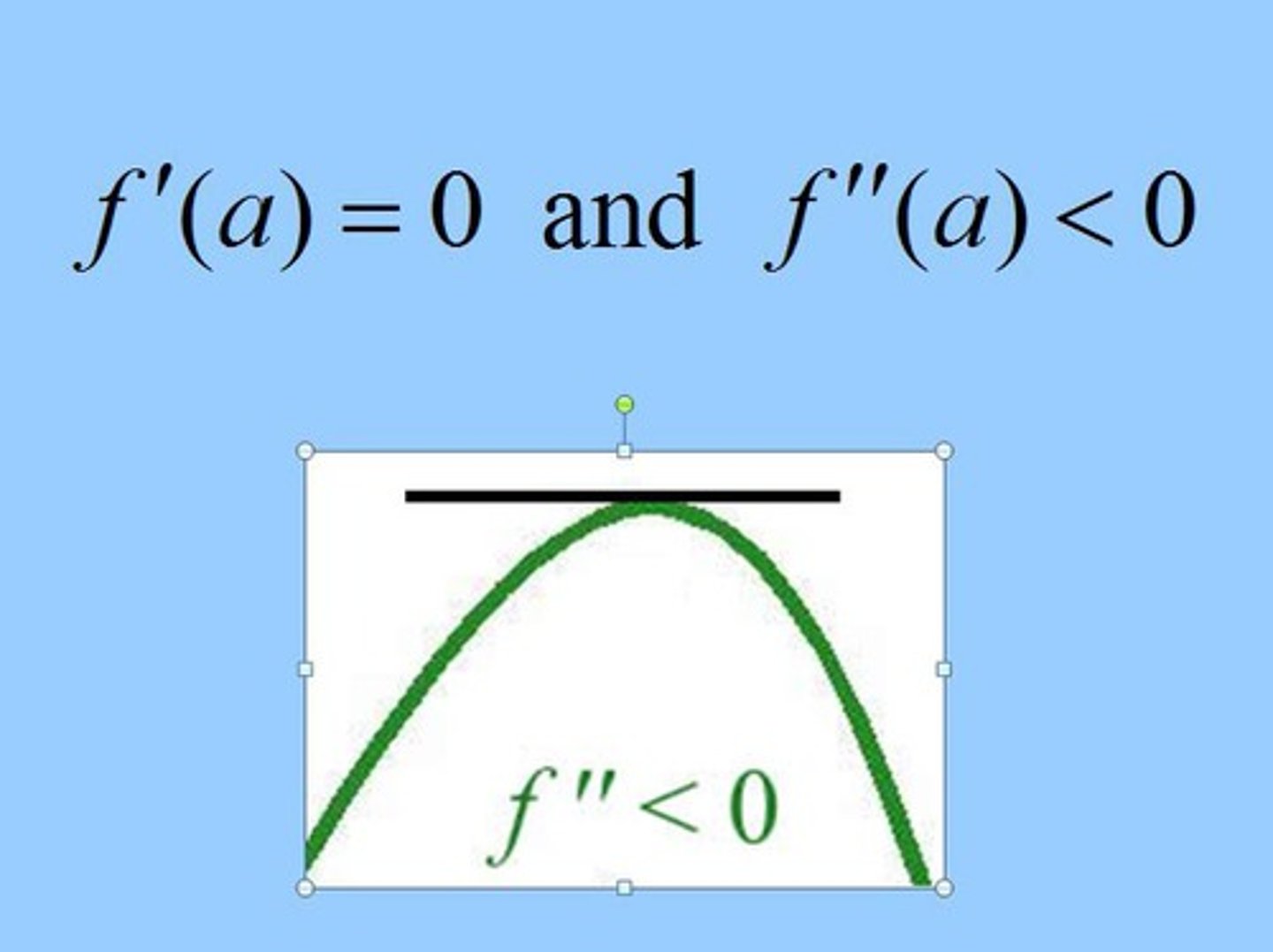
Second derivative test for a local min of f at x = a

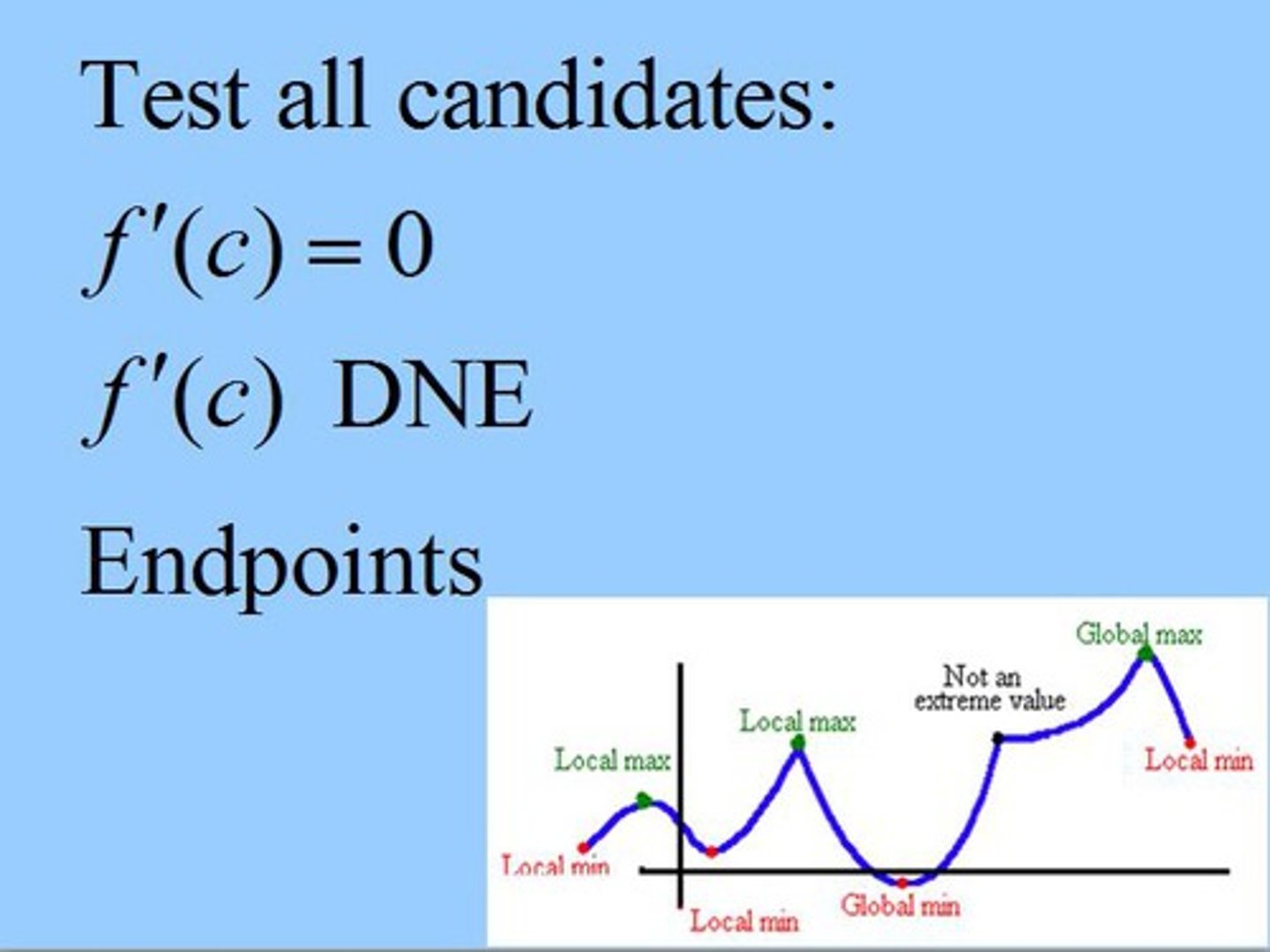
Test for max and mins of f on [a, b]

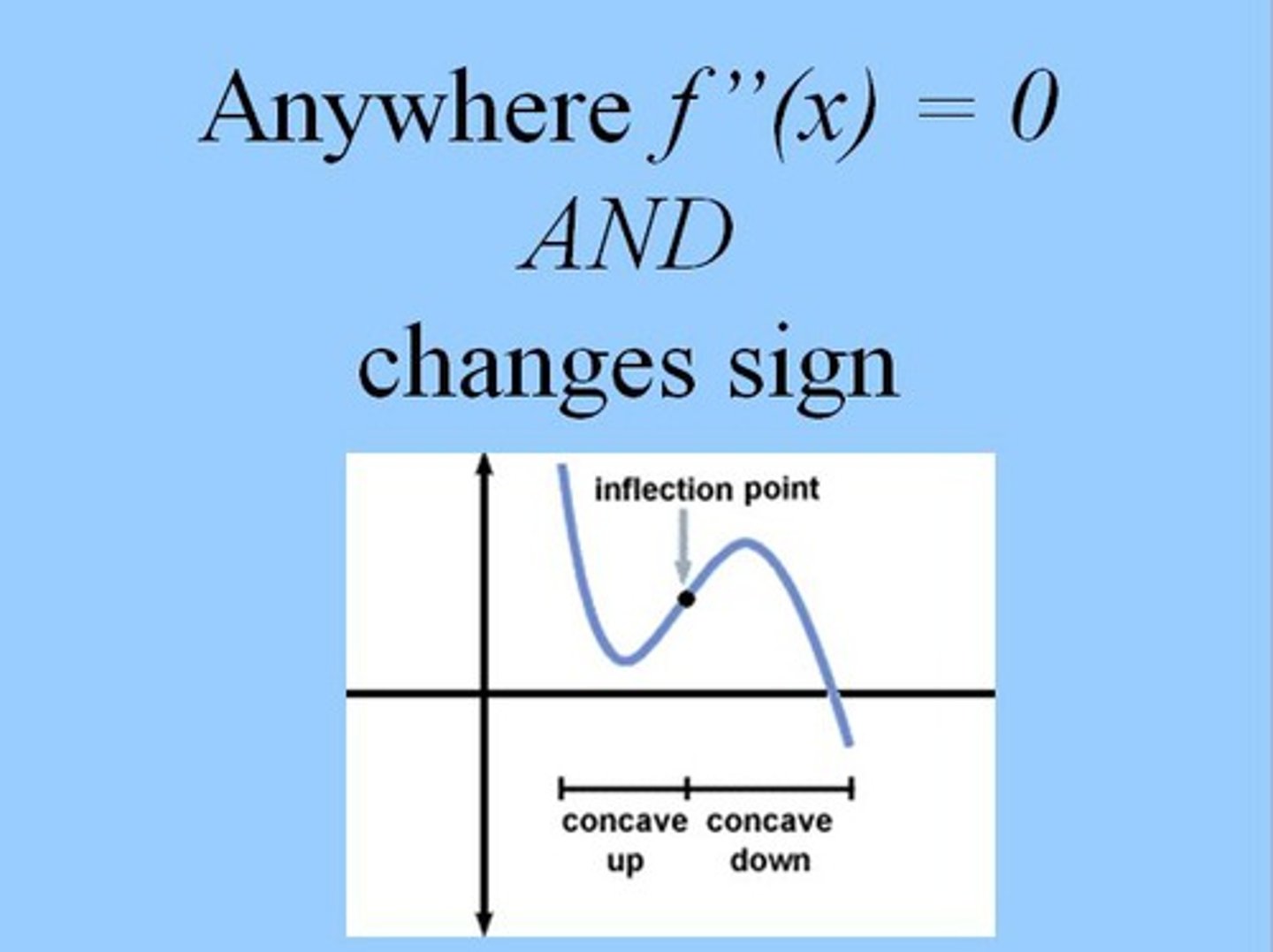
Inflection Points

ƒ'(x) < 0

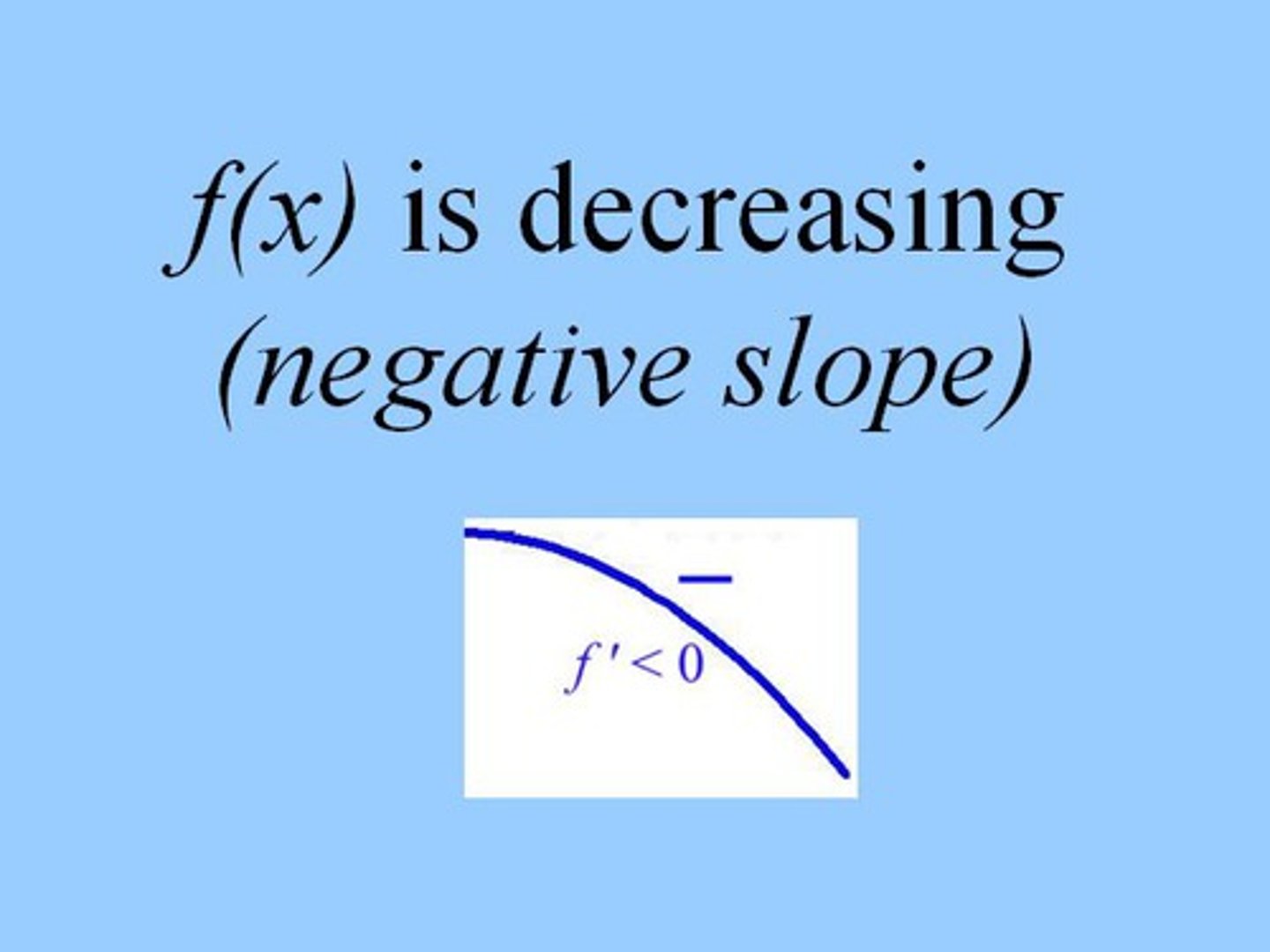
ƒ''(x) < 0 or ƒ'(x) is decreasing

ƒ'(x) > 0

ƒ''(x) > 0 or ƒ'(x) is increasing

Intermediate Value Theorem (IVT)

Mean Value Theorem (MVT)

ƒ(x) is continuous at x = a if...

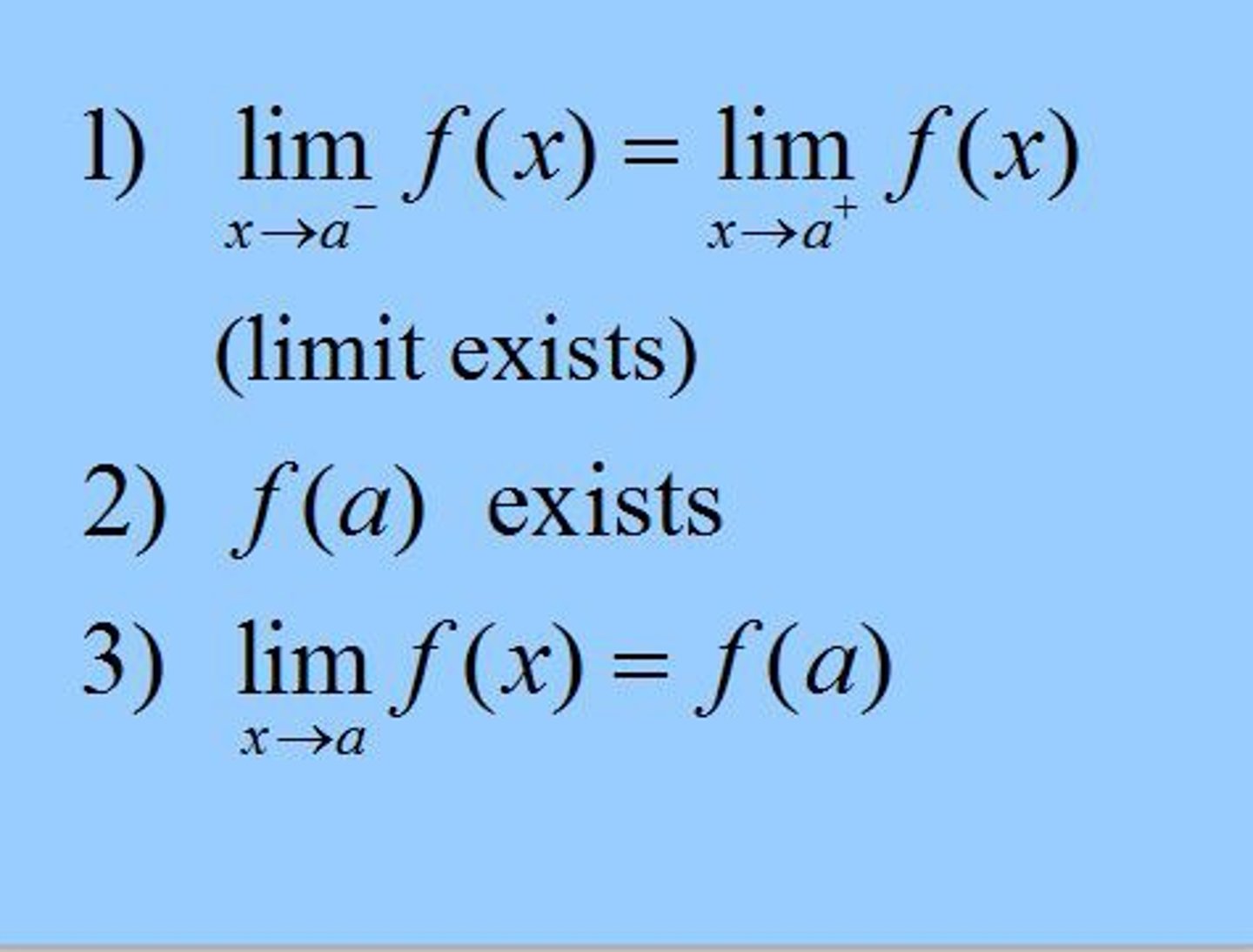
Extreme Value Theorem

Critical Points

Three types of discontinuities.

ƒ(x) is differentiable at x = a if...

Three conditions where ƒ(x) is not differentiable

Average rate of change of ƒ(x) over [a, b]

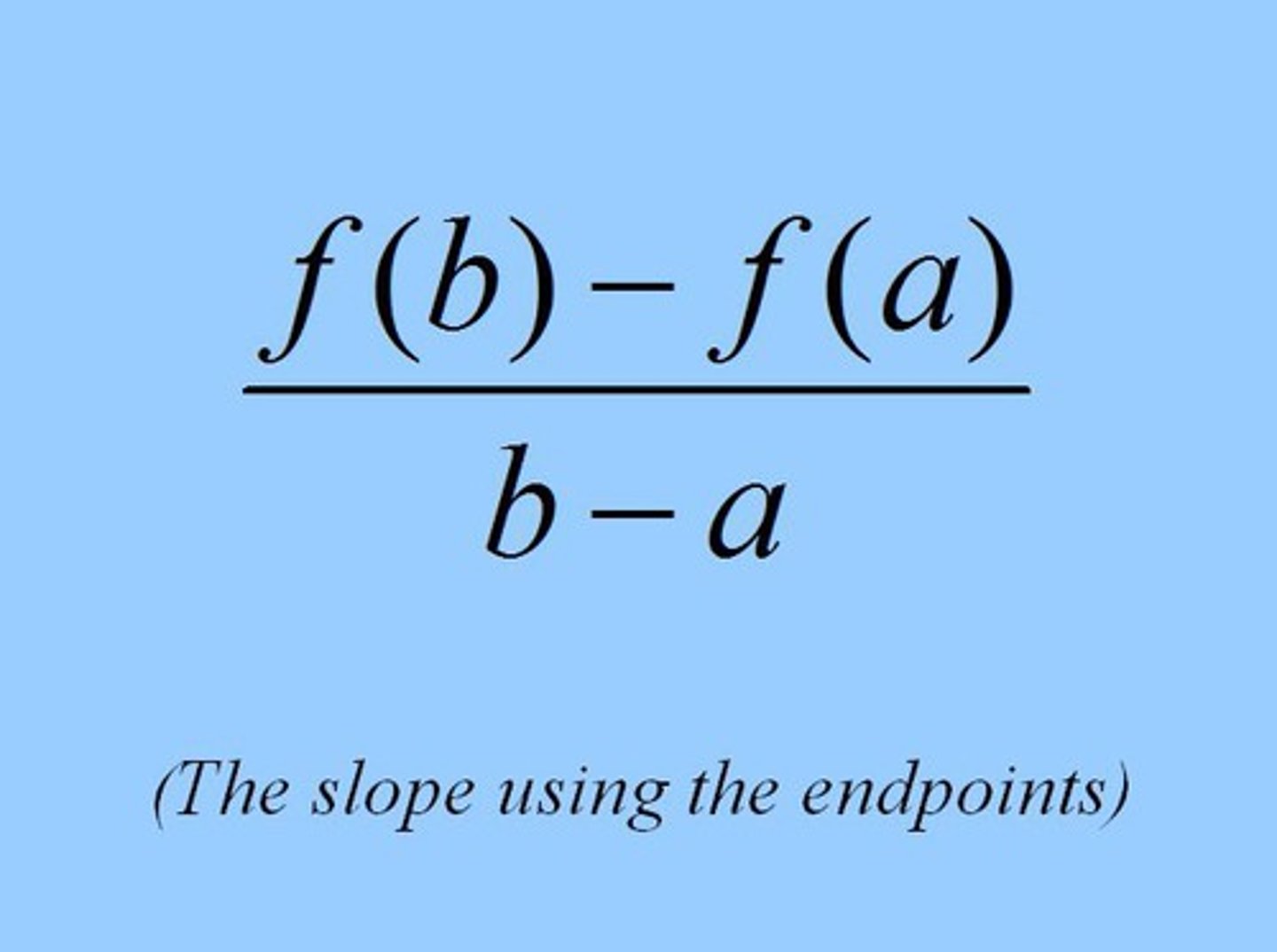
Instantaneous rate of change of ƒ(a)

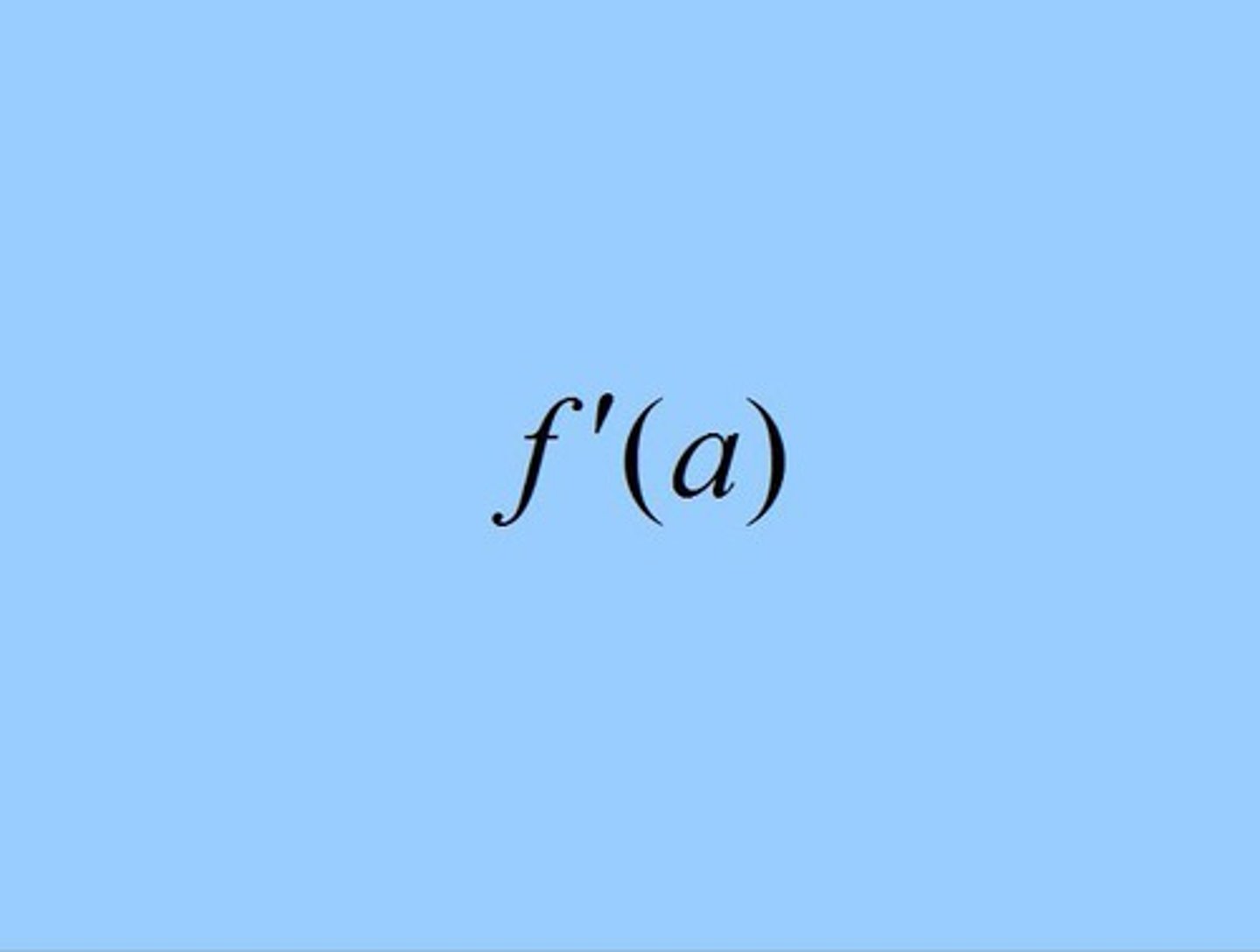
d/dx ( arctan ( x ) )

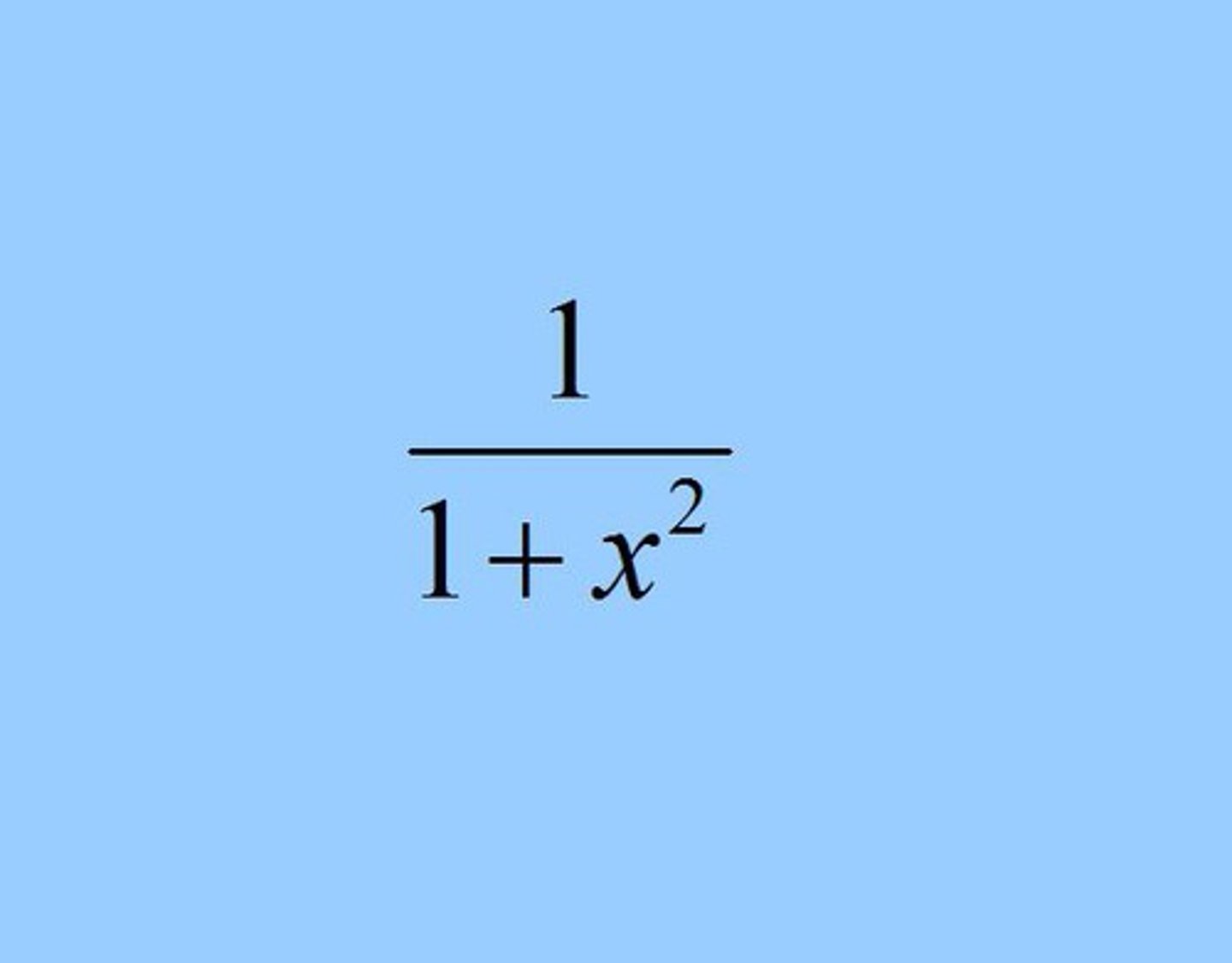
d/dx ( arcsin ( x ) )

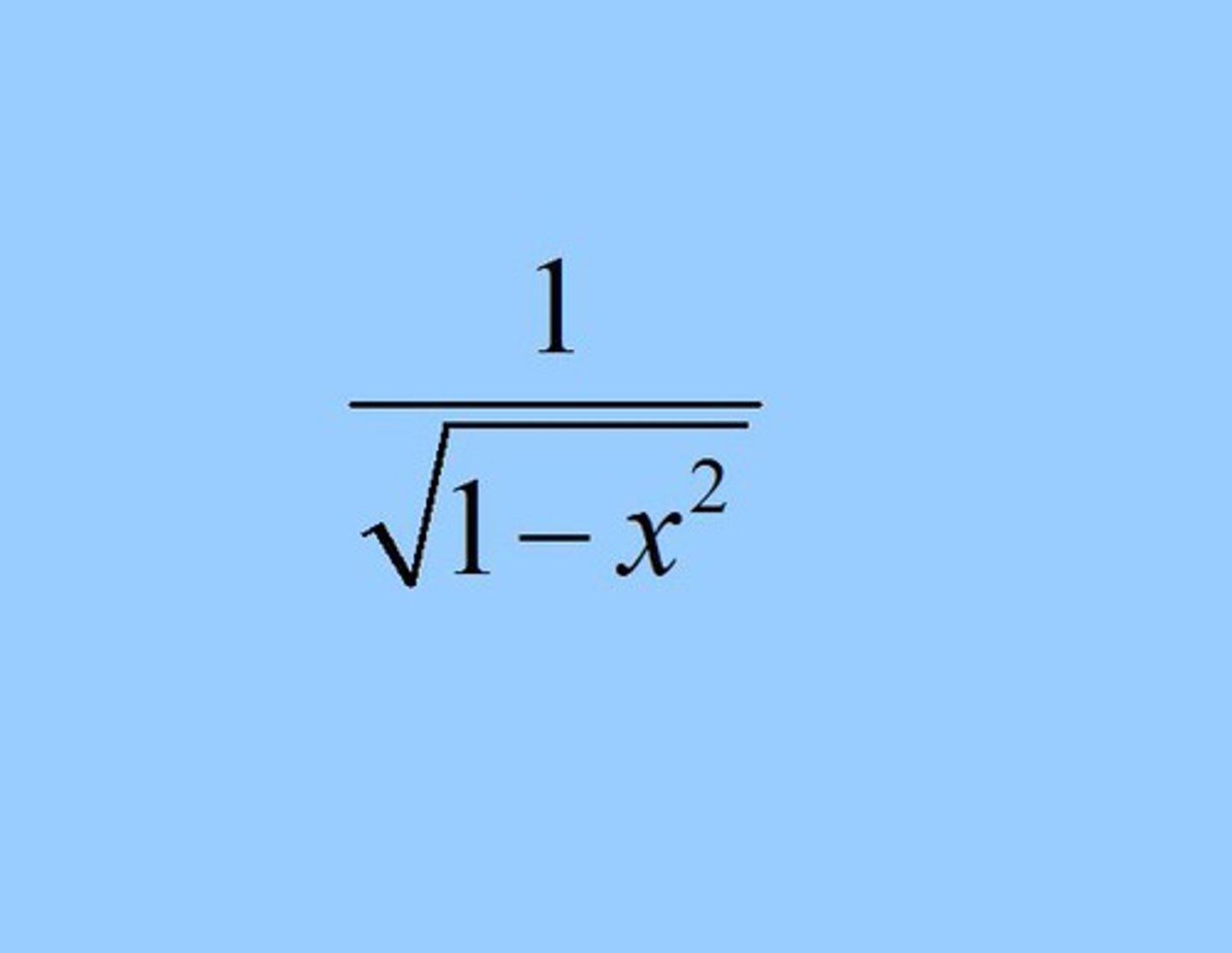
d/dx ( e ^ x )

d/dx ( ln x )

d/dx ( a ^ x )

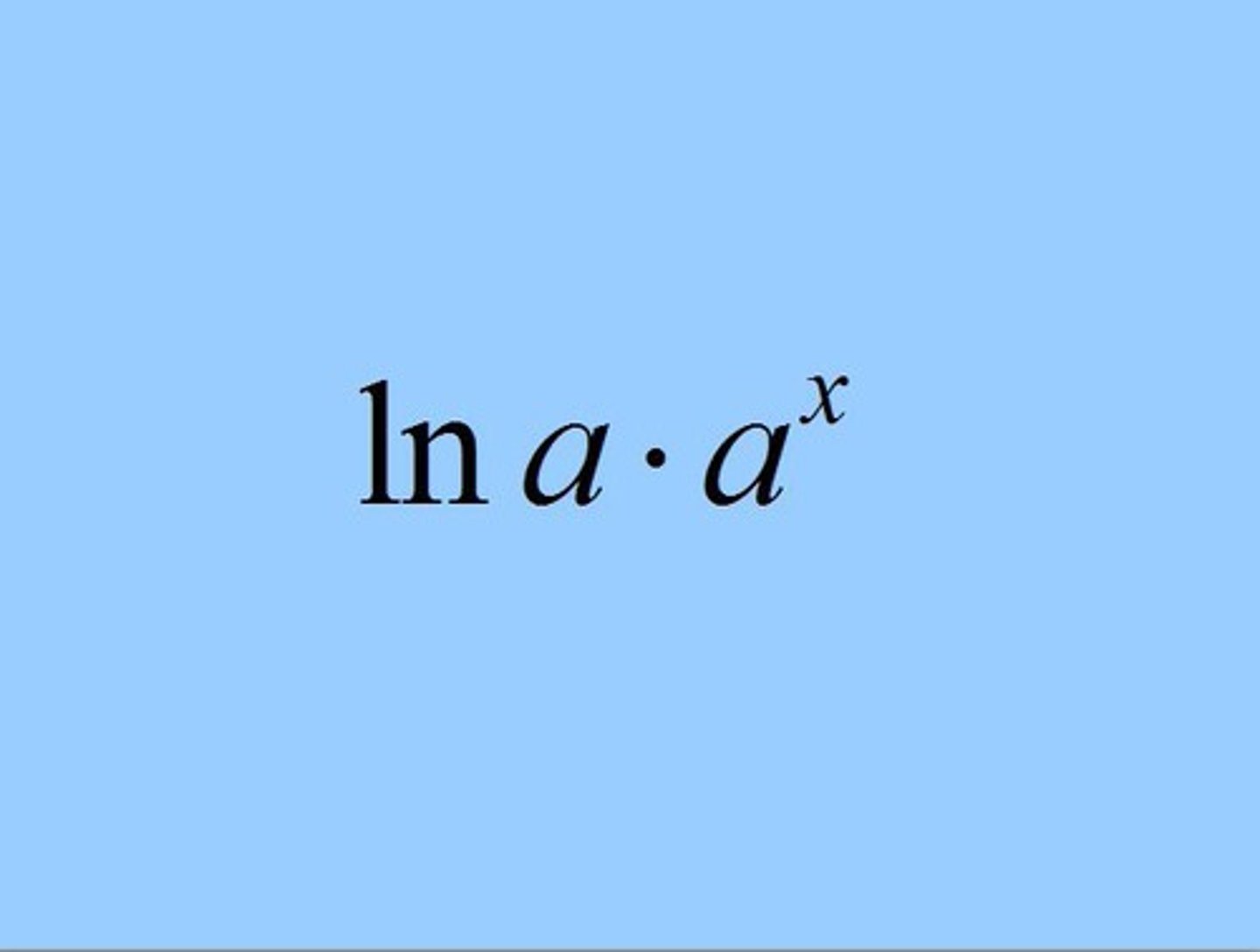
d/dx ( sin x )

d/dx ( cos x )

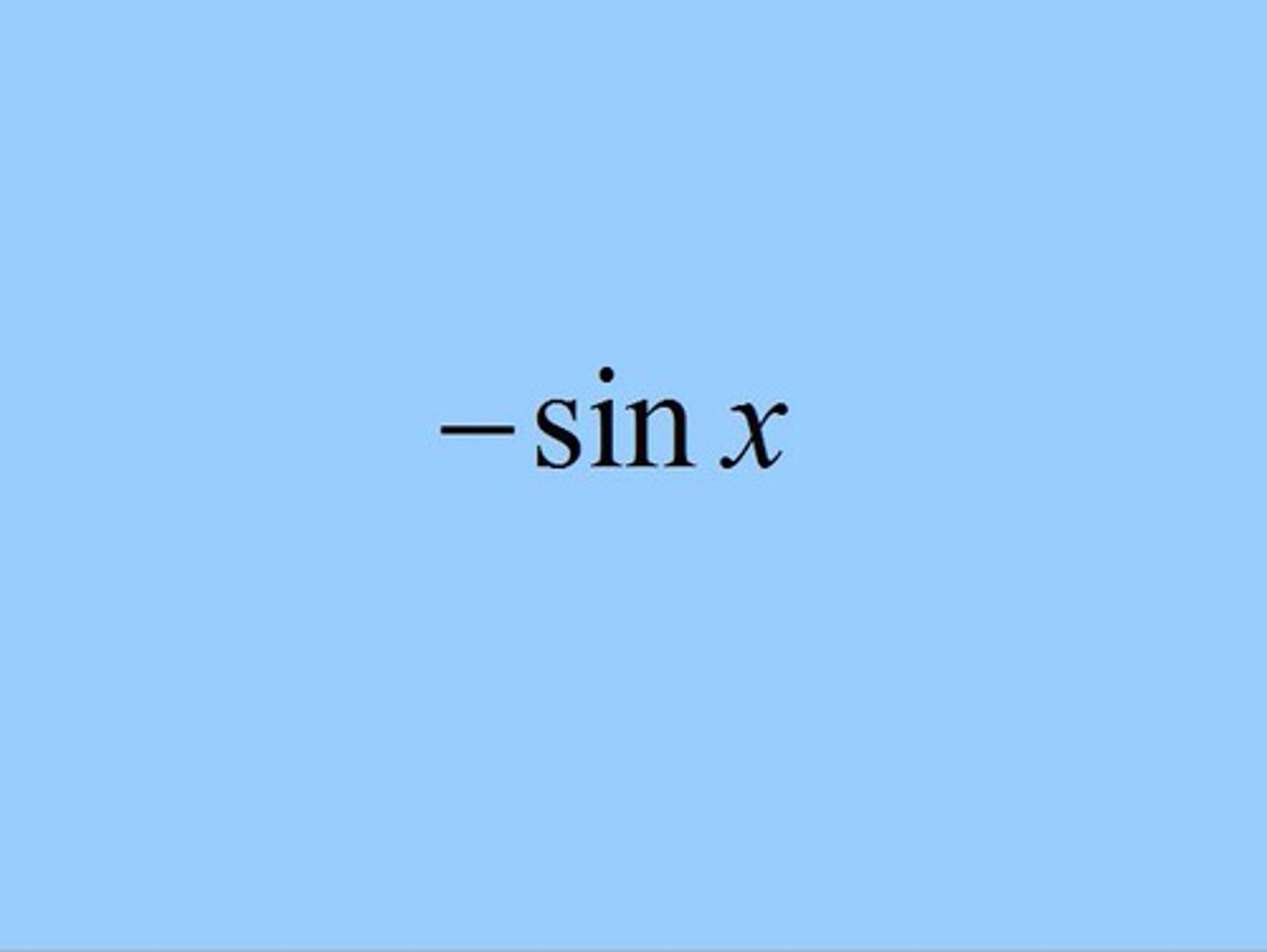
d/dx ( tan x )

Product Rule

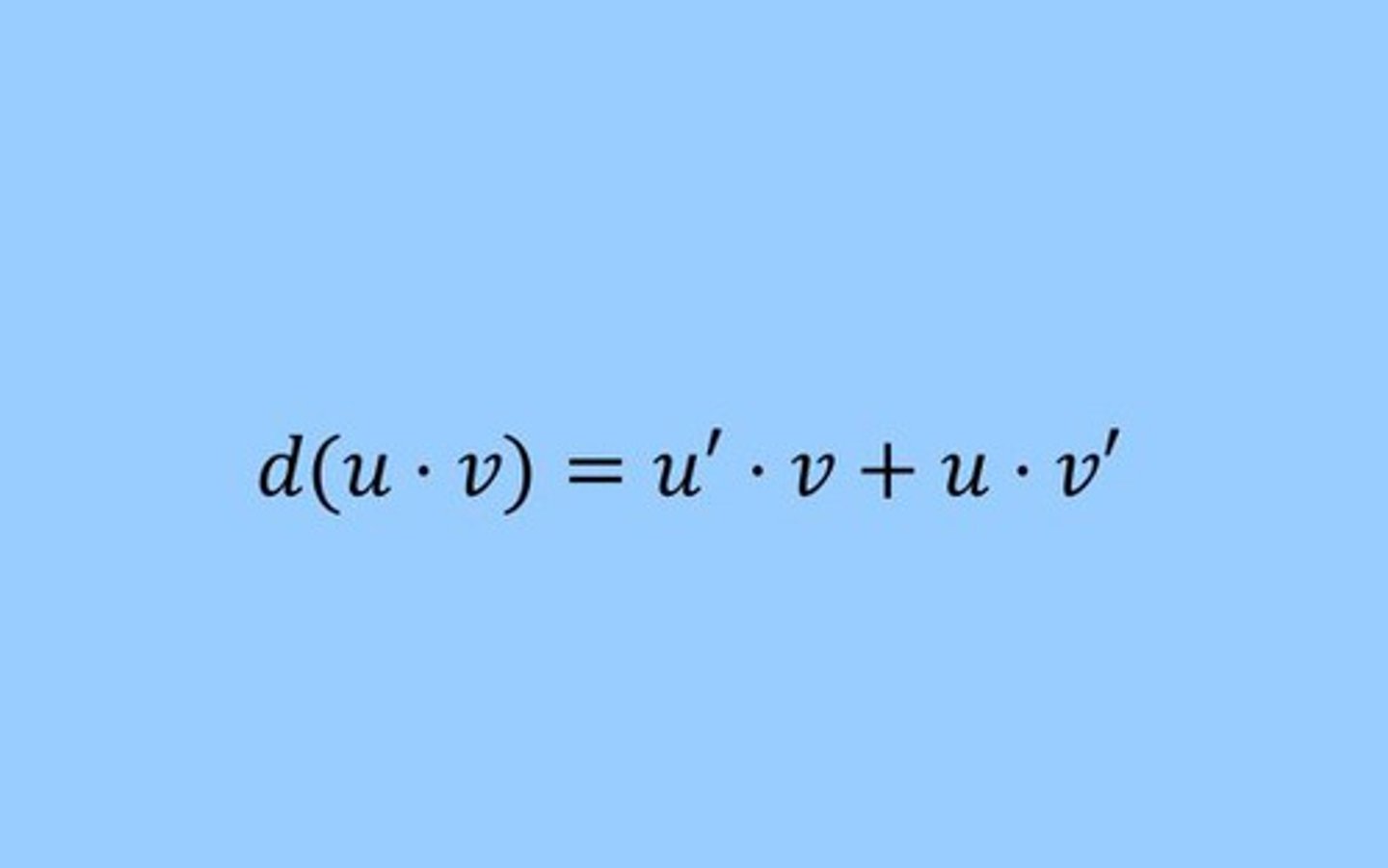
Quotient Rule

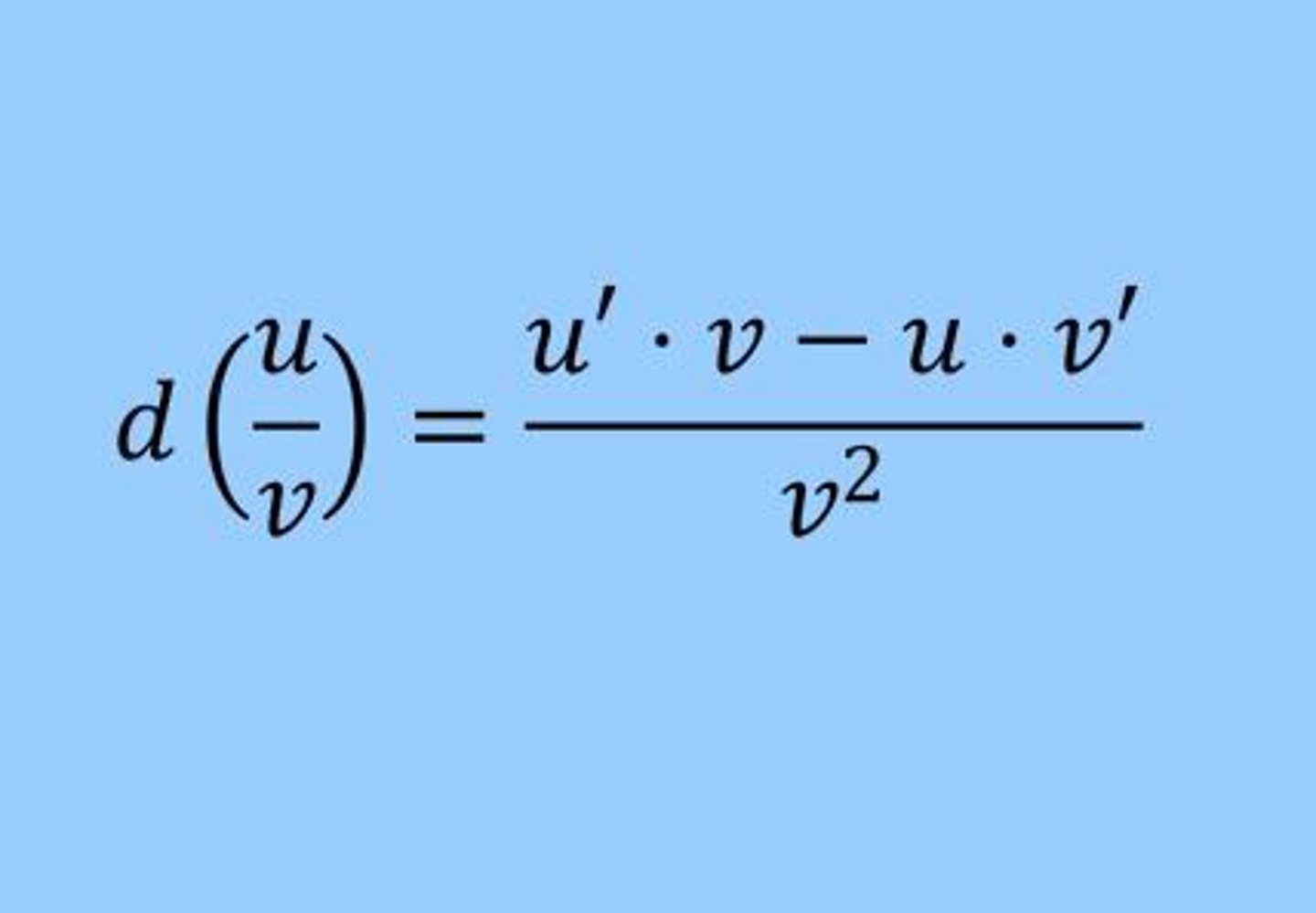
Chain Rule

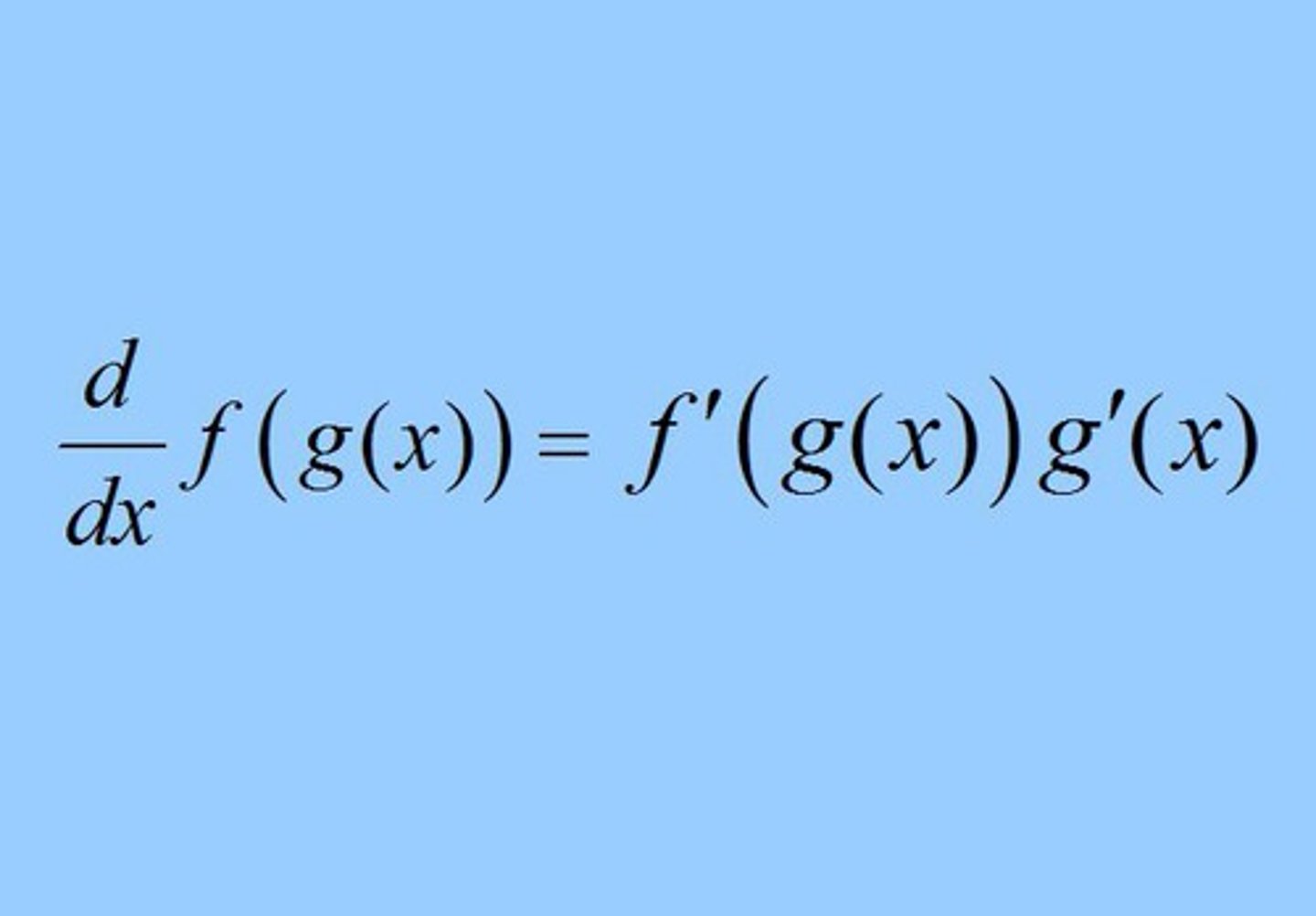
d/dx (ƒ(x)³)

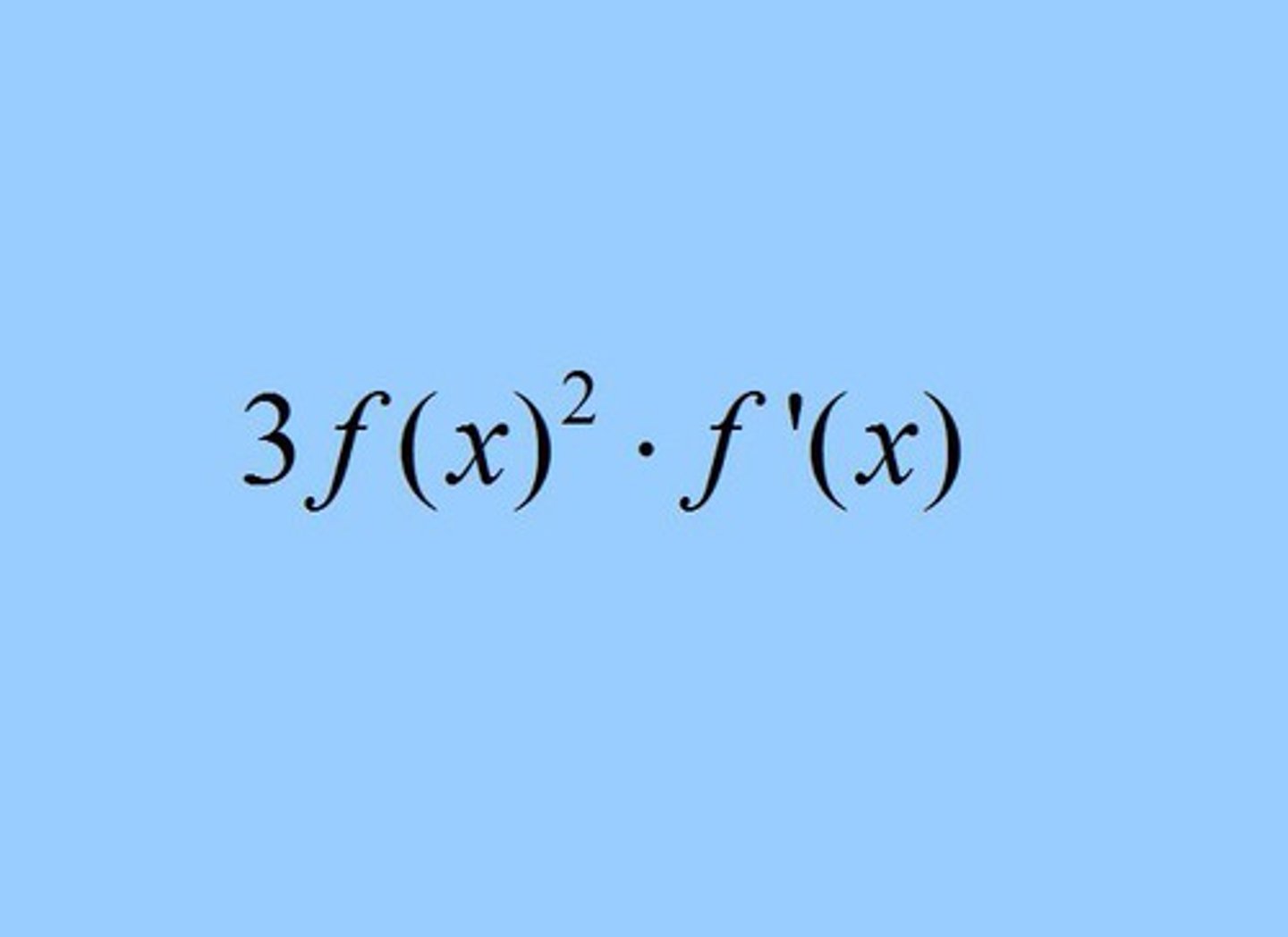
d/dx ( ln ƒ(x) )

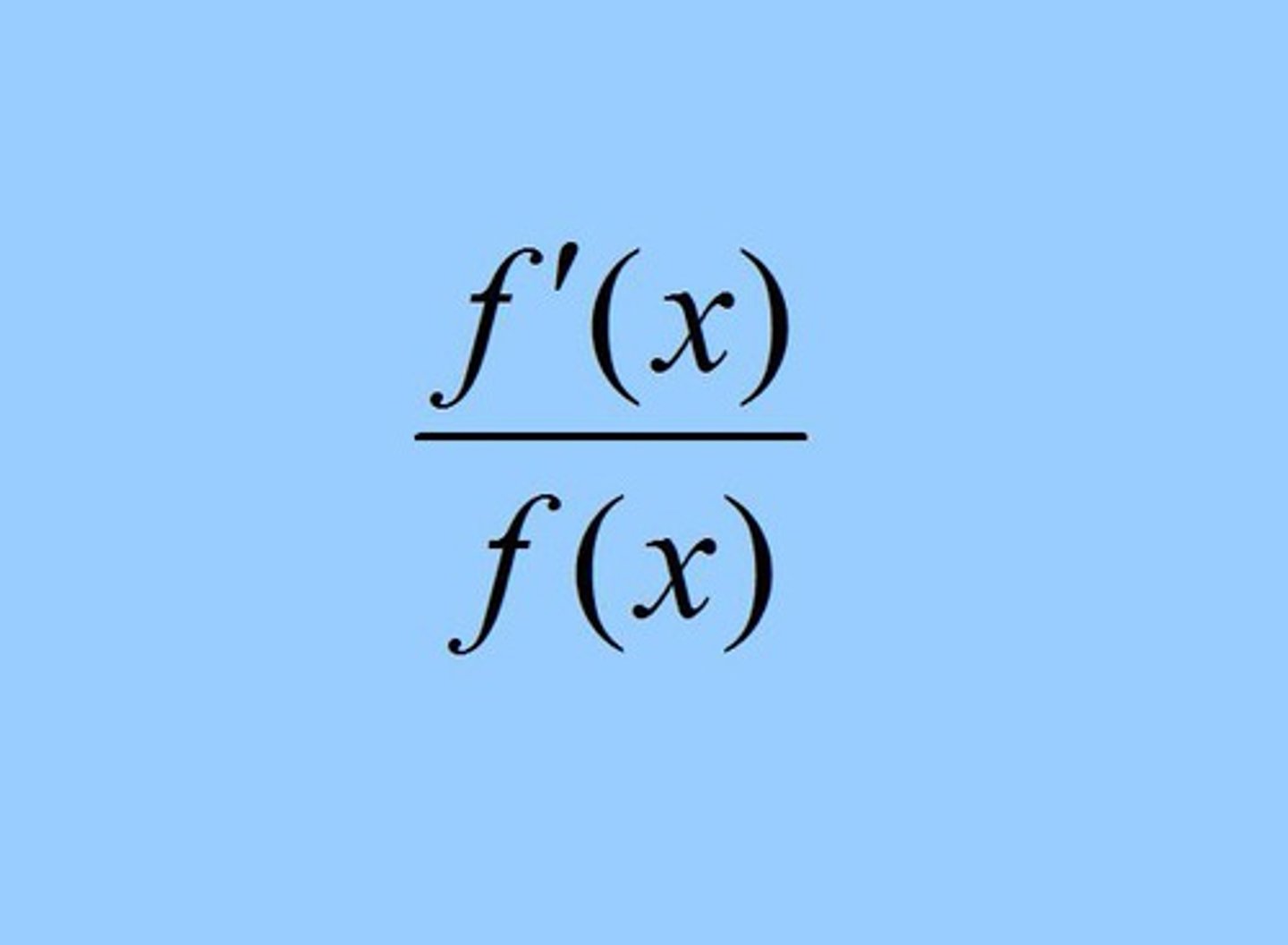
d/dx (e ^ ƒ(x) )

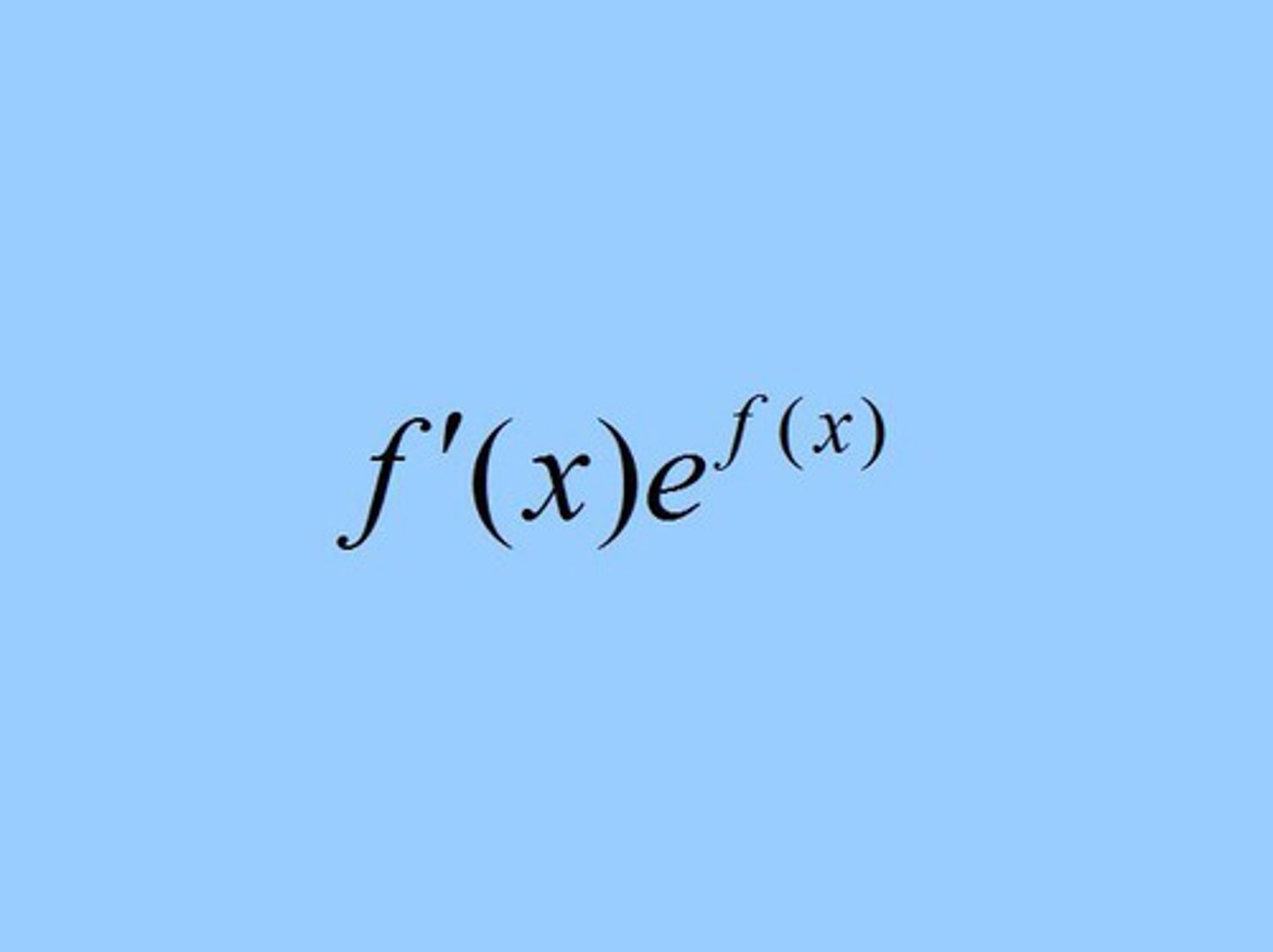
Derivative of the Inverse of ƒ(x)

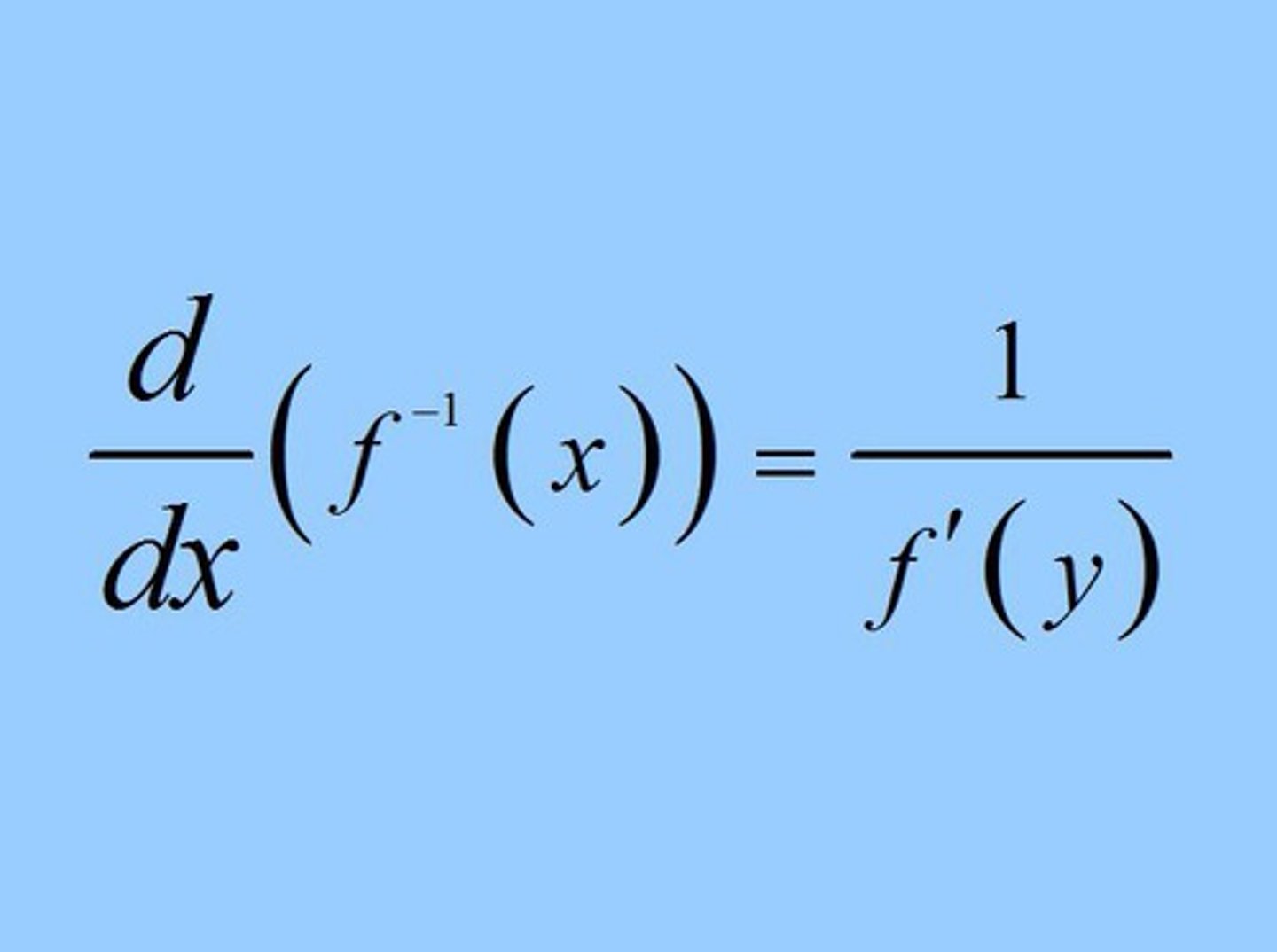
Implicit Differentiation

Find dy/dx:

x²/9+y²/4=1

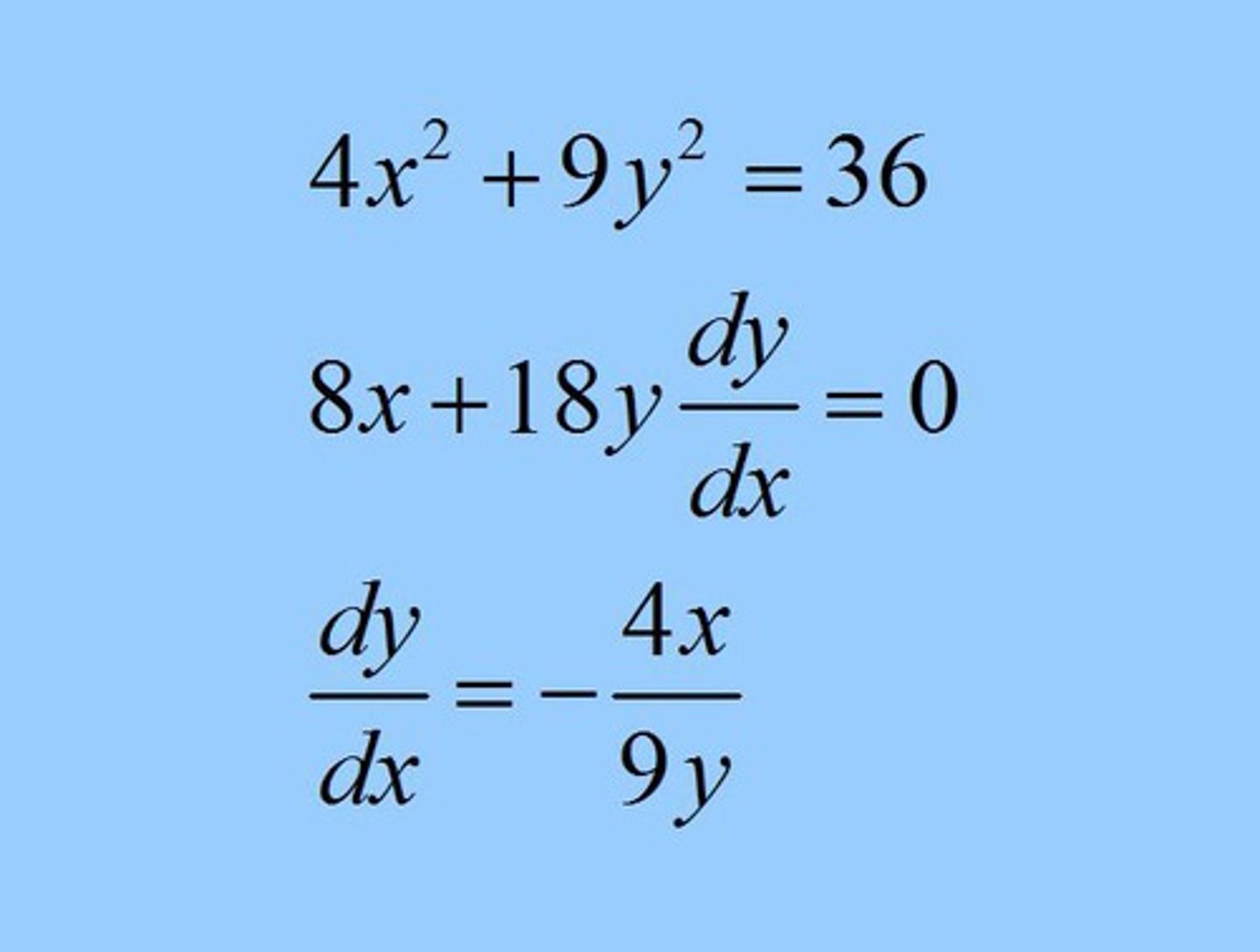
Equation of the tangent line

to y = ƒ(x)

at x = a

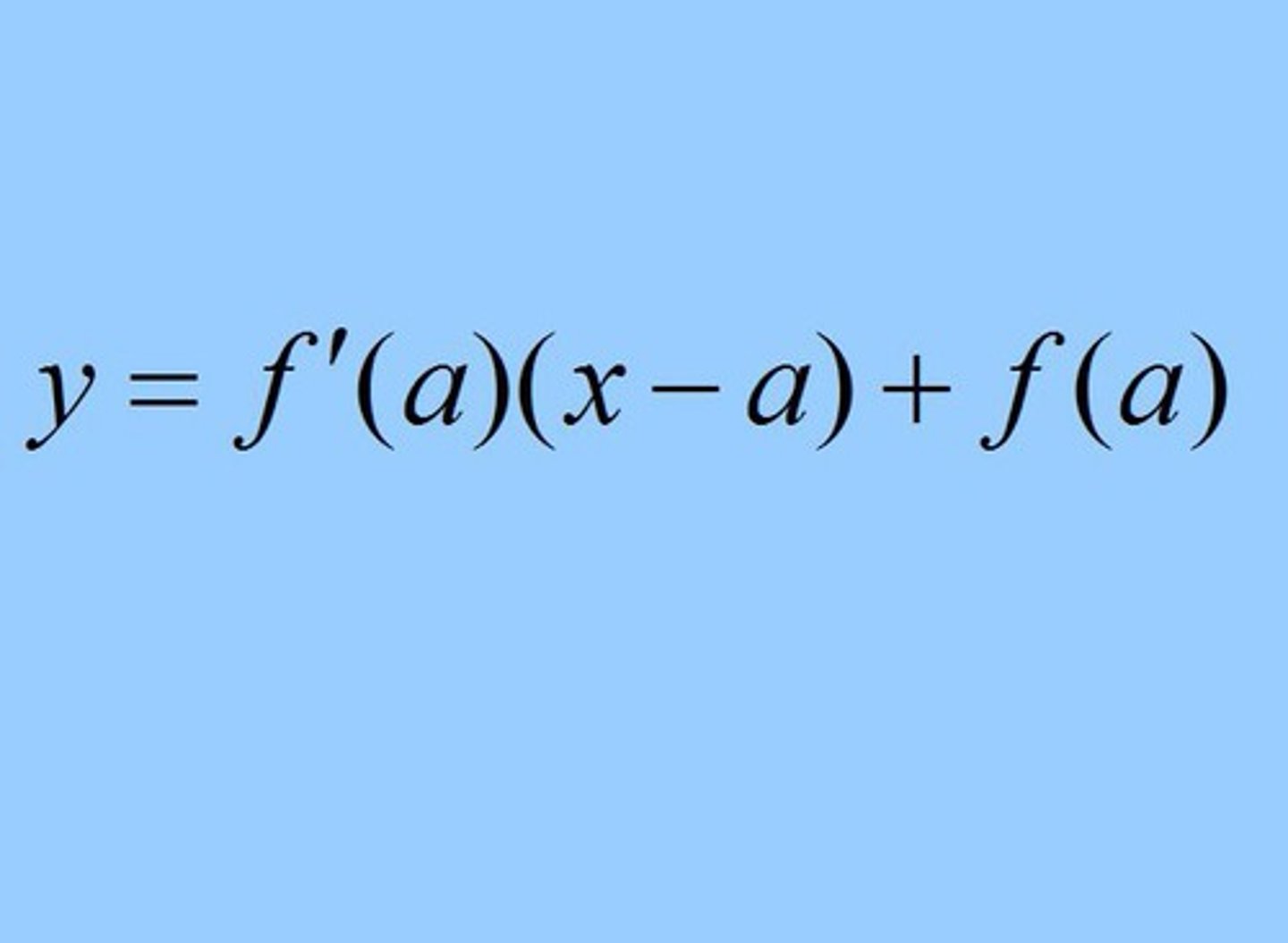
A normal line to a curve is...

Velocity of a point moving along a line with position at time t given by d(t)

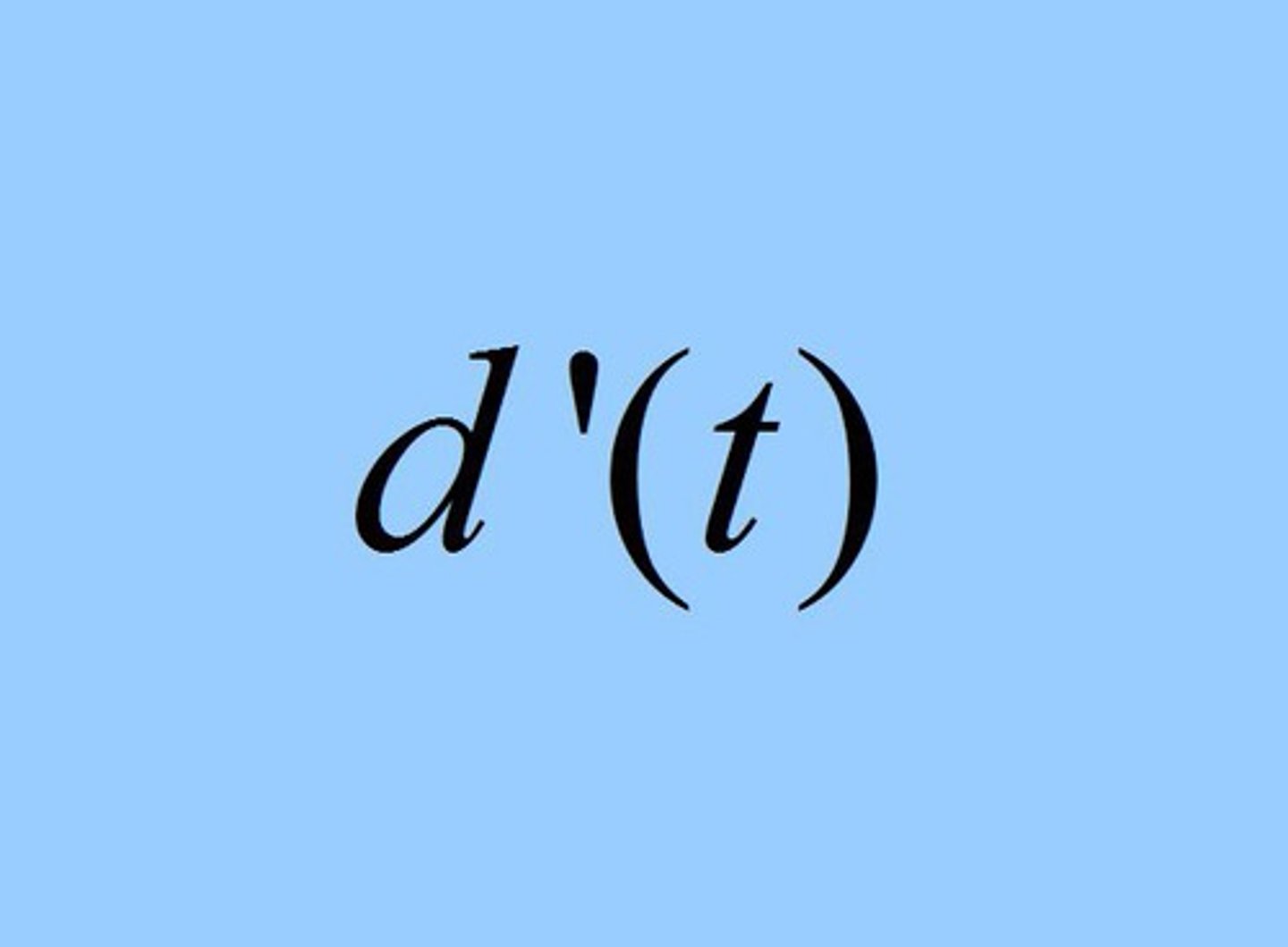
Speed of a point moving along a line

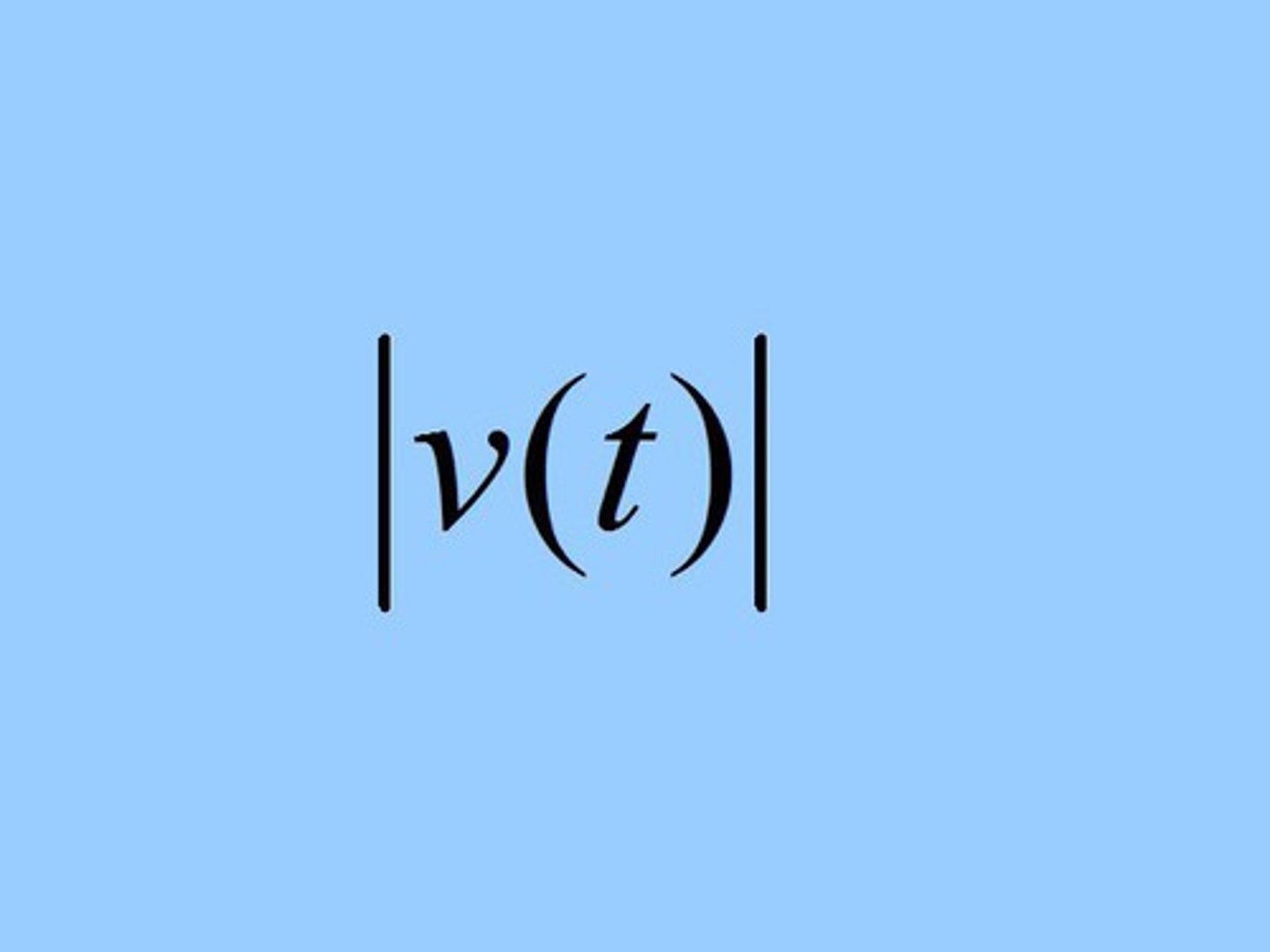
Average velocity

of s over [a, b]

Average acceleration

given v over [a, b]

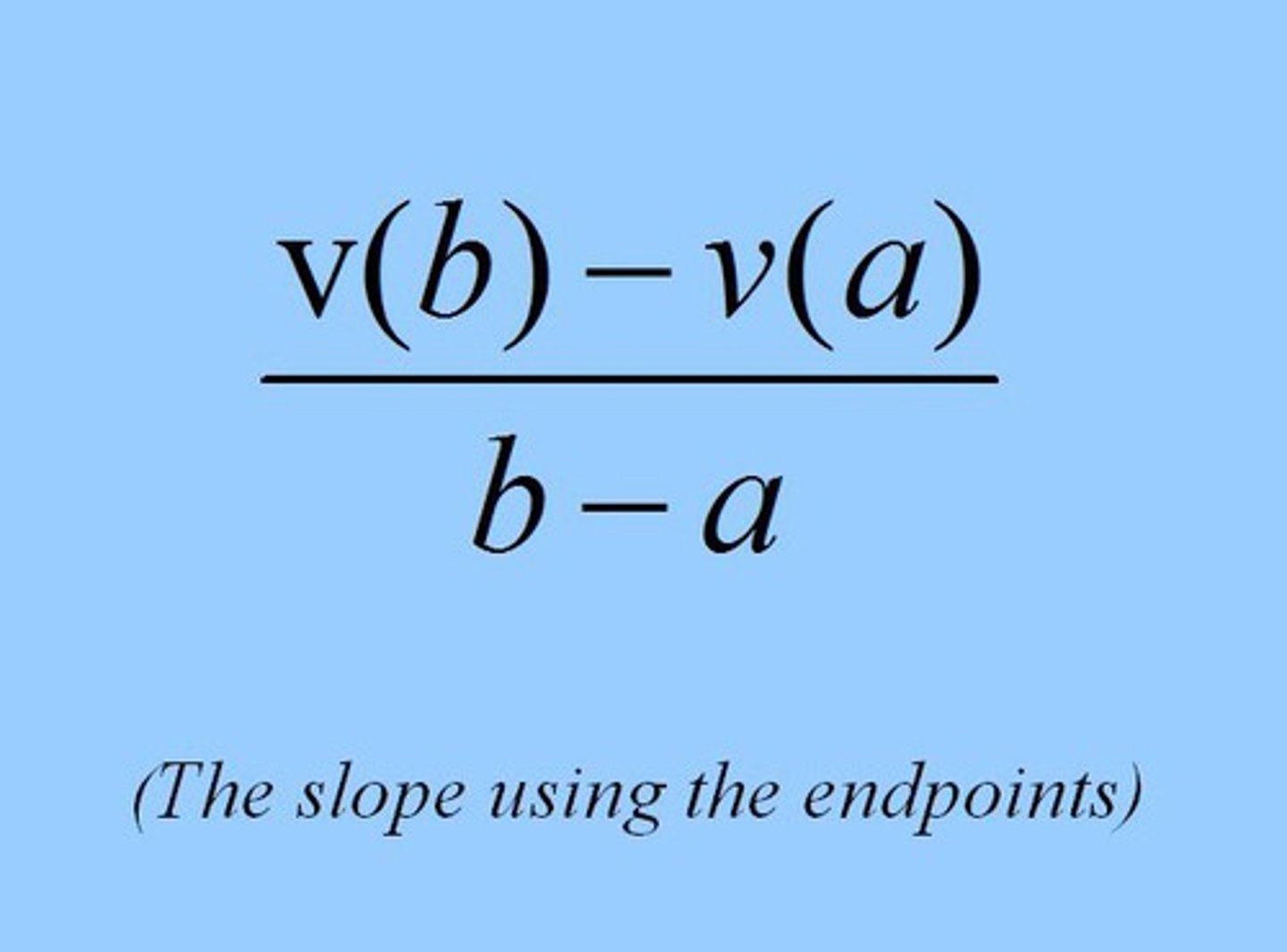
An object in motion is at rest when...

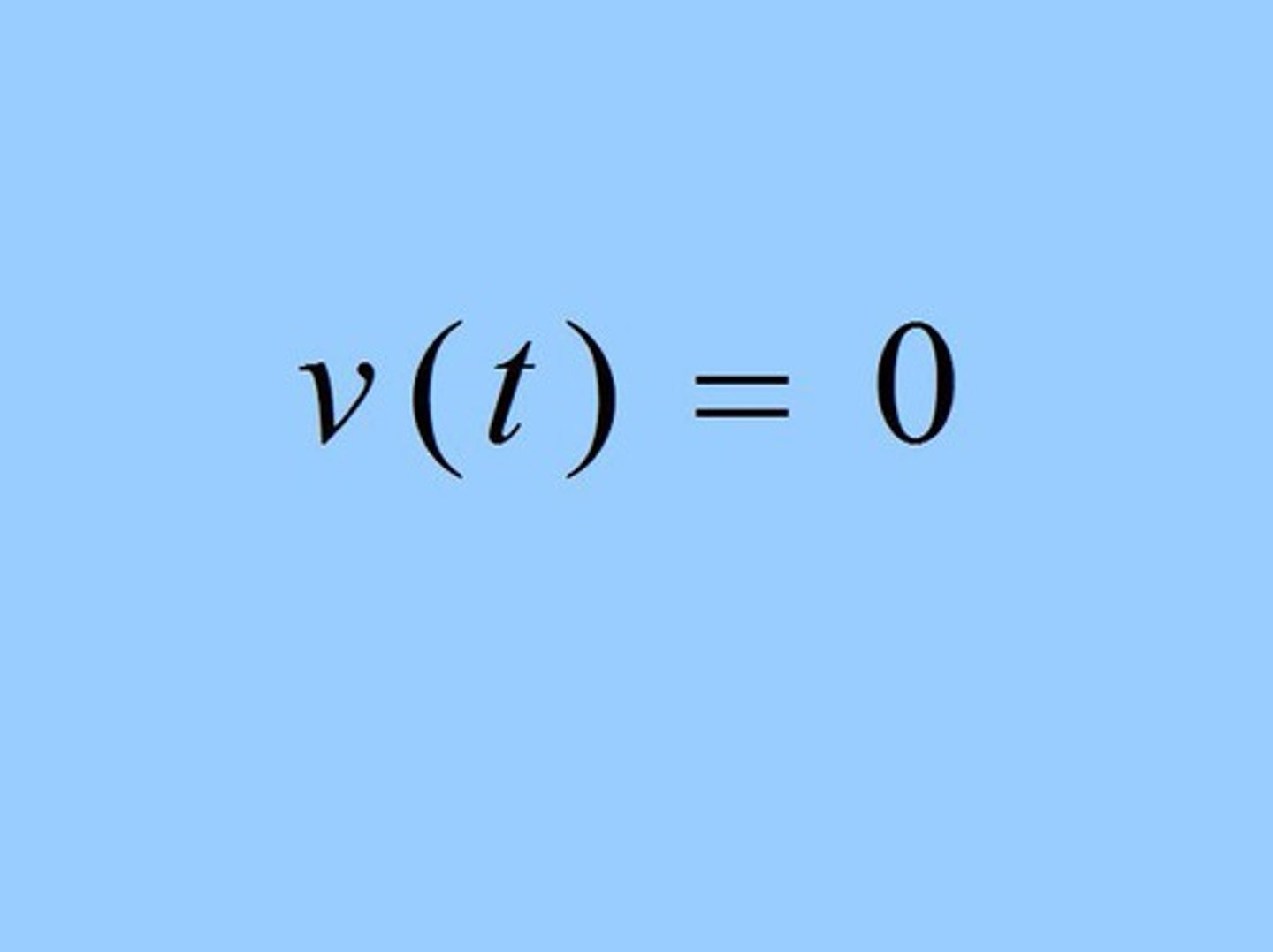
An object in motion reverses direction when...

Acceleration of a point moving along a line with position at time t given by d(t)

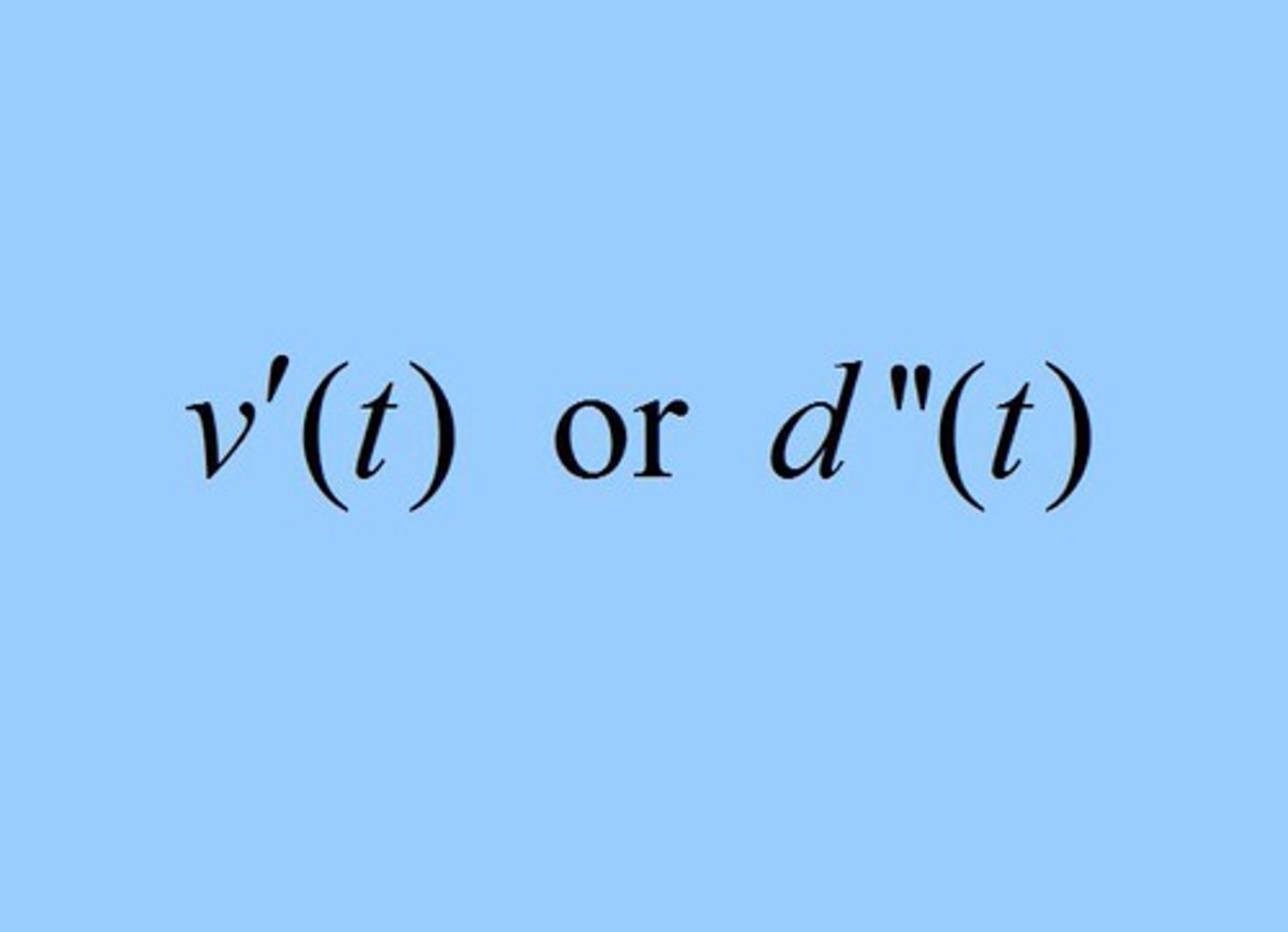
How to tell if a point moving along the x-axis with velocity v(t) is speeding up or slowing down at some time t?

Position at time t = b of a particle moving along a line given velocity v(t) and position s(t) at time t = a

Displacement of a particle moving along a line with velocity v(t) for a ≤ t ≤ b.

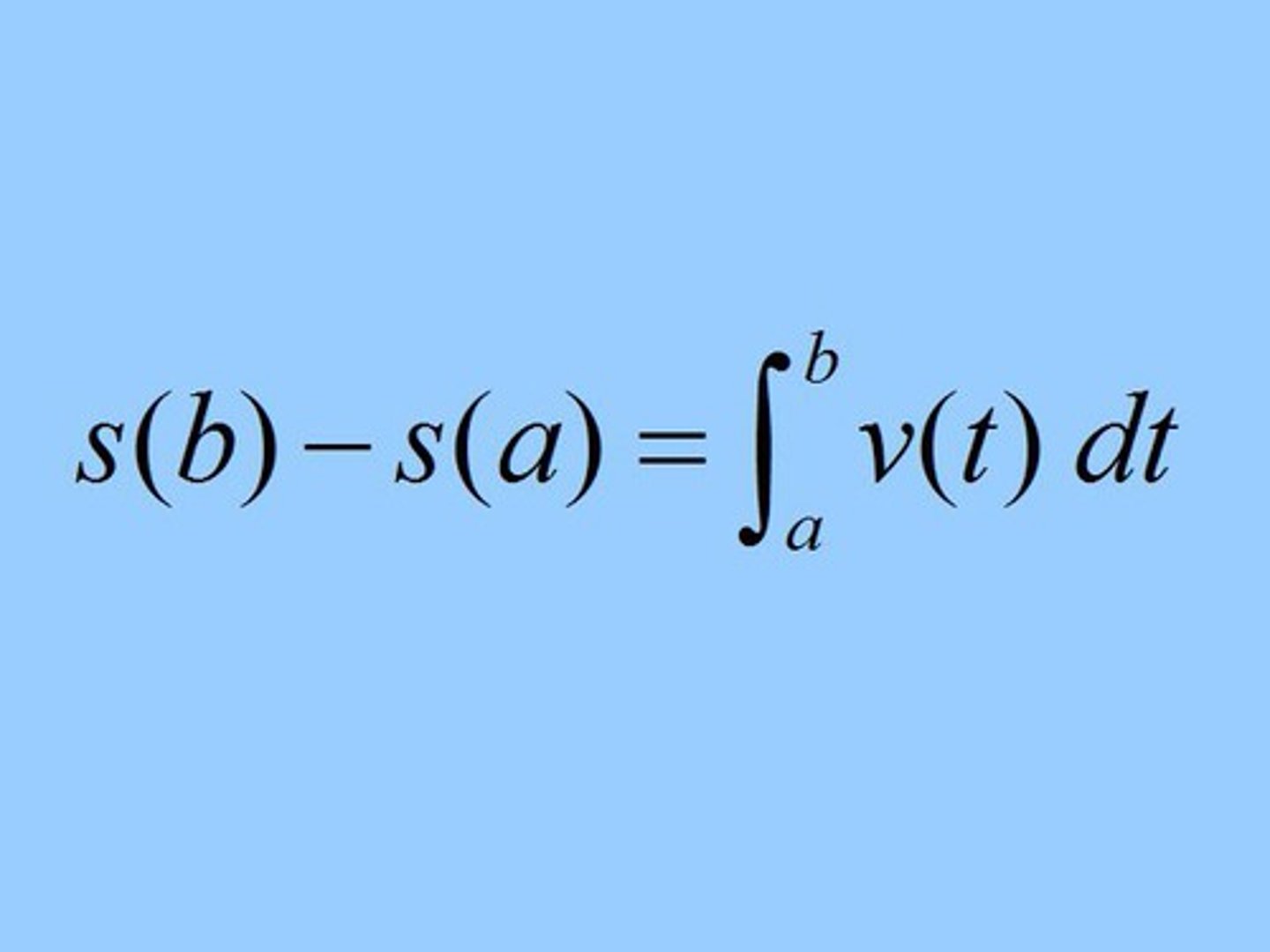
Total distance traveled by a particle moving along a line with velocity v(t) for a ≤ t ≤ b

...

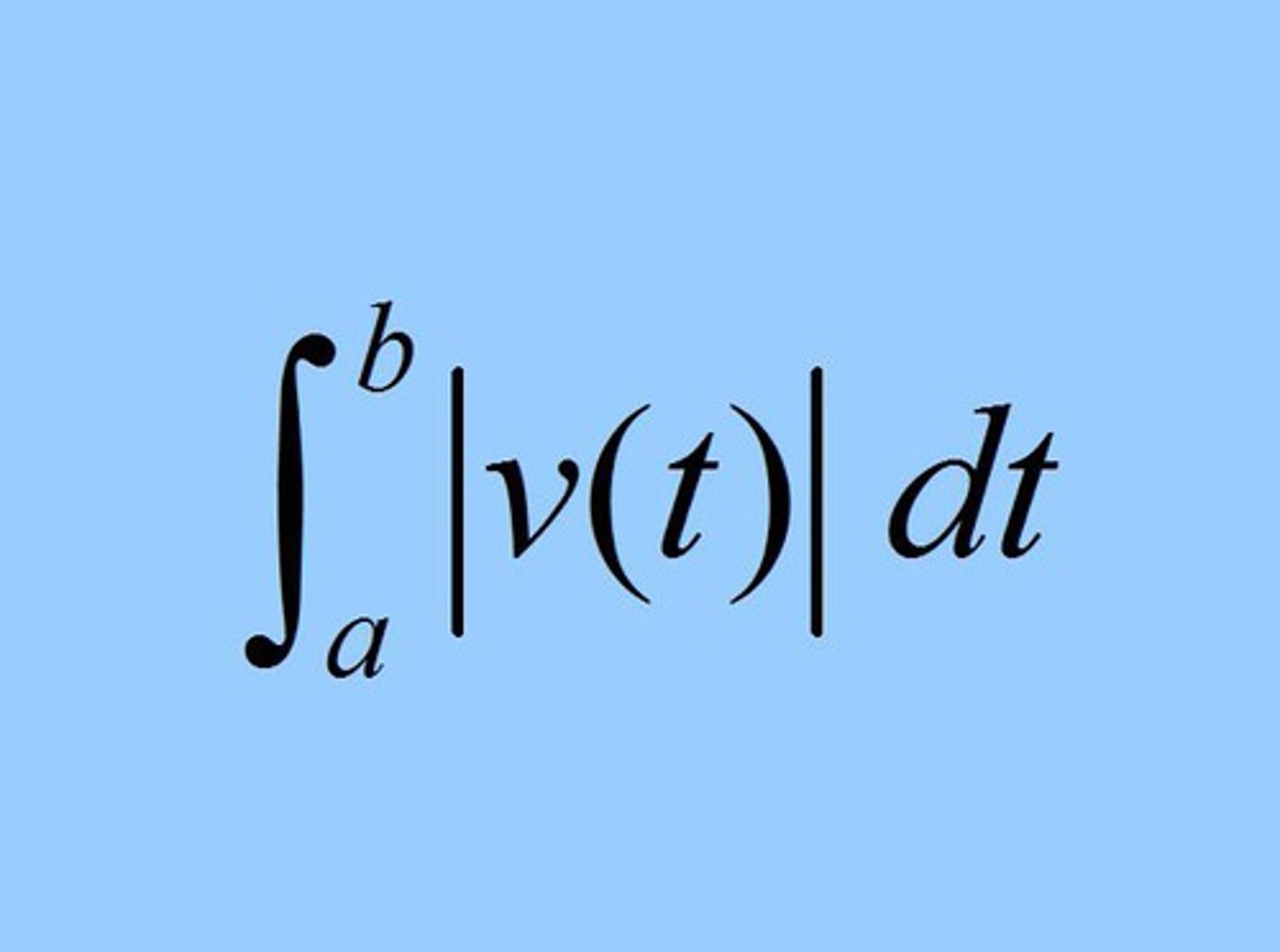
The total change in ƒ(x) over [a, b] in terms of the rate of change, ƒ'(x)

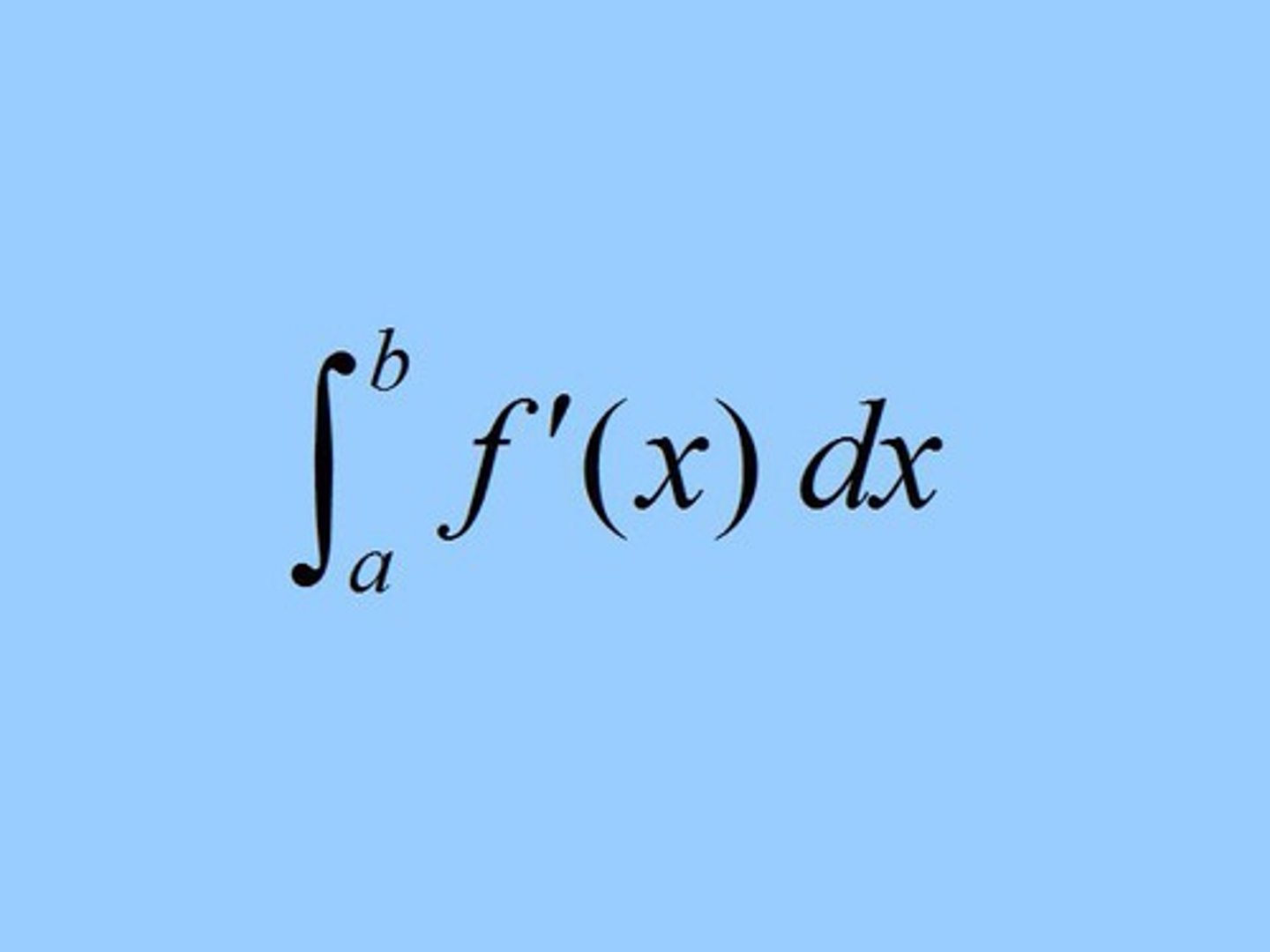
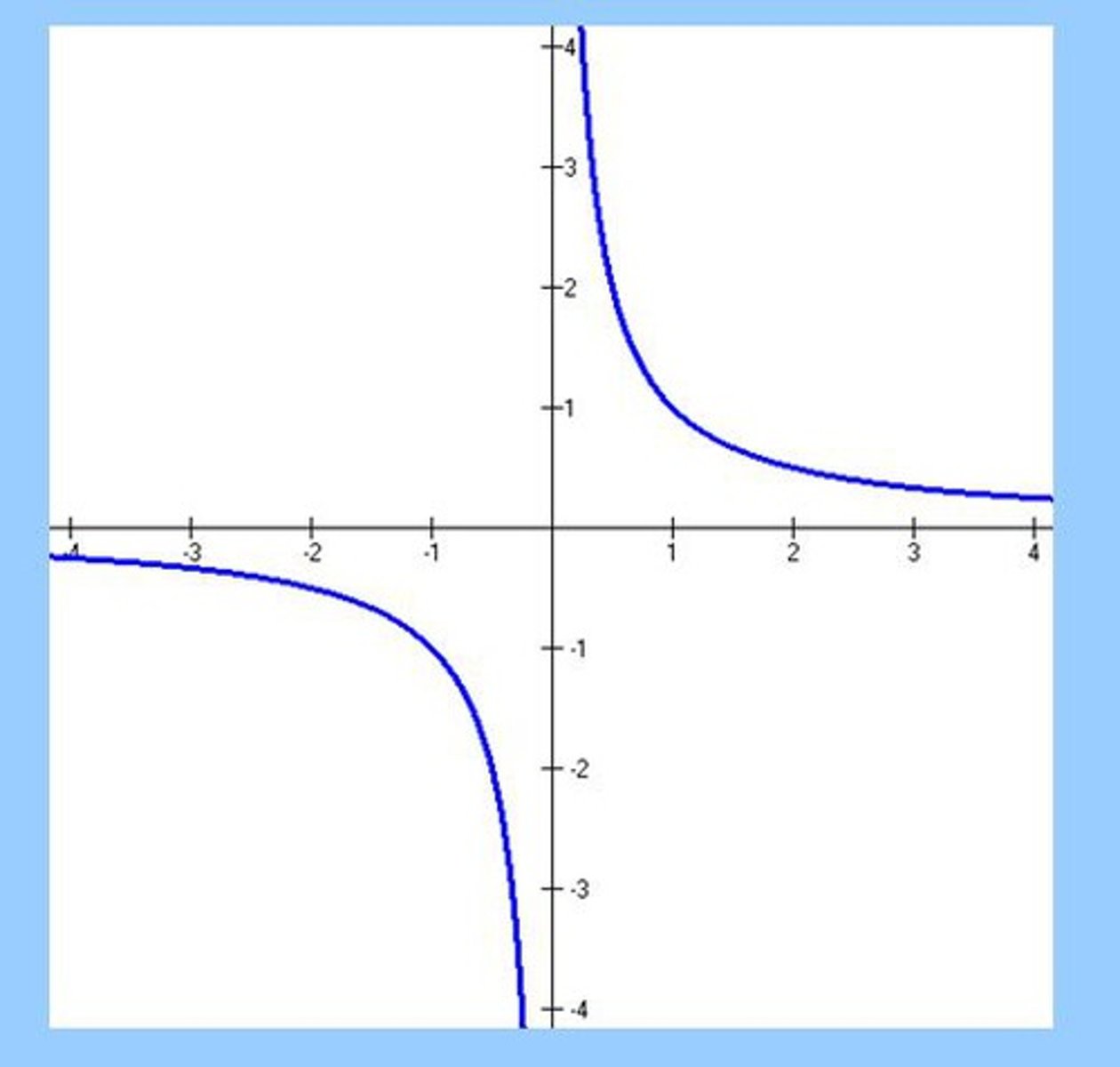
Graph of y = 1/x

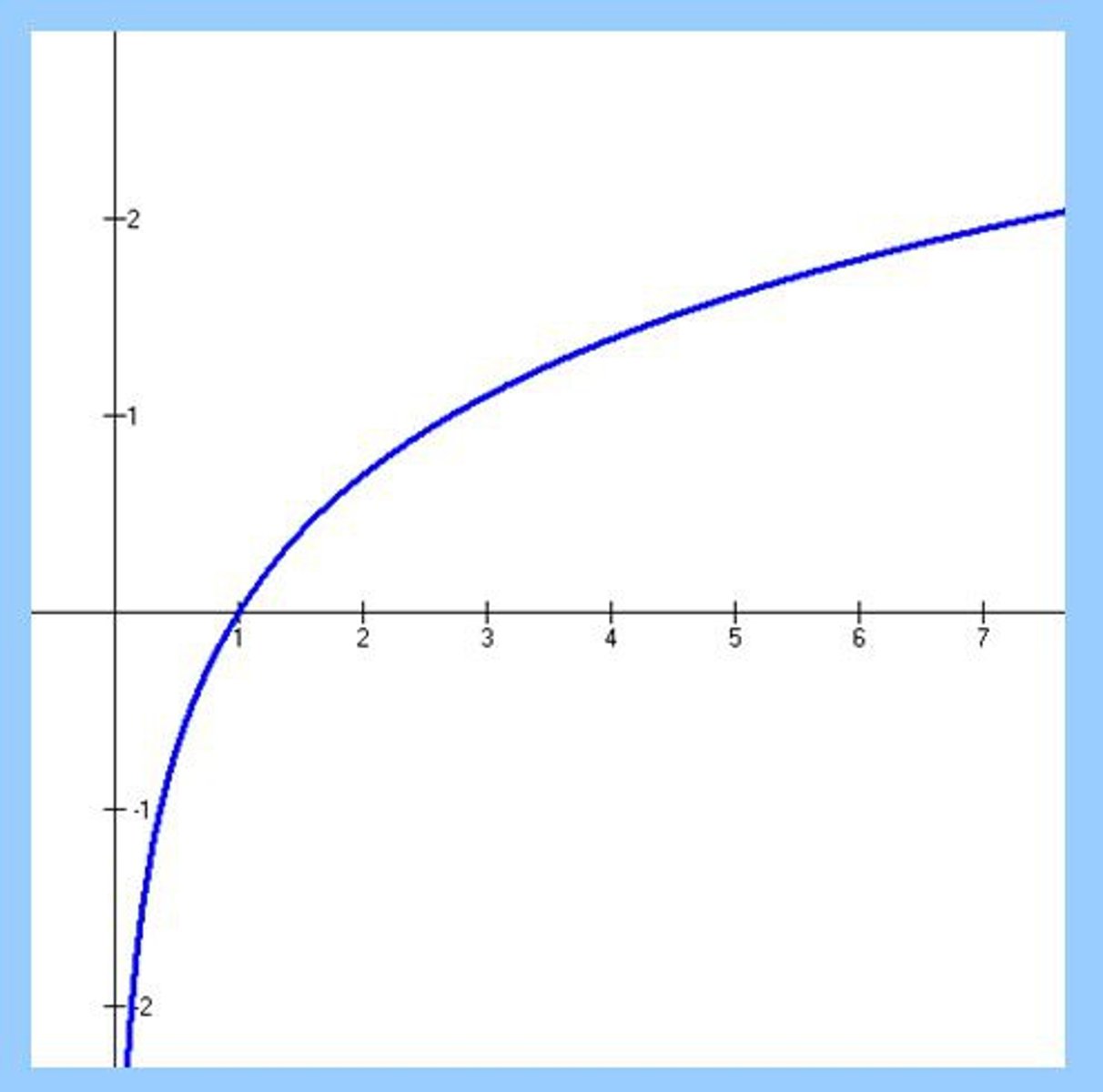
Graph of y = e ^ (kx)

Graph of y = ln x

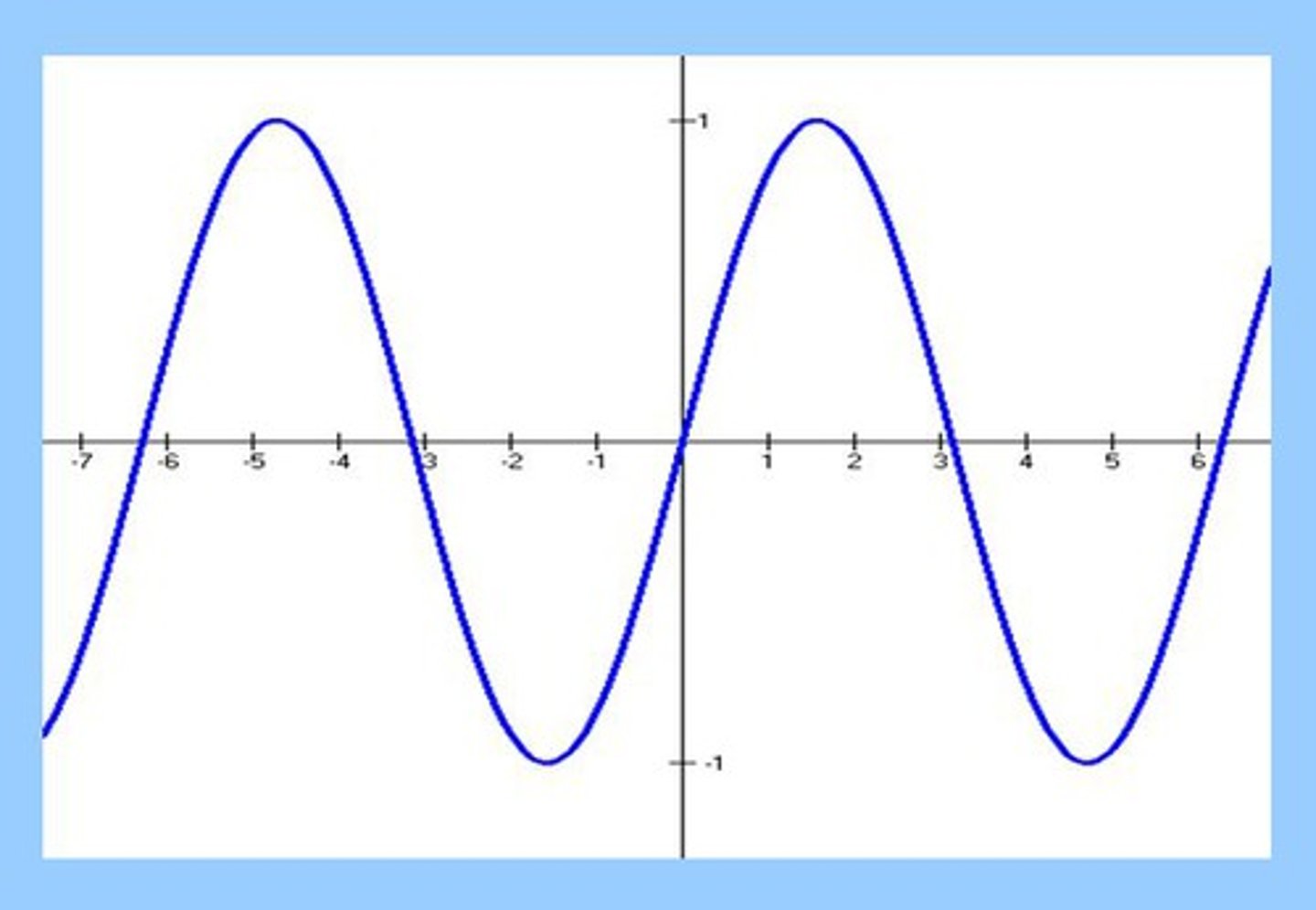
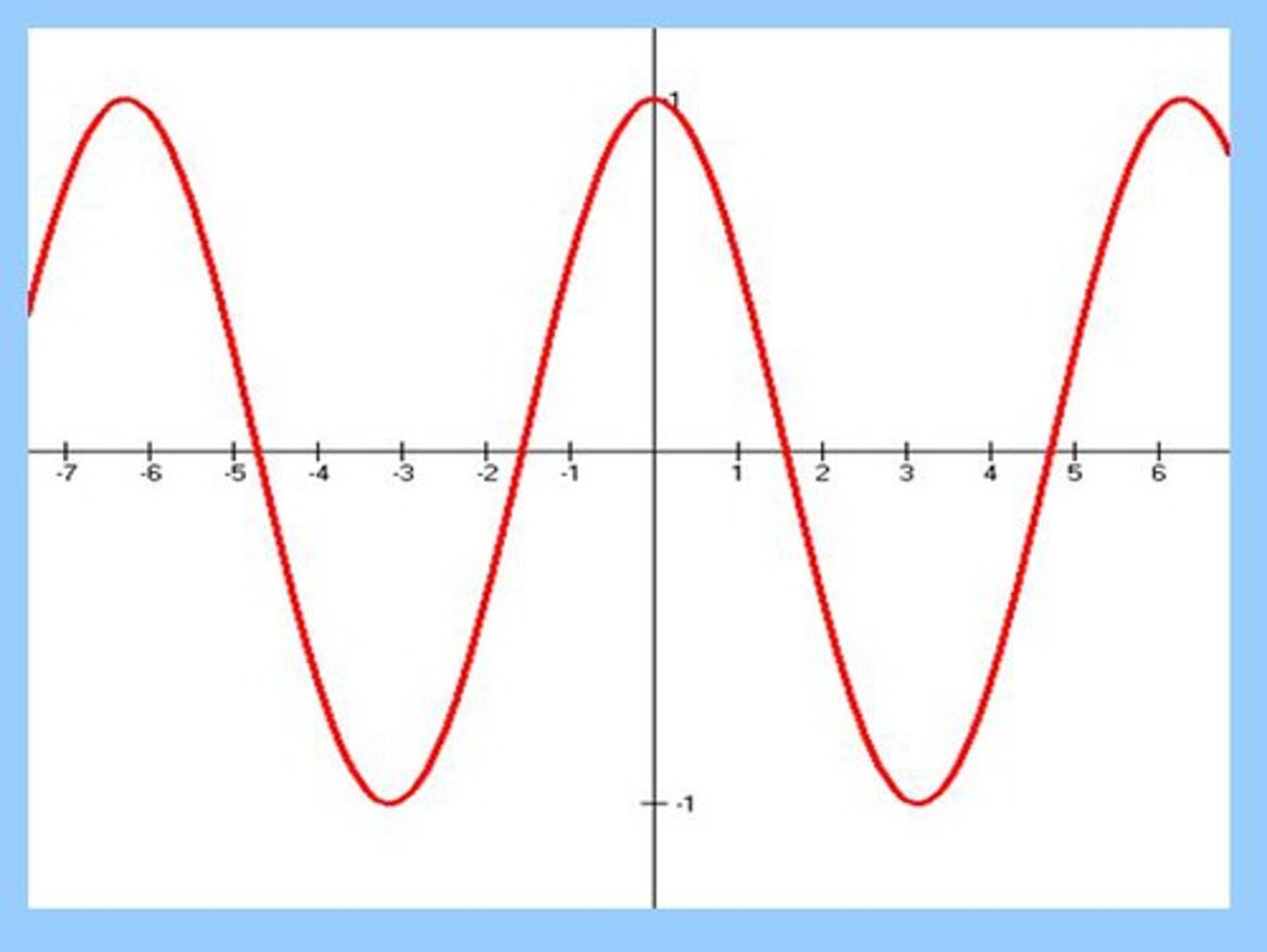
Graph of y = sin x

Graph of y = cos x

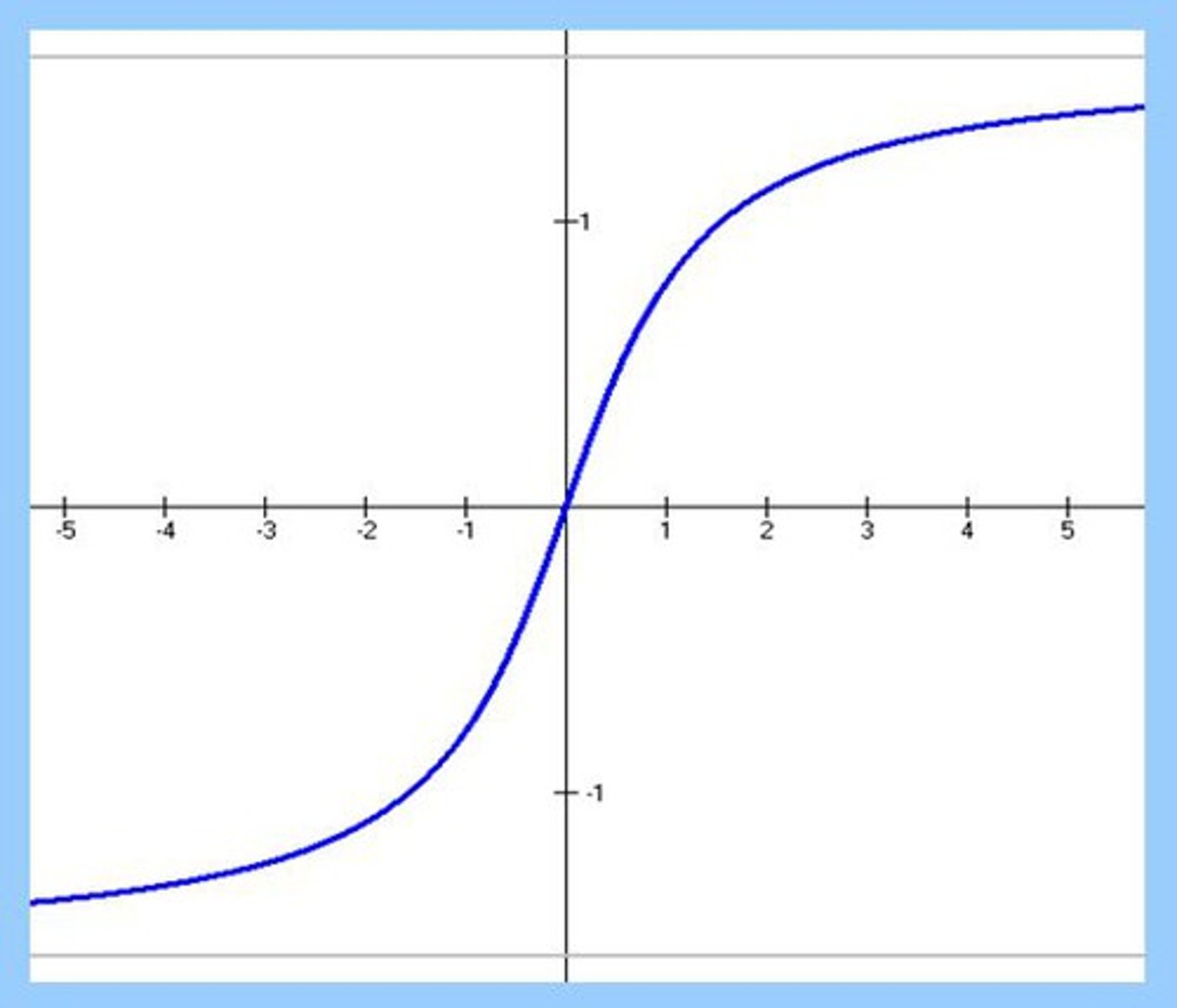
Graph of y = tan⁻¹ x

L'Hopital's Rule

To find the limits of

indeterminate forms:

∞ × 0

To find the limits of

indeterminate forms:

0 ^ 0, 1 ^ ∞, ∞ ^ 0

If ƒ(x) is increasing, then a left Riemann sum ...

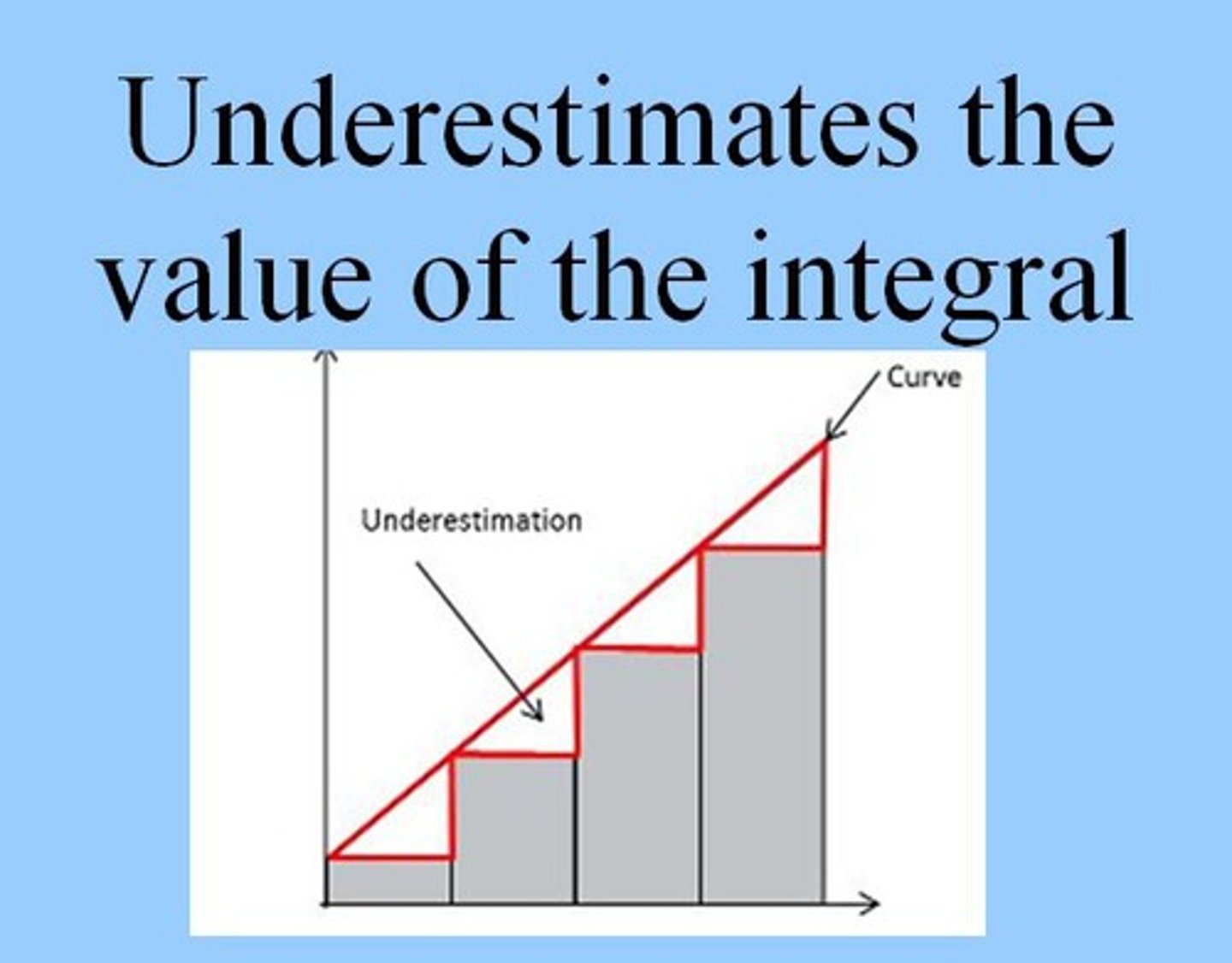
If ƒ(x) is decreasing, then a left Riemann sum ...

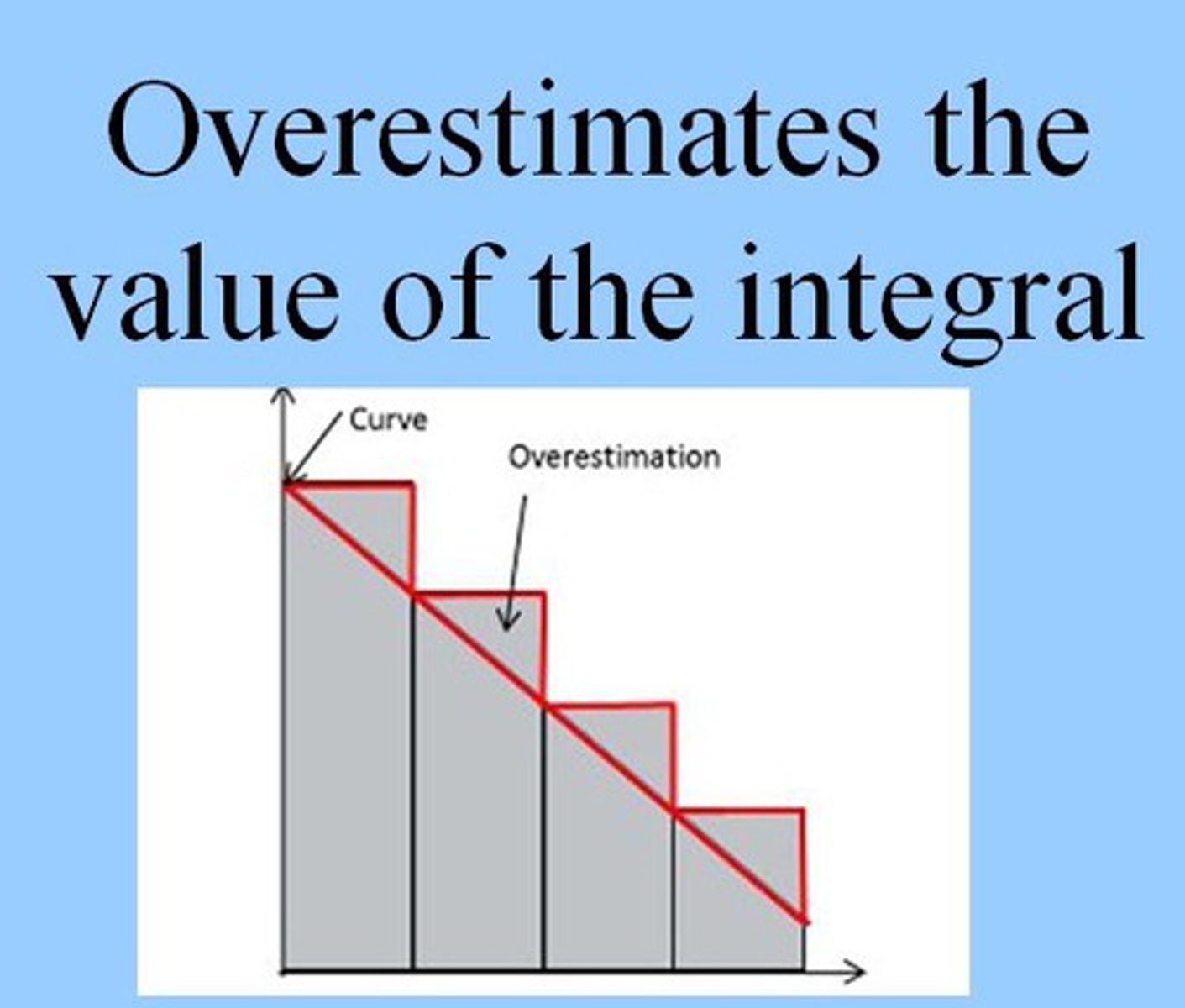
If ƒ(x) is increasing, then a right Riemann sum ...

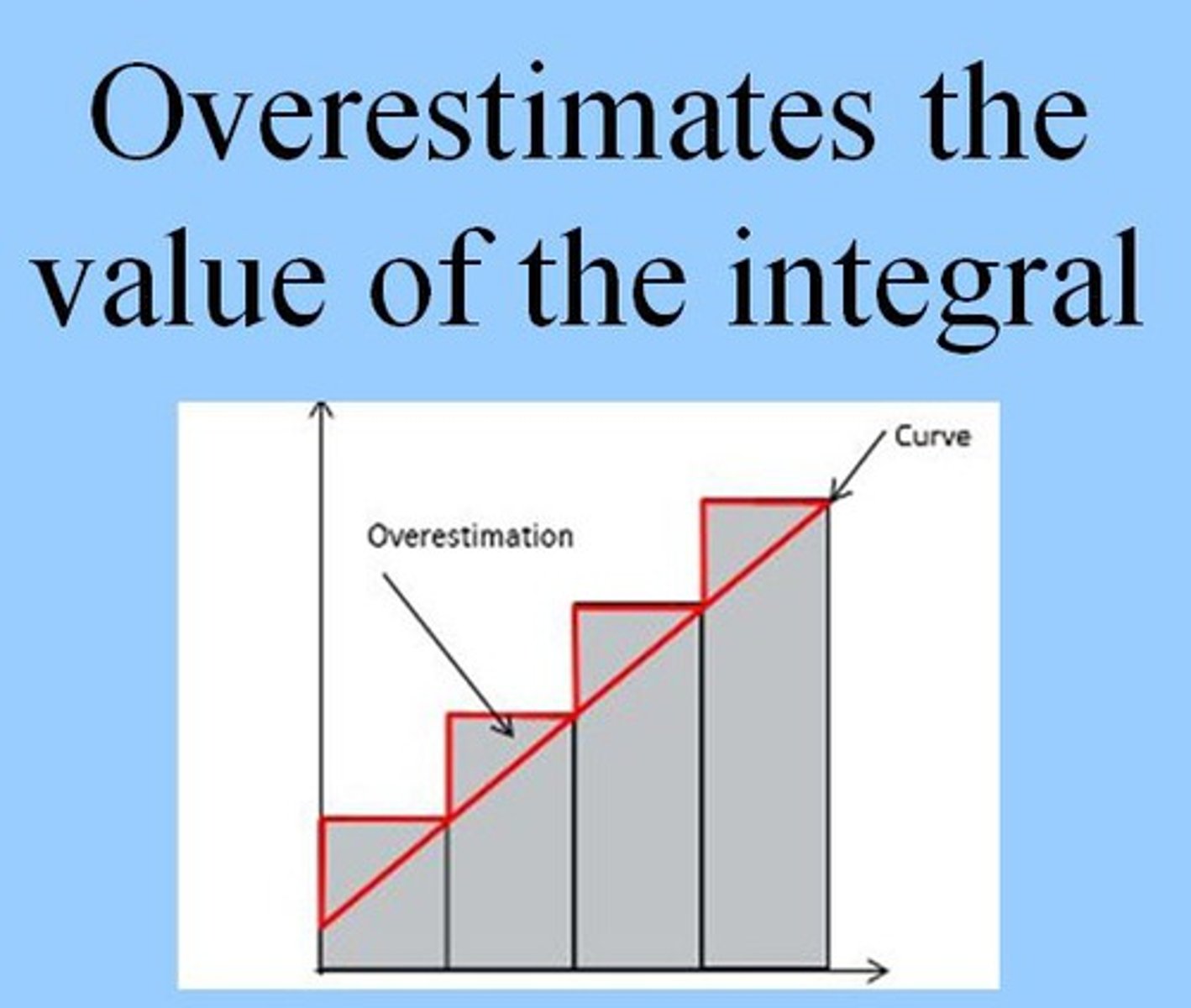
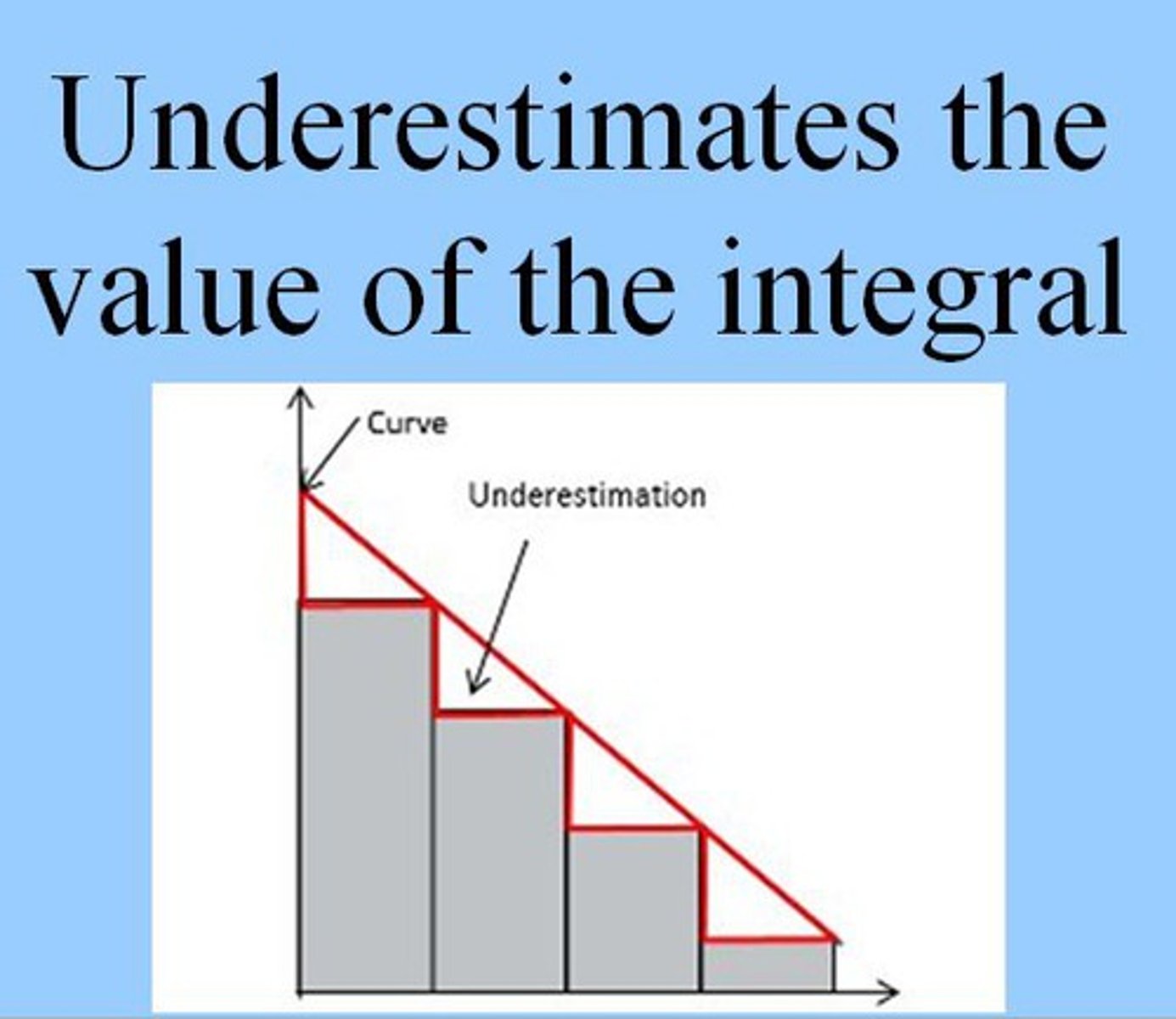
If ƒ(x) is decreasing, then a right Riemann sum ...

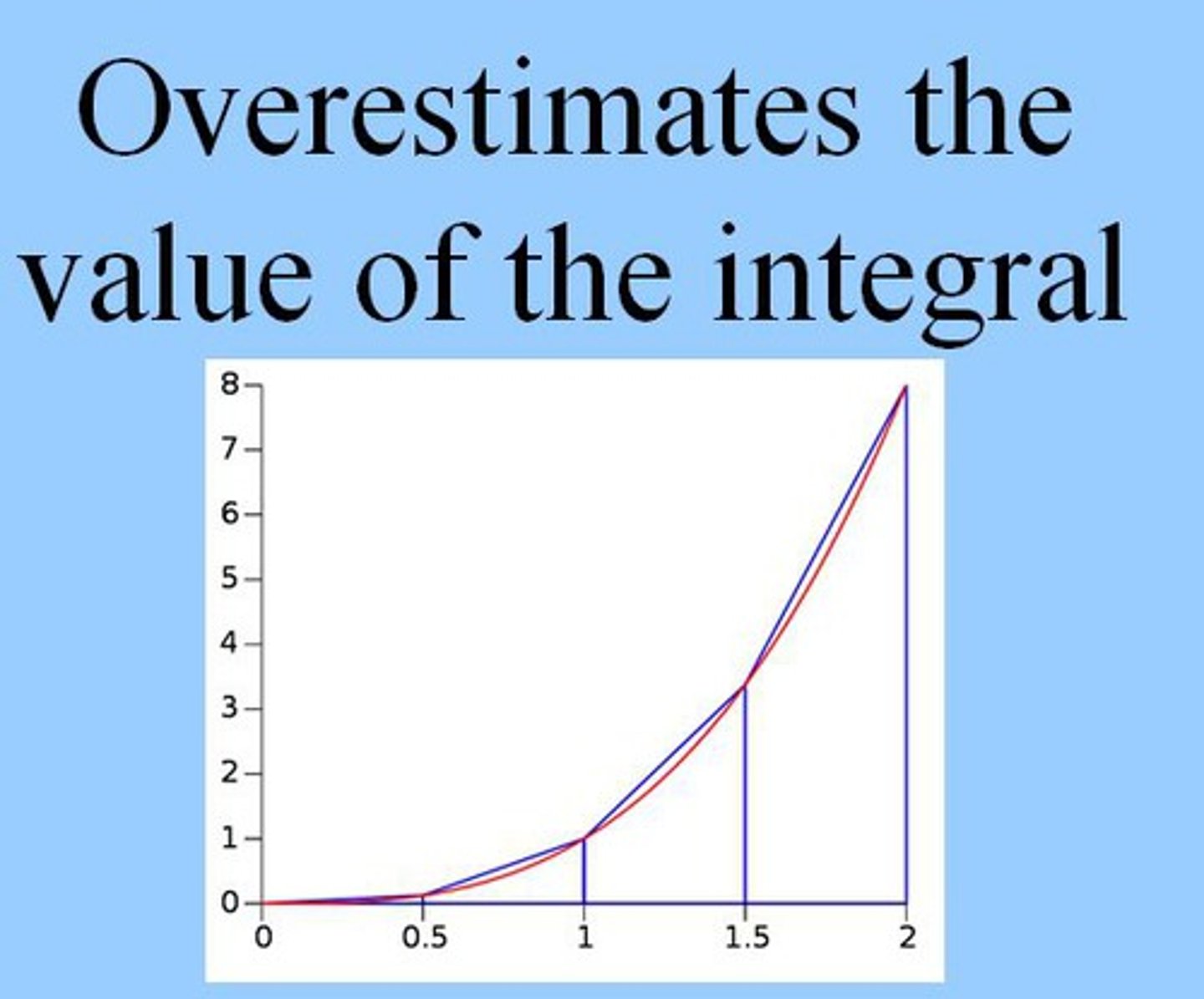
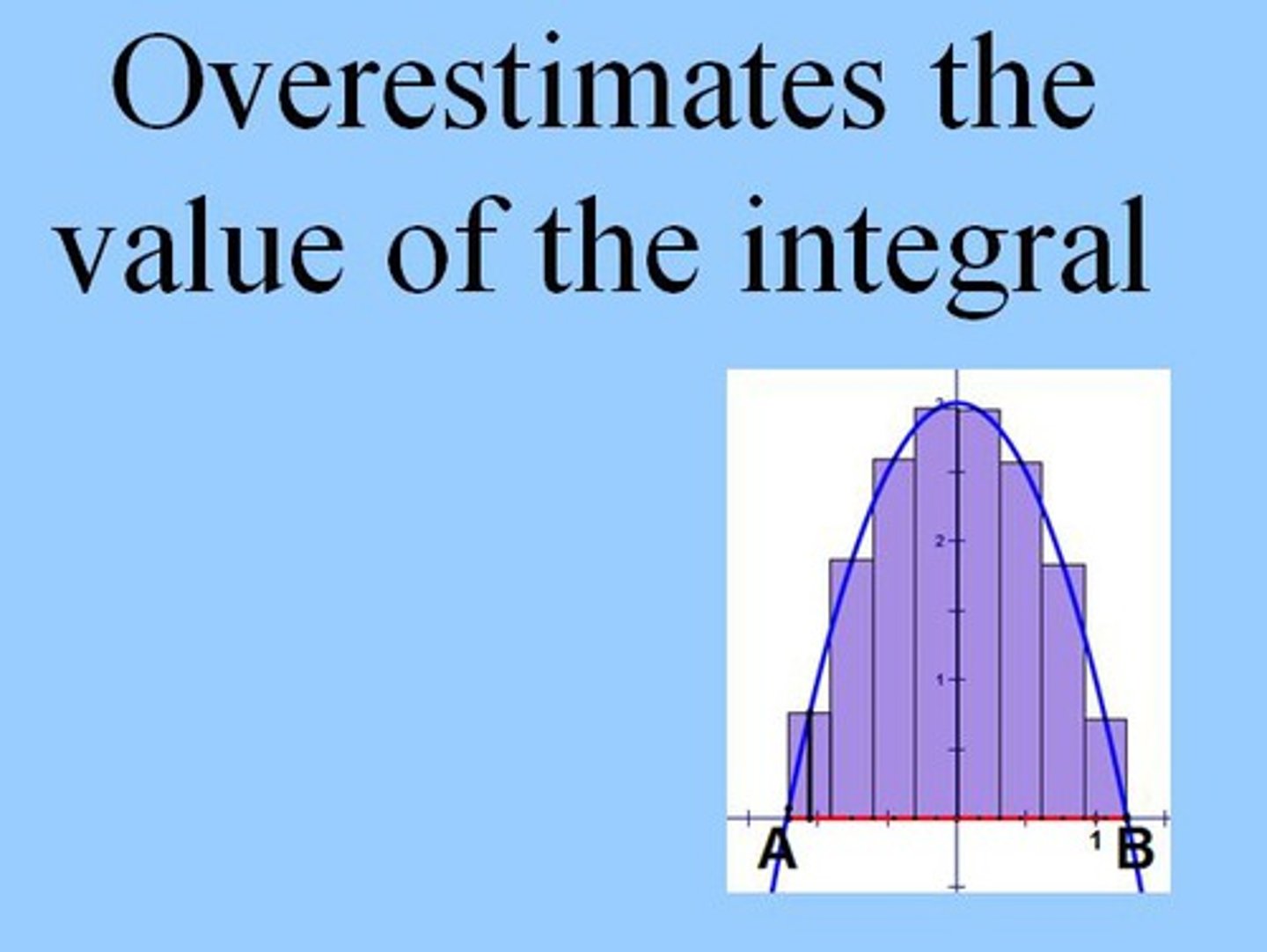
If ƒ(x) is concave up, then the trapezoidal approximation of the integral...

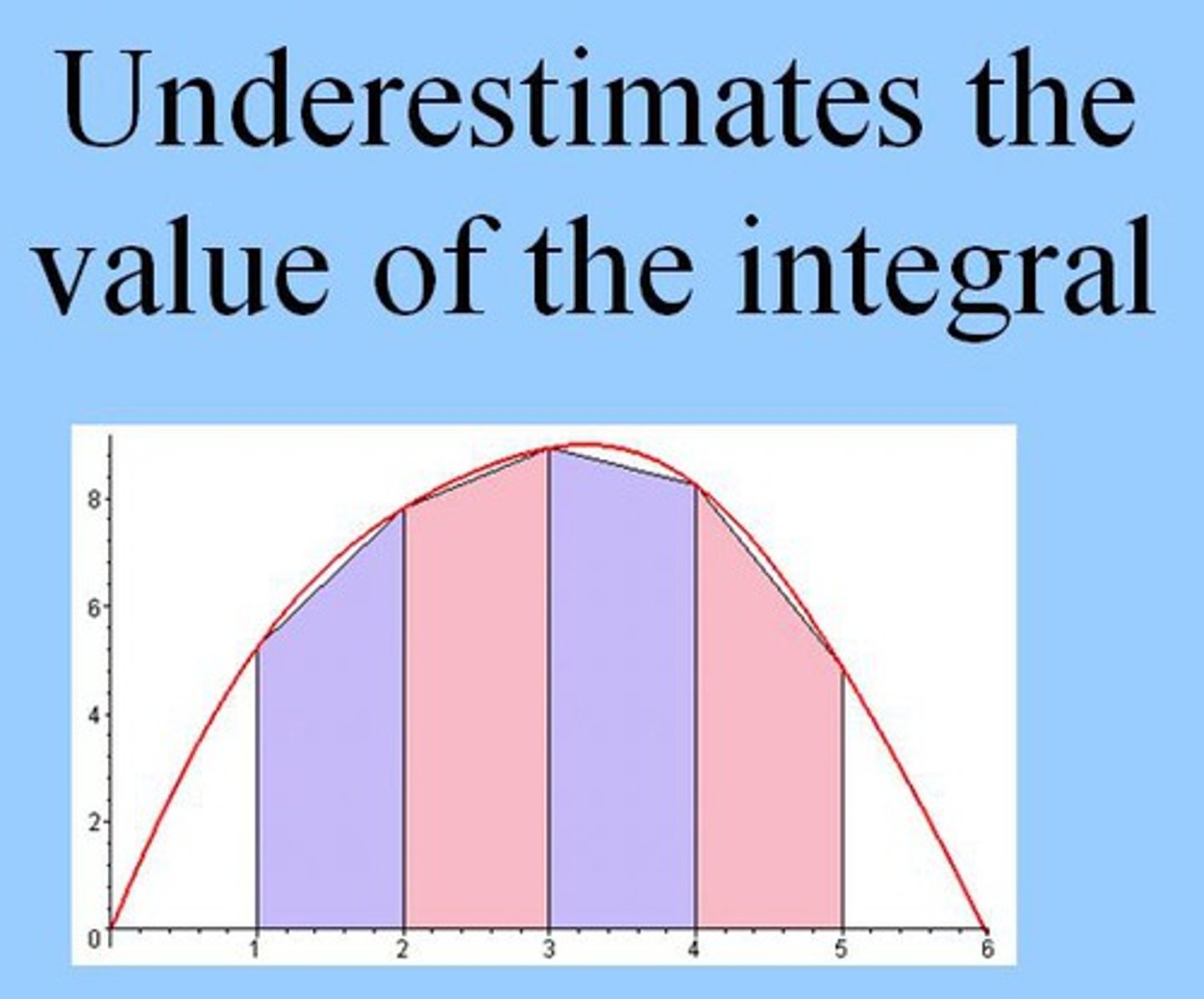
If ƒ(x) is concave down, then the trapezoidal approximation of the integral...

If ƒ(x) is concave up, then a midpoint Riemann sum...

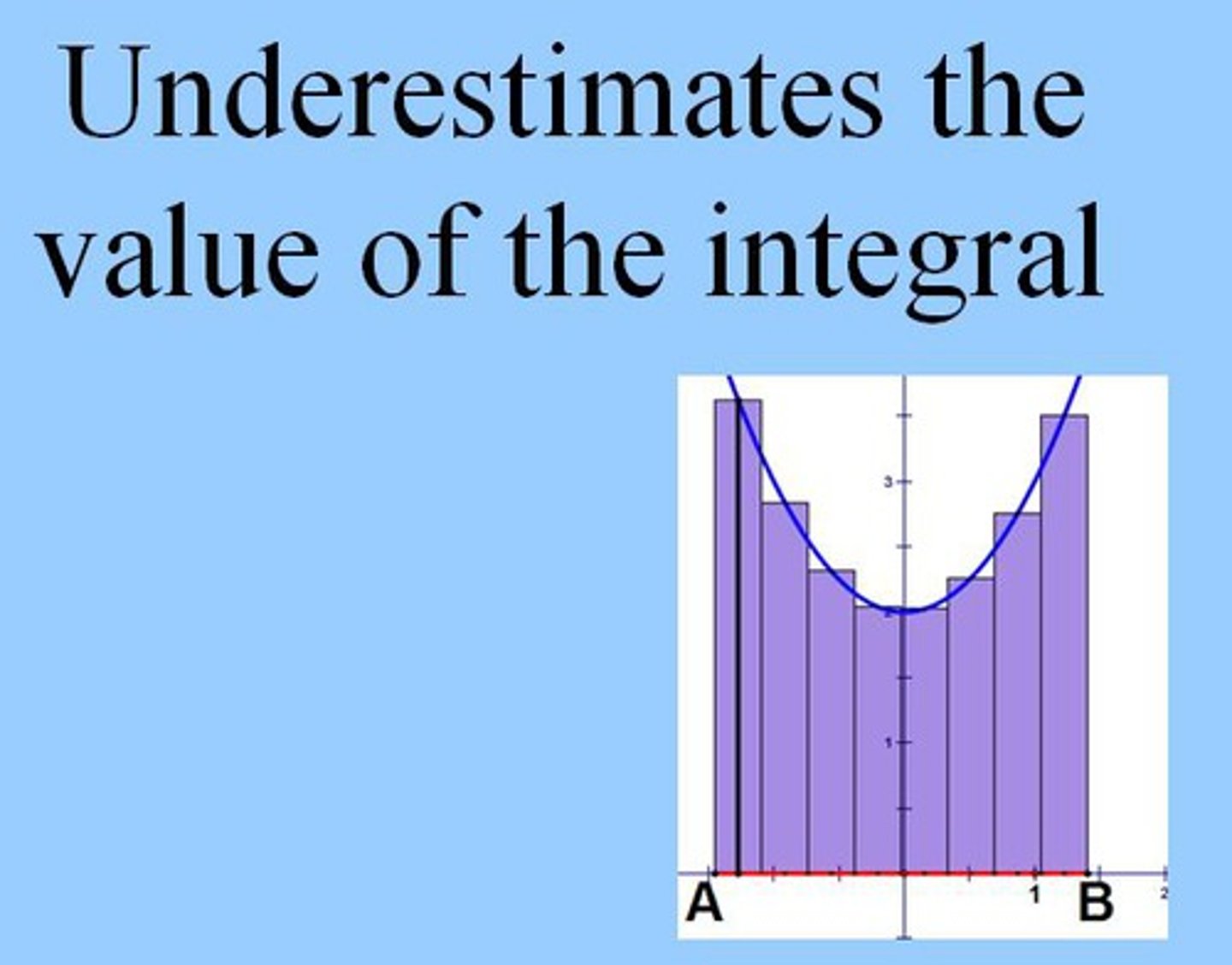
If ƒ(x) is concave down, then a midpoint Riemann sum...

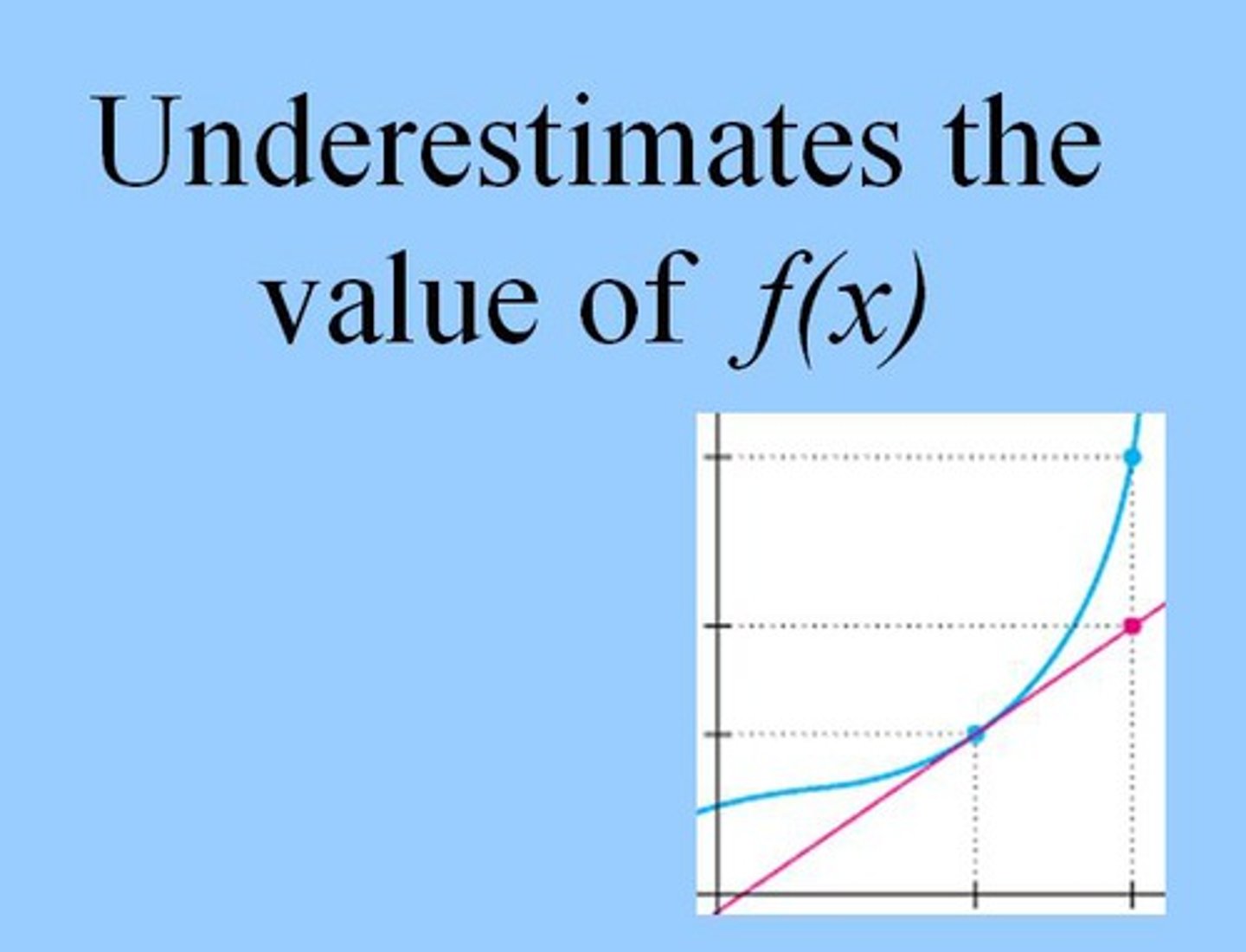
If ƒ(x) is concave down then the linear approximation...

If ƒ(x) is concave up then the linear approximation...

The Fundamental Theorem of Calculus (Part I)

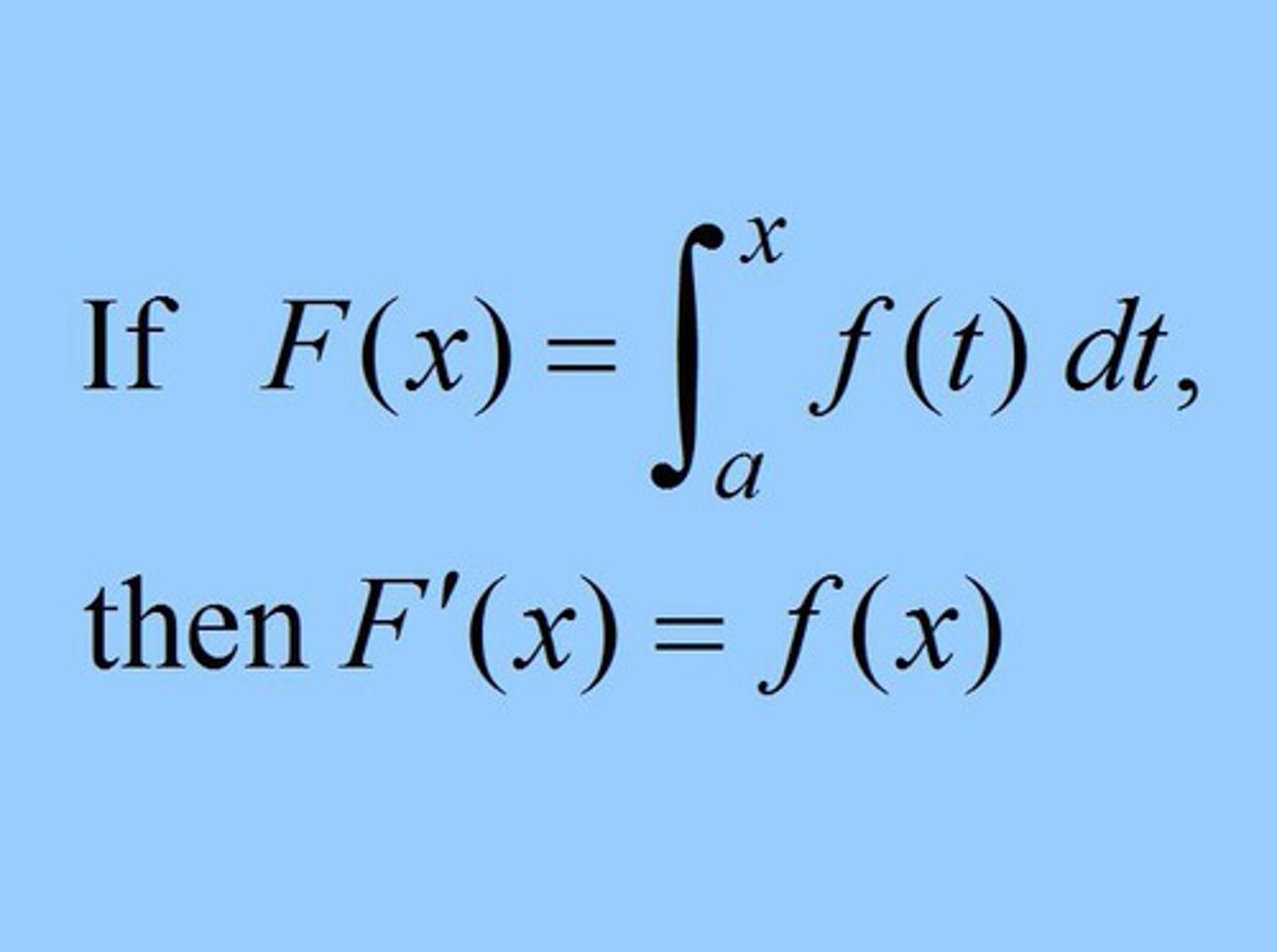
The Fundamental Theorem of Calculus (Part II)

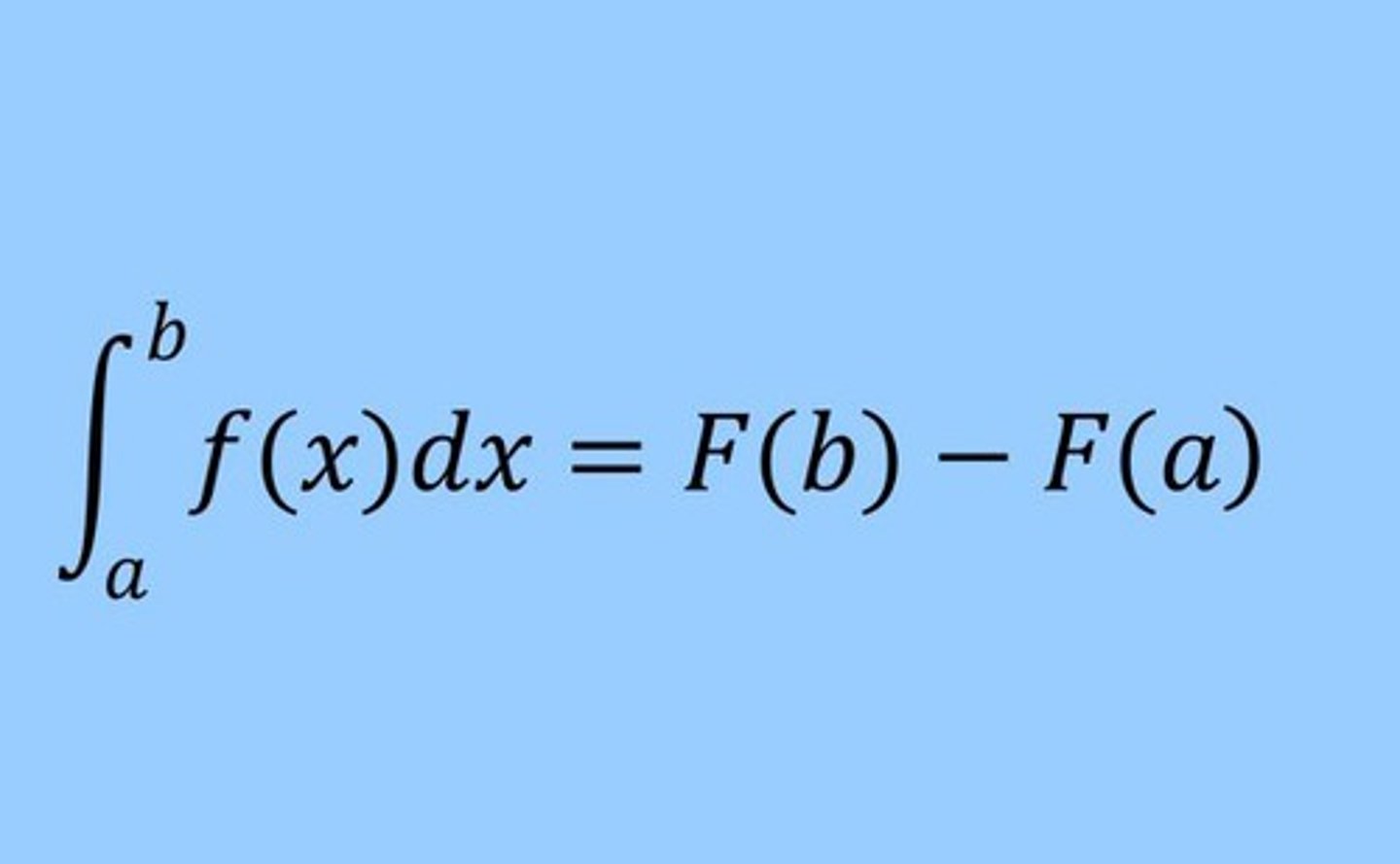
∫ x ^ n dx =

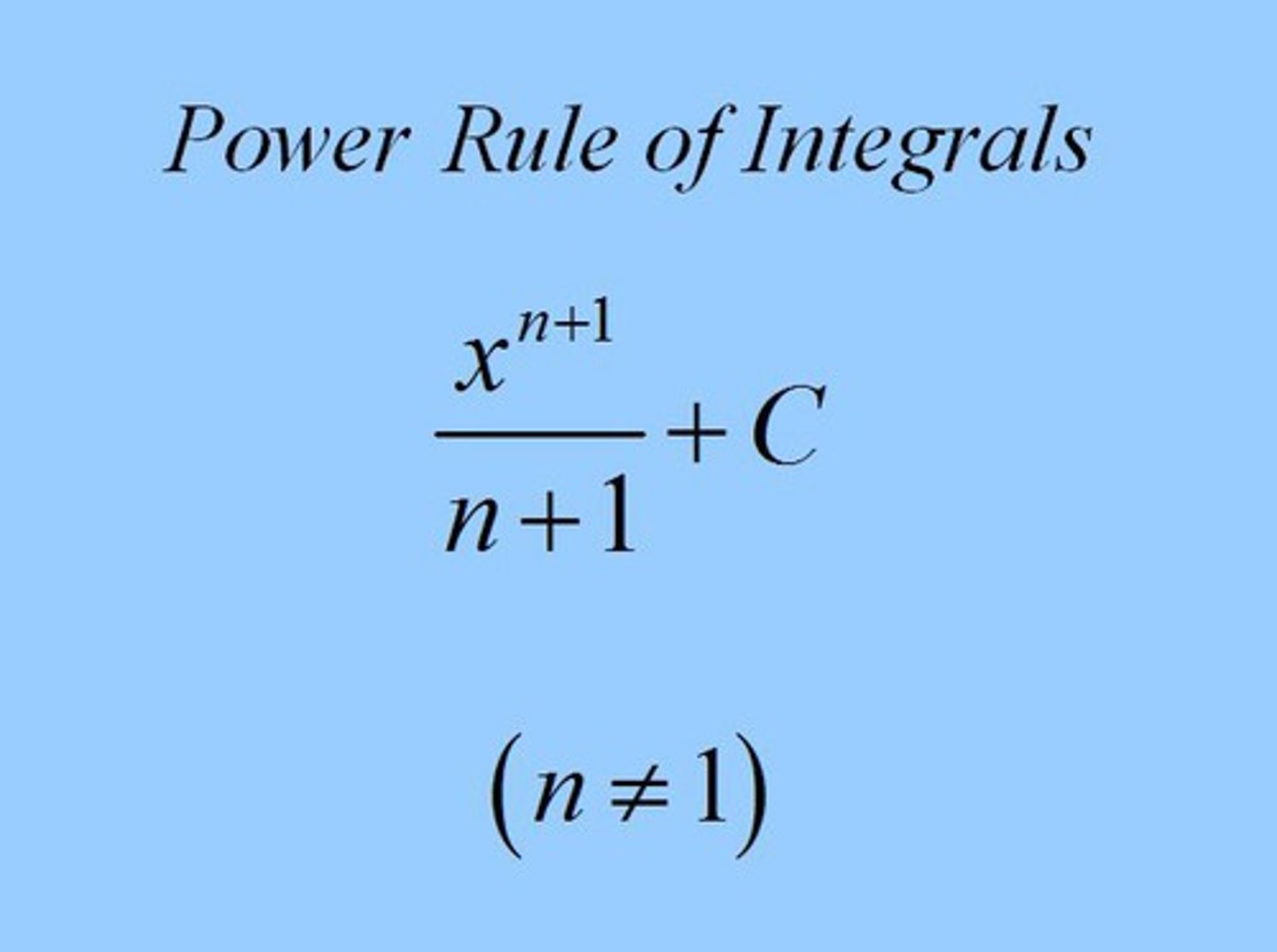
∫ e ^ x dx =

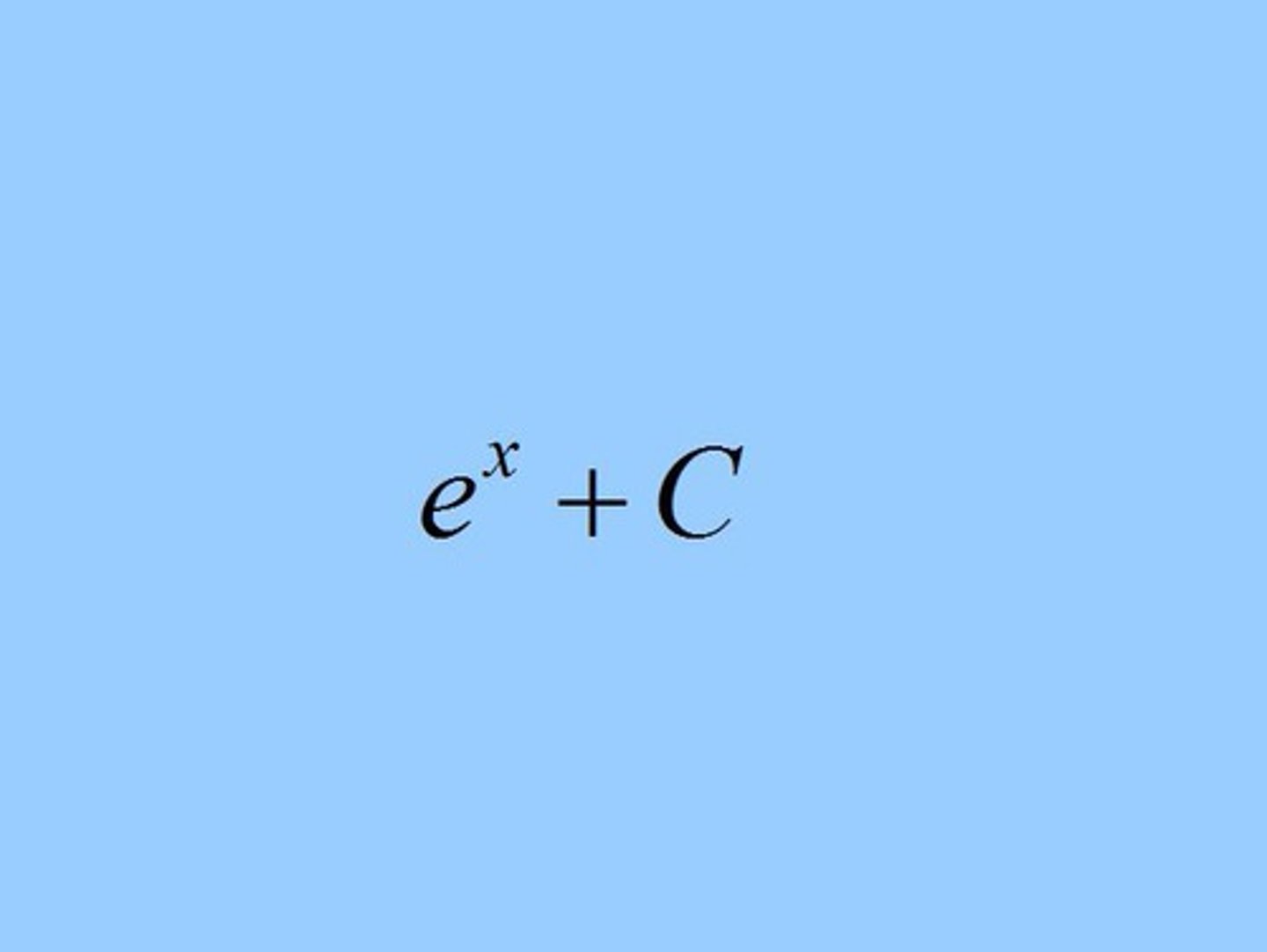
∫ 1/x dx =

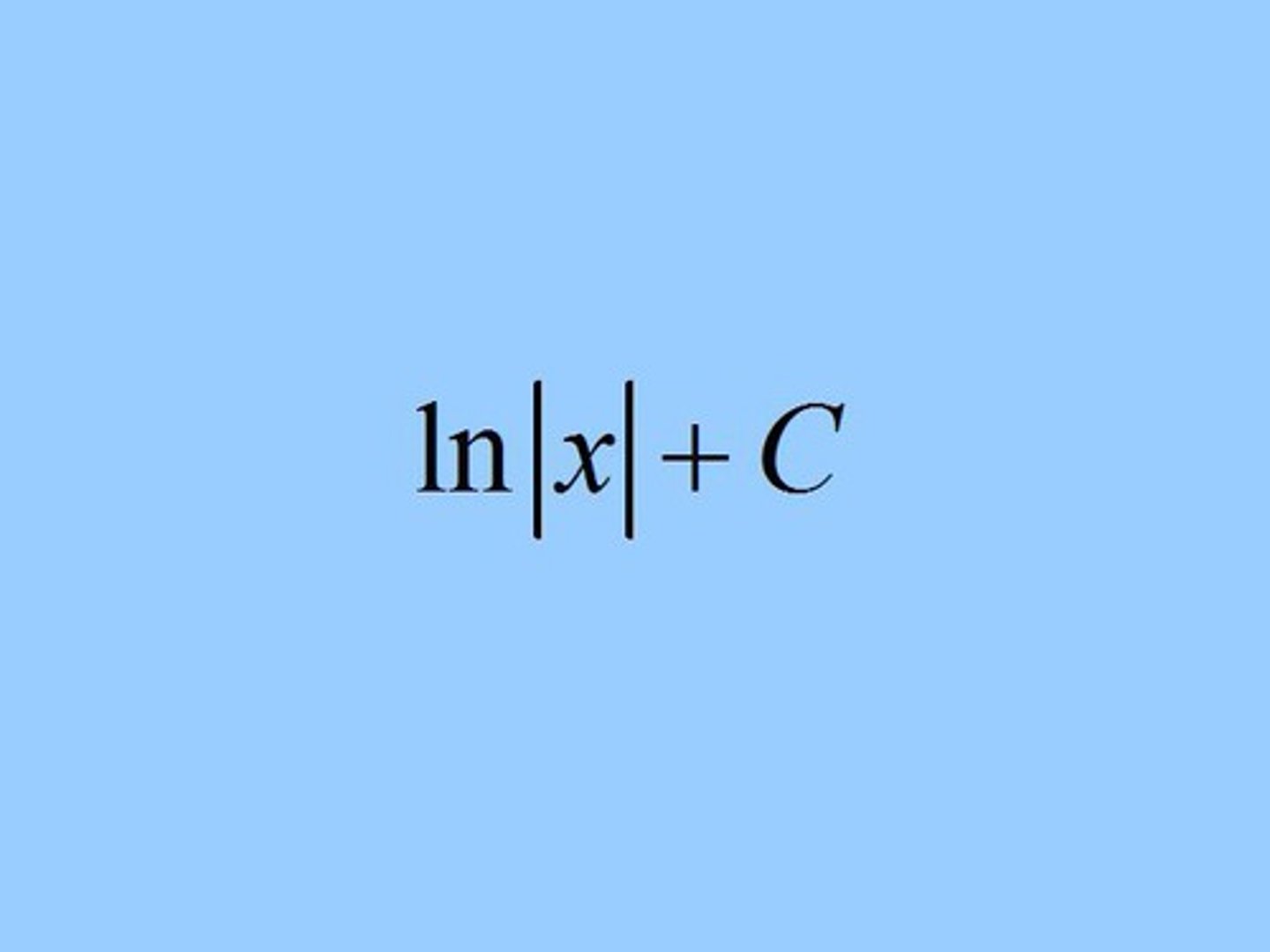
∫ sin x dx =

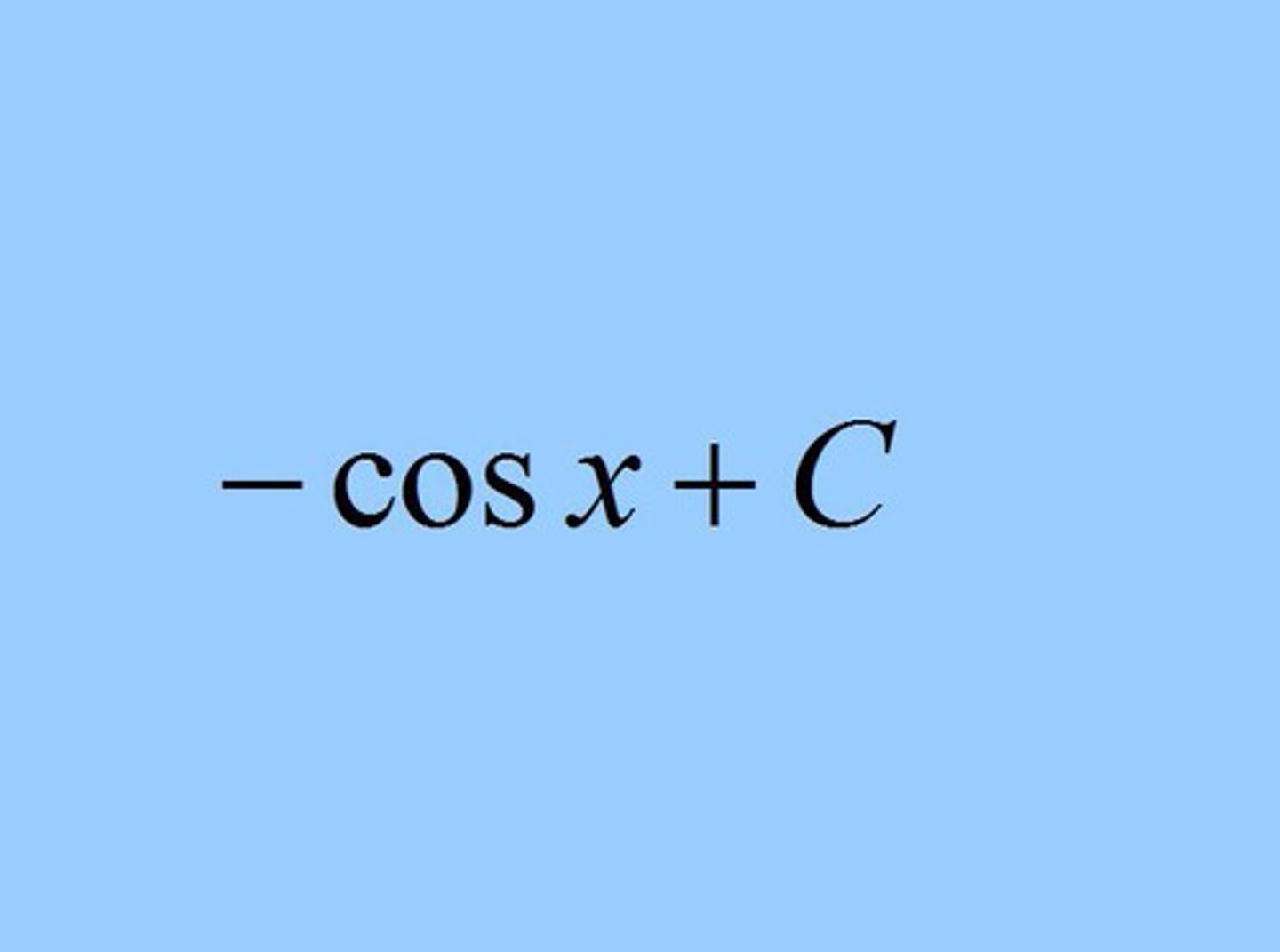
∫ cos x dx =

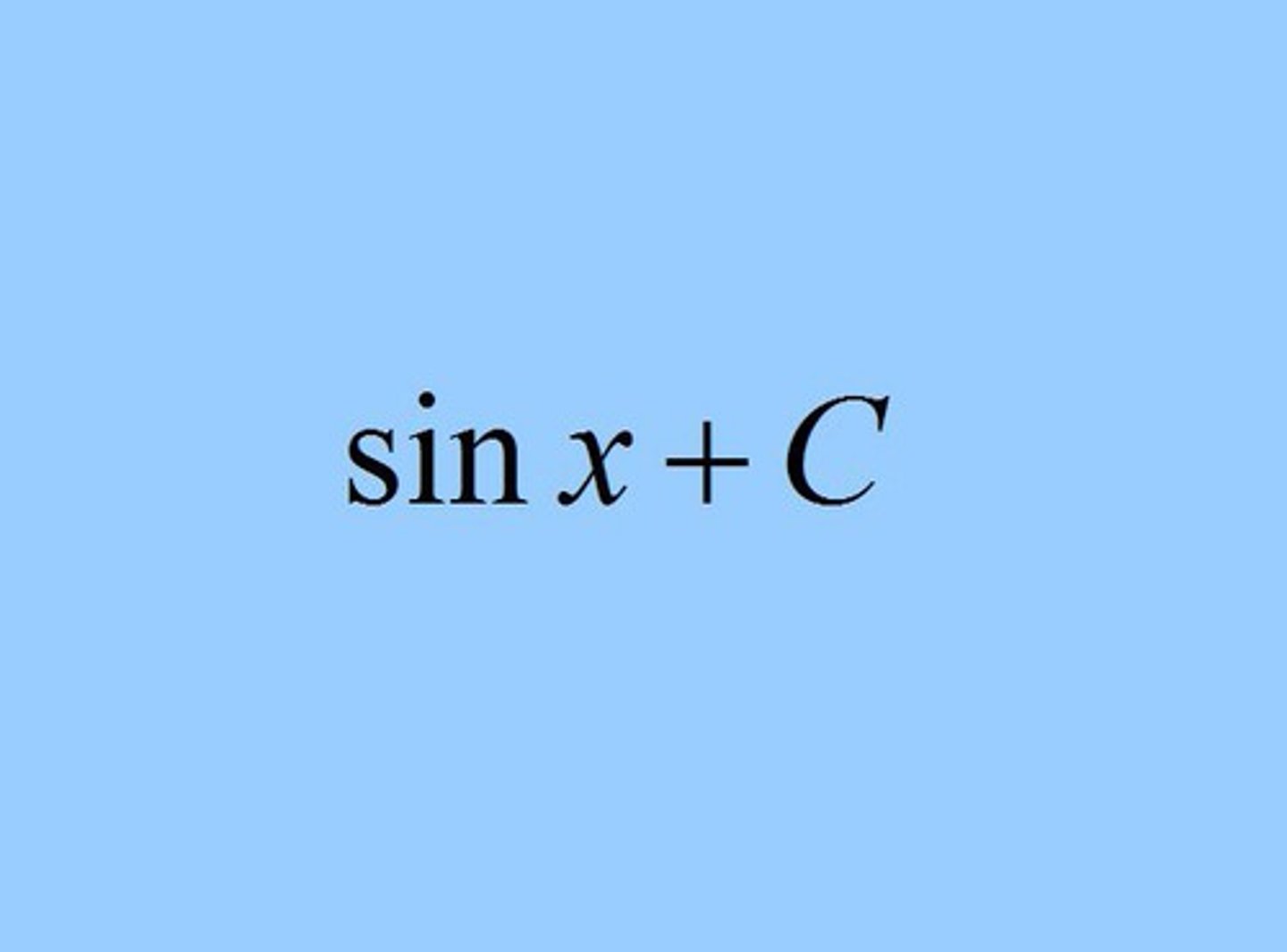
∫ sec² x dx =

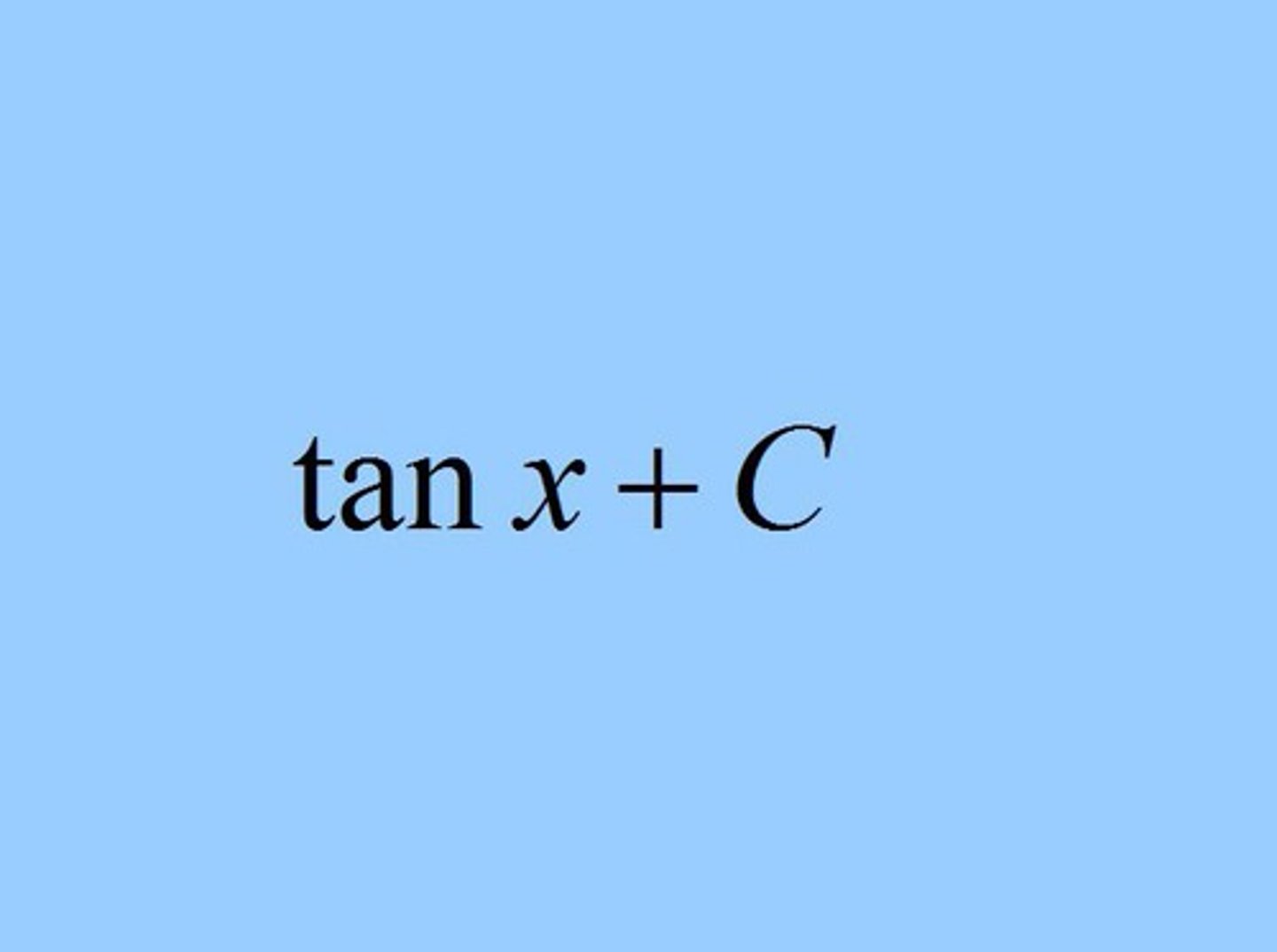
∫ a ^ x dx =

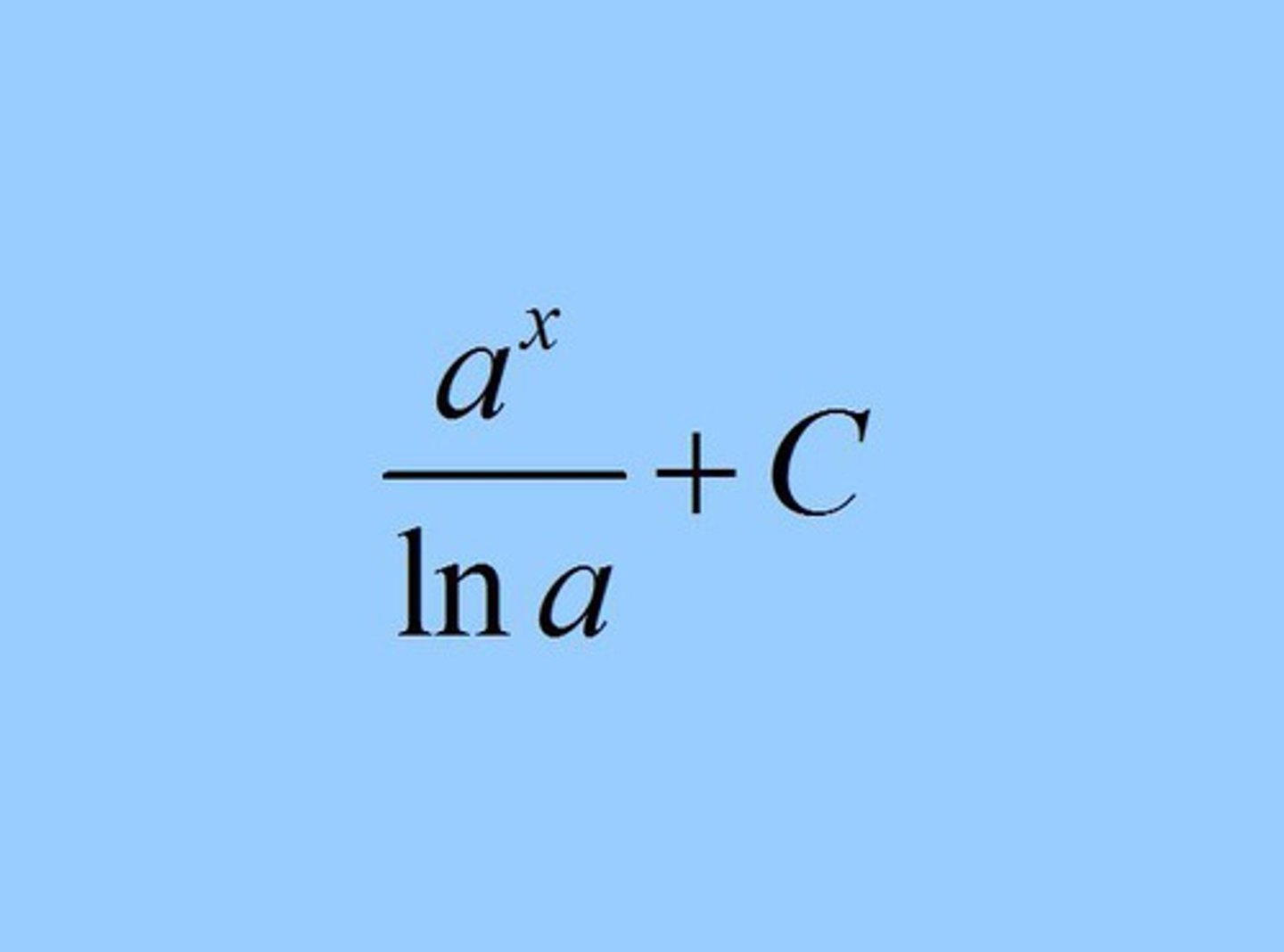
∫ tan x dx =

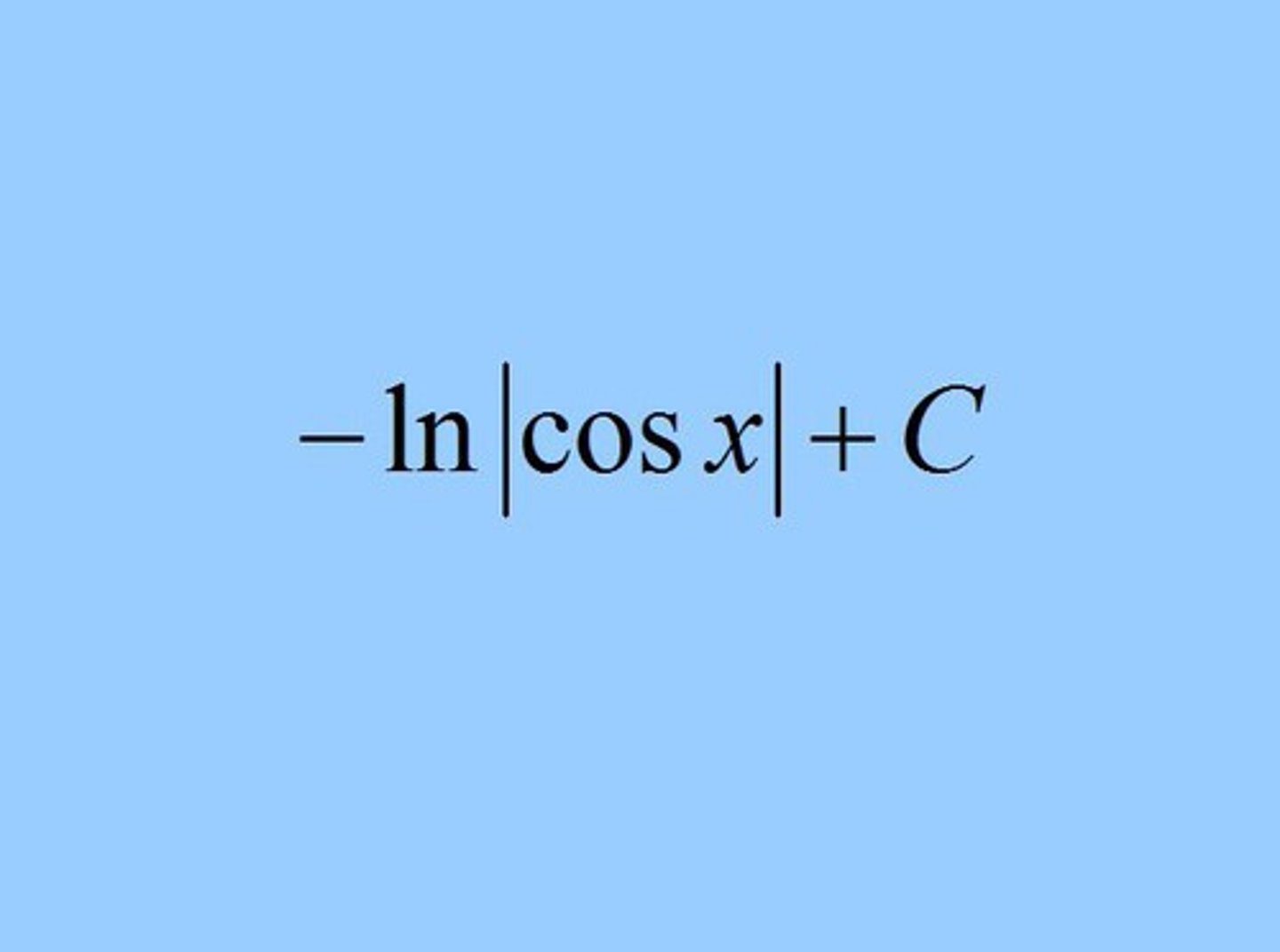
∫ 1 / (x² + 1) dx =

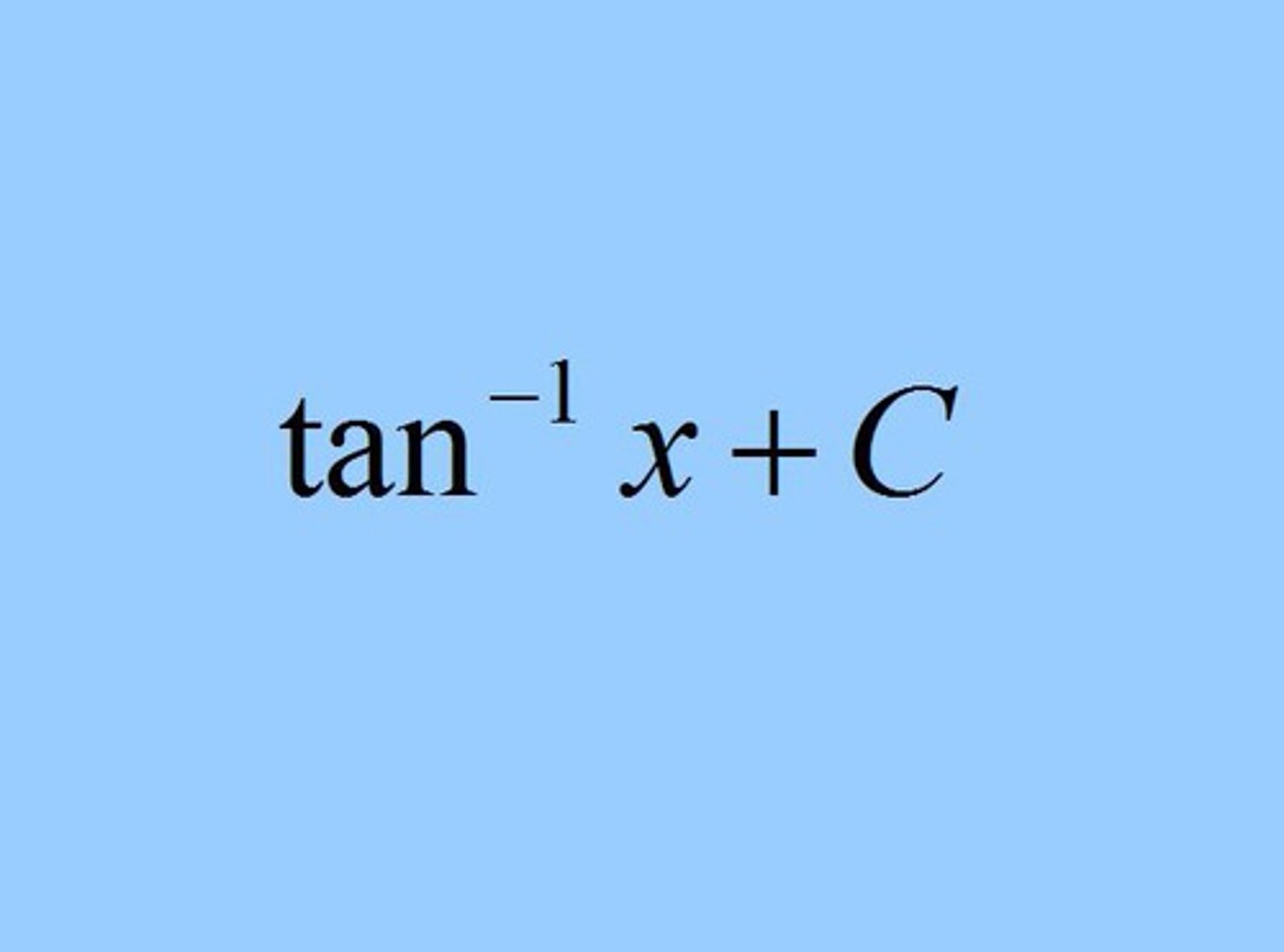
∫ 1 / √(1 - x² ) dx =

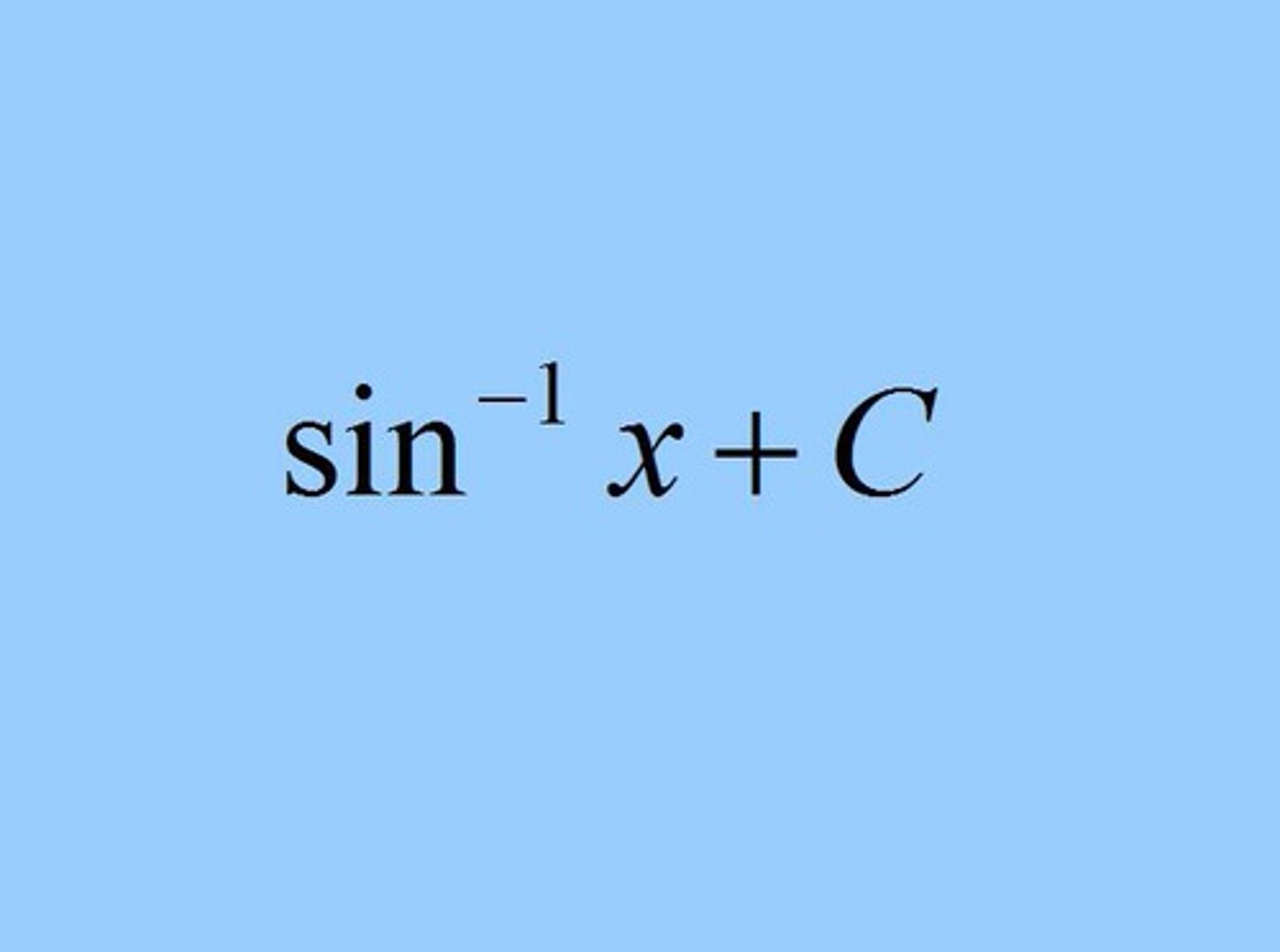
The average value of f from x = a to x = b

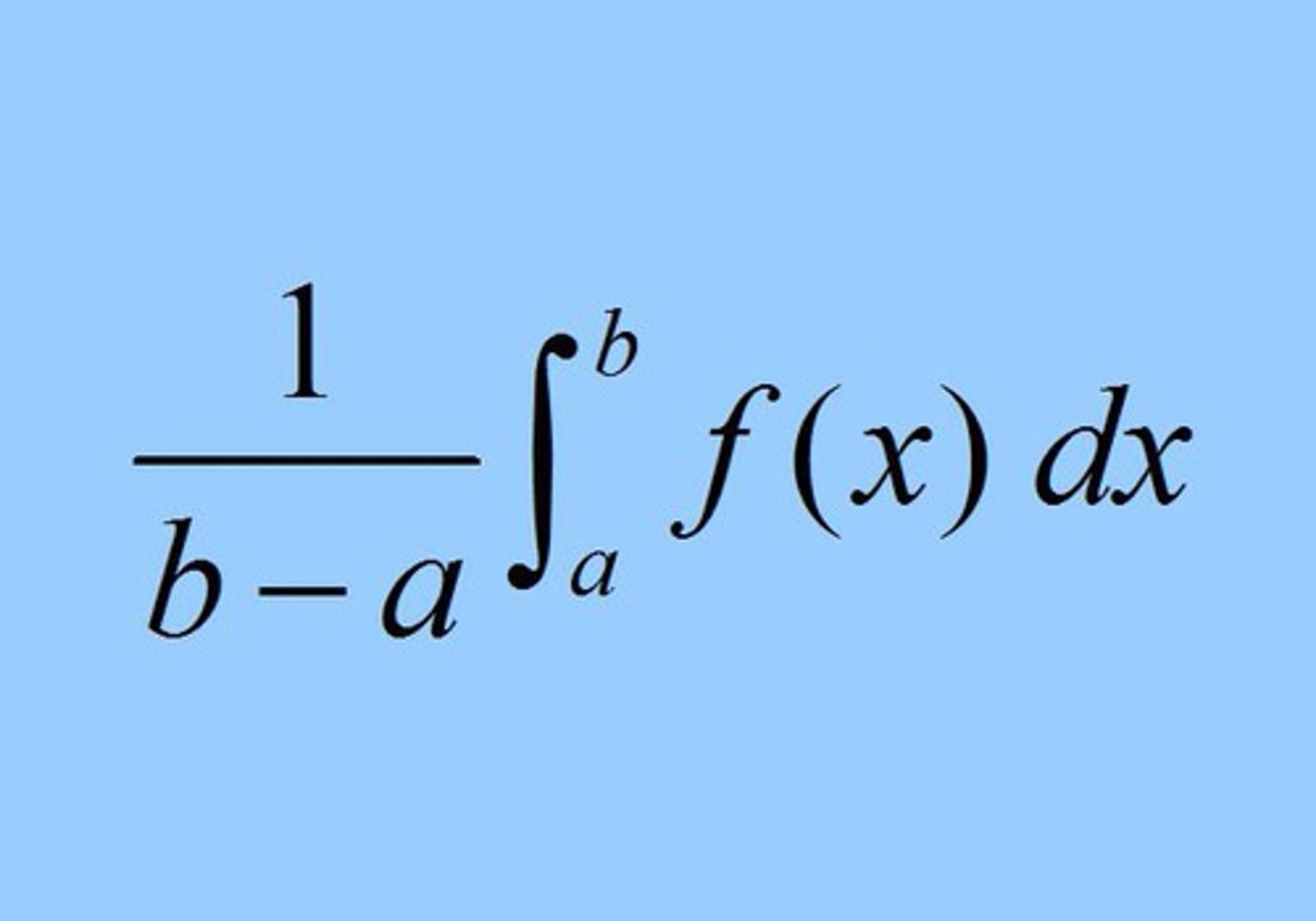
Adding adjacent integrals

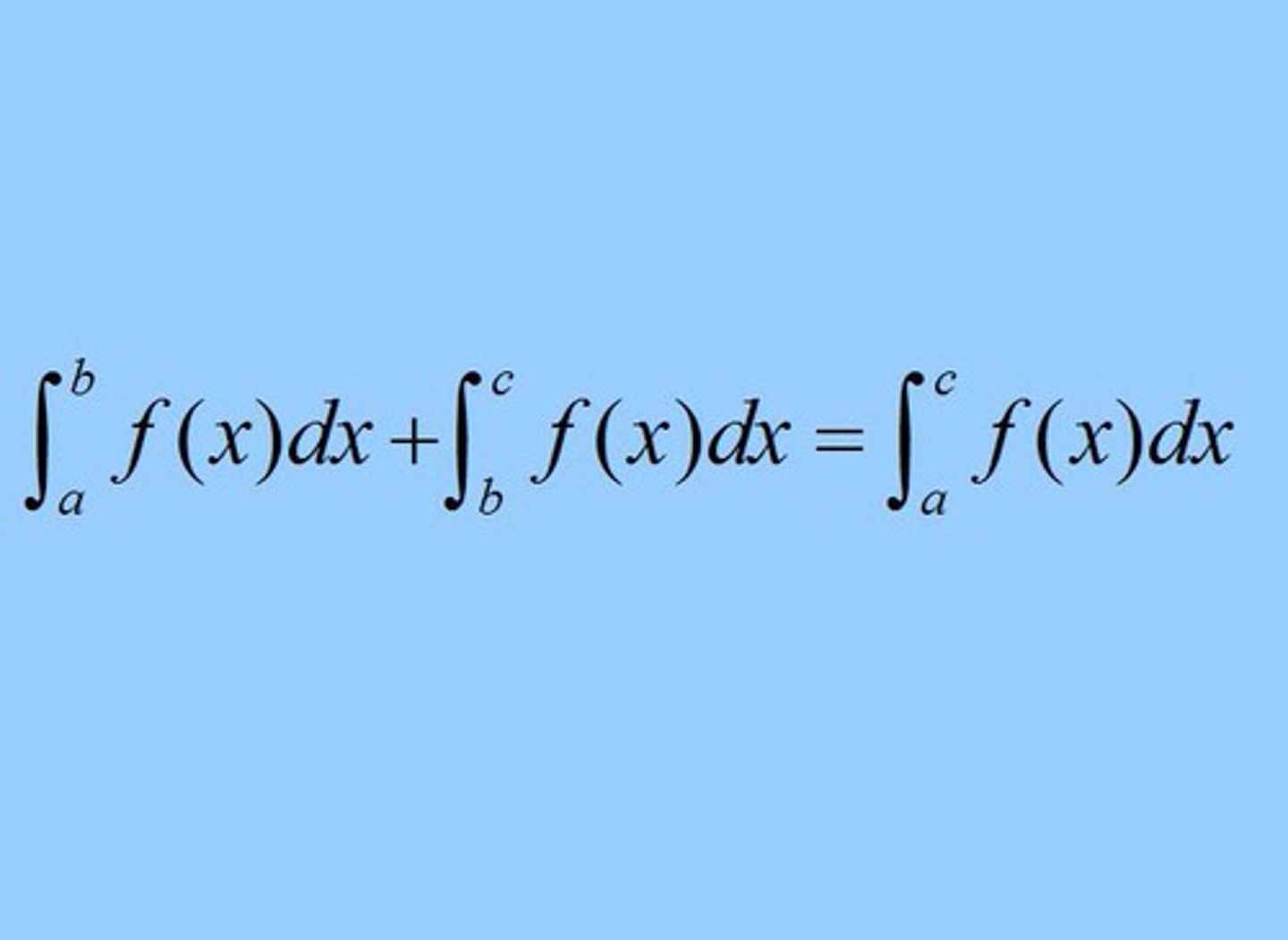
Swapping the bounds of an integral

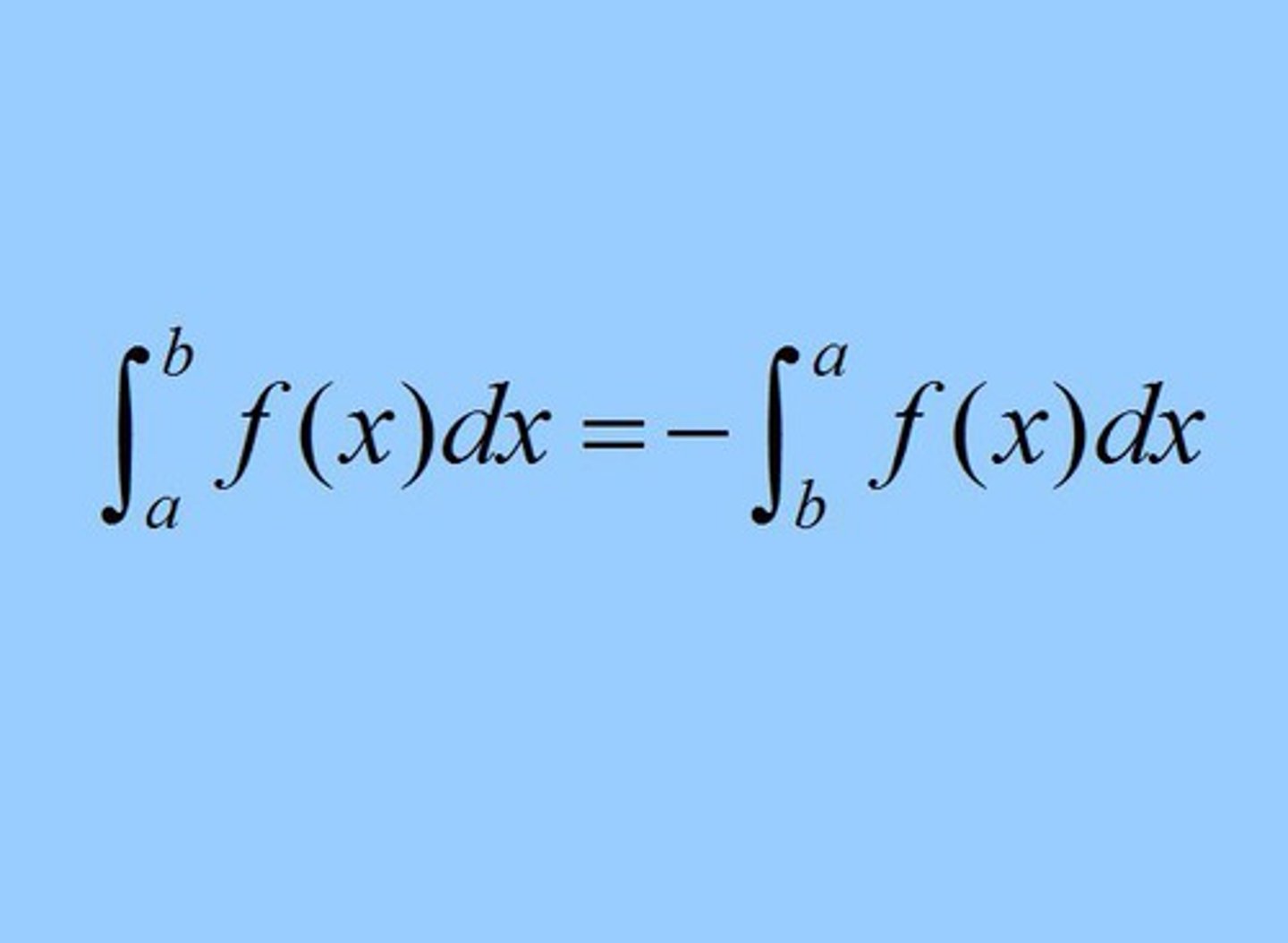
Exponential Growth

Solution of

dy/dt = kP

P(0) = P₀

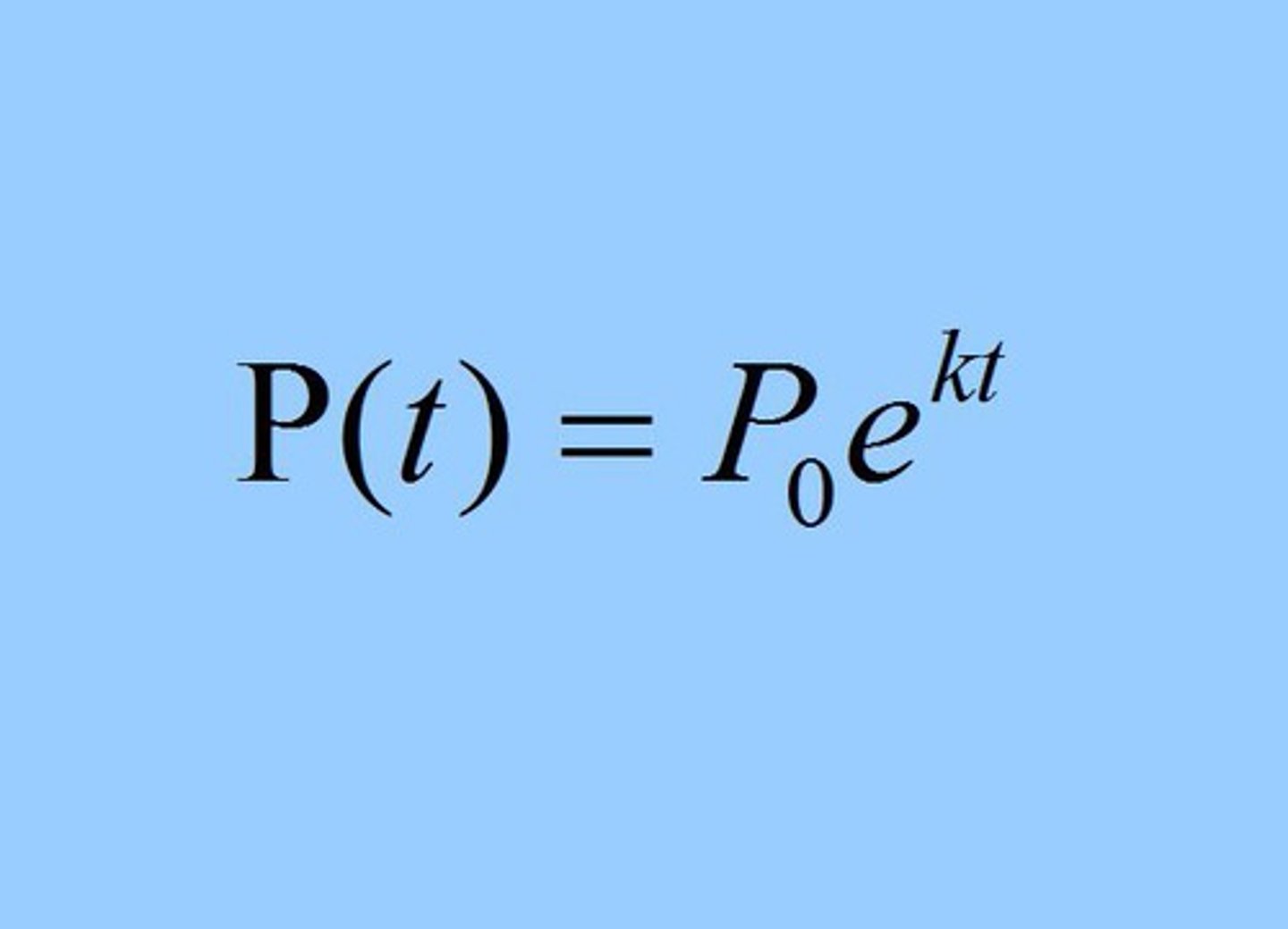
Steps to solve a differential equation

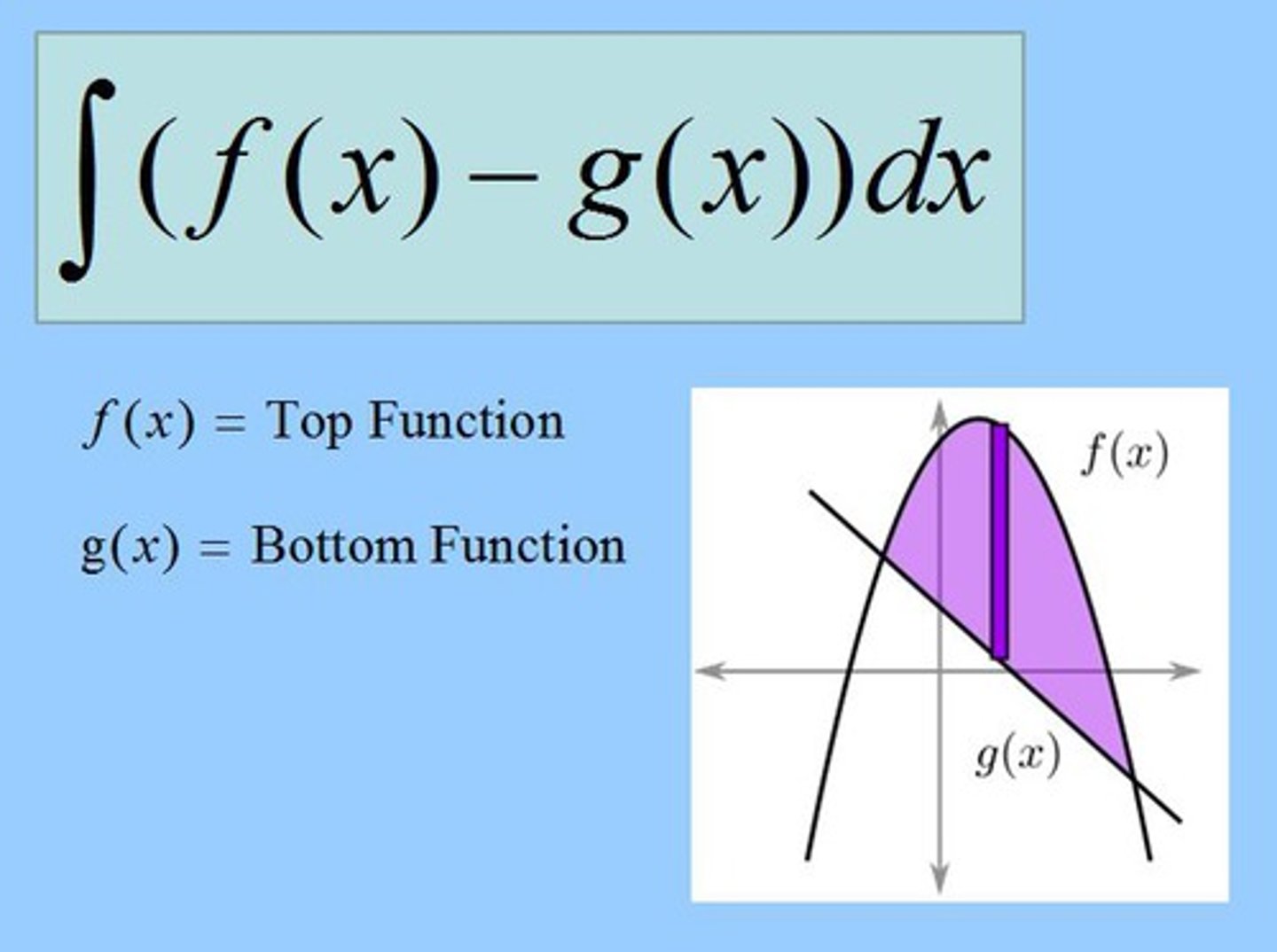
To find the area between 2 curves using vertical rectangles (dx)

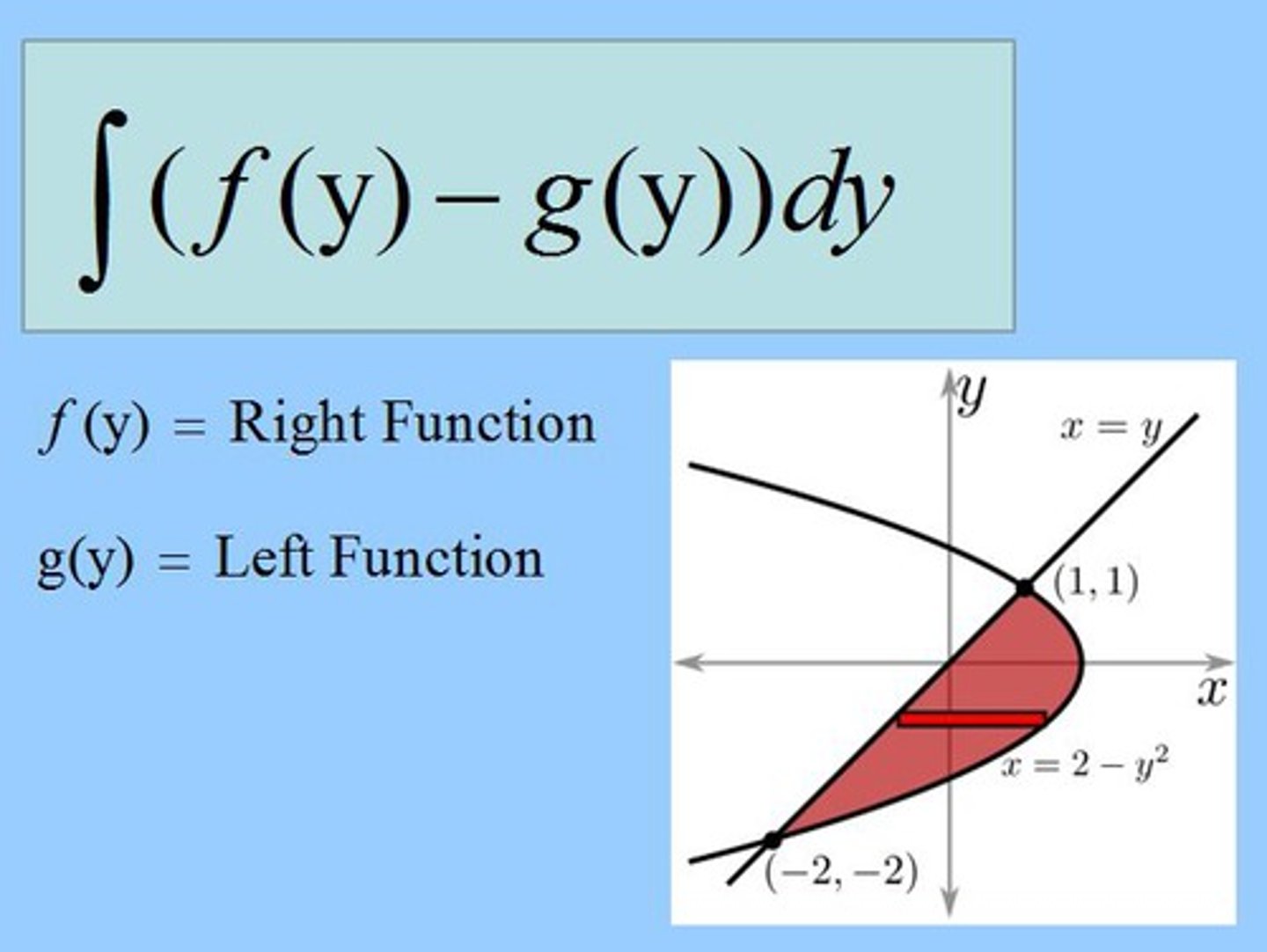
To find the area between 2 curves using horizontal rectangles (dy)