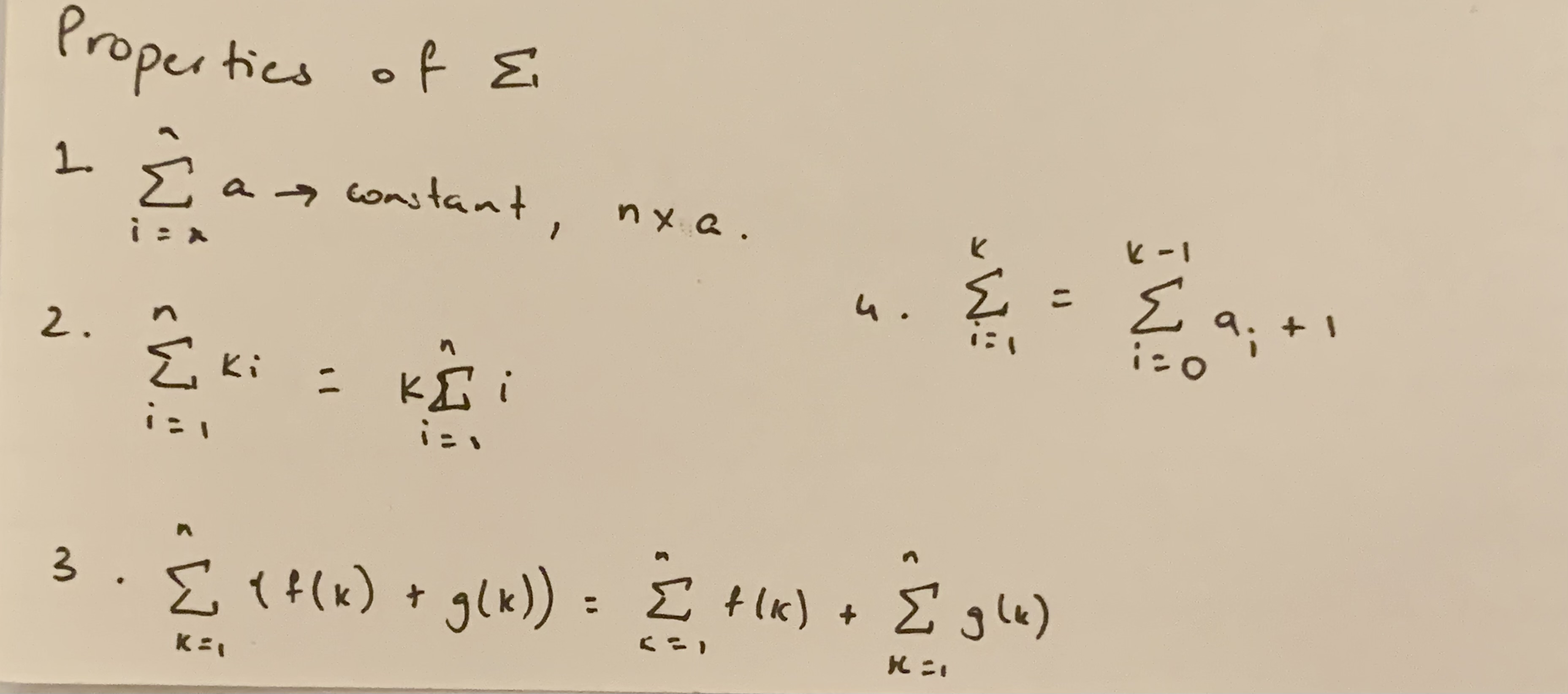Sequences and Series

Explicit definition

used to find any term (nth term) of the arithmetic sequence, a1, a2, a3, ..., an,.... using its first term (a) and the common difference (d). This formula gives the nth term formula of an arithmetic sequence.

Recursive definition

a formula that defines any term of a sequence in terms of its preceding term(s).

-Arithmetic sequence:
-nth term:
-Sum of terms:

-an ordered set of numbers that have a common difference between each consecutive term

-an=a1+(n−1)d
-Sn= n/2[2a+(n-1)d]

-Arithmetic series:
-Gaus’ addition:

-the sum of the terms in an arithmetic sequence with a definite number of terms.
-(1st term+last term)(total no.of terms/2)

Arithmetic mean:

-sum of values/no.of values

Approximating Arithmetic sequences

Average x n (position of term)

Geometric sequence

an ordered set of numbers that progresses by multiplying or dividing each term by a common ratio

Geometric series

the sum of the terms in a geometric sequence

Geometric mean

Infinite geometric series (sum)

the sum of an infinite geometric sequence

common difference (a)

d= an/an-1

common ratio ( r)

r= u3/u2

Compound interest

FV=PV (1+r/100k)^kn

k values
yearly:
half-yearly (or semianually):
monthly:
Quaterly:

yearly: 1
half-yearly (or semianually): 6
monthly: 12
Quaterly: 4

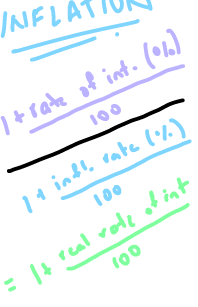
Finding real value of interest formula

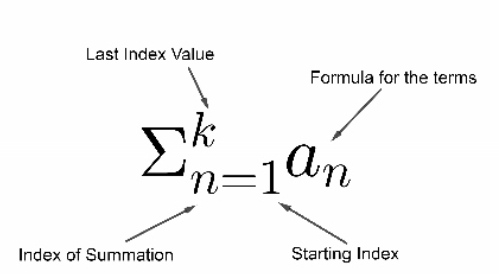
Sigma notation

Finding geometric mean between terms

1. Find the r using the first and last term

2. substitute to find the terms [u1r^n-1=Un]

Finding the greatest value of n

solve inequality based on the given value
eg. u1r^n-1<200

Finding the no.of terms

1. Identify the position of the last term

2. Find n [an=a+(n-1)d

Checking to see if the term is in the sequence

Substitute the term with Un or an

Properties of Sigma notation