Multi Vector quiz 1

vector forms

arrow: PQ (with line on top)

component form= <v1,v2>

linear combo / standard unit vectors ( v=-4i+7j-2k)

vector = <terminal point - initial point>

Norm / Magnitude of vector

√(terminal - initial)² = √(v1² +v2²)

vector addition, scalar multiple, negative, and difference

u+v = <u1+v1, u2+v2>

cu = c<u1,u2> = <cu1,cu2> *c is a constant, not vector

-v = -<v1,v2> = <v1,-v2>

u-v = <u1-v1, u2-v2>

unit vector

u = v / ||v||

u= component form / magnitude

check by seeing if end result has a magnitude of 1 with square root

parallel vectors

parallel when u = cv where c is a scalar

collinear vectors

share a starting point and parallel

dot product

u\cdot v = u1v1+u2v2+u3v3

angle between two vectors

cos theta = ( u\cdot v ) / (||u|| ||v||)

cos theta = dot product / magnitudes multiplied

angle if u*v

<0

=0

>0

<0 is obtuse (from pi/2 to pi)

=0 is right (pi/2)

>0 is acute (from 0 to pi/2)

orthagonal vectors

orthagonal /perpendicular when

u * v = 0

projection of u onto vector v

u = w1 + w2 (horizontal and vertical components)

w1 parallel to v (but not always same direction) and w2 orthagonal

w1 = proj_v u =( (u*v) / ||v||² ) v

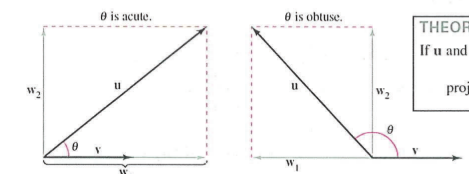
vector component of u orthogonal to v

u - w1

or

u - proj_v u

3d coords

• 3 axes

• 8 octants

• 12 right angles

distance formula, midpoint, sphere

distance: √( (△x)² + (△y)² + (△z)² )

midpoint: (x1+x2)/2 , (y1+y2) / 2 , (z1+z2) / 2

sphere: (△x)² + (△y)² + (△z)² = r²

cross product method

u x v

2 by 2 determinant : (ad - bc)

ab

cd

determinant i - determinant j + determinant k

cross product geometric properties

u x v is othagonal/perpendicular to both u and v

||u x v|| =||u|| ||v|| sin theta = area of parrelogram having u and v as adjacent sides

u x v = 0 if and only if u and v are scalar multiples

height of rectangle would be ||v|| sin theta

area of triangle formed by vectors: ||u x v || / 2

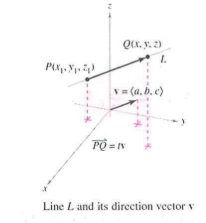
Lines in 3D

Need a direction vector v and a starting point P (x,y,z)

line L is all points Q(x,y,z) for which vector PQ is parallel to direction vector v <a,b,c>

*PQ is a scalar multiple of v

parametric equations of a line 3D

x = x1 + at

y = y1+ bt

z = z1 + ct

vector form

<x,y,z> = <x1,y1,z1> + t<a,b,c>

vector form = <vector of a point> + t <direction vector>

three symmetric equations of line (if all vector comps of v are nonzero)

(x-x1)/a = (y-y1)/b = (z-z1)/c

*isolate t in parametric equations, and set all equal to each other

distance between a point and a line in space

D = ||PQ x u|| / ||u||

u is a direction vector, P is point on the line

*also equivalent to ||PQ|| sin theta (height of earlier rectangle)

Distance = magnitude of the cross product

Equation of a plane in space

plane contains point (x1,y1,z1) and normal vector n=<a,b,c>

standard form: a(x-x1)+b(y-y1)+c(z-z1)=0

*normal vector from cross product sometimes

angle between two planes

cos theta = |n1 * n2| / ( ||n1|| ||n2|| )

normal vector dot product = 0 then planes are orthogonal/perpendicular

normal vectors are scalar then planes are parallel

parametric line of intersection

Write parametric equations in terms of one another to isolate variables.

Set one as t, and get other t with that term.

Find the parametric equations as x=, y=, z=

for a point, plug in x,y,z to og parametric, solve for exact t, and plugin

distance between a point and a plane

D = ||Proj_n PQ|| = |PQ * n| / ||n||

where n is the normal vector

projection of s onto plane

s - N

s -proj_n s