[AP Calc] Unit 9: Series and Sequences
5.0(3)Studied by 97 people
0%Unit Mastery
0%Exam Mastery
Build your Mastery score
Multiple Choice
Call KaiSupplemental Materials
Card Sorting
1/15
Last updated 6:59 PM on 1/30/23
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
16 Terms
1
New cards
partial sum
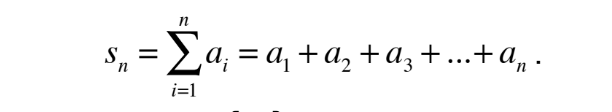
2
New cards
geometric series
|r|
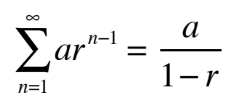
3
New cards
harmonic series
always divergent
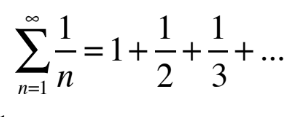
4
New cards
test for divergence
if the lim(a) DNE or lim(a)≠0 → the series is divergent
5
New cards
integral test
only used if the function is continuous, positive, and decreasing
take the integral, then the limit
take the integral, then the limit
6
New cards
p-series
p>1; convergent
p≤1; divergent
p≤1; divergent
7
New cards
remainder estimate for the integral test
where is f continuous, positive, and decreasing for x≥n and Σa is convergent
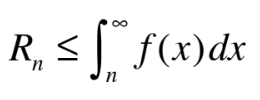
8
New cards
comparison test
if Σa and Σb are series with positive terms
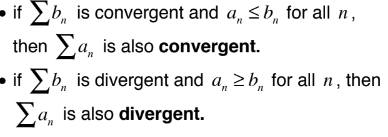
9
New cards
limit comparison test
where c is positive and finite and Σa and Σb are series with positive terms
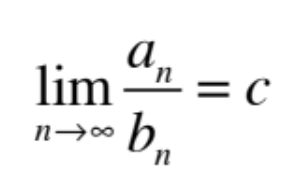
10
New cards
alternating series
a series whose terms alternate from positive to negative
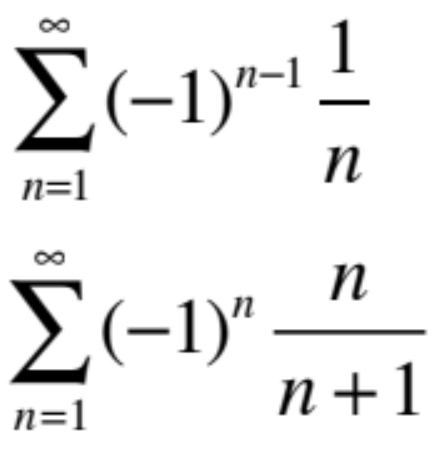
11
New cards
alternating series test
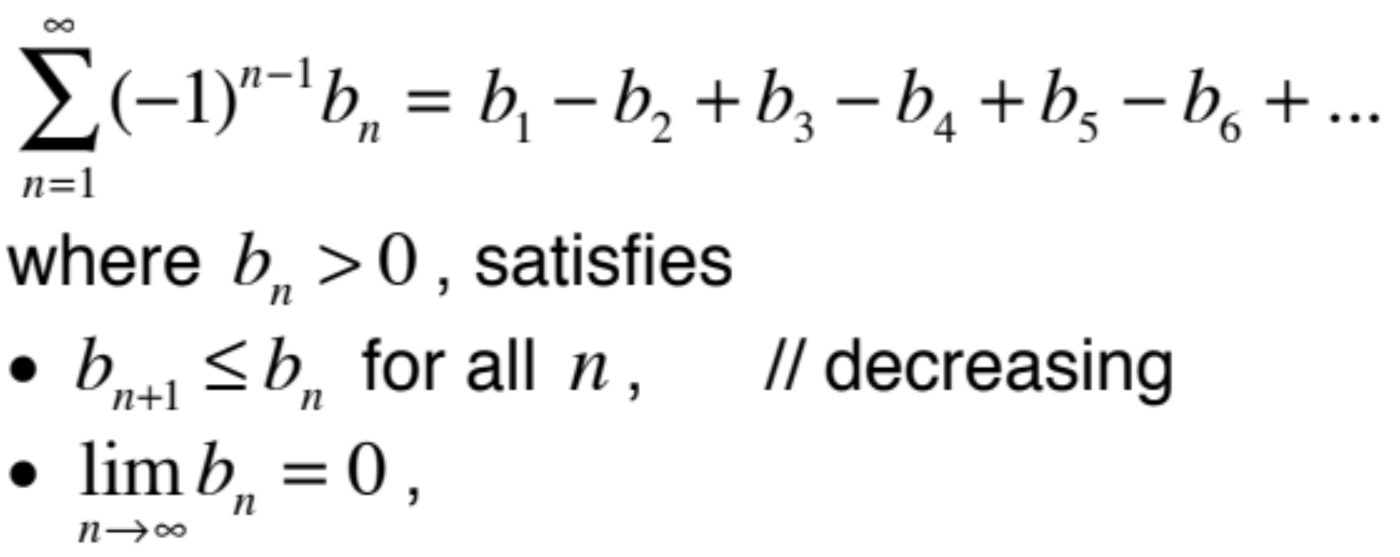
12
New cards
alternating series error bound theorem
13
New cards
absolutely convergent
a series, Σa, is ______ if Σ|a| is convergent
14
New cards
conditionally convergent
a series, Σa, is ______ if Σ|a| is divergent
15
New cards
ratio test
16
New cards
root test
