Introduction to Graphs: Vertices, Edges, and Applications in Data Structures Cartes | Quizlet

Graph

A data structure for representing connections among items, consisting of vertices connected by edges.

Vertex

Represents an item in a graph.

Edge

Represents a connection between two vertices in a graph.

Adjacency

Two vertices are adjacent if connected by an edge.

Path

A sequence of edges leading from a source (starting) vertex to a destination (ending) vertex.

Path Length

The number of edges in the path.

Distance

The number of edges on the shortest path between two vertices.

Number of Vertices (V)

The total count of vertices in a graph.

Number of Edges (E)

The total count of edges in a graph.

Maximum Number of Edges

Given 4 vertices A, B, C, and D and at most one edge between a vertex pair, the maximum number of edges is 6.

Computer Network Graph

A graph that represents connections among computers and servers.

Social Network Graph

A graph that represents friendships among people.

Example of Vertices in a Computer Network

PC1, PC2, Server1, Server2, and Server3.

Example of Edges in a Computer Network

Connections include PC1 to Server1, PC1 to Server2, Server1 to Server2, Server1 to Server3, Server2 to PC2, and Server3 to PC2.

Friendship in Social Network

Raj and Maya are friends, but Raj and Jen are not.

Can a Vertex Have More Than One Edge?

Yes.

Can an Edge Connect More Than Two Vertices?

No.

Are Maya and Thuy Friends?

No.

Computer Network Graph Vertices Count

5

Computer Network Graph Edges Count

6

Shortest Path from PC1 to PC2

e2, e5.

Distance from PC1 to PC2

2

Adjacent Vertices

Two vertices are adjacent if connected by an edge.

Vertex Distance

Vertex distance is the length of the shortest path.

Shortest Path

The shortest path from PC1 to PC2 is e2, e5.

Graph Representation

Graphs are often used to represent a geographic map, which can contain information about places and travel routes.

Vertices in Graphs

Vertices in a graph can represent airports, with edges representing available flights.

Edge Weights

Edge weights in such graphs often represent the length of a travel route, either in total distance or expected time taken to navigate the route.

Travel Time Assignment

A map service with access to real-time traffic information can assign travel times to road segments.

Driving Directions

Driving directions use graphs and shortest path algorithms to determine the best route from start to destination.

Total Travel Time

Total travel time = 28 min.

Graph Edges and Vertices

Each street is a graph edge and each intersection a vertex.

Graph Example

A Street, B Street, C Street, 4th Street, Diagonal Street, House Road, 3rd Street, 2nd Street, 1st Street, and an unlabeled street connecting 1st Street to the Beach.

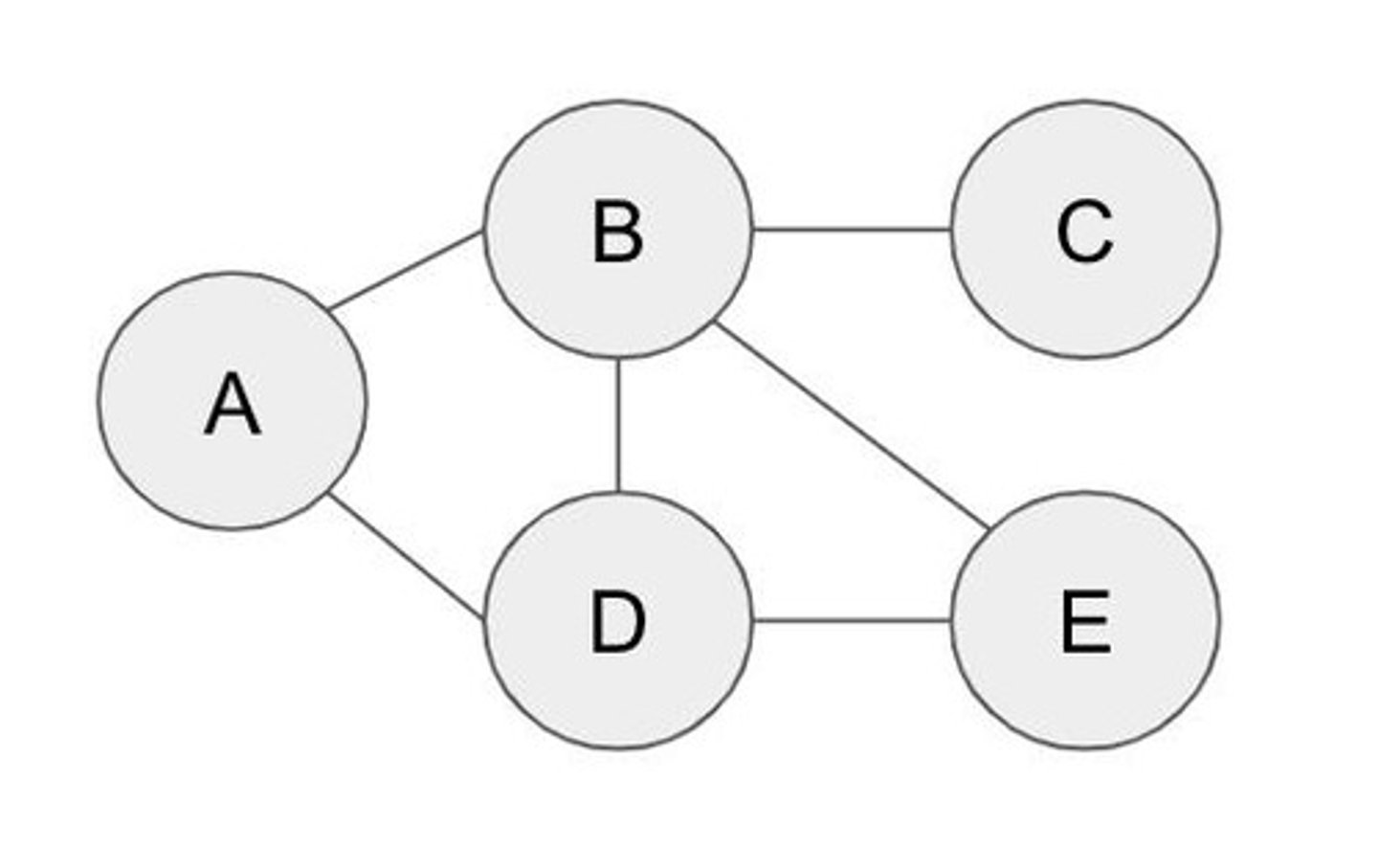
Path from B to G

Which of the following is a path from B to G? e3, e7; e1, e3, e7; No path from B to G.

Distance from D to C

What is the distance from D to C? 3, 4, 5.

PC1 and Server1

PC1 and Server1 are adjacent.

PC1 and Server3

PC1 and Server3 are not adjacent.

Vertices

House, Beach, Intersection of 4th Street and A Street, Intersection of Diagonal and A Street, Intersection of 2nd Street and A Street, Intersection of 1st Street and A Street, Intersection of Diagonal Street and B Street, Intersection of 3rd Street and B Street, Intersection of 2nd Street and B Street, Intersection of 1st Street and B Street, Intersection of Diagonal Street and C Street, Intersection of House Road and C Street, Intersection of 3rd Street and C Street, Intersection of 2nd Street and C Street, intersection of 1st street and the road to the beach.

Travel Time

Sections of roads between vertices have weights labeled as travel time, in minutes.

5 min

Travel time from intersection of 2nd Street and A Street to intersection of 1st Street and A Street.

9 min

Travel time from intersection of 4th Street and A Street to intersection of Diagonal Street and A Street.

10 min

Travel time from intersection of Diagonal Street and A Street to intersection of 2nd Street and A Street.

2 min

Travel time from intersection of 3rd Street and B Street to intersection of 2nd Street and B Street.

7 min

Travel time from intersection of 2nd Street and A Street to intersection of 2nd Street and B Street.

6 min

Travel time from intersection of Diagonal Street and B Street to intersection of Diagonal Street and C Street.

3 min

Travel time from intersection of 3rd Street and B Street to intersection of 3rd Street and C Street.

4 min

Travel time from intersection of 2nd Street and B Street to intersection of 1st Street and B Street.

1 min

Travel time from intersection of House Road and C Street to the house itself.

Road Map Representation

A road map can be represented by a graph. Each intersection of roads is a vertex. Destinations like the beach or a house are also vertices.

Edges

Roads between vertices are edges.

True/False Statement 1

The longer a street is, the more vertices will be needed to represent that street.

True/False Statement 2

When using the physical distance between vertices as edge weights, a shortest path algorithm finds the fastest route of travel.

True/False Statement 3

Navigation software would have no need to place a vertex on a road in a location where the road does not intersect any other roads.

True/False Statement 4

If navigation software uses GPS to automatically determine the start location for a route, the vertex closest to the GPS coordinates can be used as the starting vertex.

Flight delays

Factors that may change the weight of an edge connecting two airport vertices.

Weather conditions

Factors that may change the weight of an edge connecting two airport vertices.

Flight cost

Factors that may change the weight of an edge connecting two airport vertices.

Graph of product relationships

Can be used to produce recommendations based on purchase history.

Game console

A product purchased by a customer that is represented in the graph.

Dishwashing soap

A product purchased by a customer that is represented in the graph.

Television 1

A product purchased by a customer that is represented in the graph.

Television 2

A product purchased by a customer that is represented in the graph.

Game console game 1

A product to recommend to the customer.

Game console game 2

A product to recommend to the customer.

Game console game 3

A product to recommend to the customer.

Tablet computer

A product purchased by a customer that is represented in the graph.

Blender

A product purchased by a customer that is represented in the graph.

Kitchen towels

A product purchased by a customer that is represented in the graph.

Oven mitts

A product purchased by a customer that is represented in the graph.

Muffin pan

A product purchased by a customer that is represented in the graph.

Muffin mix

A product purchased by a customer that is represented in the graph.

Secondary recommendations

Include all products adjacent to recommended products.

Product recommendations

Based on the customer's purchase history.

Largest number of recommendations

Produced by purchasing a game console.

Professional network graph

A graph where edges commonly represent business conducted between people.

Adjacency list

A common approach for representing a graph where each vertex has a list of adjacent vertices.

Graph with 14 vertices and 17 edges

A specific graph representation that includes 14 vertices and 17 edges.

Graph with 14 vertices and 16 edges

A specific graph representation that includes 14 vertices and 16 edges.

Business connection

A relationship represented by an edge in a professional network graph.

Participation Activity 9.2.6

Professional networks represented by graphs help people establish business connections.

Participation Activity 9.2.7

Refers to the animation's graph representing the professional network.

Who has conducted business with Eusebio?

Giovanna, Manuel, Keira.

Best person to introduce Octavio to Wilford

Shayla, Natasha, Manuel, Rita.

Length of the shortest path between Salvatore and Reva

5, 6, 7.

Graph with four vertices

A graph that includes vertices A, B, C, and D.

Edges in a graph with four vertices

A to B, A to C, B to C, and B to D.

Step 1 in professional network graph

Vertices represent people and edges represent a business connection.

Step 2 in professional network graph

Tuyet conducts business with Wilford, adding a new edge in the graph.

Step 3 in professional network graph

The graph can help professionals find new connections.

Static figure of a graph

A visual representation of a graph showing vertices and edges.

Vertices in the graph

Rita, Octavio, Reva, Wilford, Manuel, Tuyet, Shayla, Cyrus, Eusebio, Keira, Giovanna, Salvatore, Bruno, and Alona.

Edges in the graph

Connections between vertices that represent relationships.

Mutual contact

A person who connects two others in a network.

Sparse Graph

A graph that has far fewer edges than the maximum possible.

O(V + E)

The size of an adjacency list graph representation, where V is the number of vertices and E is the number of edges.

Adjacency Matrix

A representation of a graph where each vertex is assigned to a matrix row and column, with a matrix element of 1 if there is an edge between the vertices.

Direct Bus Route

A bus route that connects two locations directly without any stops.

Minimum Number of Buses

The least number of buses required to travel between two locations.

Graph Data Structure

A data structure that consists of a set of vertices and edges.

Matrix Element

An entry in a matrix that indicates the relationship between two vertices.