Radiation Interactions With Matter, Units, and Decay

3 broad categories of radiation interactions

1. Ionization - removing bound electrons.

2. Excitation - exciting bound electrons.

3. Nuclear - interactions involving a nuclear change.

Raleigh Scattering

1. This is a function of the wave nature of light.

2. It is of little concern in radiation therapy.

3. Occurs for very low-energy photons.

4. The electric field of a photon causes an electron to oscillate (absorbs the energy) which is then re-irradiated in another direction (scattered) with no change in energy.

Raleigh Scattering interaction probability per unit mass

Z/E²

Photoelectric effect interaction probability per unit mass

.

Photoelectric effect

1. This is a function of the particle nature of light.

2. A photon interacts with an electron on an inner shell where it is completely absorbed and the electron is ejected.

3. This leaves a vacancy in the shell that is filled when an electron from a higher level drops.

4. When an electron drops from a higher energy to a lower energy state, it emits a photon equal to the binding energy difference between the energy levels.  This is called a characteristic x-ray as it is specific to the atom’s unique energy levels (a fingerprint) and can be used in spectroscopy to identify the atom in question.

5. If we consider the ejected electron, it has an energy (E): 

   

1.  - is the incident photon energy.

2.  - is the binding energy of the electron.

4. Sometimes a characteristic x-ray will interact with another bound electron and be absorbed ejecting that electron which is called an Auger electron (pronounced “o-jay” electron).

compton scattering

1. This is a function of the particle nature of light.

2. It occurs when a photon interacts with an outer shell electron and is scattered through some angle ejecting the electron who has an energy related to the scattering angle by the following equation.

compton scattering equation for scattered photon E

Generalizations for compton scattering at 90/180

1. Photons scattered at 90^o (side-scatter) is approximately independent of energy with a maximum of 0.511 MeV.

2. Photons scattered at 180^o (backscatter) is approximately independent of energy with a maximum of 0.255 MeV.

3. Radiation scattered between these angles will have a maximum energy that falls between these energies.

compton scattering interaction probability

approx 1/E

pair production

1. It occurs when a photon passes near a nucleus of an atom and an electron and positron pair are created.

2. It has a minimum threshold for occurrence of 1.022 MeV (the rest mass of an electron and positron together).

3. Any energy possessed by the photon in excess of 1.022 MeV is converted to kinetic energy which is distributed between the created positron and electron and usually sends them in the same direction as the incident photon.

pair production interaction probability per unit mass

Zln(E)

• Pair production is more probable than Compton interactions above 25 MeV in tissue.

Photonuclear interactions

1. For very high energy photons, (threshold at about 8 MeV) photons can interact with a nucleus and eject neutrons (photodisintegration).

1. The threshold is about 8 MeV but it is exceedingly rare becoming more common by about 10 MeV.

2. This is why for high energy LINACs, neutron shielding is important.

Charged Particle interactions per unit mass for a given medium are roughly proportional to:

C²/v²

• C is particles charge

• v is speed

• as a particle slows down its rate of energy deposition increases rapidly.  This is called the Bragg Peak and occurs near the end of a charged particle's path.

• continuous slowing down approximation (CSDA) is often used as a shortcut for the approximate range of charged particles. In physical terms, it is the average energy loss per unit path length in a given medium. Therefore, when all the energy is expended, the particle is at its CSDA range.

proton interactions

1. Protons principally interact by ionizing atoms by knocking off electrons.

2. If they are of high enough energy they can reach the nucleus and create a new atom (such as in the creation of F-18 in a cyclotron).

3. Protons follow relatively straight paths due to their large size as compared with electrons (which they are principally interacting with) and exhibit a Bragg Peak near the end of their path.

4. The Bragg Peak is exploited for radiotherapy as it deposits an increased dose near the end of the proton’s path (which ideally is where the tumor is).

Beta Interactions

1. Beta particles can scatter off bound electrons and eject them in a method very similar to Compton interactions in photons.

1. Produces characteristic x-rays when vacancies are formed.

do electrons exhibit a bragg peak? do we see it?

yes but dont see it: electrons are scattering on electrons, and their random paths completely blur out the peak in a patient.

range straggling vs energy straggling

• Beta particles exhibit these phenomena due to their tortuous paths while traversing a material.  

• Each particle will present with different interaction histories which, in turn, yield variations in the energy of the particles at any given depth.  

  • This variation in energy is termed energy straggling.

•  Range straggling is directly related since, as the energy varies, the amount of penetrative power remaining also varies leading to a range of ranges being exhibited.

Bremsstrahlung

1. Electrons can be decelerated in the electric field of a nucleus so that they change direction and radiate a photon.

2. Photons are emitted with a huge spectrum up to the maximum energy of incident electrons (the average is about ⅓ the max energy).

3. This is very inefficient and only occurs about 1% of the time in the diagnostic energy range.  For therapeutic energies, the probability of bremsstrahlung production increases with the atomic number of the target, Z, and the energy of the incoming electrons.  However, due to the high energies involved in the therapeutic range, typically referenced efficiencies are on the order of 20-30%.

Alpha interactions

1. Alpha particles are large and have a +2 charge (relative to the charge of the electron) so they interact very strongly.

3. Alpha particles can ionize electrons or interact with the nucleus causing spontaneous or delayed radioactive decay.

neutron interactions: 2 main categories

1. Recoil reactions where the neutron hits a nucleus and sends it moving creating its own ionizations.

   1. When interacting with heavy particles neutrons lose very little energy (basically bounce off).

2. Nuclear activations:

   1. Since neutrons carry no charge they can easily reach a nucleus as electrons do not screen them with any repulsive forces due to charge.

   2. Neutrons can be absorbed into the nucleus and result in a spontaneous or delayed radioactive decay resulting in any number of particles (alphas, gammas, protons, other neutrons).

Photoelectric effect dominant energy range

dominant from 10-30 keV (significant from 10-70 keV).

compton dominant energy range

dominant from 30 keV to 25 MeV (significant almost everywhere).

pair production energy range

dominant above 25 MeV (significant around 10 MV).

Air Kerma Strength

1. more advanced unit of activity that is used for calculating dose from a source without first worrying about exposure from it.  It is specified as the air KERMA rate in free space at 1 meter from the source (units U; U = cGy*cm²/hr).

   1. Air Kerma Strength is dependent on the source type and is usually found using a NIST free in air chamber.

convert from air kerma strength to activity

1. 

2. for instance, for I-125 the conversion between mCi and U is:

   

Coulomb

this is a fundamental unit of charge as a single electron has a charge of 1.602x10-19 C (in 1 C there are 6.24x1018 electrons).

Exposure

this is sort of a generic unit and is equal to the amount of charge liberated per mass of dry air (units C/kg).

Roentgen

this is a special unit of exposure and is equal to 2.58x10-4 C/kg.

convert mCi to an exposure in Roentgens

rad

this is the amount of energy absorbed per unit mass (1 rad=100 erg/g).

how many rad in a Gy

1 Gy = 100 rad

exposure in Roentgens to Dose in Gray

1. in air: 

   

   .

2. for an MV beam in water/tissue: 

   

   .

3. the conversion between R and Gy is called the f-factor and is a ratio of the mass energy attenuation coefficients for photons.

 

Sievert

this is the equivalent dose delivered by radiation relative to photons (units J/kg).

rem (rem)

the equivalent dose delivered by radiation relative to photons (units: 1 rem = 100 erg/g).  Historically of note is that rem was an abbreviated term for Roentgen Equivalent Man.

rem in a sievert

1. 1 Sv = 100 rem

weighting factors for Gy to Sv

1. photons = 1

2. electrons = 1

3. neutrons = 5-20 (call it 10 for unknown energy)

4. protons -  5 (some discrepancy here with a range of 2-10 quoted with the NRC quoting 10 via 10CFR20)

5. alpha particles - 20

where do the Gy to Sv factors come from

10CFR20

Person-Sv

defined as the average dose received by a population multiplied by the number of people in that population.

half life

the time required for either the activity or the number of radioactive particles in a sample to decay to half of their original values 

.

mean life

1. effectively the average life-span of one of the members of a radioactive sample.

   

Cumulative Activity

when a radionuclide is implanted it is often useful to know the amount of activity given off by that sample over its entire lifetime.

transient equilibrium

1. This occurs when the parent half-life is only slightly larger than the progeny’s (by a factor of 10 or so).

2. In this case, the activity of the progeny (daughter) rises dramatically, and then matches the activity decline of the parent as the population of radioactive atoms in the progeny becomes dependent on being fed by the parent population.

3. Example: Mo-99 (half life 66 hours) decaying to Tc-99m

secular equilibrium

1. This occurs when the parent half-life is much greater than the progeny’s (by a factor of 1000 or so).

2. In this case, the daughter activity rises dramatically to meet the parent activity, but then attains a state of equal and dependent activity equilibrium.

3. Example: Ra-226 (half-life = 1600 years) decay to Rn-222 (half-life = 3.8 days).

No equilibrium conditions parent/daughter

1. This occurs if the daughter’s half-life is greater than the parent’s:

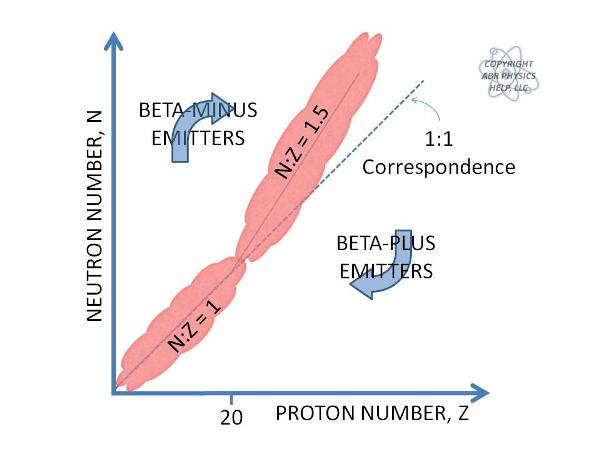
Draw the line of stability and indicate where its a beta minus vs beta plus emitter

1. In general, stable nuclides have an equal number of protons and neutrons.

2. However, as the Z increases the number of neutrons increases slightly.

   1. Protons repel each other and neutrons can be thought of as glue which holds the nucleus together (you need more glue as the repulsive force grows).

3. Nuclides attempt to return to the line of stability through an appropriate mode of radioactive decay.

Alpha decay: write out the decay terms

1. This decay consists of the emission of an alpha particle (which is equivalent to a Helium nucleus).

2. This generally only happens for atoms with atomic numbers greater than around 82.

3. From a specific nucleus, alpha particles are emitted in discrete energies (as opposed to a continuous spectrum of energies) and have large energies of about 5-10 MeV.

Beta minus decay equation and define

1. This decay occurs typically when the radioactive sample has a high neutron to proton ratio, therefore, lying above the line of stability.

2. The emission involves emitting a negatron causing the atomic number of the sample to increase by one while the mass number remains the same.

3. Also emitted, in addition to the negatron, is an antineutrino and some amount of disintegration energy.

4. Note that there will be a continuous spectrum of energies for the negatrons.

Beta plus decay equation and define

1. This decay occurs when the radioactive sample has a low neutron to proton ratio (below the line of stability).

2. The emission involves emitting a positron causing the atomic number of the sample to decrease by one while the mass number remains the same.

3. Also emitting, in addition to the positron, is a neutrino and some amount of disintegration energy.

4. Note that there will be a continuous spectrum of energies for the positrons.

5. Has a threshold of 1.022 MeV (rest mass of two electrons) for energy conservation.

Electron Capture

1. This process occurs when one of the orbital electrons is “captured” by the nucleus causing one of the protons to change state to a neutron.

2. Emitted from this is a neutrino and some amount of disintegration energy.

3. Note that the capturing of the inner shell electron (which is most probable) will leave a vacancy in the inner shell meaning that an outer shell electron will fall to the more stable state in the inner shell and characteristics x-rays and/or Auger electrons can be emitted.

4. This process competes with positron decay when there is not enough energy to fulfill positron emission’s threshold of 1.022 MeV.

Internal conversion

5. 

1. In internal conversion, some amount of energy from a de-exciting nucleus can be transferred to an orbital electron causing it to be ejected from the atom (think of it as analogously the photoelectric effect).

2. This process will also leave a vacancy that can result in the emission of characteristic x-rays and/or Auger electrons.

Isomeric transition

1. This is how a nucleus in an excited metastable state decays (e.g. Tc-99m).

2. A gamma ray is released and the nucleus type remains unchanged.

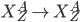
Photodisintegration

1. The interaction of a high-energy photon with a nucleus can cause the emission of a nucleon.  This can be either a proton or a neutron or even multiple nucleons.

2. The nomenclature for photo disintegration events are often given as, for example, gamma,p if the result is a gamma ray interacting with a nucleus and the following de-excitation results in the ejection of a proton.  Likewise, this would be labeled gamma ,n if the de-excitation from the excited state were to be accompanied with the ejection of a neutron

: 

Fission

1. In this process, we bombard a nucleus with neutrons which can cause the nucleus to split into nuclei of lower atomic number.

2. This usually only occurs for high Z materials (e.g. Uranium and Thorium).

Fusion

1. In this process, we combine two nuclei to form a nucleus with a larger atomic number.

2. This usually only occurs for low Z materials (e.g. Hydrogen and Helium).