chapter 11 - modern atomic theory

rutherford’s atoms

positive core with negatively charged electrons moving about it. nucleus is very small compared to atom so electrons make up rest of an atom

max Planck

discovered that atoms and molecules emit energy only in whole number multiples of certain well defined quantities

quanta

energy can be released only in certain definite amounts

plancks quantum theory/radiation

whcih is the emission and transmission through space of energy in the form of wave

wave

vibrating disturbance by which energy is transmitted

wavelength

is the distance between identical points on successive waves, usually expressed in units of m, cm, or nm

frequency

number of waves that pass through a particular point in one second, usually measured in units of hertz (Hz) (1Hz = S^-1)

amplitude

is the vertical distance from the midline of a wave to the peak or through

speed of a wave (u)

is given by the product of its wavelength and its frequency

photons

one can think of a beam of light traveling through space as a steam of tiny packets of energy

longer the wavelength of light

lower the energy

shorter the wavelength

higher the energy

common electromagnetic waves features

speed at which they travel, 3.00 × 10^-18 meters per second (m/s) or 186,000 miles per second, electromagnetic waves is c = frequency/wave length v

what does C equal

2.998 × 10^8 m/s

what is the frequency (s^-1) for a wave with a wavelength of 4.68 × 10^-7 m?

2.998×10^8/4.68 × 10^-7 = 6.41 × 10^14

what is the wavelenght in nannometer for a wave with frequency of 5.6 × 10^14 Hz

(2.998×10^8/5.6×10^14) = 5.35 × 10^-7 m (1nm/10^-9) = 535 nm

quantum

smallest quantity of energy that can be emitted in the form of electromagnetic radiation

energy equation

E = hv

h plancks constant

6.63 × 10^-34

what is the energy in J associated with a wave that has a wavelength of 465nm?

465nm(10^-9m/1nm)=4.65×10^-7m

(6.63×10^-34J)(2.998×10^8)/4.65×10^-7m = 4.27×10^-19

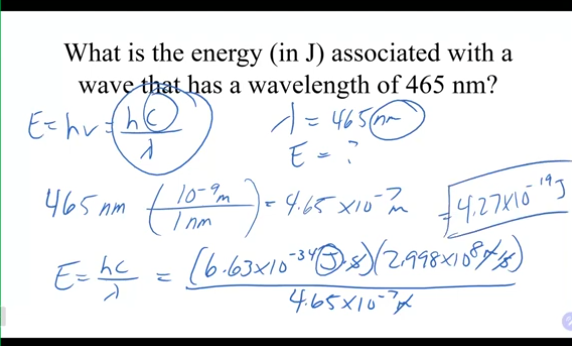
what is the energy (in J) associated with a wave that has a frequency of 2.87 × 10^14 s-1

E=hv

(6.63 × 10^-24J)(2.87×10^14 S^-1) = 1.90 × 10^-19 J

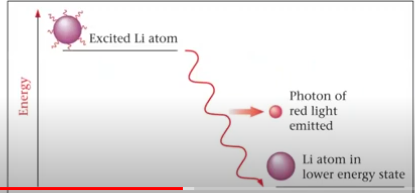
graph of an excited lithium atom emitting a photon of red light to drop a lower energy state

emission spectra

of various substances is either continuous or line spectra of radiation emitted by the substances

the emission of a substance is obtained

by energizing a sample or material either with thermal energy or with some other energy (like, high-voltage electrical discharge if substance is gaseous)

line spectra

radiation is identified by the appearance of bright lines in the spectra

niels Bohr theory

the idea of electrons moving in circular orbits

• restriction: single electron in hydrogen atom could be located only in certain orbit

• are quantized

principal quantum number

n, ground state/level

excited state or excited level

the stability of the electron diminishes for n = 2, 3 …

de Broglie

if light rays could behave like a stream of particles (photons), then perhaps particles like electrons can posses wave properties

• an electron bound to a nucleus behaves like a standing wave

Heisenberg (BREAKING BAD REFERENCE!!!!)

impossible

electron density

gives the probability that an electron will be found at a particular region in an atom

orbital or atomic orbital

a 1s orbital is merely a sphere, all s orbitals are spherical in shape but different in size

• although

p orbitals

quantum umber #2, there are three 2p orbitals

• 2px, 2py, 2pz

• the letter subscript indicate the axes along which the orbitals are oriented

d orbital

n = 3 we have 5 3d orbitals

• 3dxy, 3dyz, 3dxz, 3dxz-y2, and 3dz2

4f orbitals in terms of their boundary surfaces

• the f orbitals are a set of 7 degenerate orbitals

• the set can hold up to 14 electrons

• f orbitals available: 4f, 5f, 6f, 7f

electron configuration

tells us how electrons are distributed among the various atomic orbitals

Hydrogen, z = 1 example

1s^1

pauli exclusion principle

no two electrons in an atom can have the same four quantum numbers

• arrows have to go up and down for the electron configuration

helium, z = 2

1s²

lithium, z = 3

1s²2s^1

Beryllium, Z = 4

1s²2s²

Boron, z = 5

1s²2s²2p^1

hund’s rule

most stable arrangement of electrons in subshells is the one with the greatest number of parallel spins

Carbon, z = 6

1s²2s²2p²

Nitrogen, z = 7

1s²2s²2p³

oxygen, z = 8

1s²2s²2p^4

fluorine, z = 9

1s²2s²2p^5

Neon, z = 10

1s²2s²2p^6

argon, z = 18

1s²2s²2p^6 3s²3p^6

aufbau principle

proton are added one by one to the nucleus to build up the elements, electrons are similarly added to the atomic orbitals

K, z = 19

1s²2s²2p^6 3s²3p^6 4s^1

transition metals

either incompletely filled d subshells or readily give rise to cations that have incompletely filled d subshells

• chromium and copper are exceptions

  • 4s^1 3d^5

  • 4s^1 3d^10

lanthanide series

incompletely filled 4f subshells or readily give rise to cations that have incompletely filled 4f subshells

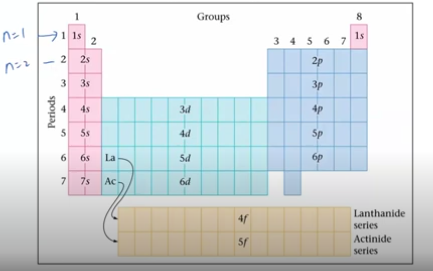
the orbitals being filled for elements in various parts of the periodic table

Na and Na+

Na = 11, 1s²2s²2p^6 3s^1

Na+ = 10, 1s²2p²2p^6

N and N³-

N = 7, 1s²2s²2p³

N³- = 10, 1s²2s²2p^6

Fe, Fe²+ and Fe³+

Fe = 26 1s²2s²2p^6 3s² 3p^6 4s² 3d^6

Fe²+ = 24 = 1s²2s²2p^6 3s² 3p^6 3d^6

Fe³+ = 23 = 1s²2s²2p^6 3s² 3p^6 3d^5

(get the S first for transition metals)

Ca²+, Br-, Mn^4+, Ni²+

Ca = 18, 1s²2s²2p^6 3s²3p^6

Br = 36, 1s²2s²2p^6 3s²3p^6 4s² 3d^10 4p^6

Mn = 21, 1s²2s²2p^6 3s²3p^6 3d³

Ni = 5, 1s²2s²2p^6 3s²3p^6 3d^8

valence electrons

electrons in the outermost (highest) principle energy level of a an atom

ionization energy

energy required to remove an electron from an individual atom in the gas phase

• M(g) → M^+ + e^-

electron affinity

energy change associated with the addition of an electron to a gaseous atom